ЭЛЕКТРОМАГНЕТИЗМ

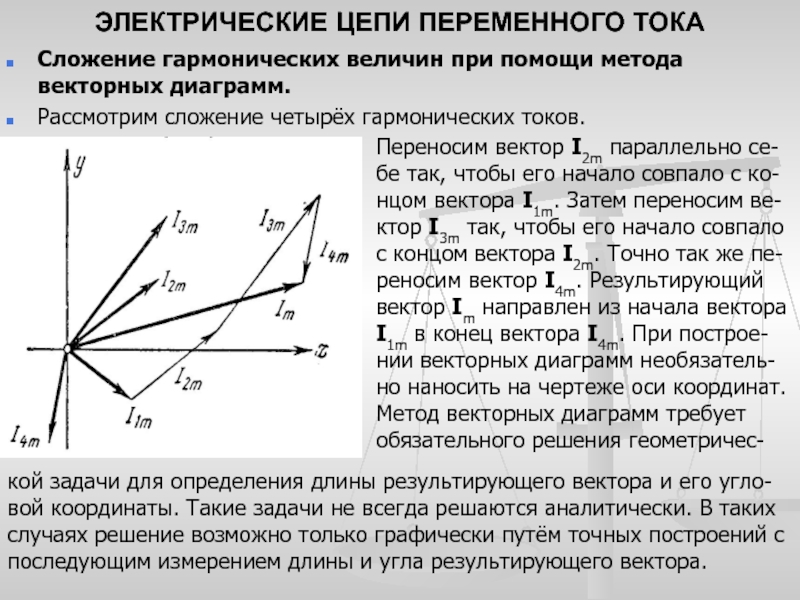
любого проводника с током возникает магнитное поле. Магнит-
ное поле вокруг

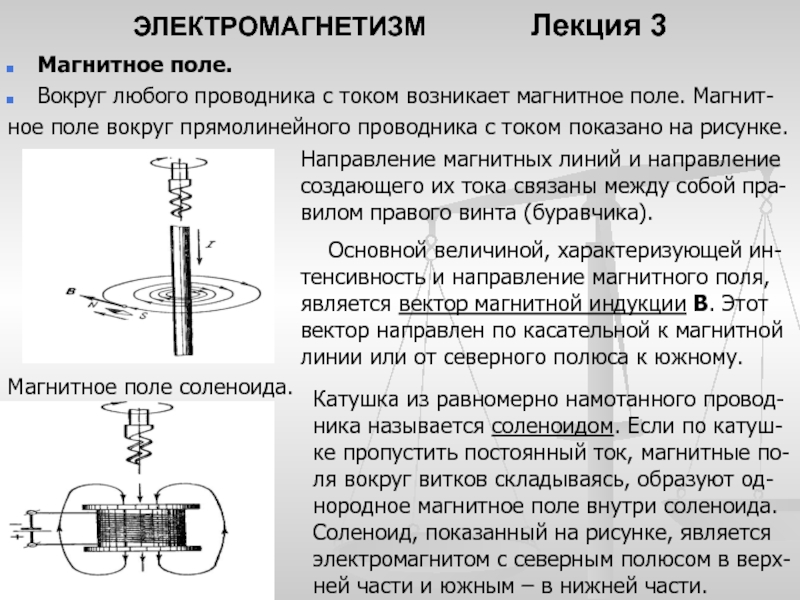
прямолинейного проводника с током показано на рисунке.

Направление магнитных линий и направление создающего их тока связаны между собой пра-вилом правого винта (буравчика).
Основной величиной, характеризующей ин-тенсивность и направление магнитного поля, является вектор магнитной индукции В. Этот вектор направлен по касательной к магнитной линии или от северного полюса к южному.

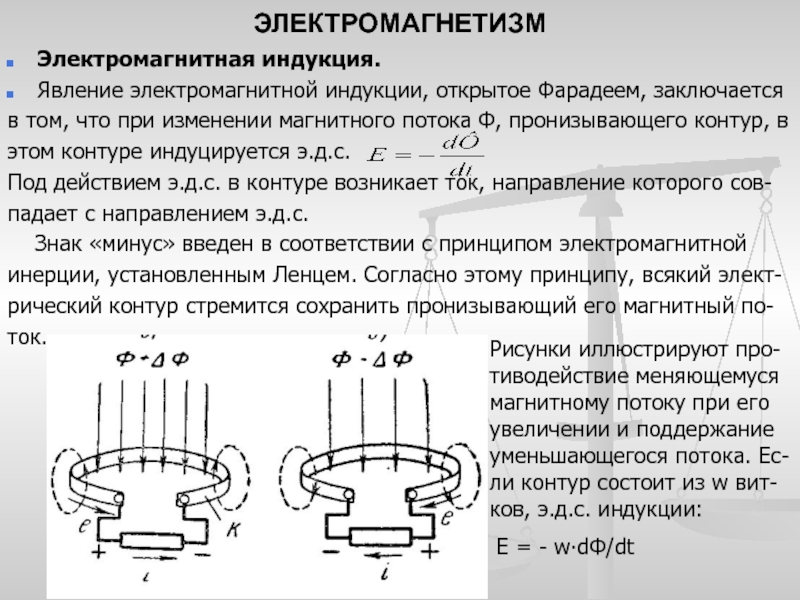
Магнитное поле соленоида.

Катушка из равномерно намотанного провод-ника называется соленоидом. Если по катуш-ке пропустить постоянный ток, магнитные по-ля вокруг витков складываясь, образуют од-нородное магнитное поле внутри соленоида. Соленоид, показанный на рисунке, является электромагнитом с северным полюсом в верх-ней части и южным – в нижней части.

Ф. Магнитный поток связан с индукцией магнитного поля
соотношением Ф

= B∙S∙cos α, где α – угол между направлением вектора
индукции и нормалью к плоскости, через которую проходит магнитный по-
ток.

В системе СИ единица измерения магнитной индукции – Тесла (Тл), а магнитного потока – Вебер (Вб).
Ещё одной характеристикой магнитного поля является напряженность магнитного поля Н. Единица измерения напряженности А/м. Вектор магнитной индукции и вектор напряженности

связаны соотношением В = μа∙Н, где μа- абсолютная магнитная проницае-мость среды: μа= μ∙μ0. Здесь μ0= 4π∙10-7 Гн/м – абсолютная магнитная про-ницаемость вакуума; μ – относительная магнитная проницаемость среды. У ферромагнитных материалов величина μ >> 1 и может достигать неско-льких тысяч или даже десятков тысяч. Поэтому при одной и той же напря-женности поля магнитный поток в ферромагнитном материале много боль-ше магнитного потока в немагнитных материалах.

неферромагнитных, по которым замыкаются линии магнитно-
го потока.
Закон

полного тока.
Математическим выражением этого закона служит следующая формула:

Здесь Н – вектор напряженности магнитного поля в данной точке простра-нства; dl – элемент длины замкнутого контура l; α – угол между направле-нием векторов H и dl; Σ Ii – алгебраическая сумма токов, пронизывающих контур l.

Ток считается положительным, если принятое направление обхода контура и направление тока связаны между со-бой правилом буравчика. Для приведе-нного примера ток I1- отрицателен, а токи I2, Ik- положительны.

виде кольца
из однородного материала. Намагничивающая обмотка расположена рав-
номерно по кольцу,

имеет w витков и обтекается током I. Магнитные линии внутри кольца представляют собой концентрические окружности.
Запишем закон полного тока, учитывая, что: 1) нап-равления векторов Н и dl совпадают, следовательно, угол α равен нулю; 2) величина Нх во всех точках кон-тура в силу симметрии одинакова; 3) сумма токов, про-низывающих контур равна Iw. Тогда Нхlx = Iw. Отсюда

где lx – длина контура; rx – радиус окружности. Магнитный поток в кольце

Произведение Iw = F получило название намагничивающей силы. Величину

l/μaS = Rm называют магнитным сопротивлением. В связи с этим получен-ную формулу принято называть законом Ома для магнитной цепи.

изменении магнитного потока Ф, пронизывающего контур, в
этом контуре индуцируется

э.д.с.
Под действием э.д.с. в контуре возникает ток, направление которого сов-
падает с направлением э.д.с.
Знак «минус» введен в соответствии с принципом электромагнитной
инерции, установленным Ленцем. Согласно этому принципу, всякий элект-
рический контур стремится сохранить пронизывающий его магнитный по-
ток.

Рисунки иллюстрируют про-тиводействие меняющемуся магнитному потоку при его увеличении и поддержание уменьшающегося потока. Ес-ли контур состоит из w вит-ков, э.д.с. индукции:
Е = - w∙dФ/dt

э.д.с. определяется по формуле:
E = B∙l∙v∙sin α, где l –

длина проводника в магнитном поле; v – скорость
его движения; α – угол между вектором скорости и вектором индукции.

Направление э.д.с. определяется правилом правой руки: правую руку располагают так, чтобы вектор индукции входил в ла-донь, а большой палец указывал направле-ние вектора скорости. Тогда четыре вытянутых пальца покажут направление э.д.с., а следовательно и направление тока.

токе.
Переменные ток, напряжение, э.д.с. – это такие величины, которые

изме-
няются во времени по периодическим законам.

На рисунке представлен график периодически изменя-ющегося переменного напряжения. Величина Т назы-вается периодом переменного напряжения. Величина, обратная периоду – частота колебаний f.

Единица измерения периода – секунда (с), частоты -

Герц (Гц). 1 Гц = с-1.
Гармонические токи и напряжения. Гармонические токи и напряжения – это такие токи и напряжения, которые изменяются во времени по гармо-ническим законам:
u(t) = Umsin(ωt + ψu) i(t) = Imsin(ωt + ψi) e(t) = Emsin(ωt + ψe)
Здесь u(t), i(t), e(t) – мгновенные напряжения, токи и э.д.с.
Um, Im, Em – их амплитудные значения. ω = 2πf– круговая (циклическая) частота. ψu, ψi, ψe – начальные фазы напряжения, тока и э.д.с.

важны не начальные фазы на-пряжений и токов, а их разность:

φ = ψu – ψi.
Наибольший интерес представляют

следующие ситуации: φ = 0, т.е. ток и напряжение совпадают по фазе;
φ = ± π/2 – сдвиг фаз между током и напряжением равен 900;
φ = ± π – ток и напряжение находятся в противофазе.
Действующее значение гармонического тока.
Действующее (эффективное) значение характеризует тепловое действие переменного тока. Действующее значение периодического тока численно равно такому постоянному току, который за время, равное периоду пере-менного тока, выделяет такое же количество тепла, что и переменный ток.
Действующее значение

необходимо выполнять действия
над гармоническими функциями по правилам тригонометрии, что вызыва-
ет

затруднения. Метод векторных диаграмм упрощает подобные преобра-
зования.
В этом методе гармоническая величина представляется вектором, длина
которого равна амплитудному значению тока (напряжения, э.д.с.), угол
между направлением вектора и осью абсцисс равен начальному фазовому
углу. При этом за положительное значение принимается угол отсчитывае-
мый против часовой стрелки от оси абсцисс.

Такое изображение гармонической величины векто-ром соответствует моменту времени t = 0. В любой другой момент времени угол будет равен ω∙t + φ. То есть вектор вращается с частотой ω. Обычно пре-образования осуществляют с гармоническими величинами имеющими одинаковую частоту ω. Поэтому при отсчёте угла можно не учитывать переменную ω∙t , одинаковую для всех величин и считать вектор неподвижным с углом, равным начальному фазовому углу.

диаграмм.
Рассмотрим сложение 2-х гармонических э.д.с.:
e1 = E1msin(ωt+ψ1); e2 =

E2msin(ωt+ψ2).
Представим векторы E1m и E2m на одном графике.

Результирующий вектор суммы двух векторов является диагональю параллелограмма. Его длина Еm, угол к оси х равен φ. Следовательно, определив эти величины из решения геометри-ческой задачи, запишем суммарную э.д.с. в гармоническом виде: e = Emsin(ωt+φ).
Метод векторных диаграмм позволяет осуществлять сложение любого числа гармонических величин. Для этого необходимо знать правило сложения векторов – начало второго вектора совмещают с концом пер-вого, затем начало третьего вектора совмещают с

концом второго и т.д. Результирующий вектор направлен из начала перво-го в конец третьего. При вычитании векторов используют то же правило, только вектор, имеющий знак минус проводят в противоположном направ-лении.

диаграмм.
Рассмотрим сложение четырёх гармонических токов.
Переносим вектор I2m параллельно се-бе так,

чтобы его начало совпало с ко-нцом вектора I1m. Затем переносим ве-ктор I3m так, чтобы его начало совпало с концом вектора I2m. Точно так же пе-реносим вектор I4m. Результирующий вектор Im направлен из начала вектора I1m в конец вектора I4m. При построе-нии векторных диаграмм необязатель-но наносить на чертеже оси координат. Метод векторных диаграмм требует обязательного решения геометричес-

кой задачи для определения длины результирующего вектора и его угло-вой координаты. Такие задачи не всегда решаются аналитически. В таких случаях решение возможно только графически путём точных построений с последующим измерением длины и угла результирующего вектора.

векторных диаграмм невозможно осуществлять опе-
рации умножения и деления гармонических величин.

Метод комплексных
амплитуд – более универсальный. Он позволяет производить любые алге-
браические преобразования гармонических величин. Метод основан на
представлении гармонической величины комплексным числом.
Обычные числа, которые используются в вычислениях, называются дей-
ствительными числами. Любое действительное число можно представить
на числовой оси, которая называется осью действительных чисел.

Ось действительных чисел

Таким образом, любое действительное число мо-жет быть представлено точкой на прямой (число-вой оси). И наоборот – любую точку на прямой

можно представить действительным числом.
Если же нужно задать координаты любой точки на плоскости, не лежа-щей на оси действительных чисел, необходимы уже 2 числа, одно из кото-рых является проекцией на ось х (ось действительных чисел), а другое яв-ляется проекцией на ось у. Эту ось называют осью мнимых чисел.
Мнимое число j = √-1.

на плоскости заданы её проекциями на ось действительных чисел (2)

и на ось мнимых чисел (j). Эти координа-ты представляют комплексным числом
Å = 2 + j. В общем случае комплексное число представляют выражением Å = a + j∙b. Для точ-ки А на плоскости a = 2; b = 1. Такая форма пре-дставления комплексного числа называется ал-гебраической. Если в точку А провести из нача-ла координат вектор, то координаты этого век-тора можно задать этим же комплексным чис-

лом. Так как гармоническую величину можно представить вектором, зна-чит эту величину можно представить комплексным числом, у которого действительная часть – проекция вектора на ось Х, а мнимая часть – прое-кция на ось У.
Другой формой записи комплексного числа является показательная фо-рма. В показательной форме комплексное число имеет вид Å = А∙еjφ.
Здесь А – модуль комплексного числа; φ – аргумент комплексного числа.

Аргумент комплексного числа
Для представления гармони-
ческой величины комплексным числом вначале записывают

её в показа-
тельной форме. В качестве модуля берут обычно действующее значение, а
аргументом является начальная фаза.
Например, необходимо записать ток i = 10∙sin(ωt + 600) в виде компле-
ксного действующего значения. В показательной форме: İ = 5√2∙еj∙60.

Для записи алгебраической формы а и b находим из прямоугольного треугольника: а = 5√2∙cos 600 = 2,5√2 b = 5√2∙sin 600 = 2,5√6. Алгебраическая форма записи
İ =2,5√2 + j∙ 2,5√6
Для обратного преобразования необходимо записать комплексное число в показательной форме, а затем представить его в гармоническом виде. Например:
İ = 50√2∙е-j∙30 i = 100∙sin(ωt – 300)

комплексными числами.
Операции сложения:

Для сложения (вычитания)
двух комплексных чисел необходимо сложить (вычесть)

отдельно их дейс-твительные и мнимые части.
Операции умножения:
Для умножения комплексных чисел необходимо перемножить их модули и сложить аргументы.
Операции деления:

Для деления комплексных чисел необходимо разделить их модули и вы-честь аргументы.
Перемножение комплексно сопряженных чисел:

цепи с активным сопротивлением R, к зажимам которо-го подключен источник

синусоидаль-ного напряжения U. В рассматривае-мой цепи напряжение источника:
u = Umsin ωt. Для произвольного мо-мента времени справедлив закон Ома

Следовательно, в цепи с активным сопротив-лением ток и напряжение совпадают по фазе.

Мощность в цепи переменного тока.
p = u∙i = UmImsin2ωt

Несмотря на то, что ток и напряжение за период колебаний меняют знак, знак мощности всегда ос-тается положительным. Это означает, что в актив-ной нагрузке происходит процесс необратимого преобразования электрической энергии в другой вид. Такую мощность называют активной.

с индуктивностью L под действием приложенного пе-ременного напряжения u протекает

синусоидальный ток i = Imsin ωt. Этот ток вызывает в катушке э.д.с. самоиндукции

По второму закону Кирхгофа – eL= u. Следовательно

Полученное выражение показывает, что в цепи с индуктивностью ток от-стает от напряжения на 900. Кроме того Um= ω∙L∙Im. Или

Разделив обе части выражения на √2, получим такое же соотношение для действующих значений тока и напря-жения. Выражение в знаменателе имеет смысл индуктив-ного сопротивления Xl = ω∙L. В отличие от активного со-противления R индуктивное сопротивление зависит от частоты. Чем выше частота, тем больше XL.

цепи с индуктивностью:
Мгновенная мощность изменяется по закону синуса с удвоенной

частотой.

В течение первой четверти периода ток и на-пряжение положительны, следовательно по-ложительна и мощность. В этот промежуток времени катушка потребляет энергию из сети. В следующую четверть периода ток положи-телен, а напряжение отрицательно. Следова-тельно мощность отрицательна. Отрицатель-

ное значение мощности означает, что энергия, запасённая в магнитном поле катушки возвращается в сеть. В третьей четверти периода и ток и напряжение отрицательны, а мощность положительна. Т.е. энергия опять потребляется, но при противоположном направлении тока. В последней четверти периода напряжение положительно, ток отрицателен и мощность тоже отрицательна. Значит энергия опять возвращается в сеть. Мощность, которая не потребляется, а циркулирует от источника к нагрузке и обрат-но, называется реактивной мощностью. Q = I2xL

напряжение на клеммах меняется по закону
u = Umsin ωt.

Учитывая, что q = C∙u

Ток опережает по фазе напряжение на 900. Это связано с тем, что при полном заряде конденсатора ток равен нулю, а напряжение при этом мак-симально. Из полученного выражения следует, что Im = CωUm. Записывая это выражение в общепринятой форме закона Ома, получим:

Разделив обе части на √2, аналогичное выражение получим и для действующих значений тока и напряжения:

Следовательно, выражение в знаменателе пред-ставляет собой емкостное сопротивление:
Емкостное сопротивление уменьшается
с увеличением емкости и с ростом частоты пере-менного тока.

в цепи с емкостью:
Из формулы видно, что мгновенная мощ-ность меняется

по закону синуса с удво-енной частотой. В первой четверти пери-ода ток и напряжение положительны, по-этому положительна и мощность. Эта мо-щность потребляется от сети и расходует-ся на зарядку конденсатора. Во второй четверти периода напряжение положи-тельно, а ток отрицателен. В итоге мощ-ность – отрицательна, т.е. конденсатор разряжается и отдает энергию источнику.

В следующей четверти периода и ток и напряжение отрицательны, а мощ-ность положительна. Конденсатор заряжается обратной полярностью, пот-ребляя энергию от источника. В последней четверти периода мощность от-рицательна. Т.е. конденсатор отдает энергию источнику. Как и в случае с индуктивной нагрузкой – это реактивная мощность. Q = I2xC

состоящую из индуктивности и активного сопротивле-
ния.
Напряжение на зажимах та-кой

цепи складывается из па-дения напряжения на актив-ном сопротивлении UR и на индуктивности UL: U = UR+ UL
Произведя сложение векто-ров, получим вектор U, пове-

рнутый на угол φ относительно вектора тока I.
Таким образом, в цепи с индуктивностью и активным сопротивлением ток отстаёт по фазе от напряжения на угол меньший 900. Величину сдвига фаз можно найти из треугольника напряжений:
Так как в последовательной цепи течёт один и
тот же ток, то аналогичное выражение можно получить из треугольника сопротивлений:

содержащей емкость и ак-тивное сопротивление напряже-ние на зажимах складывается из

суммы падений напряжений на емкости и на активном сопротив-лении U = UR + UC.

Производя сложение векторов UR и UC, получаем вектор U, повернутый на угол – φ относительно вектора тока I. Таким образом, в цепи с емкостью и активным сопротивлением напряжение отстаёт от тока на угол меньший 900. Угол сдвига фаз можно определить из треугольника напряжений или из треугольника сопротивлений.

Гипотенуза в треугольнике сопротивлений представляет собой модуль полного сопротивления Z.
Полное сопротивление цепи с ре-
активным сопротивлением явля-
ется величиной комплексной: