Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Элементы матричной алгебры
Содержание
- 1. Элементы матричной алгебры
- 2. Слайд 2
- 3. Слайд 3
- 4. Слайд 4
- 5. Слайд 5
- 6. Слайд 6
- 7. Слайд 7
- 8. Слайд 8
- 9. 1.2. Операции с матрицами и их свойстваРавенство матриц.
- 10. Согласно (1.8)
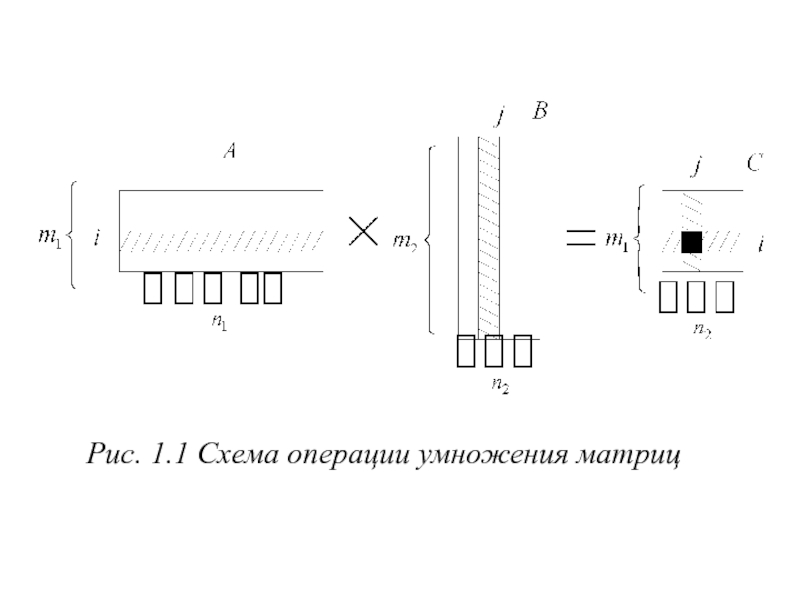
- 11. Рис. 1.1 Схема операции умножения матриц
- 12. Пример 1.4. Найти произведение
- 13. Пример 1.5. Найти произведение квадратнойматрицы и вектор–столбца.
- 14. Произведение двух матриц
- 15. 1.3. Определитель матрицы.. (1.10)
- 16. Пример 1.6. Вычислить определитель 3-го порядка
- 17. Линейная зависимость и
- 18. Свойства определителей 1. Равноправие строк и столбцов 2. Если
- 19. 4. Определитель с двумя одинаковыми столбцами(строками) равен
- 20. 1.4. Алгебраические дополнения и минорыРассмотрим определитель D
- 21. Алгебраическое дополнение На рис.1.1
- 22. Пример 1.9. Проверить,
- 23. 1.5. Обратная матрица Обратной
- 24. Обращение матрицы можно осуществить по следующему правилу.
- 25. Пример 1.10. Произвести обращение матрицы и доказать, что она обратная. Решение
- 26. Доказательство: Если A-1
- 27. 1.6. Системы линейных алгебраических уравнений
- 28. Слайд 28
- 29. Примером системы, обладающей единственным решением является, например:
- 30. Пример 1.11. Решить
- 31. Решение. Применим в качестве базисных неизвестных,что позволяет
- 32. Скачать презентанцию
Слайды и текст этой презентации
Слайд 14 Произведение двух матриц не обладает
переместительным свойством:
,
в
чем можно убедиться на примере:
,
, тогда
и
.
Слайд 17 Линейная зависимость и линейная комбинация
элементов матрицы
Запишем два столбца:
,
(1.14)где λ – действительное число.
Указанные столбцы A1 и A2 являются линейно
зависимыми, вследствие их связи через коэффициент
пропорциональности λ.
Слайд 18Свойства определителей
1. Равноправие строк и столбцов
2. Если все элементы какого-либо
столбца (строки)
определителя равны нулю, то сам определитель равен
нулю
3. При
перестановке местами двух любыхстолбцов определителя его знак изменяется
на противоположный; абсолютная величина
не меняется
Слайд 19 4. Определитель с двумя одинаковыми столбцами
(строками) равен нулю:
5. Если
какой-либо столбец определителя
является линейной комбинацией других его столбцов,
то определитель равен
нулю 6. Определитель не изменится, если к любому его
столбцу прибавить произвольную линейную
комбинацию других столбцов
7. Общий множитель некоторого столбца (строки)
определителя можно вынести за знак этого определителя
Слайд 201.4. Алгебраические дополнения и миноры
Рассмотрим определитель D 3-го порядка (n
= 3):
Выделим в нем, например, элемент aij = a13.
.
(1.24)
Слайд 21Алгебраическое дополнение
На рис.1.1 показаны знаки сомножителя
(-1)i+j
для определителя 3-го порядка
Рис. 1.2
Слайд 22 Пример 1.9. Проверить, что для треугольных
матриц определитель равен произведению
диагональных элементов и det A =
det AT:,
.
Слайд 231.5. Обратная матрица
Обратной матрицей A-1 по
отношению к исходной A
называется такая матрица, которая, будучи умноженной
на исходную слева или справа, даст единичную матрицу:
. (1.28)
Слайд 24 Обращение матрицы можно осуществить
по следующему правилу.
1. Вычислить определитель исходной матрицы
Δ = det A.
3. Транспонировать матрицу алгебраических дополнений, что дает присоединенную матрицу
по отношению к исходной матрице A.
4. Каждый элемент присоединенной матрицы
разделить на определитель исходной матрицы Δ.
Слайд 271.6. Системы линейных алгебраических уравнений
Предположим, что
задана система m линейных
уравнений относительно n неизвестных x1, x2,
…, xn. В развернутой форме её можно записать так:
Слайд 31Решение. Применим в качестве базисных неизвестных
,
что позволяет (1.40) представить в
следующем виде:
,
,
. (1.41)
Общее решение:
,
,
,
в котором базисные переменные линейно выражаются
через свободную переменную x4.