Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Элементы теории множеств
Содержание
- 1. Элементы теории множеств
- 2. Понятие множества Множество - это совокупность определенных различаемых
- 3. Обычно множества обозначают большими буквами: A,B,X N
- 4. Множества могут быть конечными, бесконечными и пустыми.
- 5. Способы задания множествСуществуют три способа задания множеств:1)
- 6. Заданы два множества:
- 7. Множество А называют подмножеством множества В (обозначается
- 8. Множества А и В равны (А=В) тогда
- 9. Множество А называется собственным подмножеством множества В,
- 10. Операции над множествамиОбъединением (суммой) множеств А и
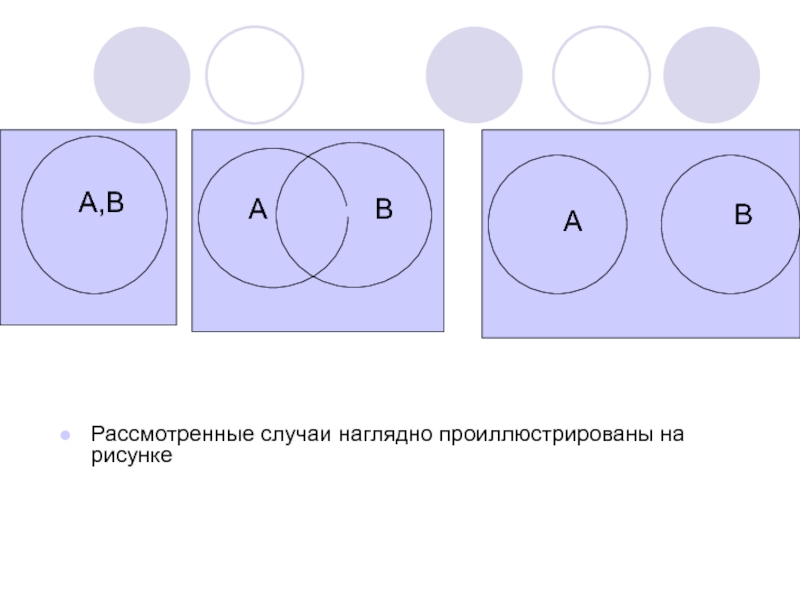
- 11. Рассмотренные случаи наглядно проиллюстрированы на рисункеА,ВАВАВ
- 12. Пересечением множеств А и В называется новое
- 13. Примеры:1)А={1,2,3}, B= {1,2,3}, тогда А∩В= {1,2,3}.2)А={1,2,3}, B={2,3,4,5,6}, тогда А∩В={2,3}3) A={1,2,3}, B={4,6,8}, тогда А∩В=∅
- 14. Разностью множеств А и В называется множество
- 15. Даны два множества: А={1,2,3,b,c,d},В={2,b,d,3}.Тогда:A∪B={1,2,3,b,c,d}B подмножество АА\В={1,c}A∩B={2,3,b,d}
- 16. Свойства:1. Коммутативность объединения А∪B=B ∪ A2. Коммутативность
- 17. Декартовое (прямое) произведение А и В -
- 18. A×B ≠ В × А, кроме если
- 19. Скачать презентанцию
Понятие множества Множество - это совокупность определенных различаемых объектов, причем таких, что для каждого можно установить, принадлежит этот объект данному множеству или нет
Слайды и текст этой презентации
Слайд 2Понятие множества
Множество - это совокупность определенных различаемых объектов, причем таких,
Слайд 3Обычно множества обозначают большими буквами: A,B,X N ,…, а их
элементы – соответствующими маленькими буквами: a,b,x,n…
В частности, приняты следующие
обозначения: ℕ – множество натуральных чисел;
ℤ – множество целых чисел;
ℚ – множество рациональных чисел;
ℝ – множество действительных чисел (числовая прямая).
C – множество комплексных чисел. И верно следующее:
N⊂ Z⊂ Q ⊂ R ⊂ C
Принадлежность элемента m множеству M обозначается так: m∈M
Слайд 4Множества могут быть конечными, бесконечными и пустыми.
Множество, содержащее конечное
число элементов, называется конечным.
Если множество не содержит ни одного
элемента, то оно называется пустым и обозначается Ø.Например:
множество студентов 1курса - конечное множество;
множество звезд во Вселенной - бесконечное множество;
множество студентов вашего курса, хорошо знающих три иностранных языка (японский, китайский и французский), видимо, пустое множество.
Слайд 5Способы задания множеств
Существуют три способа задания множеств:
1) описание множества
Примеры: Y={yΙ1≤y
≤10} –множество значений у из отрезка [1;10]
X={xIx>2} – множество всех
чисел х, больших 2.2) перечисление множества
Примеры:
А={а,б,в}- три начальные буквы русского алфавита
N={1,2,3…}-натуральные числа
3)графическое задание множеств происходит с помощью диаграмм Эйлера-Венна
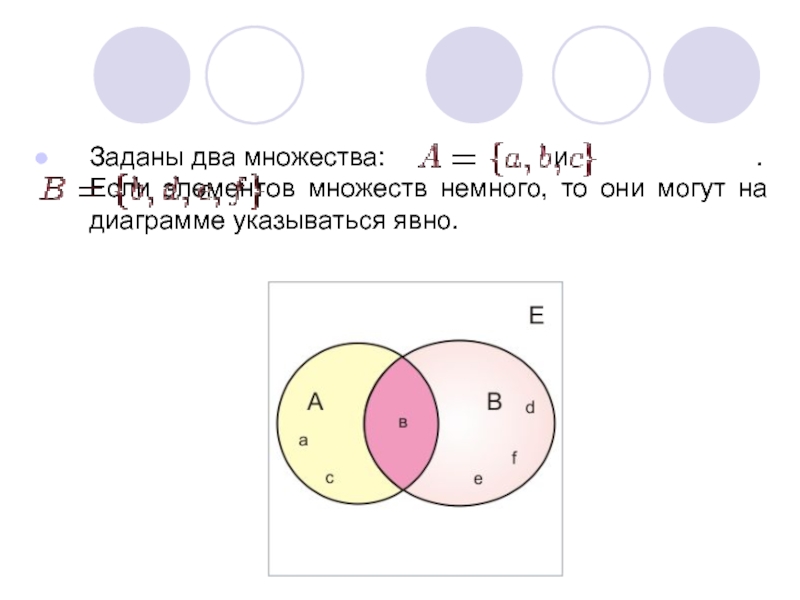
Слайд 6Заданы два множества:
и .Если элементов множеств немного, то они могут на
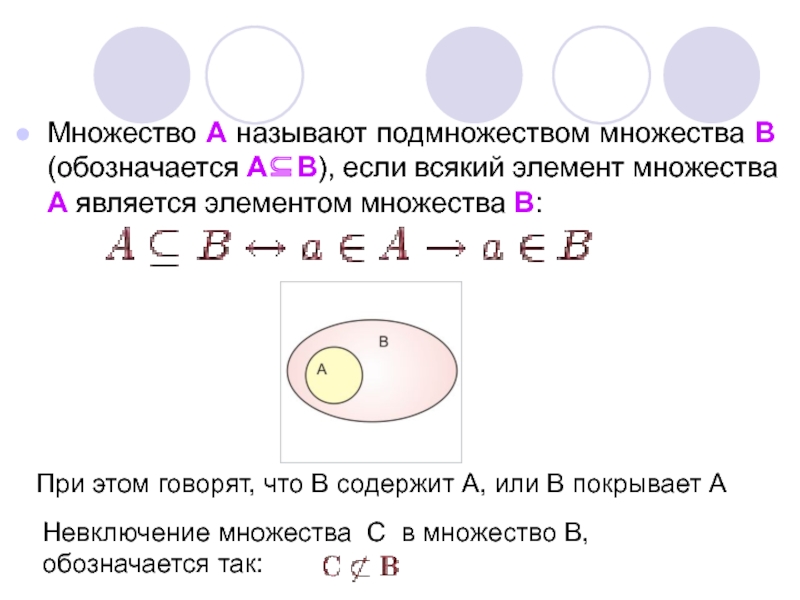
диаграмме указываться явно.Слайд 7Множество А называют подмножеством множества В (обозначается А⊆В), если всякий
элемент множества А является элементом множества В:
При этом говорят,
что В содержит А, или В покрывает АНевключение множества С в множество В, обозначается так:
Слайд 8Множества А и В равны (А=В) тогда и только тогда,
когда , А⊆В и В⊆А , т. е. элементы множеств
А и В совпадают.Пример: А={1,2,3}, B={3,2,1}, C={1,2,3,3}- равны. Множество С – это множество А, только в нем элемент 3 записан дважды.
Пример: А={1,2}, B={1,2,3}- НЕ РАВНЫ
Семейством множеств называется множество, элементы которого сами являются множествами.
Пример: А={{Ø},{1,2},{3,4,5}}- семейство, состоящее из трех множеств.
Каждое непустое множество А≠ Ø имеет по крайней мере два различных подмножества: само множество А и Ø.
Слайд 9Множество А называется собственным подмножеством множества В, если А⊆В, а
В⊄А. Обозначается так: А⊂В.
Например,
Принято считать, что пустое множество является
подмножеством любого множества.Мощностью конечного множества М называется число его элементов. Обозначается |M|
Например, |B|=6. |A|=3.
Слайд 10Операции над множествами
Объединением (суммой) множеств А и В (обозначается А∪В)
называется множество С тех элементов, каждый из которых принадлежит хотя
бы одному из множеств А или В. Возможны три случая:1) А=В;
2) множества имеют общие элементы;
3) множества не имеют общих элементов.
Примеры:
1)А={1,2,3}, B= {1,2,3}, тогда А∪В= {1,2,3}.
2)А={1,2,3}, B={2,3,4,5,6}, тогда А∪В={1,2,3,4,5,6}
3) A={1,2,3}, B={4,6,8}, тогда А∪В={1,2,3,4,6,8}
Слайд 12Пересечением множеств А и В называется новое множество С, которое
состоит только из элементов одновременно принадлежащих, множествам А и В
Обозначение С=А ∩В
Возможны три случая:
1) А=В
2) множества имеют общие элементы
3) множества не имеют общих элементов.
Слайд 13Примеры:
1)А={1,2,3}, B= {1,2,3}, тогда А∩В= {1,2,3}.
2)А={1,2,3}, B={2,3,4,5,6}, тогда А∩В={2,3}
3) A={1,2,3},
B={4,6,8}, тогда А∩В=∅
Слайд 14Разностью множеств А и В называется множество С, состоящее из
элементов принадлежащих только множеству А и не принадлежащих В.
Обозначение: С=А\В
Слайд 15Даны два множества:
А={1,2,3,b,c,d},В={2,b,d,3}.
Тогда:
A∪B={1,2,3,b,c,d}
B подмножество А
А\В={1,c}
A∩B={2,3,b,d}
Слайд 16Свойства:
1. Коммутативность объединения А∪B=B ∪ A
2. Коммутативность пересечения А ∩
В=В ∩ А
3. Сочетательный закон A ∪(B ∪ C)=B ∪(A
∪ C)4. То же и для пересечения.
5. Распределительный относительно пересечения
А ∩ (В ∪ C) = A ∩ В ∪ A ∩ С
6. Распределительный относительно объединения
А ∪(B ∩ С) = (А ∪ B) ∩ (A ∪ C)
7. Закон поглощения А ∪(A∩В)=А
8. Закон поглощения А ∩(А ∪ B)=A
9. А ∪ A=А
10. A ∩ А=A
Слайд 17Декартовое (прямое) произведение А и В - это новое множество
С, состоящее из упорядоченных пар, в которых первый элемент пары
берется из множества А, а второй из В.А={1,2,3}
В={4,5}
С=А×В = {(1,4);(1,5);(2,4);(2,5);(3,4);(3,5)}
Мощность декартова произведения равна произведению мощностей множеств А и В:
|А × В|=|А |∙ | В |
Слайд 18A×B ≠ В × А, кроме если А=В (в этом
случае равенство выполняется)
Дано:
Координатная числовая ось Х.х∈ (-∞,+ ∞). Координатная числовая
ось Y.у∈ (-∞,+ ∞). D=Х × Y
Декартовое произведение двух осей - точка на плоскости.
Рассмотрим декартовое произведение, которое обладает свойством коммутативности. А={Иванов, Петров}
В={высокий, худой, сильный}
А × В= {Иванов высокий, Иванов худой, Иванов сильный, Петров высокий, Петров худой, Петров сильный}




![Элементы теории множеств Способы задания множествСуществуют три способа задания множеств:1) описание множестваПримеры: Y={yΙ1≤y ≤10} Способы задания множествСуществуют три способа задания множеств:1) описание множестваПримеры: Y={yΙ1≤y ≤10} –множество значений у из отрезка [1;10]X={xIx>2}](/img/thumbs/5e512cd8dec959bb49541c4c2cf8094c-800x.jpg)