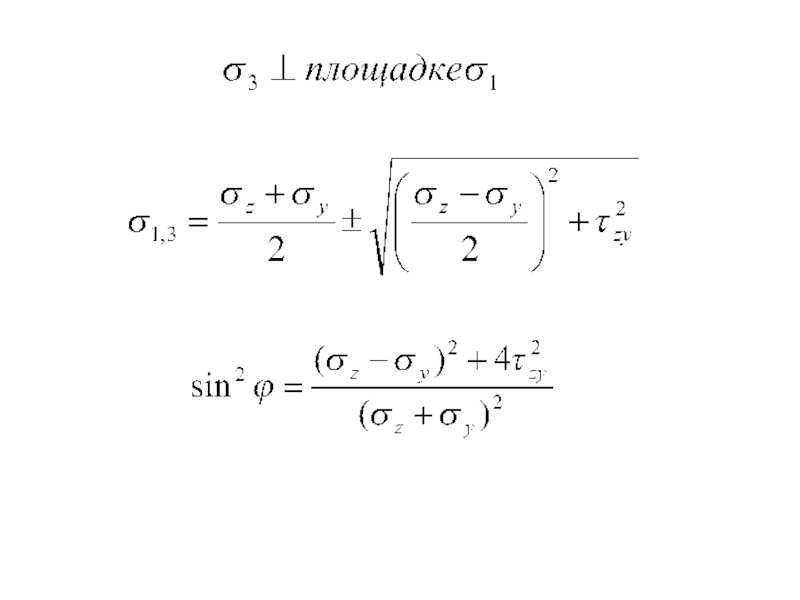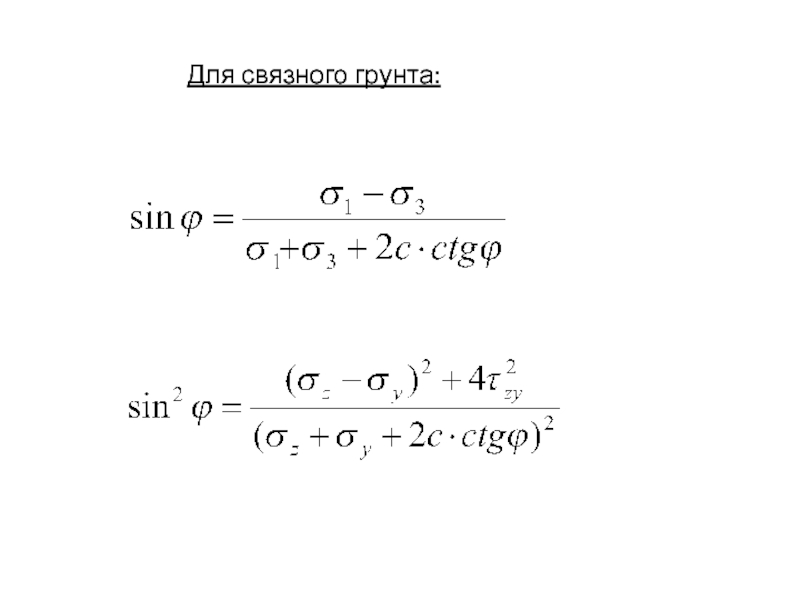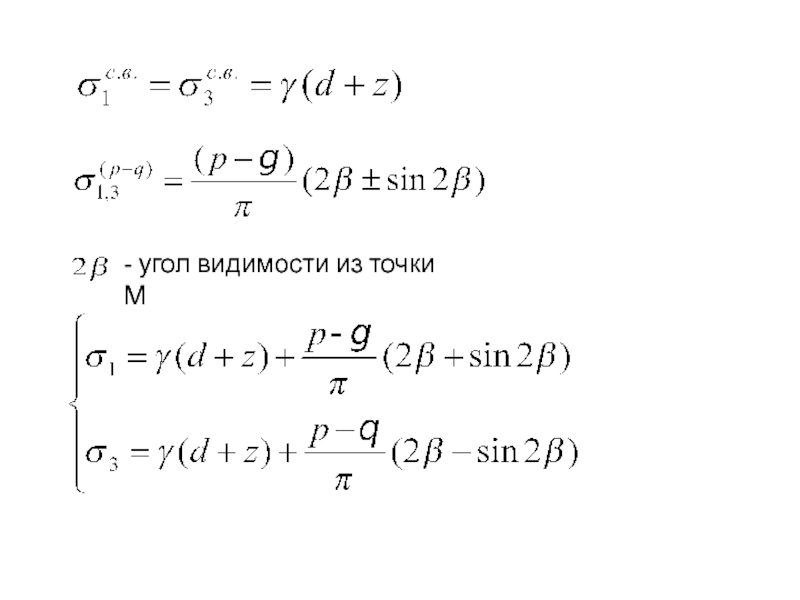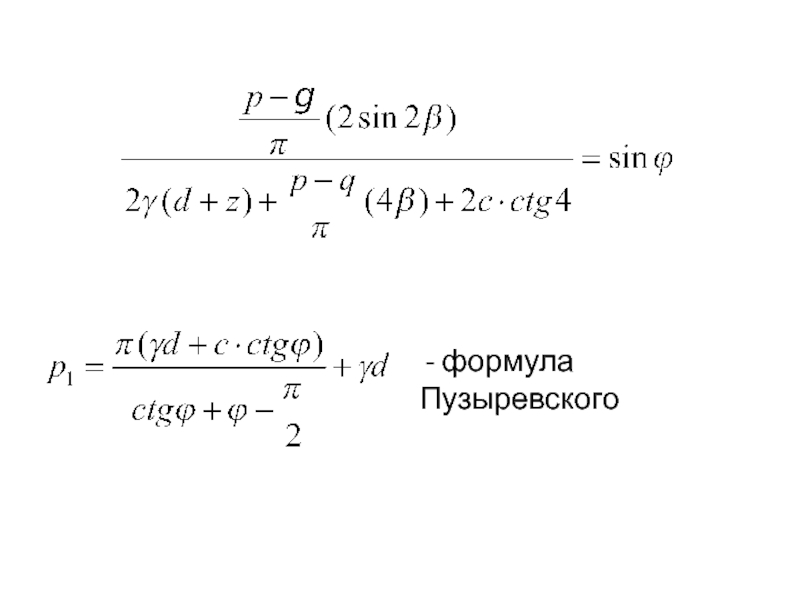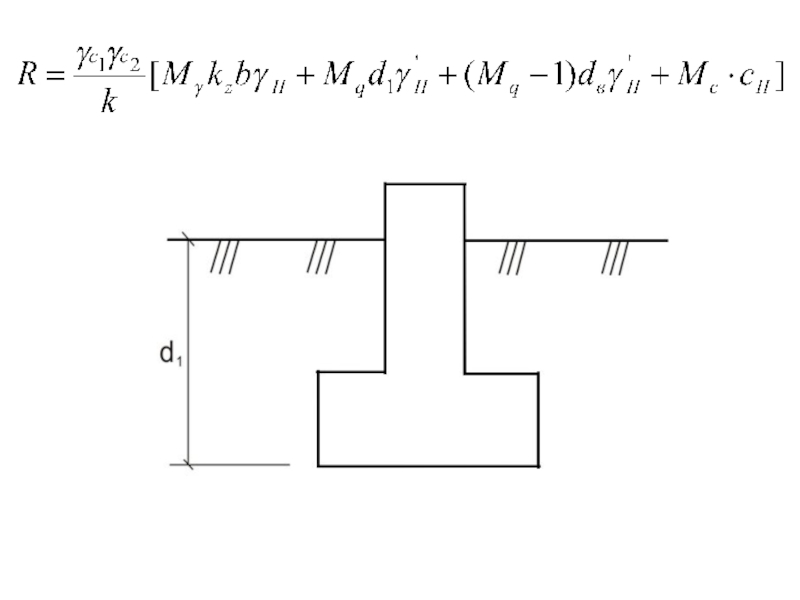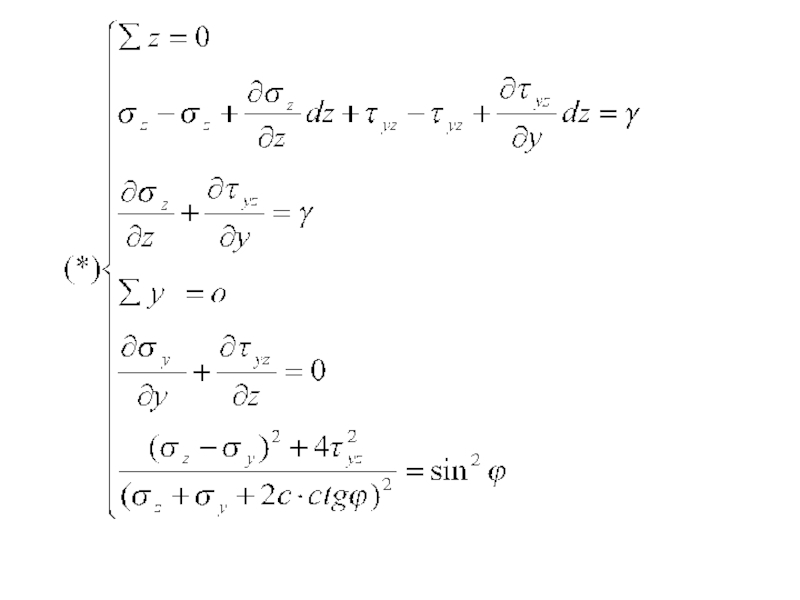Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Фазы напряженного состояния грунта
Содержание
- 1. Фазы напряженного состояния грунта
- 2. Предельное напряженное
- 3. Слайд 3
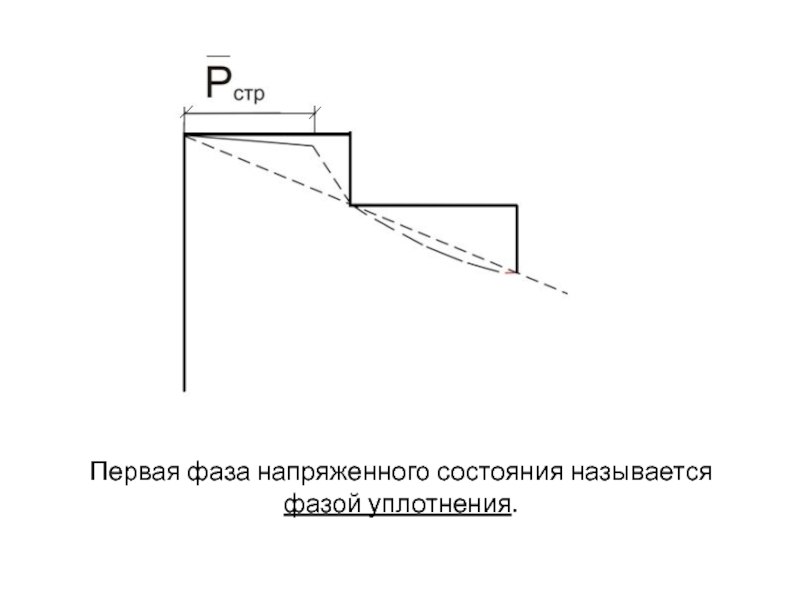
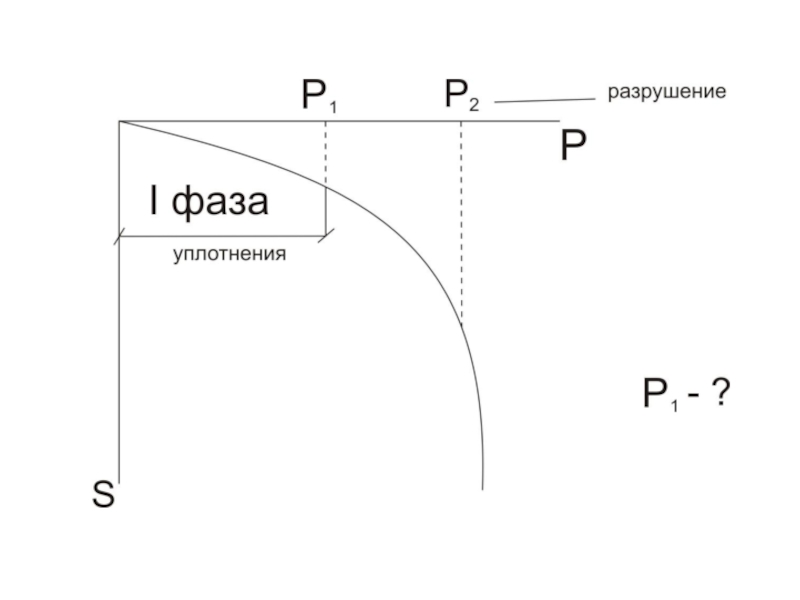
- 4. Первая фаза напряженного состояния называется фазой уплотнения.
- 5. Конец фазы уплотнения и начало образования зон
- 6. Слайд 6
- 7. В конце фазы уплотнения (начале фазы сдвигов)
- 8. Ядро полностью сформировывается при достижении грунтом его
- 9. При дальнейшем увеличении нагрузки наступает вторая фаза - фаза сдвигов.
- 10. 2ая критическая нагрузка
- 11. Предельное напряженное состояние в точке для сыпучих
- 12. Рис. 1
- 13. При изменении угла α, величины составляющих
- 14. Если - величина постоянная, то в предельном
- 15. для связных грунтов
- 16. С другой стороны согласно рис.1,
- 17. Слайд 17
- 18. Рассмотрим
- 19. (формула 2)- условие предельного равновесия для сыпучих
- 20. Условию предельного равновесия можно придать другой вид,
- 21. Слайд 21
- 22. Для связного грунта:
- 23. Расчет оснований по несущей способности.(по I группе
- 24. Расчет по I группе предельных состояний обязателен
- 25. 4. При возведении фундамента на скальном основании.5. В соответствии с требованиями к железобетонным и бетонным конструкциям.
- 26. Критические нагрузки на грунт Расчетное сопротивление грунта основания
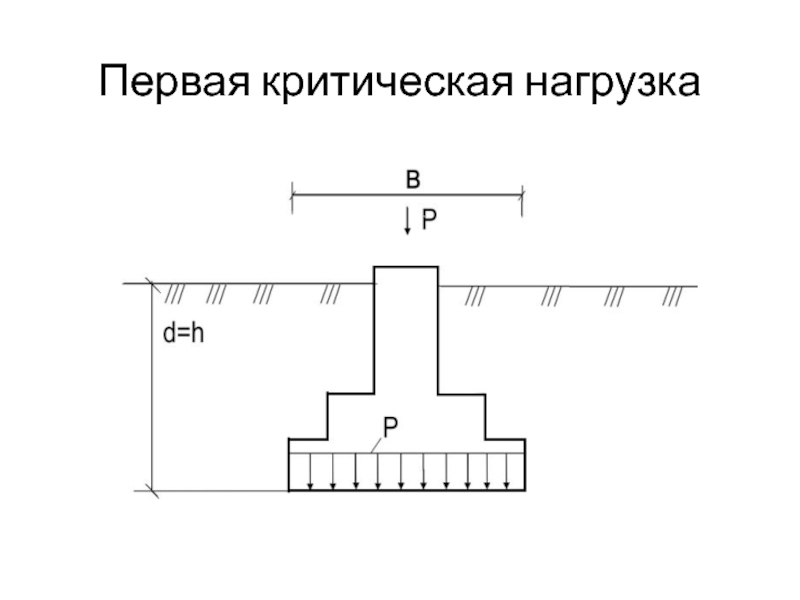
- 27. Первая критическая нагрузка
- 28. Слайд 28
- 29. Р – равномерно распределенная нагрузкаg – боковая
- 30. - уравнение предельного равновесияДля зоны сдвигов в каждой точке выполняется условие предельного равновесия.
- 31. - угол видимости из точки М
- 32. - формула Пузыревского
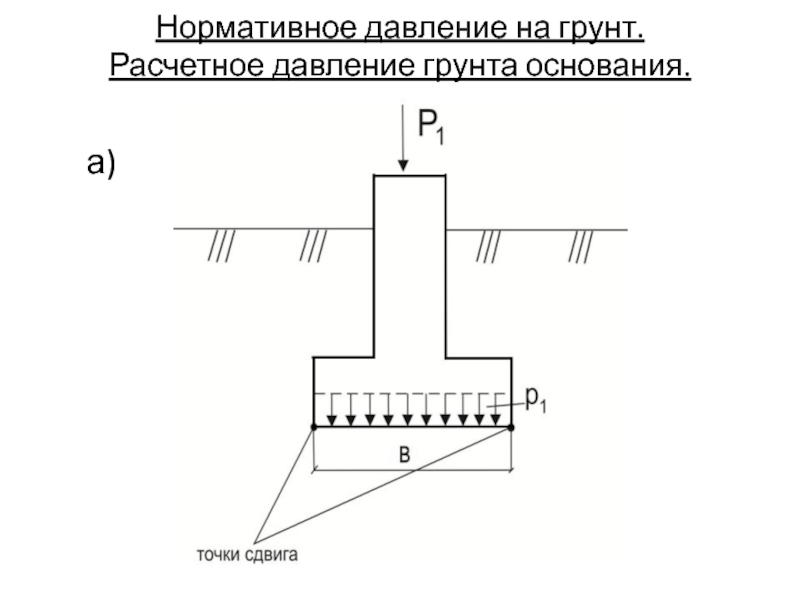
- 33. Нормативное давление на грунт. Расчетное давление грунта основания. а)
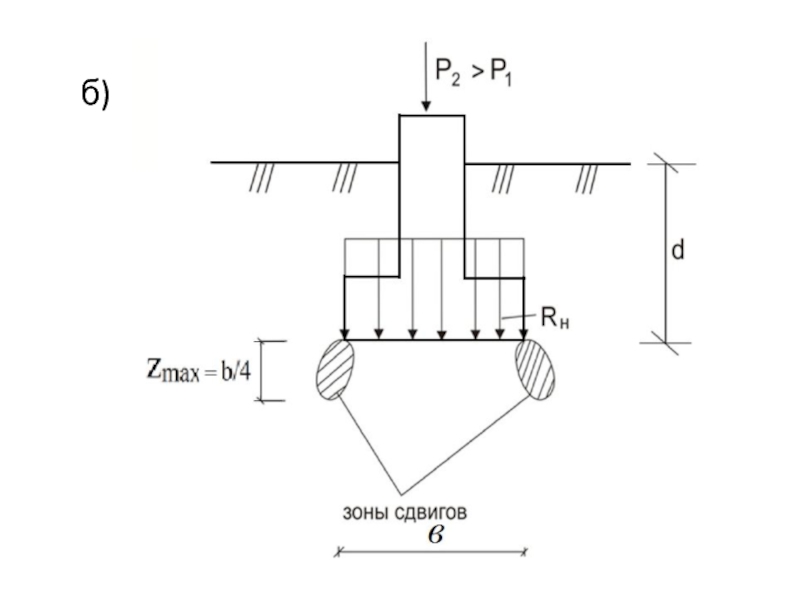
- 34. б)
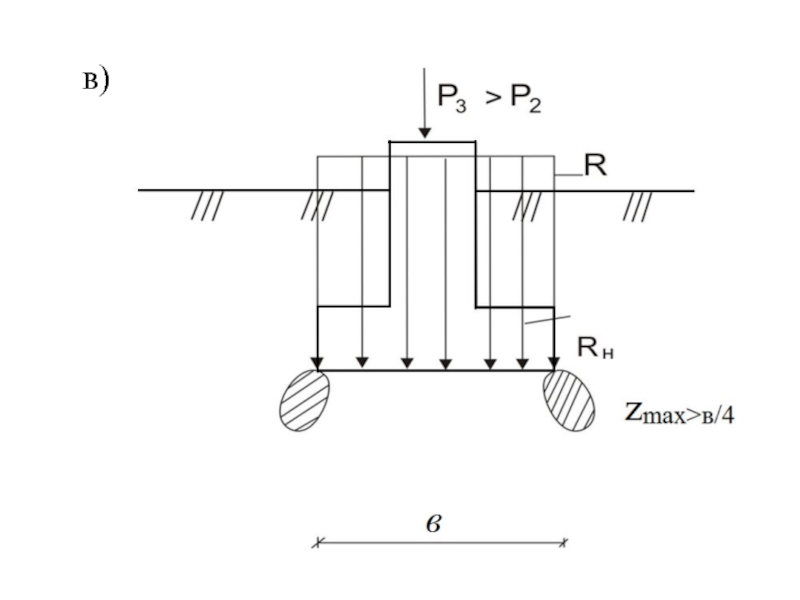
- 35. в)
- 36. m1 – коэффициент, зависящий от вида грунтов
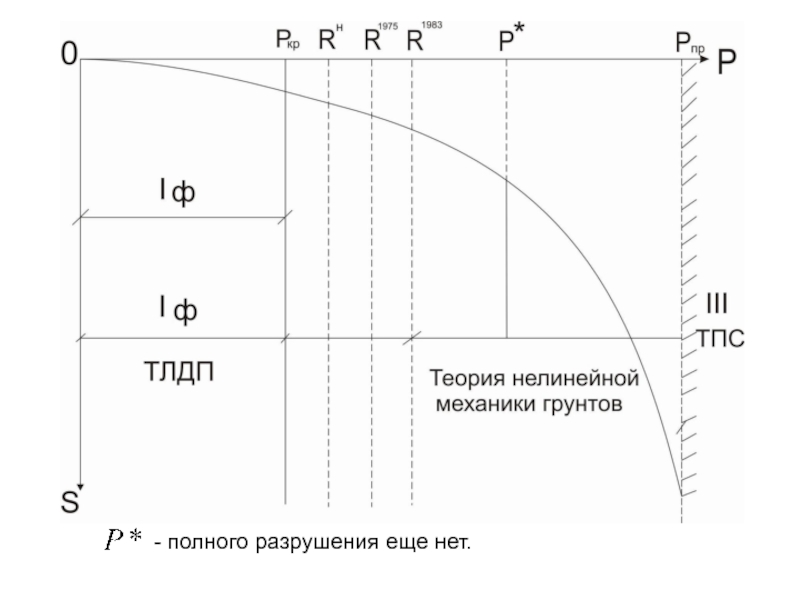
- 37. - полного разрушения еще нет.
- 38. Слайд 38
- 39. Слайд 39
- 40. Коэффициенты условий работы: γc1 - табличный коэффициент,
- 41. γII - удельный вес грунта под подошвой
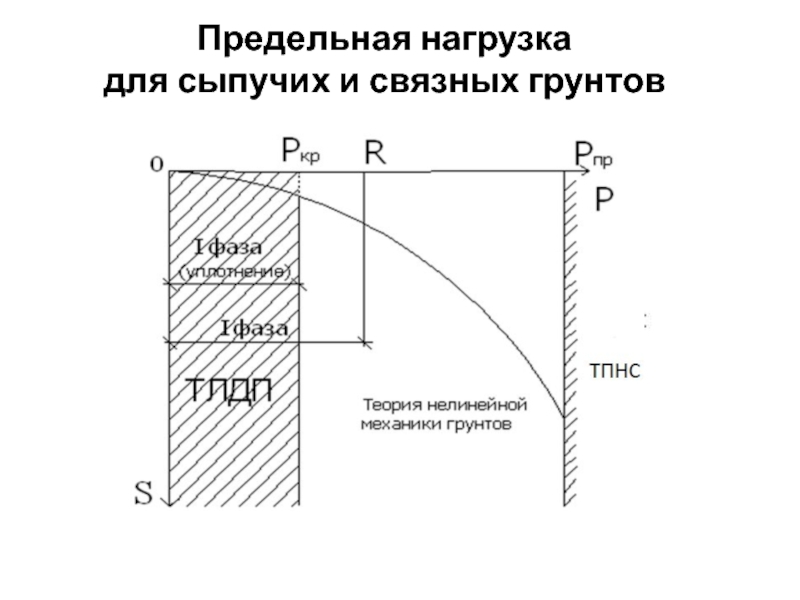
- 42. Предельная нагрузка для сыпучих и связных грунтов
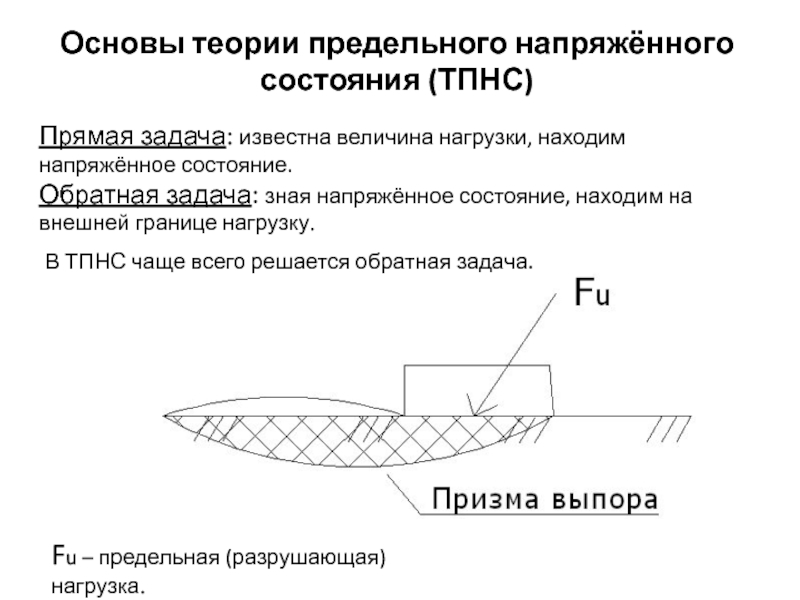
- 43. Основы теории предельного напряжённого состояния (ТПНС)Прямая задача:
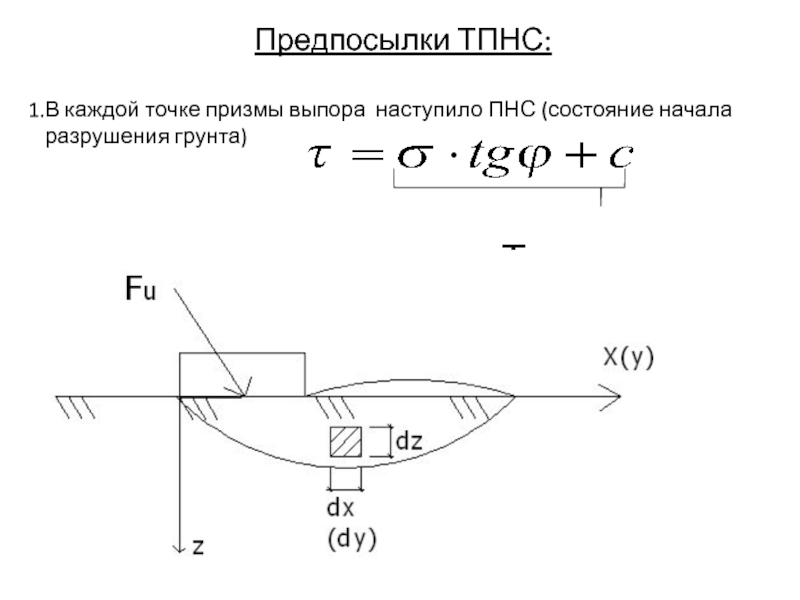
- 44. Предпосылки ТПНС:В каждой точке призмы выпора наступило
- 45. 2. Грунт в пределах призмы выпора однороден.3.
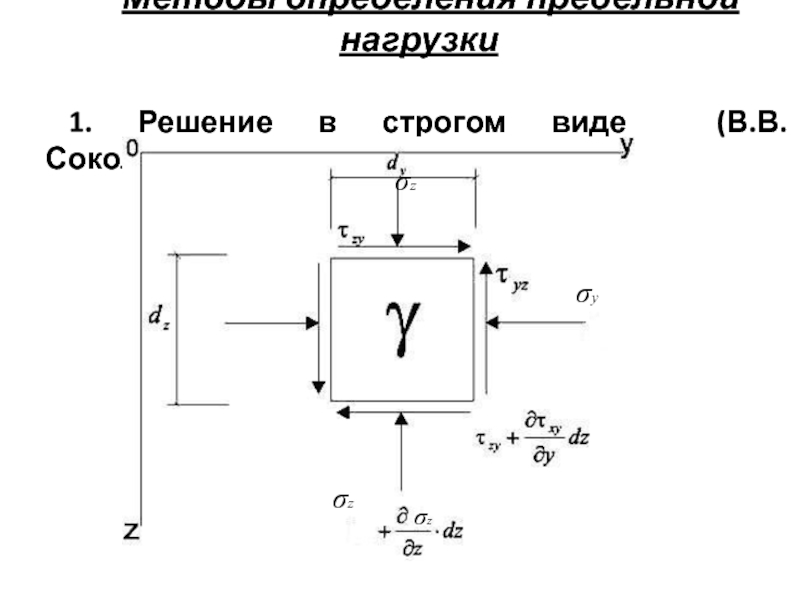
- 46. Методы определения предельной нагрузки1. Решение в строгом виде (В.В. Соколовского)σyσzσzσz
- 47. Слайд 47
- 48. В результате строгого интегрирования системы (*) мы
- 49. Равнодействующая приложена справа
- 50. F ≤ Fu - расчет оснований по
- 51. Приближенный метод Соколовского(равнодействующая)1-ая зона призмы выпирания.Сетка скольжения.2-ая зона призмы выпирания .Веер, логарифмическая спираль.3-я зона призмы выпирания.
- 52. Уплотнённое ядроγ = 0 Метод В.Г.Березанцева
- 53. Решение для осесимметричной нагрузки В.Г.Березанцева При полосовой нагрузке:, При круглом фундаменте:
- 54. где N с соответствующими индексами – табличные
- 55. Для сыпучих грунтов (В.Г.Березанцев):Плоская задача - Пространственная
- 56. Метод ПрандтляПрандтль рассматривает невесомую среду γ = 0.
- 57. Формула Прандтля:q – интенсивность нагрузки собственного веса фундамента;с и ϕ- прочностные характеристики грунта под подошвой фундамента.
- 58. Формула Березанцева: - табличные коэффициенты, зависящие
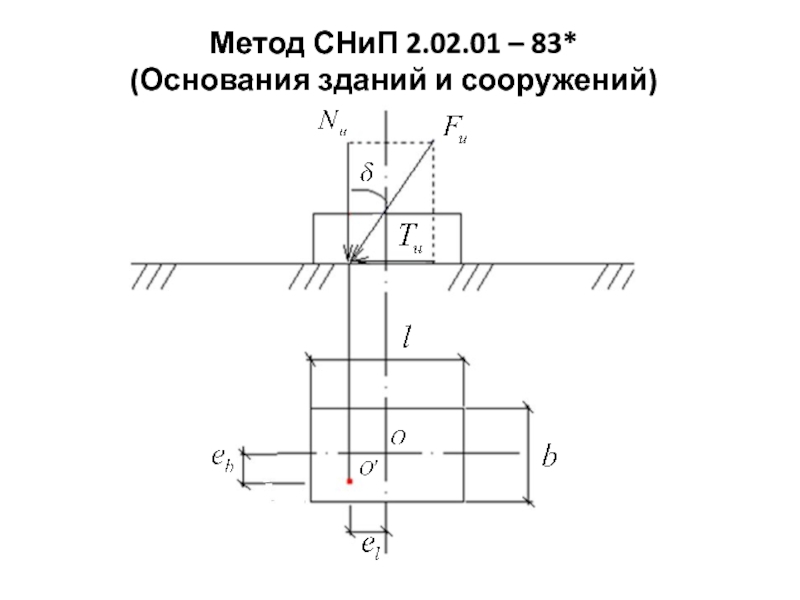
- 59. Метод СНиП 2.02.01 – 83* (Основания зданий и сооружений)
- 60. Слайд 60
- 61. Fu - предельное (разрушающее) значение равнодействующей всех
- 62. табличные коэффициенты, зависящие от φ, δ→ f
- 63. Скачать презентанцию
Слайды и текст этой презентации
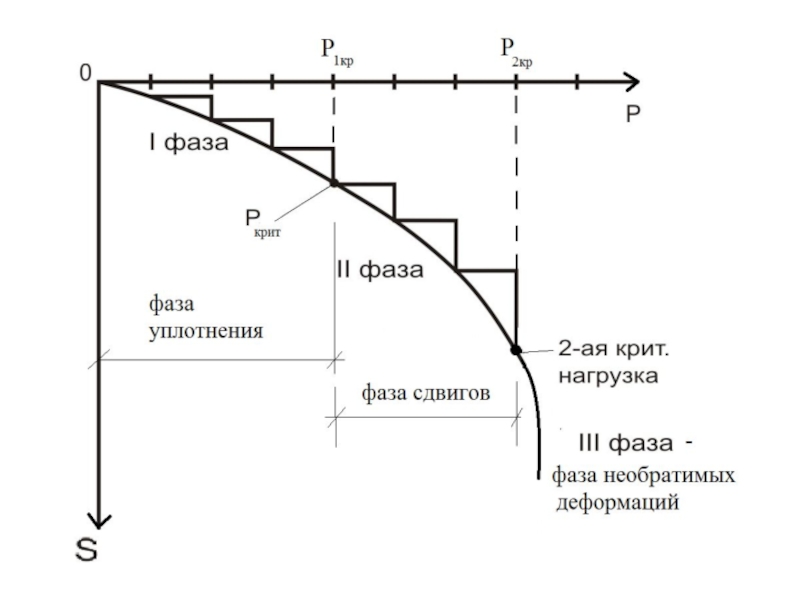
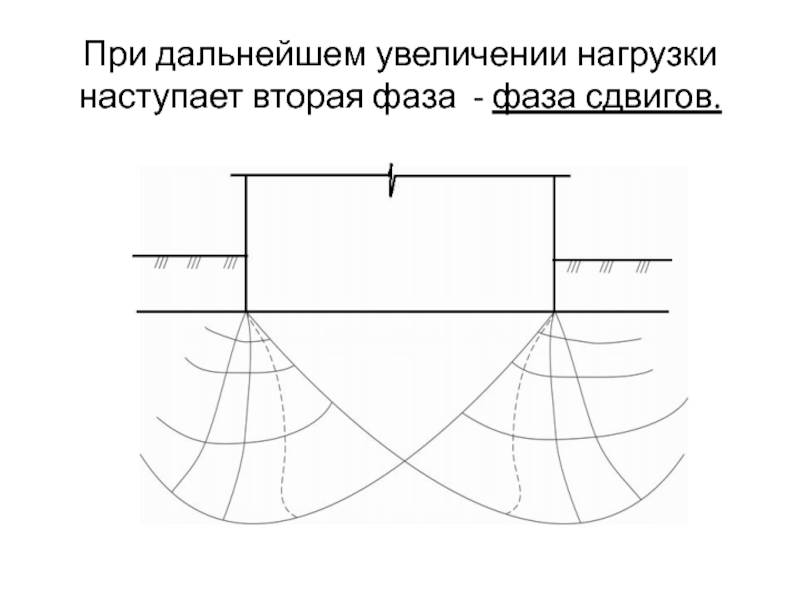
Слайд 5 Конец фазы уплотнения и начало образования зон сдвигов соответствует начальной
критической нагрузке (или 1-ой критической нагрузке). 1ая критическая нагрузка –
нагрузка, соответствующая началу возникновения в грунте зон сдвигов и окончанию фазы уплотнения, когда под краем нагрузки между касательными и нормальным напряжениями возникают соотношения, приводящие грунт (сначала у ребер подошвы фундаментов) в предельное напряженное состояние.Слайд 7В конце фазы уплотнения (начале фазы сдвигов) непосредственно под штампом
начинает формироваться жесткое ядро ограниченных смещений частиц, которое в дальнейшем
расклинивает и разжимает грунт в стороны, обуславливая значительные осадки штампа.Слайд 8Ядро полностью сформировывается при достижении грунтом его максимальной несущей способности,
после чего остается неизменным, но возникают добавочные пластические области ядра,
которые меняя свое положение, какбы выискивают более слабые места в массиве грунта, в то время как жесткое ядро, оставаясь без изменения, внедряется в массив грунта.При возникающем при этом предельным напряженным состоянии грунта преобладают боковые смещения частиц и формируются непрерывные поверхности скольжения, в результате чего толща грунта теряет устойчивость.
Слайд 10 2ая критическая нагрузка – нагрузка, при
которой под нагруженной поверхностью сформировываются сплошные области предельного равновесия, грунт
приходит в неустойчивое состояние и полностью исчерпывается его несущая способность. 3 фаза –фаза недопустимых деформаций основания (пластическое или прогрессирующее течение, выпирание, просадка и др. недопустимых деформаций основания).Слайд 11Предельное напряженное состояние в точке для сыпучих и связных грунтов
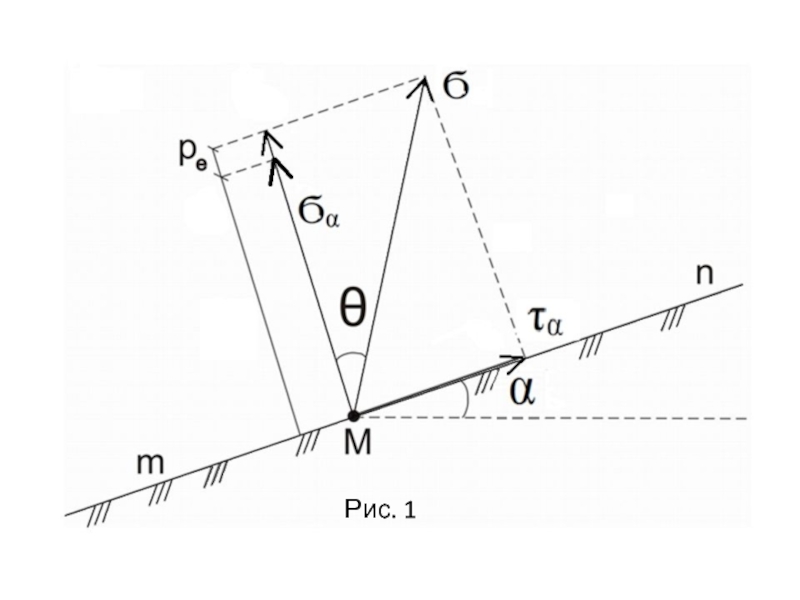
При действии на поверхность грунта нагрузки в любой точке М
для любой площадки mn, проведенной через эту точку под углом α, возникнут нормальные и касательные напряжения.К нормальным напряжениям следует отнести и силы связности, суммарно оцениваемые давлением связности ре .
Тогда на площадку mn будут действовать нормальные напряжения σα+ре и касательные τα
Слайд 13 При изменении угла α, величины составляющих напряжений также будут меняться
и, если касательные напряжения достигнут определенной доли от нормальных, то,
как показывают опыты на сдвиг, произойдет скольжение одной части грунта относительно другой. Таким образом, условием предельного равновесия грунта в данной точке будет: или
(1)
(1) Условие Кулона
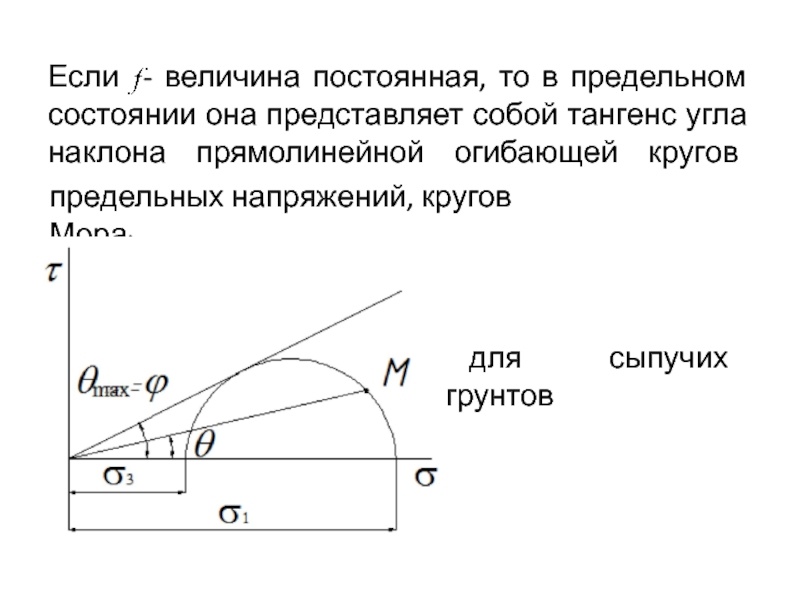
Слайд 14Если - величина постоянная, то в предельном состоянии она представляет
собой тангенс угла наклона прямолинейной огибающей кругов
предельных напряжений,
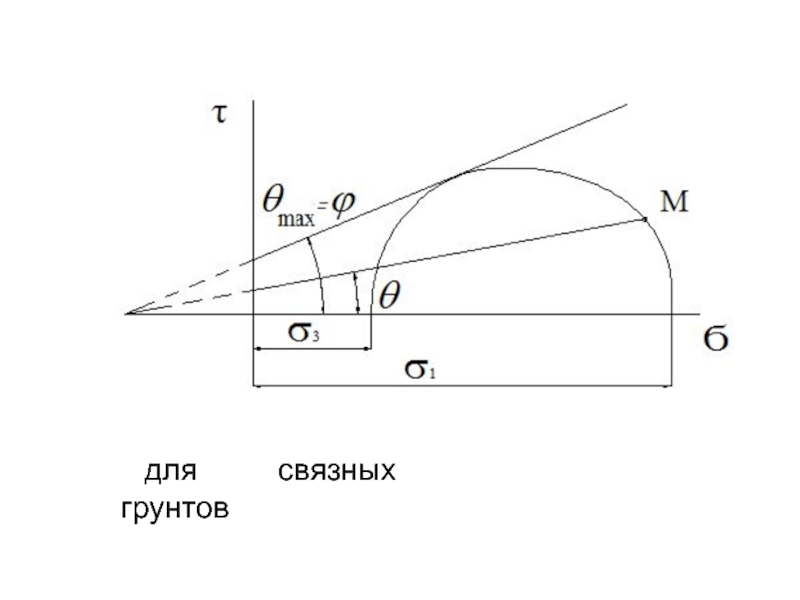
кругов Мора:для сыпучих грунтов
Слайд 16
С другой стороны согласно рис.1,
Это отношение равно тангенсу угла отклонения θ, т.е. угла,
на который отклоняется полное напряжение для площадки τ от нормали к этой площадке. Т.к. через заданную точку можно провести множество площадок, то, очевидно, необходимо отыскать самую невыгодную площадку, для которой будет существовать максимальный угол отклонения θmax.Слайд 18
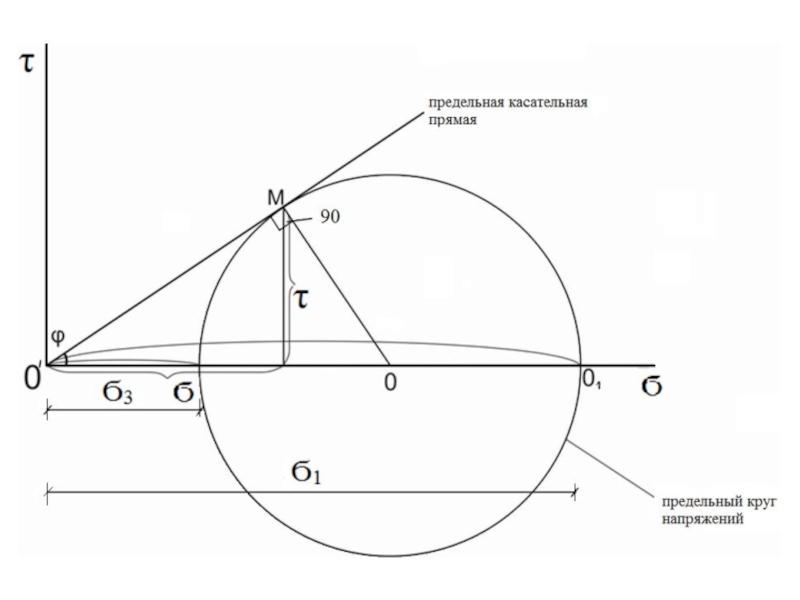
Рассмотрим
:
и
- главные напряжения;
- угол внутреннего трения грунта.
на их разности как на d
строится круг Мора
ОМ = ОО1= r
(2)
Слайд 19
(формула 2)- условие предельного равновесия для сыпучих грунтов.
или
Это выражение широко
используются в теории давления грунтов на ограждение. Знак «-» соответствует
активному давлению, а «+» пассивному сопротивлению сыпучих грунтов.Слайд 20
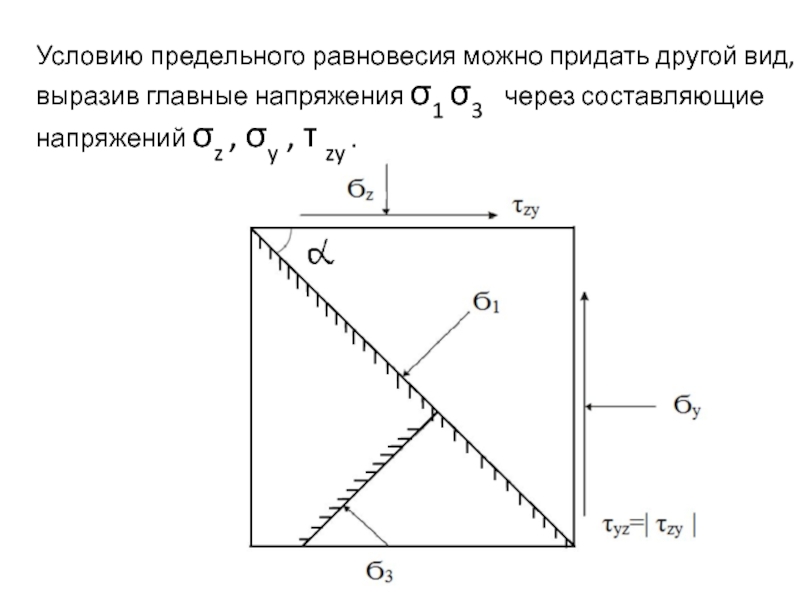
Условию предельного равновесия можно придать другой вид, выразив главные напряжения
σ1 σ3 через составляющие напряжений σz , σy ,
τ zy .Слайд 23Расчет оснований по несущей способности.
(по I группе предельных состояний)
F≤γc*Fu/γn
,где F - расчетная нагрузка
Fu- сила предельного состояния
γc – коэффициент надежности, принимаемый в зависимости от класса зданий
γn- коэффициент условия работы, принимаемый в зависимости от вида грунта.
Слайд 24
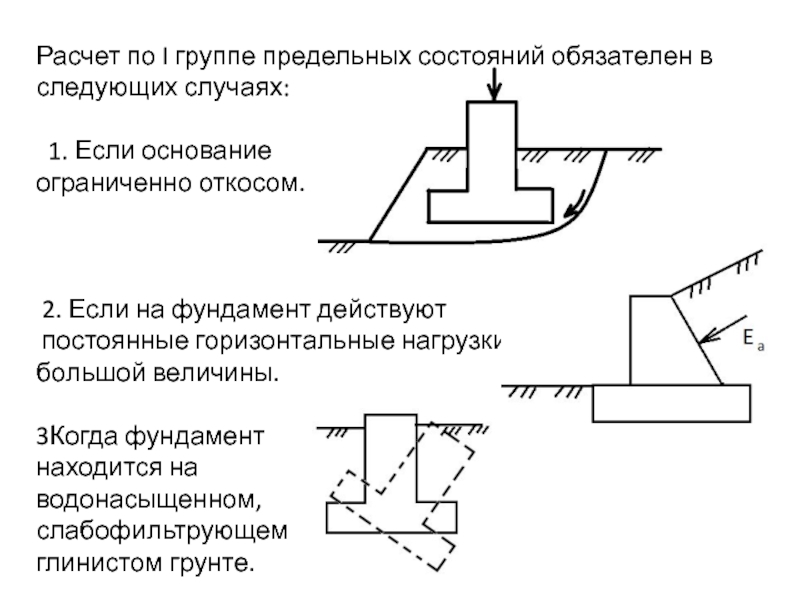
Расчет по I группе предельных состояний обязателен в следующих случаях:
1. Если основание
ограниченно откосом.
2. Если
на фундамент действуютпостоянные горизонтальные нагрузки
большой величины.
3Когда фундамент
находится на
водонасыщенном,
слабофильтрующем
глинистом грунте.
Слайд 254. При возведении фундамента на скальном основании.
5. В соответствии с
требованиями к железобетонным и бетонным конструкциям.
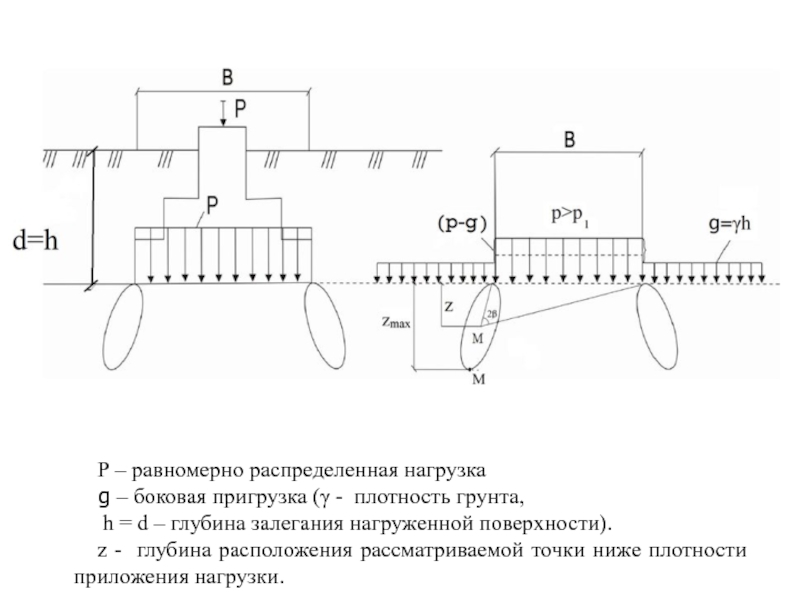
Слайд 29Р – равномерно распределенная нагрузка
g – боковая пригрузка (γ -
плотность грунта,
h = d – глубина залегания нагруженной поверхности).
z
- глубина расположения рассматриваемой точки ниже плотности приложения нагрузки.
Слайд 30
- уравнение предельного равновесия
Для зоны сдвигов в каждой точке
выполняется условие предельного равновесия.
Слайд 36m1 – коэффициент, зависящий от вида грунтов основания;
m2 - коэффициент,
зависящий от вида грунтов и конструктивной
схемы здания (сооружения),kн – коэффициент надежности;
R
При наблюдениях увеличили давление за счет коэффициентов
В 1962 г. вышел первый СНиП.
СНиП 1962 г. -
Слайд 40Коэффициенты условий работы:
γc1 - табличный коэффициент, зависящий от вида
и состояния грунтов основания;
γc2 – коэффициент, зависящий от вида, состояния
грунтов и конструктивной схемы здания (сооружения);k - коэффициент надежности, зависящий от способа определения прочностных характеристик грунтов;
Mγ, Mq, Mc - табличные коэффициенты, зависящие от угла внутреннего трения основания
kz – коэффициент, зависящий от ширины подошвы фундамента;
Слайд 41γII - удельный вес грунта под подошвой фундамента;
γ’II - удельный
вес грунта выше подошвы фундамента;
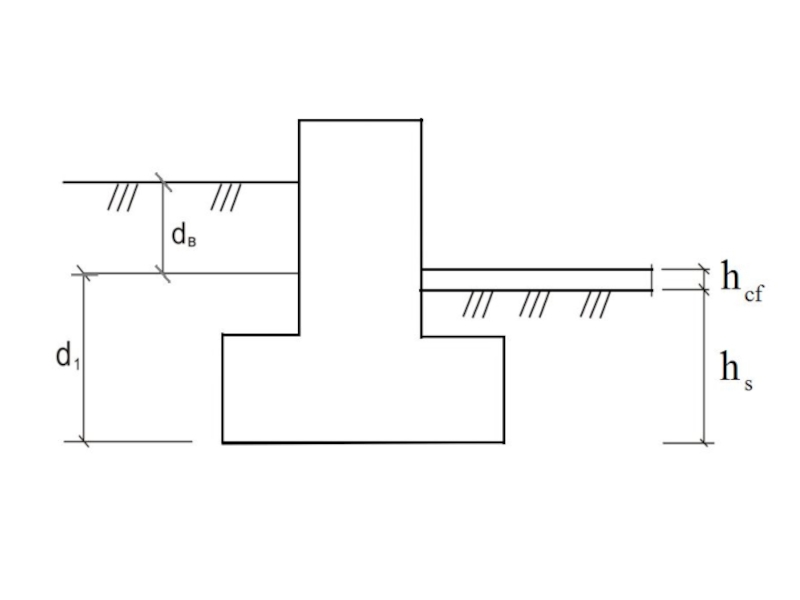
d1 – для здания без подвала
– это глубина заложения фундамента (расстояние от планировочной отметки до подошвы).Для здания с подвалом:
hs - толщина слоя грунта выше уровня подошвы фундамента со стороны подвала (пригрузка грунта);
hcf - толщина конструкции пола подвала;
γcf - удельный вес материала пола подвала
CII - удельное сцепление грунта, расположенного под подошвой фундамента.
Слайд 43
Основы теории предельного напряжённого состояния (ТПНС)
Прямая задача: известна величина нагрузки,
находим напряжённое состояние.
Обратная задача: зная напряжённое состояние, находим на внешней
границе нагрузку.В ТПНС чаще всего решается обратная задача.
Fu – предельная (разрушающая) нагрузка.
Слайд 44
Предпосылки ТПНС:
В каждой точке призмы выпора наступило ПНС (состояние начала
разрушения грунта)
T Слайд 452. Грунт в пределах призмы выпора однороден.
3. Подошва фундаментной конструкции
плоская.
4. ТПНС действует только для малозаглублённых фундаментов, когда поверхность скольжения
выходит на поверхность грунтового массива с образованием призмы выпора.Слайд 48В результате строгого интегрирования системы (*)
мы получаем:
1. Функцию предельной
нагрузки на загруженном участке;
2. Функцию очертаний призмы выпора.
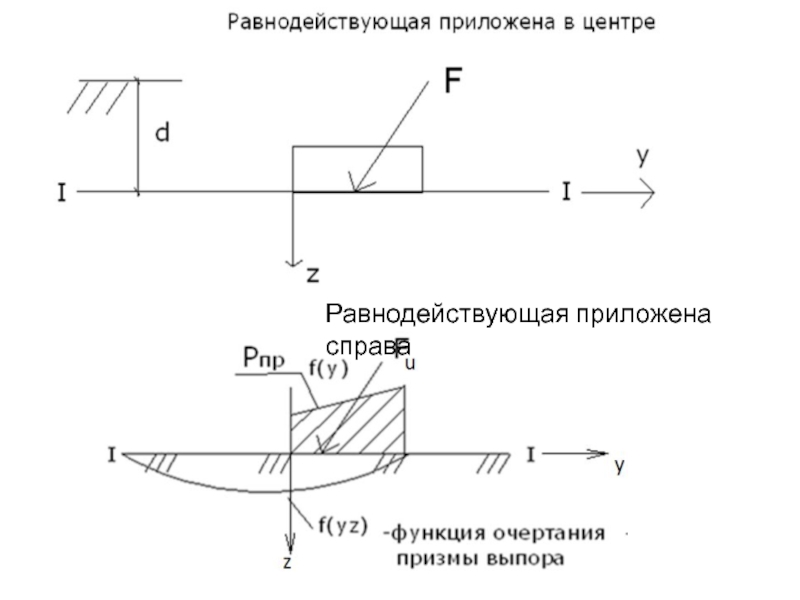
Слайд 50F ≤ Fu - расчет оснований по I п.с.
f(y) –
функции предельных давлений;
f(y z) – функции очертаний призмы выпора;
F –
расчётная нагрузка на основание;Fu – предельная (разрушающая) нагрузка.
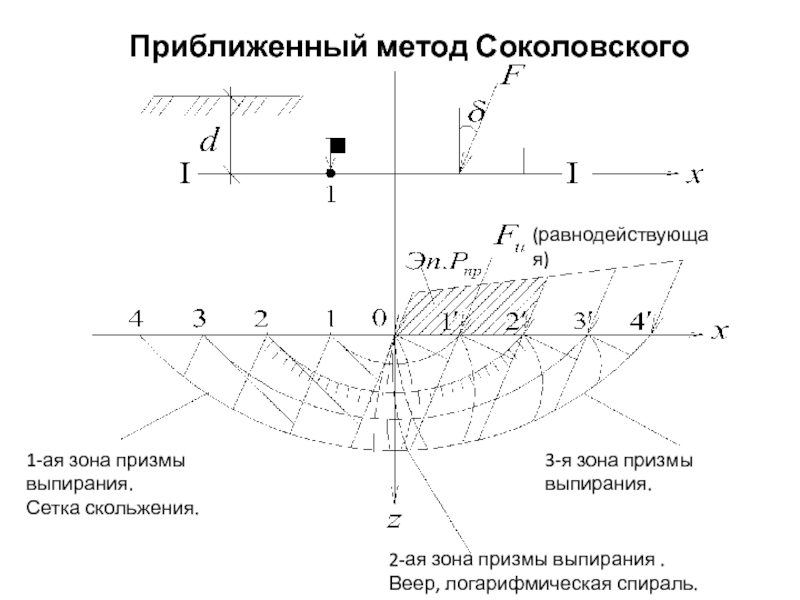
Слайд 51Приближенный метод Соколовского
(равнодействующая)
1-ая зона призмы выпирания.
Сетка скольжения.
2-ая зона призмы выпирания
.
Веер, логарифмическая спираль.
3-я зона призмы выпирания.
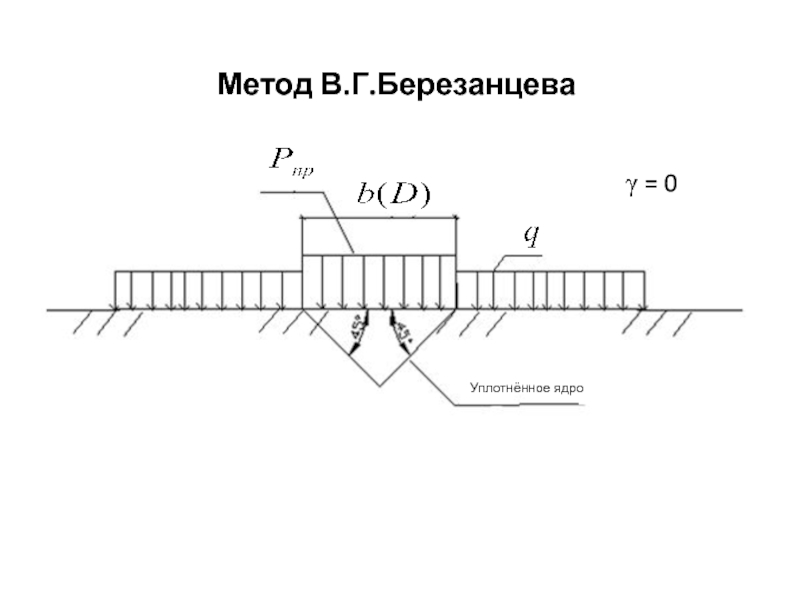
Слайд 53Решение для осесимметричной нагрузки В.Г.Березанцева
При полосовой нагрузке:
,
При круглом
фундаменте:
Слайд 54где N с соответствующими индексами – табличные коэффициенты несущей способности,
принимаемые в зависимости от угла внутреннего трения φ;
γ и γ'
– средний удельный вес грунта соответственно ниже и выше подошвы фундамента;b – ширина ленточного фундамента;
D – диаметр круглого фундамента;
d – глубина заложения подошвы фундамента;
с – удельное сцепление грунта.
Для идеально связных ( φ = 0, с ≠ 0) по Прандтлю:
При круглом фундаменте по А.Ю.Ишлинскому:
Слайд 55Для сыпучих грунтов (В.Г.Березанцев):
Плоская задача -
Пространственная задача -
где
Аn и Ак – обобщенные коэффициенты несущей способности для сыпучих
грунтов, определяемые по номограммам как функции угла и относительной глубины заложения фундамента h/b.
– ширина стороны квадратной или диаметр круглой
площади подошвы фундамента.
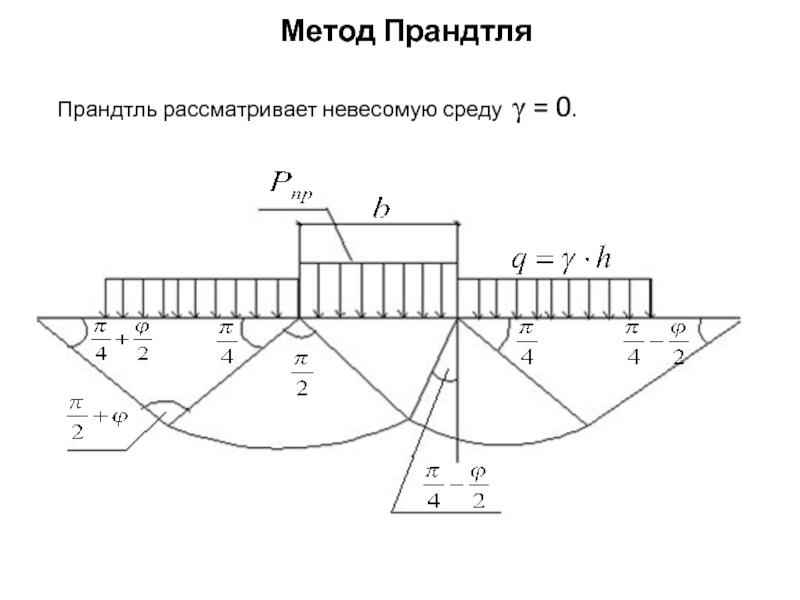
Слайд 57Формула Прандтля:
q – интенсивность нагрузки собственного веса фундамента;
с и ϕ-
прочностные характеристики грунта под подошвой фундамента.
Слайд 58Формула Березанцева:
- табличные коэффициенты, зависящие от угла внутреннего
трения грунта → f (φ);
γ и γ ’ - средний
удельный вес грунта ниже и выше подошвы фундамента соответственно;D – диаметр круглого фундамента.
Метод Голушкевича С.С. (графоаналитический)
γ ≠ 0
Слайд 61Fu - предельное (разрушающее) значение равнодействующей всех сил, приложенных к
основанию;
Nu – её вертикальная составляющая;
Tu – горизонтальная составляющая;
δ - угол
наклона равнодействующей к вертикали;0’ – точка приложения равнодействующей;
– эксцентриситет приложения равнодействующей в направлении размера подошвы l;
– то же, в направлении стороны b.
- приведённые размеры подошвы.
- ядро сечения.
Слайд 62
табличные коэффициенты, зависящие от φ, δ→ f (φ, δ);
табличные
коэффициенты, зависящие от
соотношения размеров → f(b, l) или
(b’, l’);d - глубина заложения подошвы фундамента.