Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Федеральное государственное автономное образовательное учреждение высшего
Содержание
- 1. Федеральное государственное автономное образовательное учреждение высшего
- 2. Готфрид Лейбниц:БиографияЗнакомство с Петром IНаучная деятельностьДвоичная система счисления:ИсторияОперацииПреобразованияПрименениеСодержание
- 3. Готфрид Вильгельм фон ЛейбницДаты жизни: 1646-1716Немецкий философ,
- 4. Вырос в семье профессора философии.К 12-ти годам
- 5. Во время 1670-1672г. Лейбниц работает советником курфюрста
- 6. В 1673г. Лейбниц изобретает собственную конструкцию арифмометра, умеющую выполнять умножение, деление и извлечение корней.
- 7. Первая встреча произошла в 1697г. Встречи с
- 8. В 1684г. Лейбниц публикует первую в мире
- 9. В 1695г. Лейбниц вводит показательную функцию в
- 10. Двоичная система счисления — это позиционная система
- 11. История двоичной системы счисления начинается в Древнем
- 12. Прообразом баз данных, широко использовавшихся в Центральных
- 13. В 1605 году Френсис Бэкон описал систему,
- 14. В 1854 году английский математик Джордж Буль
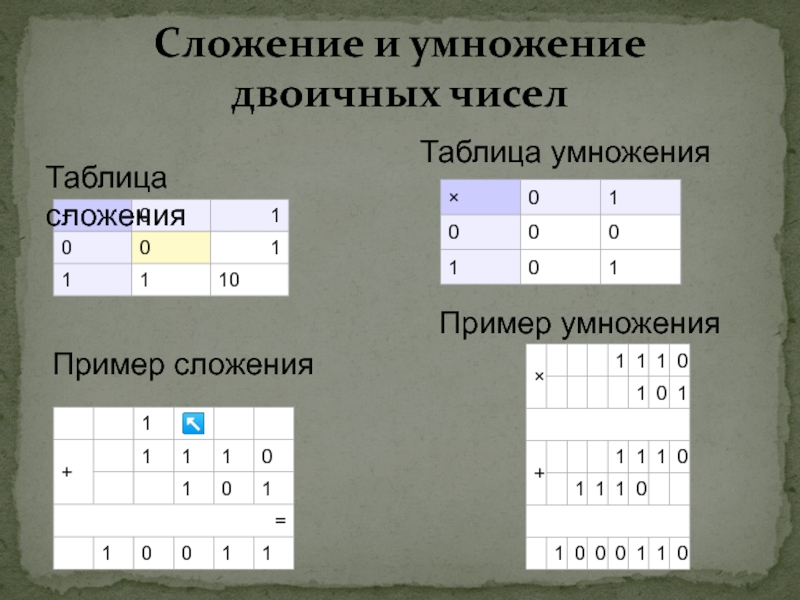
- 15. Сложение и умножение двоичных чисел
- 16. Допустим, вам дано двоичное число 110001. Для
- 17. Допустим, нам нужно перевести число 19 в
- 18. Двоичная система используется в цифровых устройствах, поскольку является
- 19. Сайт http://ru.wikipedia.orgСайт http://www.leibniz-translations.comСписок используемой литературы
- 20. Скачать презентанцию
Слайды и текст этой презентации
Слайд 1Презентация на тему: «Готфрид Лейбниц и двоичная система счисления».
Федеральное государственное
автономное образовательное
учреждение высшего профессионального образования
«ЮЖНЫЙ ФЕДЕРАЛЬНЫЙ УНИВЕРСИТЕТ»
Экономический факультет
Слайд 2Готфрид Лейбниц:
Биография
Знакомство с Петром I
Научная деятельность
Двоичная система счисления:
История
Операции
Преобразования
Применение
Содержание
Слайд 3Готфрид Вильгельм фон Лейбниц
Даты жизни: 1646-1716
Немецкий философ, математик, физик, юрист,
дипломат, изобретатель, языковед.
Наибольшую известность получил благодаря открытию дифференциально-интегрального счисления, а
так же создал комбинаторику как науку.Слайд 4Вырос в семье профессора философии.
К 12-ти годам самостоятельно изучил латынь.
В
15 лет поступил в Лейпцигский университет.
В 1666г, в возрасте 20
лет защитил докторскую диссертацию по праву в Нюрнбергском университете в Альтдорфе.В этом же году он написал первое из своих сочинений «О комбинаторном искусстве», тем самым опередив время на два века, задумав проект математизации логики.
Биография
Слайд 5Во время 1670-1672г. Лейбниц работает советником курфюрста Майнцского по юридическим
и торговым делам. В это же время знакомится с Гюйгенсом
и учится у него математике.В 1675 году Лейбниц завершает свой вариант математического анализа, переписывается с Ньютоном, открывает «Основную теорему анализа».
Слайд 6В 1673г. Лейбниц изобретает собственную конструкцию арифмометра, умеющую выполнять умножение,
деление и извлечение корней.
Слайд 7Первая встреча произошла в 1697г. Встречи с Петром I привели
в дальнейшем к одобрению Петром создания Академии наук в Петербурге,
что послужило началом развития научных исследований в России по западноевропейскому образцу.Лейбниц предложил проект научных исследований в России, связанных с её уникальным географическим положением, таких как изучение магнитного поля Земли, отыскание пути из Арктики в Тихий океан, предложил проект движения за объединение церквей, которое должно было быть создано под эгидой русского императора.
Знакомство с Петром I
Слайд 8В 1684г. Лейбниц публикует первую в мире крупную работу по
дифференциальному исчислению: «Новый метод максимумов и минимумов».
В 1685г. Лейбниц даёт
подразделение вещественных чисел на алгебраические и трансцендентные, в печати появляется понятие интеграла.В 1693г. Лейбниц рассматривает вопрос о разрешимости линейных систем и его результат фактически вводит понятие определителя. Однако линейная алгебра возникла только спустя полвека.
Научная деятельность
Слайд 9В 1695г. Лейбниц вводит показательную функцию в самом общем виде:
uv.
В 1702г. совместно с Иоганном Бернулли открыл приём разложения рациональных
дробей на сумму простейших. В 1703г. Лейбниц написал книгу, английское название которой Explanation Of Binary Arithmetic. В ней была полностью описана современная двоичная система.
Слайд 10Двоичная система счисления — это позиционная система счисления с основанием
2. В этой системе счисления числа записываются с помощью двух
символов (0 и 1).На двоичной системе счисления основана вся современная компьютерная техника.
Двоичная система счисления
Слайд 11История двоичной системы счисления начинается в Древнем Китае. Полный набор
из 8 триграмм и 64 гексаграмм, аналог 3-битных и 6-битных
цифр, был известен в древнем Китае в классических текстах книги Перемен.Индийский математик Пингала (200 год до н. э.) разработал математические основы для описания поэзии с использованием первого известного применения двоичной системы счисления.
История
Слайд 12Прообразом баз данных, широко использовавшихся в Центральных Андах (Перу, Боливия)
в государственных и общественных целях в I—II тысячелетии н. э.,
была узелковая письменность Инков — кипу, состоявшая как из числовых записей десятичной системы, так и не числовых записей в двоичной системе кодирования. Кипу впервые в истории человечества использовалось для применения такого способа ведения бухгалтерского учёта как двойная запись.Слайд 13В 1605 году Френсис Бэкон описал систему, буквы алфавита которой
могут быть сведены к последовательностям двоичных цифр. Важным шагом в
становлении общей теории двоичного кодирования является замечание о том, что указанный метод может быть использован применительно к любым объектам.Современная двоичная система была полностью описана Лейбницем в XVII веке в работе Explanation of Binary Arithmetic. В системе счисления Лейбница были использованы цифры 0 и 1, как и в современной двоичной системе. Лейбниц знал о книге Перемен и заметил, что гексаграммы соответствуют двоичным числам от 0 до 111111.
Слайд 14В 1854 году английский математик Джордж Буль опубликовал работу, описывающую
алгебраические системы применительно к логике, которая в настоящее время известна
как Булева алгебра. Его логическому исчислению было суждено сыграть важную роль в разработке современных цифровых электронных схем.В 1937 году Клод Шеннон представил к защите кандидатскую диссертацию «Символический анализ релейных и переключательных схем в MIT», в которой булева алгебра и двоичная арифметика были использованы применительно к электронным реле и переключателям. На диссертации Шеннона по существу основана вся современная цифровая техника.
Слайд 16Допустим, вам дано двоичное число 110001. Для перевода в десятичное
просто запишите его справа налево как сумму по разрядам следующим
образом:Преобразования двоичных чисел в десятичные
Слайд 17Допустим, нам нужно перевести число 19 в двоичное. Вы можете
воспользоваться следующей процедурой :
19 /2 = 9 с остатком 1
9
/2 = 4 c остатком 1 4 /2 = 2 без остатка 0
2 /2 = 1 без остатка 0
1 /2 = 0 с остатком 1
Итак, мы делим каждое частное на 2 и записываем остаток в конец двоичной записи. Продолжаем деление до тех пор, пока в частном не будет 0. Результат записываем справа налево. Т.е. нижнее число будет самым левым и т.д. В результате получаем число 19 в двоичной записи: 10011.
Преобразования десятичных чисел в двоичные
Слайд 18Двоичная система используется в цифровых устройствах, поскольку является наиболее простой и
соответствует требованиям.
Чем меньше значений существует в системе, тем проще изготовить
отдельные элементы, оперирующие этими значениями. В частности, две цифры двоичной системы счисления могут быть легко представлены многими физическими явлениями: есть ток (ток больше пороговой величины) — нет тока (ток меньше пороговой величины), индукция магнитного поля больше пороговой величины или нет (индукция магнитного поля меньше пороговой величины) и т. д.Применение