Слайд 1ФИЗИКА
1.Савельев И. В. Курс общей физики [Текст]: учеб.пособие для вузов:
в 3 т. Т.1.Механика. Молекулярная физика. / И. В. Савельев.
– Изд. 10-е, стер. – СПб. [и др.] : Лань, 2008 – 432 с.
2. Савельев И. В. Курс общей физики [Текст]: учеб.пособие для вузов: в 3 т. Т.2. Электричество и магнетизм. Волны. Оптика. / И. В. Савельев. – Изд. 10-е, стер. – СПб. [и др.] : Лань, 2008 – 496 с.
3.Трофимова Т.И. Курс физики. [Текст]: учебное пособие для инженерно-технических специальностей высших учебных заведений/ Т. И. Трофимова. – 21-е изд., стер. – Москва: Академия, 2015. – 549 с.
4. Волькенштейн В.С. Сборник задач по общему курсу физики [Текст]: для студентов технических вузов/ В. С. Волькенштейн. Изд. 3-е, испр. и доп. – Санкт-Петербург: Книжный мир, 2013. – 327 с.
5. Дмитриева Е.И. Физика для инженерных специальностей [Электронный ресурс]: учебное пособие/ Дмитриева Е.И.— Электрон. текстовые данные.— Саратов: Ай Пи Эр Медиа, 2012.— 142 c.
Слайд 2ФИЗИКА
1. Механика – кинематика, динамика
2. Электричество – электростатика, магнитостатика, электромагнетизм
3.
Оптика – Волновая ( интерференция, дифракция, поляризация), квантовая
4. Молекулярная
физика и термодинамика, явления переноса
Слайд 3МЕХАНИКА
изучает движение тел , т.е. изменение положения тела или его
частей в пространстве относительно друг друга
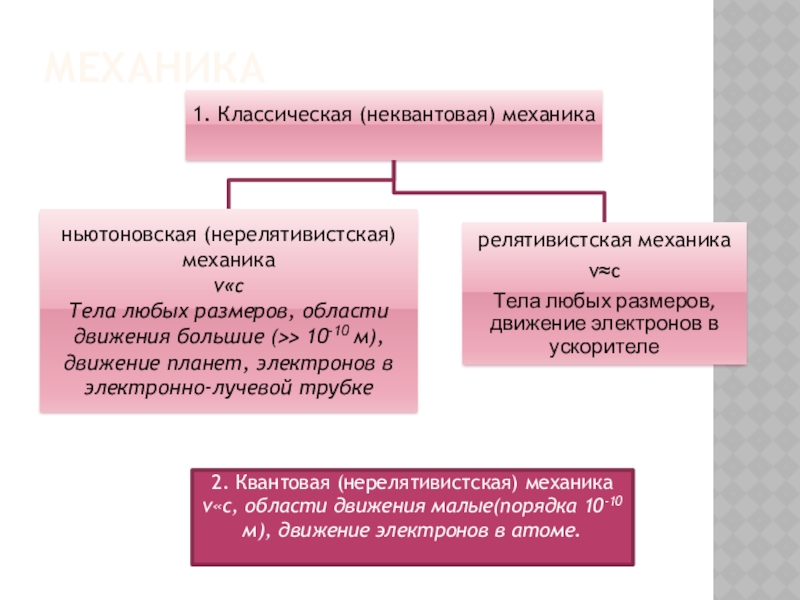
Слайд 4МЕХАНИКА
2. Квантовая (нерелятивистская) механика
v«c, области движения малые(порядка 10-10 м), движение
электронов в атоме.
Слайд 5В механике используют две модели: материальная точка
и абсолютно твердое
тело.
Слайд 6М а т е р и а л ь н
а я т о ч к а
- это
тело , обладающее массой , размерами и формой которого можно пренебречь в условиях данной задачи.
Тело считается материальной точкой, если :
расстояние, которое проходит
тело > > размеров тела;
расстояние от тела до других
тел > > размеров тела.
Слайд 7Например:
движение спутника вокруг Земли;
трансконтинентальный полет самолета.
Слайд 8 Абсолютно твердое тело
- тело деформациями которого можно
в условиях
данной задачи пренебречь.
Слайд 10Кинематика
– раздел механики, в котором
изучается механическое движение материальной точки
(тела)
без рассмотрения причин, по которым это движение происходит.
Слайд 11Основные понятия кинематики
Механическим движением тела называют изменение его положения в
пространстве относительно других тел с течением времени.
Механическое движение относительно. Движение
одного и того же тела относительно разных тел оказывается различным.
Слайд 12М е х а н и ч е с к
о е д в и ж е н и
е т е л а
– процесс, при котором с течением времени изменяется положение тела или частей тела в пространстве относительно других тел.
Слайд 13Для определения положения материальной точки в пространстве
и описания ее
движения необходимо выбрать систему отсчета.
Х
У
Z
Слайд 14Система отсчета
состоит из тела отсчета,
связанной с ней системой
координат
и часов, неподвижных
относительно тела отсчета.
Слайд 15Для того, чтобы выбрать систему отсчета нужно:
Выбрать объект, относительно которого
будет рассматриваться движение, т.е. выбрать
тело отсчета;
2. Выбрать систему координат, начало
которой должно совпадать с одной из точек тела отсчета;
3. Выбрать начало отсчета времени.
Слайд 16Тело отсчета
– произвольно выбранное тело, относительно которого определяется положение
других (движущихся тел).
Положение любого движущегося тела определяется по отношению
к
телу отсчета.
Поэтому механическое движение
всегда относительно.
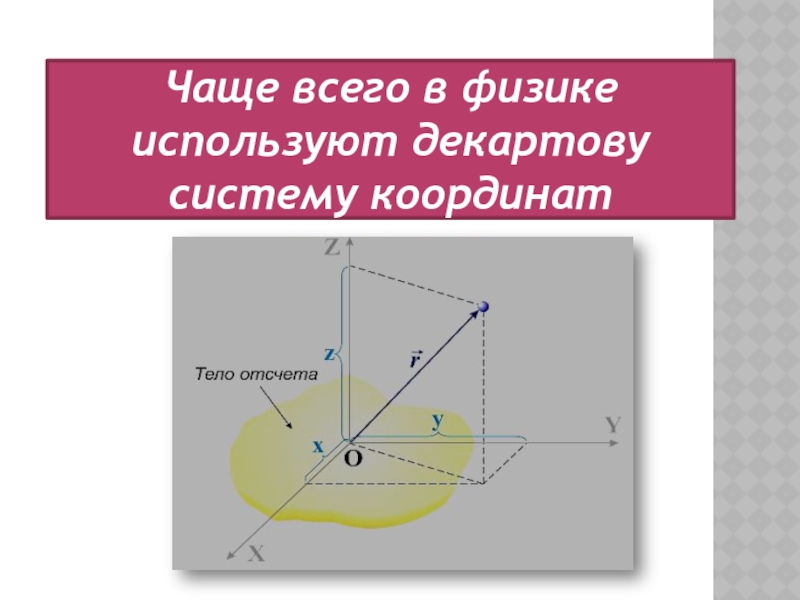
Слайд 17Чаще всего в физике используют декартову систему координат
Слайд 18Определение положения точки в пространстве
Слайд 19Движение одного и того же объекта в разных системах отсчета
выглядит по разному.
ТРАЕКТОРИЯ МАРСА
Слайд 20Положение материальной точки
в данной системе отсчета определяется или ее
координатами
или радиусом – вектором.
Слайд 22При движении материальной точки относительно выбранной системы отсчета она последовательно
занимает различные положения, которые следуют непрерывно
одно за другим,
т.е.
материальная точка описывает воображаемую линию
- траекторию.
Слайд 23Траектория – это линия,
которую описывает материальная точка при движении.
Слайд 24В зависимости от формы траектории различают
прямолинейное и криволинейное
движение
материальной точки (тела).
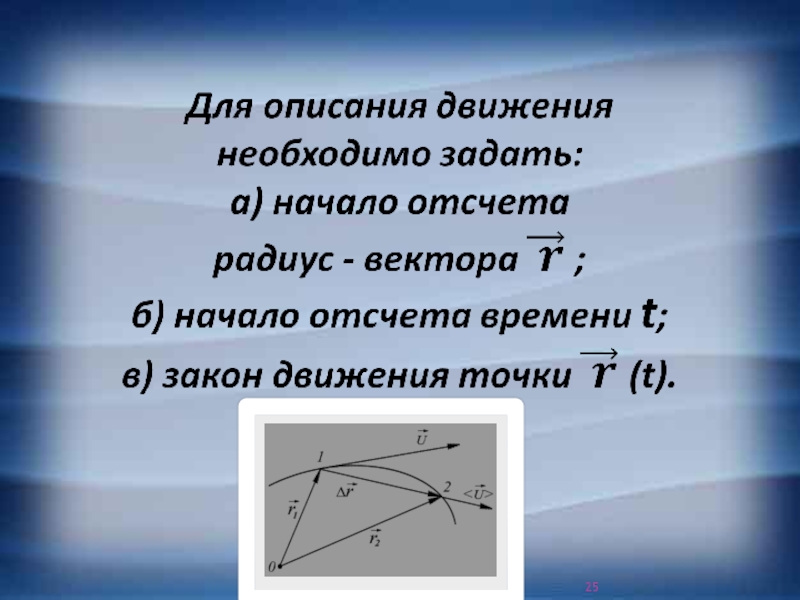
Слайд 26Закон движения
- уравнение в векторной форме, показывающее зависимость
радиус
- вектора от времени.
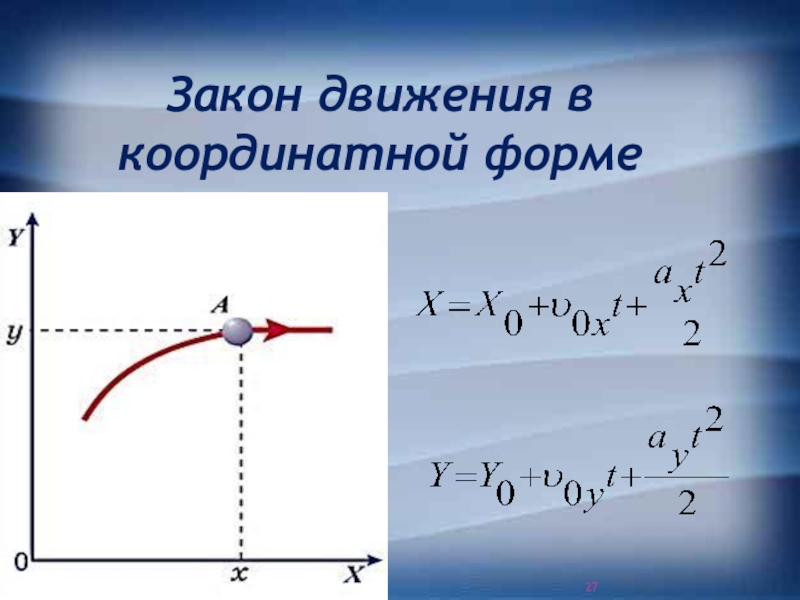
Слайд 27Закон движения в координатной форме
Слайд 28Это наиболее универсальный и часто используемый способ описания движения.
Он
предполагает задание:
а) системы координат ;
б) начала
отсчета времени t;
в) закона движения точки.
Слайд 29Кинематические характеристики движения
Траектория
Путь
Перемещение
Скорость
Ускорение
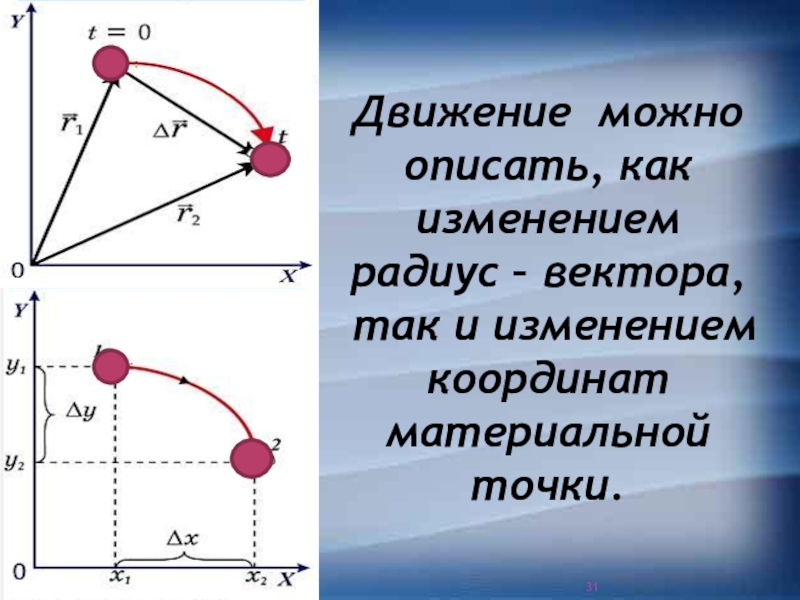
Слайд 31Движение можно описать, как изменением
радиус – вектора,
так и
изменением координат материальной точки.
Слайд 35Быстрота изменения положения материальной точки в пространстве
с течением времени
характеризуется средней и мгновенной скоростью.
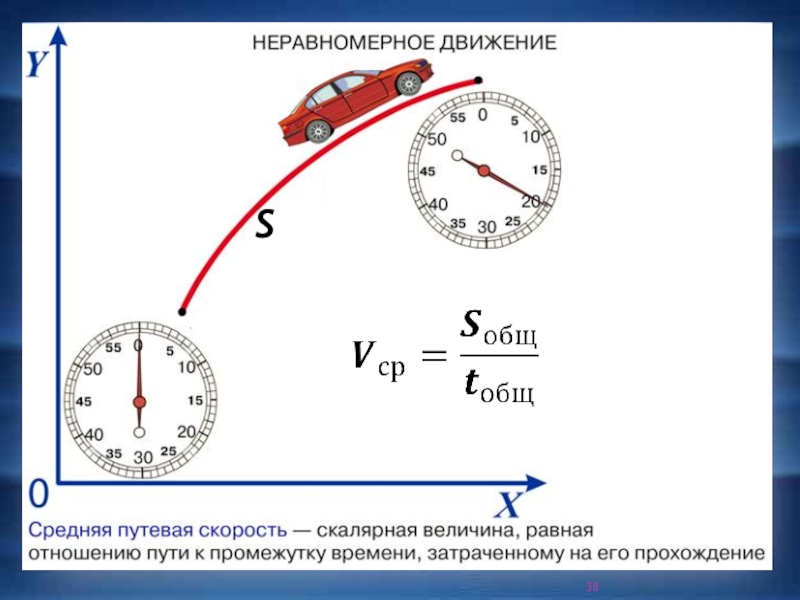
Слайд 36Средняя и мгновенная скорости
Модуль мгновенной скорости материальной точки равен первой
производной ее пути по времени:
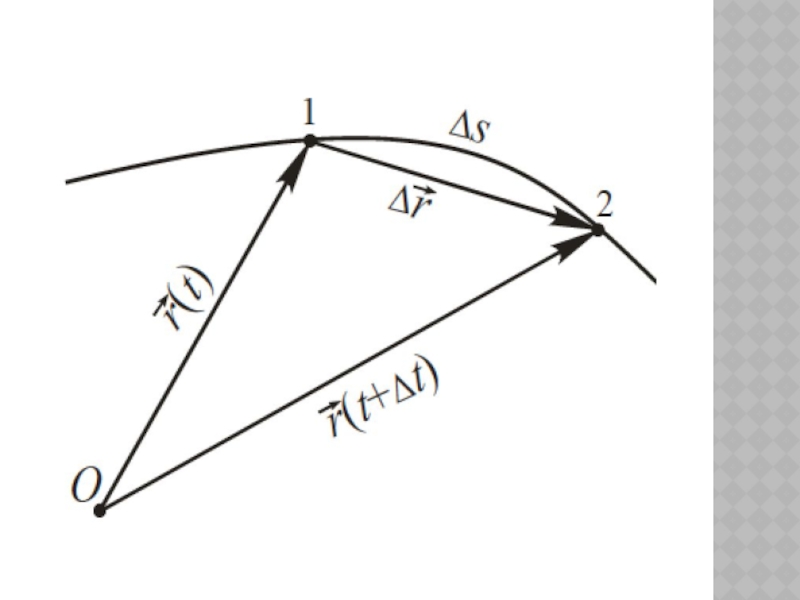
Слайд 37Направление вектора средней скорости совпадает с направлением вектора перемещения.
Слайд 39Изменение вектора скорости по величине и направлению
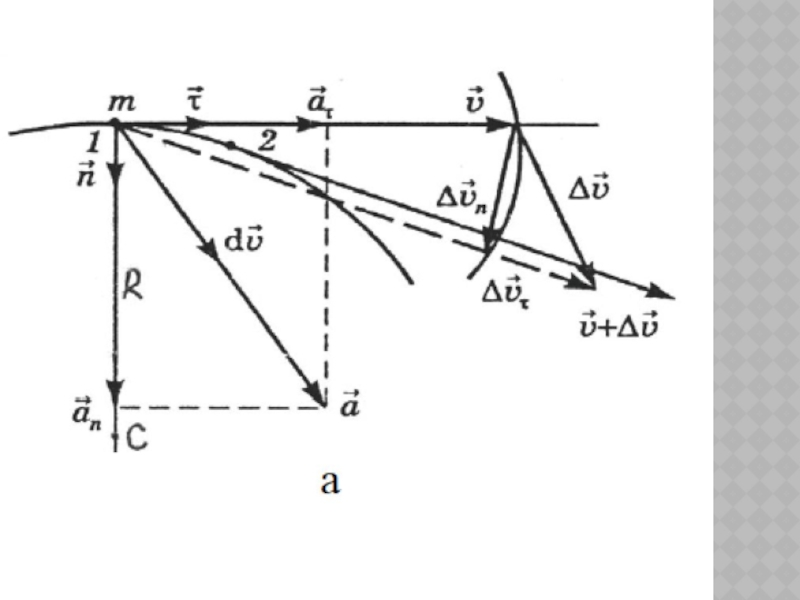
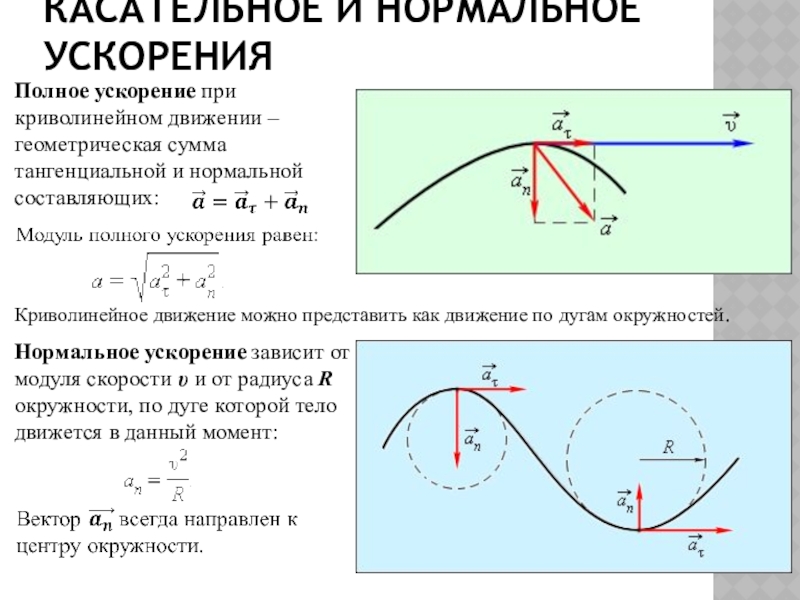
Слайд 46Касательное и нормальное ускорения
Криволинейное движение можно представить как движение по
дугам окружностей.
Нормальное ускорение зависит от модуля скорости υ и от
радиуса R окружности, по дуге которой тело движется в данный момент:
Полное ускорение при криволинейном движении – геометрическая сумма тангенциальной и нормальной составляющих:
Слайд 47В случае движения по окружности нормальное ускорение называется центростремительным.
При
движении по окружности с постоянной скоростью нормальное ускорение постоянно по
модулю и направлено к центру окружности.
Слайд 48Направление вектора тангенциального ускорения совпадает с направлением линейной скорости или
противоположно ему.
Слайд 50КИНЕМАТИКА ВРАЩАТЕЛЬНОГО ДВИЖЕНИЯ
ТВЕРДОГО ТЕЛА
Слайд 51Движение твердого тела отличается от движения материальной точки. Обычно выделяют
два простых вида движения тела:
Поступательное - это движение, при котором
любая прямая, проведенная в теле, перемещается параллельно самой себе так, что все точки тела описывают одинаковые траектории.
Вращательное - это движение, при котором все точки тела двигаются по окружностям разных радиусов, центры которых лежат на одной прямой, называемой осью вращения.
Сложное движение твердого тела – это совокупность поступательного и вращательного движений.
Абсолютно твердым называется тело, конфигурация которого не меняется при любых воздействиях на него.
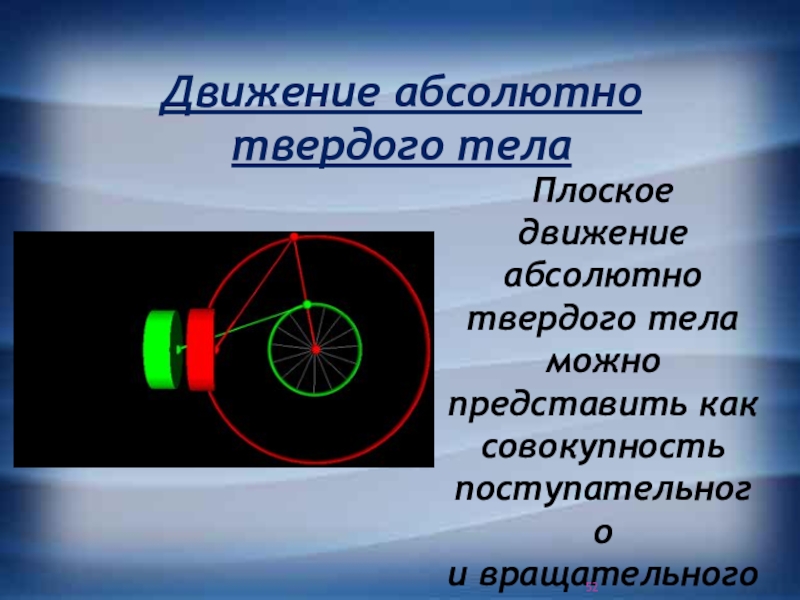
Слайд 52Плоское движение абсолютно твердого тела можно представить как совокупность поступательного
и вращательного движений.
Движение абсолютно твердого тела
Слайд 53Поступательным движением называется такое движение,
при котором траектории всех точек тела
одинаковы, или при котором любой отрезок, проведенный в теле перемещается
параллельно самому себе.
Слайд 54Вращательным движением называется такое движение,
при котором траектории всех точек
тела – это окружности, а центры этих окружностей лежат на
одной прямой называемой осью вращения.
Слайд 55При вращательном движении,
в отличие от поступательного,
скорости разных точек
тела неодинаковы.
Поэтому скорость какой-либо точки вращающегося тела не может служить
характеристикой движения всего тела.
Слайд 56Кинематические характеристики вращательного движения
1. Угол поворота
2. Угловая скорость
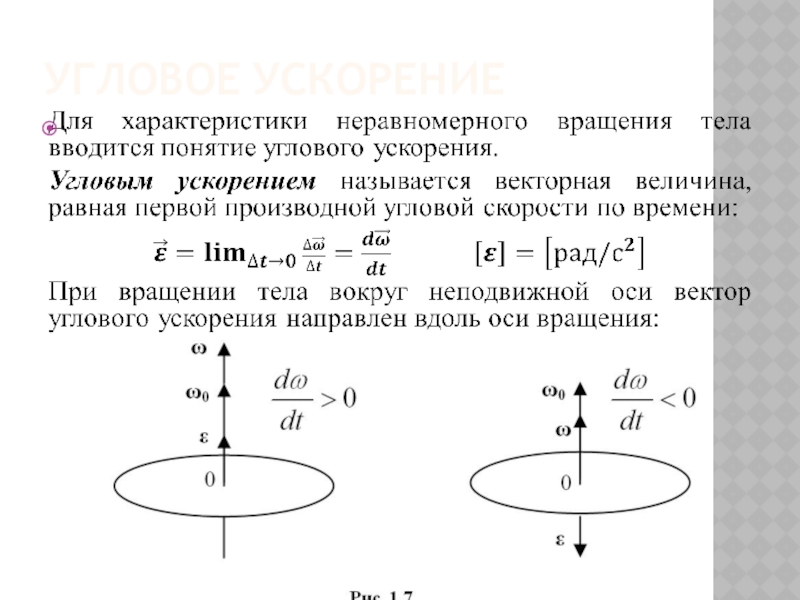
3. Угловое ускорение
Слайд 58Угловая скорость
Угловая скорость может быть связана с линейной скоростью υ произвольной точки А.
Пусть за время Δt точка проходит по дуге окружности длину пути Δs. Тогда
линейная скорость точки будет равна:
Слайд 59Угловая скоpость показывает, на какой угол повоpачивается тело за 1
секунду.
Слайд 63Характеристики равномерного вращения
Если ω = const, то вращение называется равномерным.
Равномерное вращение
можно характеризовать периодом вращения Т – временем, за которое точка тела совершает один
полный оборот, т.е. поворачивается на угол 2π:
Число полных оборотов, совершаемых телом при равномерном движении по окружности, в единицу времени называется частотой вращения:
Слайд 66Связь между линейными и угловыми характеристиками
Выразим тангенциальную и нормальную составляющие
ускорения точки A вращающегося тела через угловую скорость и угловое ускорение:
Связь между
линейными (длина пути s, пройденного точкой по окружности радиуса R, линейная скорость v, тангенциальное ускорение aτ, нормальное ускорение an) и угловыми характеристиками (угол поворота φ, угловая скорость ω, угловое ускорение ε) выражается следующими формулами:
Слайд 67По аналогии с уравнениями поступательного движения можно записать уравнения для
вращательного движения
Слайд 69По аналогии с уравнениями поступательного движения можно записать уравнения для
вращательного движения
r
dt
Слайд 74Кинематические уравнения поступательного и вращательного движений
![Презентация на тему ФИЗИКА1.Савельев И. В. Курс общей физики [Текст]: учеб.пособие ФИЗИКА1.Савельев И. В. Курс общей физики [Текст]: учеб.пособие для вузов: в 3 т. Т.1.Механика. Молекулярная физика. /](/img/tmb/7/609354/e99023ff060f61317e47b67e6d32be3e-800x.jpg)