Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Физика реального кристалла
Содержание
- 1. Физика реального кристалла
- 2. Дислокационные стенки
- 3. Стабильные конфигурации краевых дислокацийСтабильные дипольные конфигурации для дислокаций противо- положного знакаСтабильнаяконфигурациядля дислокаций одного знака
- 4. Слайд 4
- 5. b/h
- 6. Малоугловая граница блоков
- 7. Слайд 7
- 8. Мозаичность кристалловRocking curve – кривая качания
- 9. Дислокационная стенка - двумерный дефект решеткиБлочные кристаллы - малоугловые границы блоков
- 10. Слайд 10
- 11. Задача о дислокационной стенкеM = G/2(1-)
- 12. Поле напряжений прямой краевой дислокации(сплошная изотропная среда)Плоское
- 13. Слайд 13
- 14. Основная формула, используемая для нахожденияэтой суммыпереход накомплекснуюплоскость
- 15. D h; X ; Y
- 16. Для x >> h/2 соотношение (19.75) аппроксимируется выражением
- 17. Распределение напряжений в окрестности дислокационной стенки
- 18. Скольжение +переползание!Процесс полигонизации,приводящий к образованиюмалоугловых границ зерен
- 19. Сравнение законов спадания напряжений с расстоянием r, для точечных дефектов, дислокаций и дислокационных стенок
- 20. Кривизна решетки
- 21. Слайд 21
- 22. 1/R = b
- 23. Подобная ситуация возникает, например,когда кристалл изгибается пластически
- 24. Поле напряжений, порождаемое ансамблем дислокаций
- 25. Линейное натяжение дислокаций
- 26. Линейное натяжение дислокаций (1)/L = /L = Линейное натяжениестремится уменьшитьдлину дислокационнойлинииСила, действующаяна концы линии
- 27. Линейное натяжение дислокаций (2)Сила Пича-Келлера:f/L =
- 28. = Gb/RСила Пича-Келлера:f/L = b = 0 =
- 29. Изгиб линии дислокацииТаким образом, для того, чтобы
- 30. Дислокационные реакции
- 31. Слайд 31
- 32. Дислокационные узлы
- 33. Правило Франкаb32 = b12 + b22 + 2b1b2cos Надо сравнить b32 и b12 + b22 ?
- 34. Слайд 34
- 35. Слайд 35
- 36. Дислокации в гранецентрированной кубической решеткеДислокационные сеткис тройными узлами
- 37. Сетка Франка
- 38. Винтовые или 60 градусныедислокацииПлоскость скольжения (111)
- 39. Слайд 39
- 40. Слайд 40
- 41. Движение дислокаций
- 42. Движение дислокаций является основным механизмом пластической деформации кристаллов исключения: нитевидные кристаллы, углеродные нанотрубки
- 43. Образование ступенек скольженияСдвиговоенапряжение
- 44. Движение дислокаций как механизм пластической деформации
- 45. Дислокационный механизм пластической деформации !!
- 46. Геометрия скольжения
- 47. Наблюдениеполос скольжения
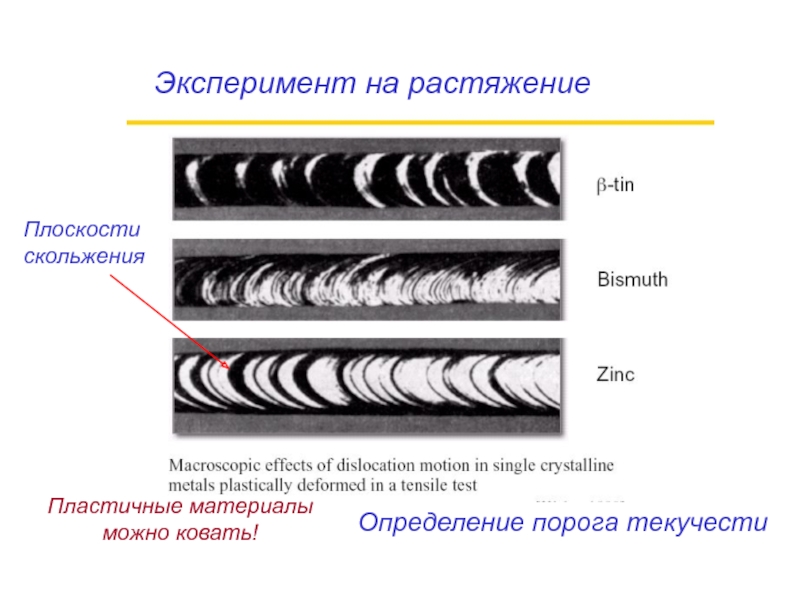
- 48. Эксперимент на растяжениеПлоскости скольженияОпределение порога текучестиПластичные материалыможно ковать!
- 49. Динамический деформационный эксперимент - растяжение образца с постоянной скоростью
- 50. Диаграмма напряжение - деформацияОпределение порогатекучести
- 51. Слайд 51
- 52. Слайд 52
- 53. Измерение скорости движения дислокаций
- 54. Слайд 54
- 55. Экспериментальныеданные
- 56. Скорость движениядислокацийСтепенная зависимость
- 57. ТемпературнаязависимостьСтепенная зависимостьЭкспоненциальная зависимость
- 58. Слайд 58
- 59. V = 0
- 60. ПереползаниеV ≠ 0
- 61. -переползаниеV ≠ 0Перенос вещества посредством диффузии
- 62. Слайд 62
- 63. Слайд 63
- 64. 1 эВЕc 1 эвна связь
- 65. Слайд 65
- 66. Пересечение двух дислокаций
- 67. kinksКонсервативноедвижениеНеконсервативное движениеЕ 1 эвна связь Е 10 -3 эв на связь
- 68. Термическое образование джогов
- 69. Геликоидальные дислокации
- 70. Скачать презентанцию
Дислокационные стенки
Слайды и текст этой презентации
Слайд 1Профессор Б.И.Островский
Физика реального кристалла
ostr@cea.ru
9. Дислокационные стенки. Кривизна
решетки. Линейное
натяжение
Слайд 3Стабильные конфигурации краевых дислокаций
Стабильные дипольные
конфигурации для
дислокаций противо-
положного
знака
Стабильная
конфигурация
для дислокаций
одного знака
Слайд 9Дислокационная стенка - двумерный
дефект решетки
Блочные кристаллы -
малоугловые границы
блоков
Слайд 12Поле напряжений прямой краевой дислокации
(сплошная изотропная среда)
Плоское деформированное
состояние: ux;
uy; uz = 0
ux = ux(x,y)
uy = uy(x,y)
-1 <
< 1/2E =2G (1+ )
Слайд 18Скольжение +
переползание!
Процесс полигонизации,
приводящий к образованию
малоугловых границ зерен
Слайд 19Сравнение законов спадания напряжений с расстоянием r,
для точечных дефектов,
дислокаций и
дислокационных стенок
Слайд 23Подобная ситуация возникает, например,
когда кристалл изгибается пластически
(не упруго!) до
радиуса изгиба R
= 1/bR
ds = Nb
= N/A
lattice spacing
a = b
Слайд 26Линейное натяжение дислокаций (1)
/L =
/L =
Линейное натяжение
стремится уменьшить
длину
дислокационной
линии
Сила, действующая
на концы линии
Слайд 27
Линейное натяжение дислокаций (2)
Сила Пича-Келлера:
f/L = b
=
- напряжение от внешнего источника
bdl = 2Tsin(d/2) Td
Gb2ddl = Rd
= Gb/R
Слайд 29Изгиб линии дислокации
Таким образом, для того, чтобы изогнуть дислокацию
в
кривую с эффективным радиусом R, необходимо
приложить к образцу напряжение:
= Gb/R
R
F2
F1
F2/l– F1 /l = T/l = Gb2/l = Gb2/R =
= b
l
F1 = F2
Слайд 42Движение дислокаций является основным механизмом пластической деформации кристаллов исключения: нитевидные кристаллы,
углеродные нанотрубки
Слайд 48Эксперимент на растяжение
Плоскости
скольжения
Определение порога текучести
Пластичные материалы
можно ковать!
