Физика твердого тела Курс лекций (9) 1. Теплоемкость газа свободных

Электропроводность и закон Ома в квантовом представлении
3. Теплопроводность металлов

и закон Видемана-Франца в квантовомеханическом представлении.
4. Взаимодействие электромагнитных волн с металлами

теплоемкости металла, тогда как эксперимент показывает, что электронный вклад в

теплоемкость при комнатной температуре составляет не более 1% от предсказанной классической теорией величины.

Причина этого противоречия связана с тем, что не каждый электрон, как это следовало бы из классической модели, при нагревании кристалла получает энергию (3/2)kТ . На самом деле такую энергию получают только электроны, имеющие энергию Е вблизи Ef.

Выполним расчет электронного вклада в теплоемкость металла при низких температурах. Полная энергия и полное число электронов в газе свободных электронов может быть рассчитано как:

если учесть, что величина kБТ мала по сравнению с энергией

Ферми.

Рассмотрим интеграл общего вида:

Интегрируя I по частям, имеем:

Первый член в обращается в нуль, так как

Чтобы вычислить второй член

разложим функцию G(e) в окрестности

виде могут быть записаны так:
Такой интеграл имеет табличное значение:

получаем:
Итак, уровень Ферми всегда меньше энергии Ферми, но при низких

температурах второй член имеет значение ~10-4 и менее.

Вычислим энергию газа свободных электронов при низких температурах:

выражение:
Подставляя получаем соотношение для электронной теплоемкости
Вклад в теплоемкость, связанный с

электронами, при низких температурах пропорционален абсолютной температуре.

При низких температурах теплоемкость металлов при постоянном объеме может быть записана в виде суммы двух членов, первый из которых описывает вклад свободных электронов, а второй – колебаний решетки:

различимой лишь при очень низких температурах.
Действительно, для отношения решеточной и

электронной теплоемкостей при низких температурах имеем:

Следовательно, вклад электронной теплоемкости может превышать решеточный лишь при температурах T ниже 1 K. При более высоких температурах главным
становится «решеточный» вклад, на фоне которого малое значение электронной теплоемкости становится неразличимым. Тем самым преодолевается противоречие, присущее классической теории электронных свойств металлов.

Температура Дебая приближённо указывает температурную границу, ниже которой
начинают сказываться квантовые эффекты при колебаниях решетки.

с волновым вектором соотношением:
На отрицательно заряженную частицу со стороны электрического

поля действует сила:

Тогда второй закон Ньютона для электронов может быть записан в виде:

После интегрирования имеем

Если включить электрическое поле в момент времени t = 0, то электроны, запол-
нявшие сферу Ферми в момент включения поля так, что ее центр находился в начале координат k - пространства, спустя время dt приобретут некоторое приращение импульса.
То есть под действием электрического поля каждый электрон, находившийся
в исходном состоянии с волновым вектором k , изменит свое состояние так, что его волновой вектор изменится на величину:

электрическом поле
Электроны будут по-прежнему заполнять сферу энергетического пространства, однако положение

ее центра оказывается смещенным на величину

Полный импульс системы из N электронов будет равен:

теории при действии электрического поля в течение неограниченно
большого промежутка времени

положение сферы Ферми должно постоянно изменяться пропорционально времени. Однако этого не происходит.

Сфера Ферми стационарно сохраняет свое смещенное положение вследствие столкновения электронов с примесями, дефектами решетки или фононами.

Если бы центров рассеяния электронов не существовало, то под действием постоянной силы электроны должны двигаться равноускоренно.

Однако дефекты строения и колебания решетки оказывают тормозящее действие на электроны, благодаря чему электроны движутся с некоторой постоянной средней (дрейфовой) скоростью, обусловленной наличием постоянного электрического поля.

стационарное смещение сферы Ферми в данном поле определяется соотношением:
откуда для

приращения скорости получим:

В соответствие со сферой Ферми, новое положение занимают электроны, находящиеся вблизи поверхности Ферми, и, обладающие наибольшей энергией Ферми. Именно эти электроны участвуют в создании тока.

То есть в переносе тока участвует только небольшая часть свободных электронов, близкая к поверхности Ферми.

выражение - закона Ома. Коэффициент пропорциональности между током и напряжением

является удельная электропроводность:

Удельное электрическое сопротивление есть величина, обратная электропроводности:

Известно, что скорость Ферми-электронов не зависит от температуры:

-длина свободного
пробега

Ферми-электронов.

Из эксперимента:  для проводников при T = 20оС

равна ~ n*100 A
и увеличивается при понижении температуры.
 - гораздо больше межатомных расстояний.

Отсюда возникают два вопроса:
Почему не происходят ожидаемые упругие соударения электронов с атомами, расстояние между которыми 1-3 ангстрема ?
2. Какие процессы рассеяния на самом деле определяют среднюю длину свободного пробега электронов проводимости в металлах?

Определение:
Фонон - процесс волнового колебания атомов в решетке, с частотой, кратной некоторому определенному малому значению (квантуется).

В соотношении :

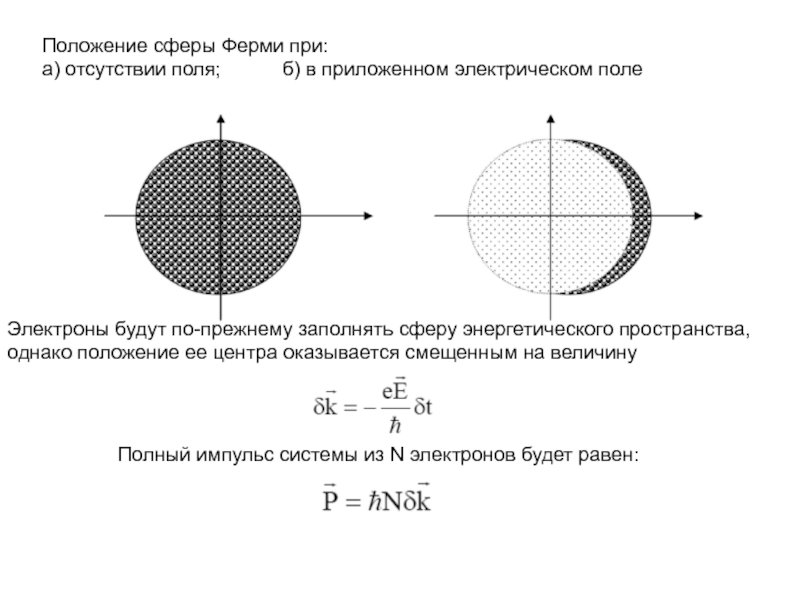
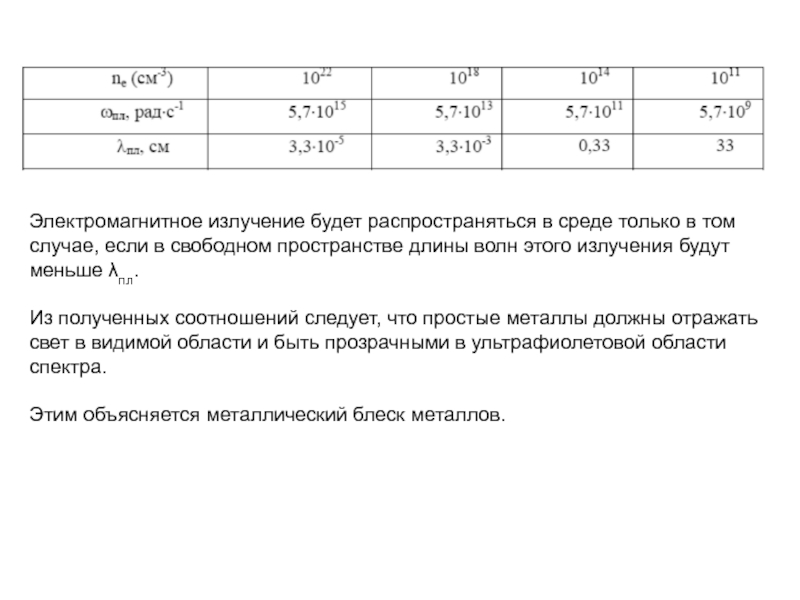
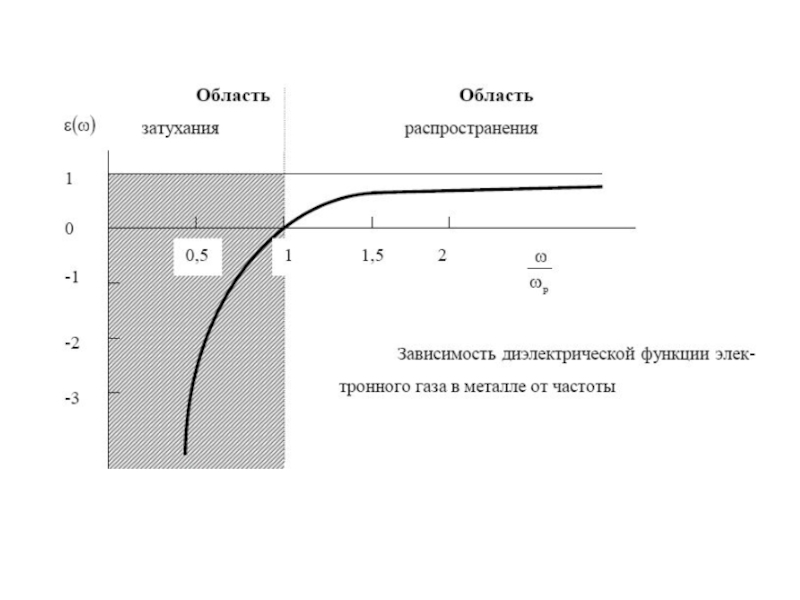
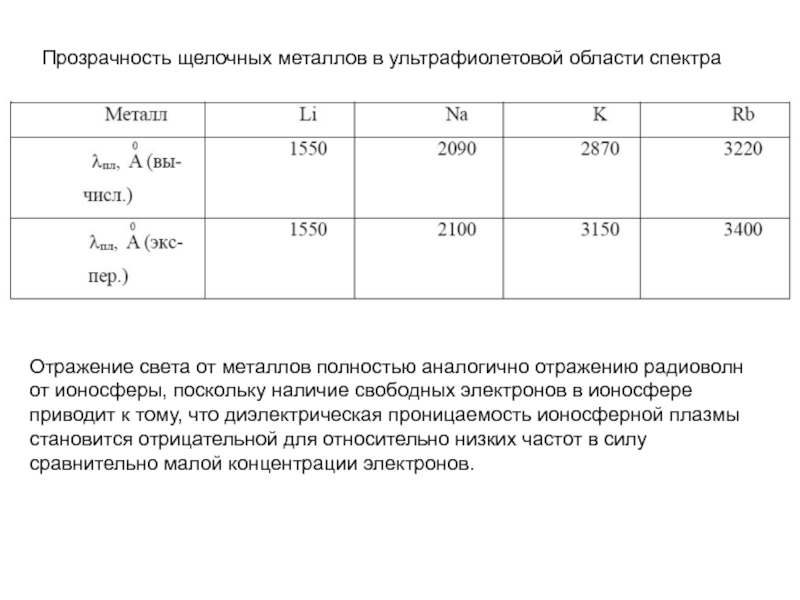
кристалле как волны, которая в периодической среде распространяется беспрепятственно.

Рассеяние электронной

волны может происходить при нарушении регулярности расположения атомов в кристалле – на фононах и дефектах структуры.

Дефекты - посторонние атомы в решетке, вакансии, междоузельные атомы, дислокации, границы зерен и внешние поверхности кристалла.

Средняя длина свободного пробега , обусловленная только рассеянием
на дефектах, не зависит от температуры, в то время как для фононного рассеяния средняя длина свободного пробега будет уменьшаться с увеличением температуры.

При одновременном действии этих двух механизмов средняя длина свободного пробега должна иметь вид:

Матиссена):
Средняя длина свободного пробега, определяемая рассеянием на фононах, для температур,

превышающих температуру Дебая, должна изменяться обратно пропорционально температуре, поскольку при высоких температурах число фононов пропорционально температуре:

Учитывая это, можно объяснить наблюдаемую на опыте линейную зависимость электрического сопротивления металлов от температуры при высоких температурах.

классического представления о теплопроводности с представлением основанным на квантовых свойствах

электронах в металле как Ферми-газе.

Для этого воспользуемся выражением для коэффициента электронной теплопроводности, где вместо средней тепловой скорости подставим скорость Ферми-электронов:

Подставляя величины в квантово-механическом представлении, получим:

– закон Видемана-Франца, который хорошо выполняется для многих чистых металлов.

с частотой  с газом свободных электронов металла.

В отсутствие

столкновений уравнение движения свободного электрона в электрическом поле имеет вид:

то подстановка дает:

Индуцированный полем дипольный момент, связанный с электроном, может быть вычислен так:

а вектор поляризации будет иметь значение:

электронов.
Тогда соотношение примет окончательный вид:
При всех частотах, меньших пл, величина

( ) становится отрицательной.

Для электромагнитных волн справедлив закон дисперсии:

D() –электрическая индукция

Из него следует: ()>0

значениях ( )
Электромагнитная волна при значениях частот 0

 < пл не может распространяться. Из закона дисперсии можно записать:

концентрации электронов

если в свободном пространстве длины волн этого излучения будут меньше

пл.

Из полученных соотношений следует, что простые металлы должны отражать свет в видимой области и быть прозрачными в ультрафиолетовой области спектра.

Этим объясняется металлический блеск металлов.

полностью аналогично отражению радиоволн от ионосферы, поскольку наличие свободных электронов

в ионосфере приводит к тому, что диэлектрическая проницаемость ионосферной плазмы становится отрицательной для относительно низких частот в силу сравнительно малой концентрации электронов.

конструктивной прочности и коррозионной стойкости.

Серебро – один из лучших

проводниковых материалов и применяется в производстве измерительных приборов, для металлизации трактов сверхвысокочастотных устройств, в качестве электродов, вжигаемых в стекло, керамику, кварц. По сравнению с медью более устойчиво к окислению, однако вследствие высокой стоимости применяется в наиболее ответственных узлах и устройствах.

Медь обладает несколько лучшими проводящими свойствами в сравнении с серебром, пластична, имеет удовлетворительную прочность. Широко применяется в качестве проводникового материала в потребительских электрических сетях, в обмотках трансформаторов, дросселей, генераторов, электродвигателей и др. Вследствие недостаточной коррозионной стойкости для проводниковых изделий из меди требуется дополнительная защита. В контактных группах выключателей, расцепителей, автоматов защиты сетей, также применяют более прочные сплавы на основе меди - проводниковые бронзы.

прочности, но вследствие меньшей плотности провод из него при равной

с медным проводимости оказывается легче. Широко применяется в качестве основного материала токонесущих элементов линий передач электрической энергии.
Кроме того, электротехнические изделия из алюминия значительно дешевле медных. Достаточно широко распространено применение алюминия в качестве материала напыляемых в вакууме на различные электронные компоненты (пьезоэлектрические резонаторы и фильтры, ультразвуковые линии задержки на поверхностных акустических волнах и т. п.)
электродов.

Золото - уступает меди и серебру по удельной электропроводности и прочности, практически не окисляется, благодаря чему его используют в самых ответственных соединениях, контактах и токоведущих дорожках при производстве диодов, транзисторов, микросхем и других микроэлектронных компонентов.