Формальна логіка у вирішенні задач діагностики та лікування

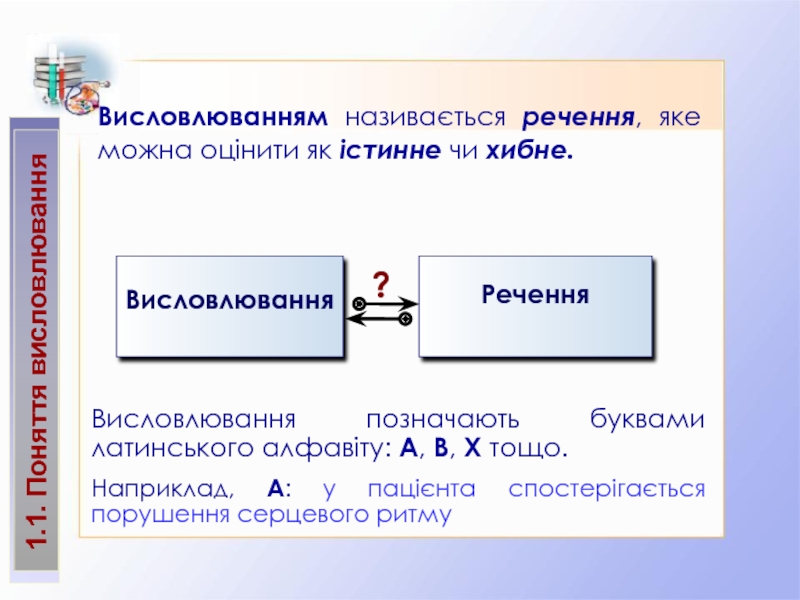
висловлювання
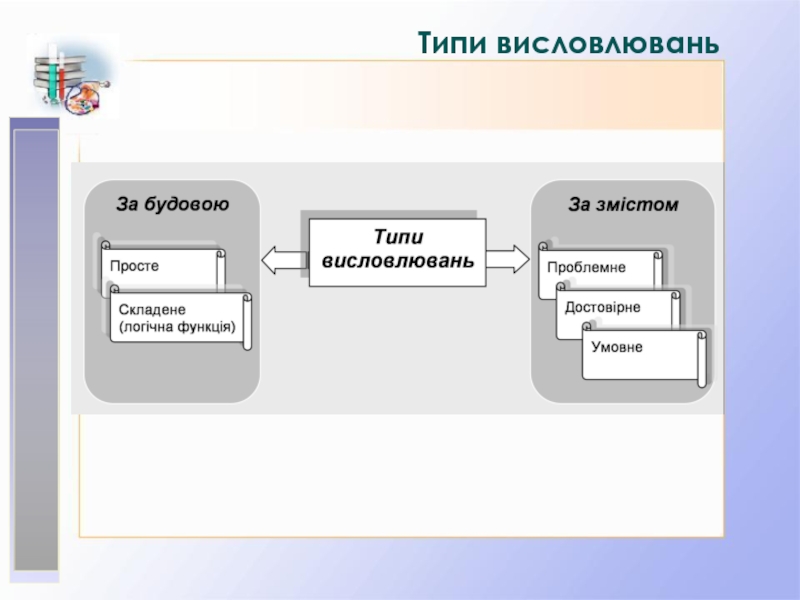
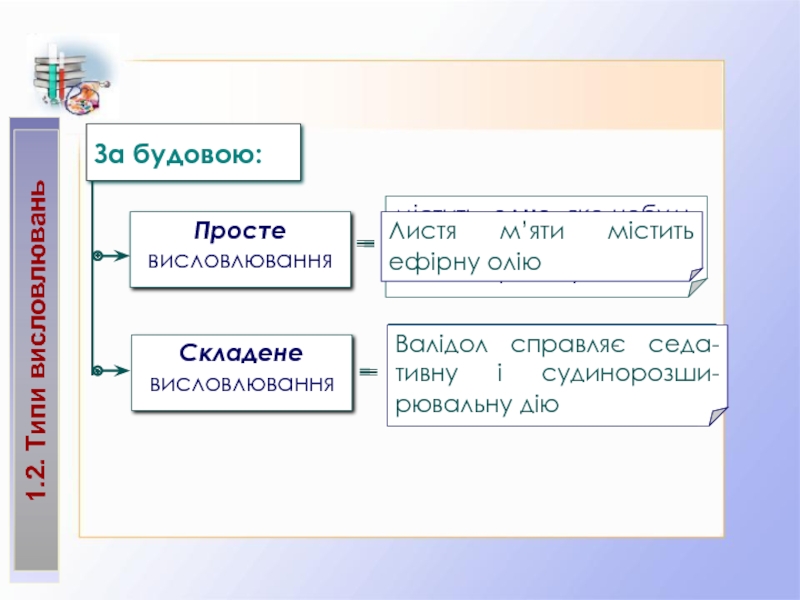
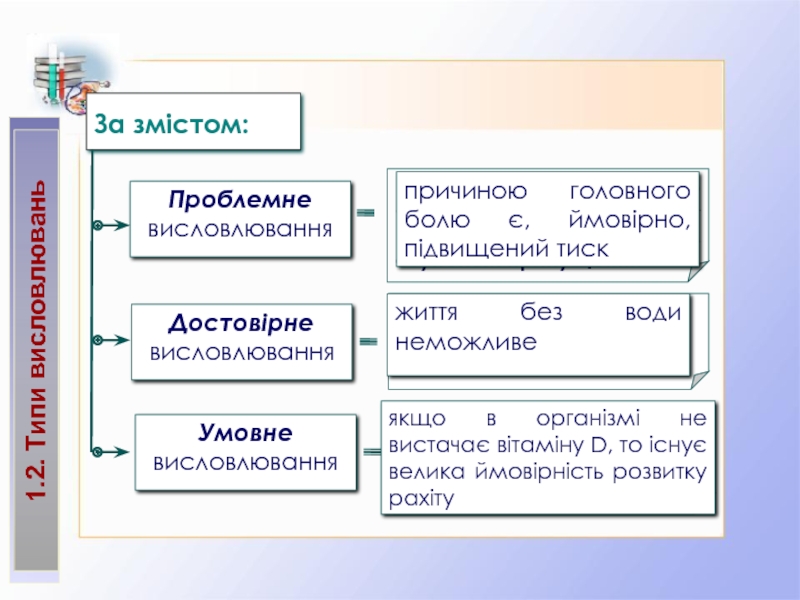
1.2. Типи висловлювань

1.3. Множина значень та алфавіт висловлювання.
Логічні операції та таблиці істинності
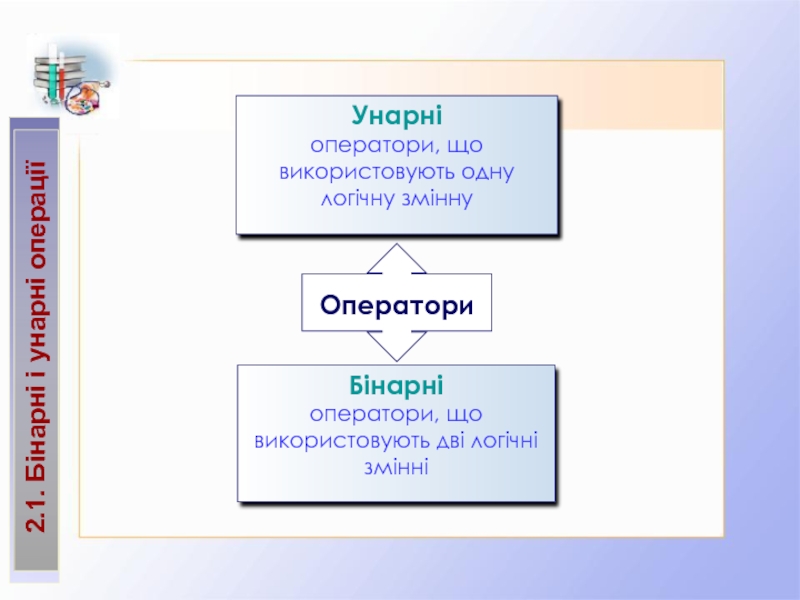
2.1. Бінарні і унарні операції
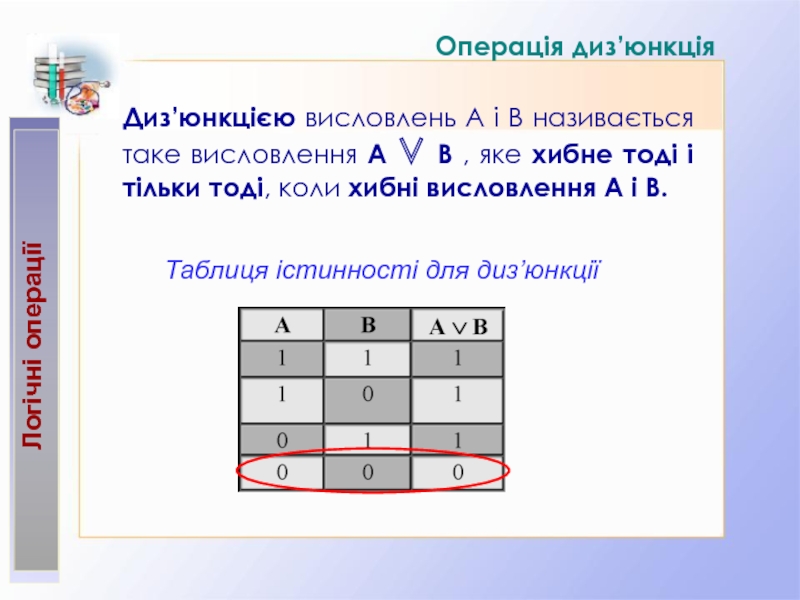
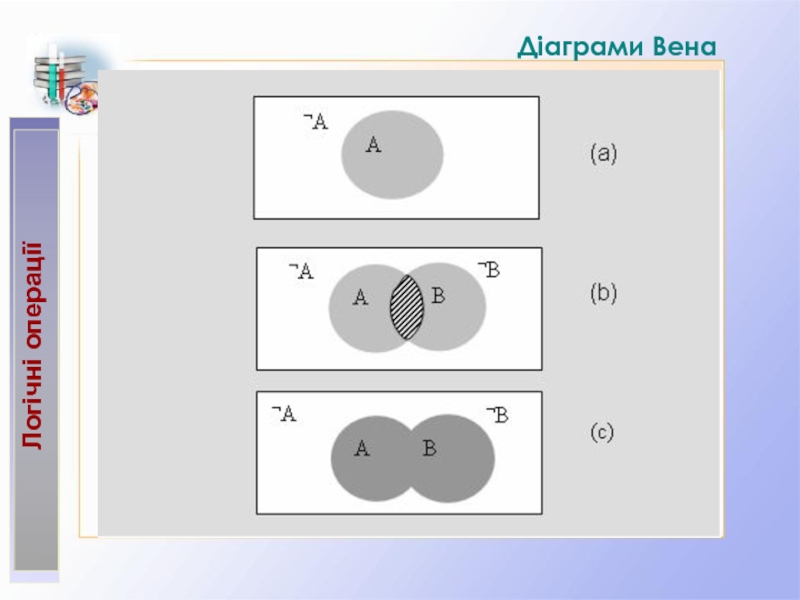
2.2. Основні логічні операції: заперечення, кон’юнкція, диз’юнкція, імплікація, еквіваленція
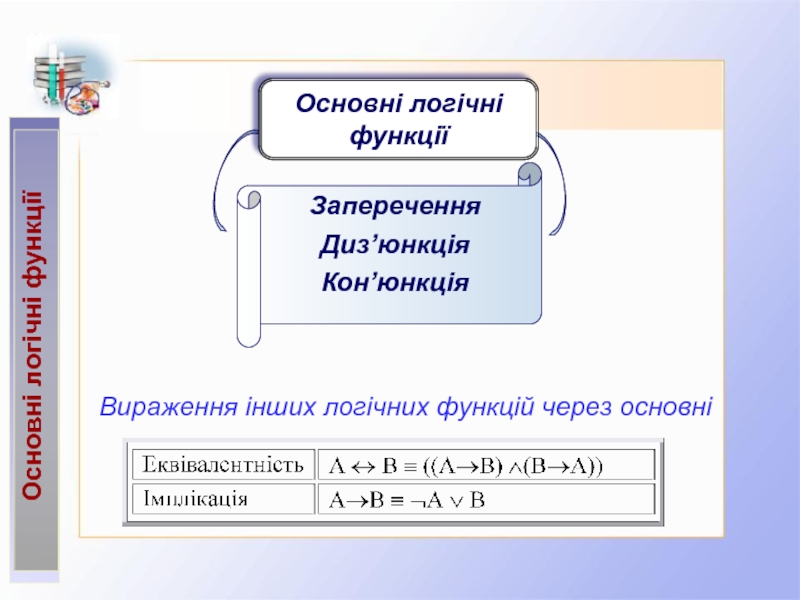
2.3. Основні логічні функції
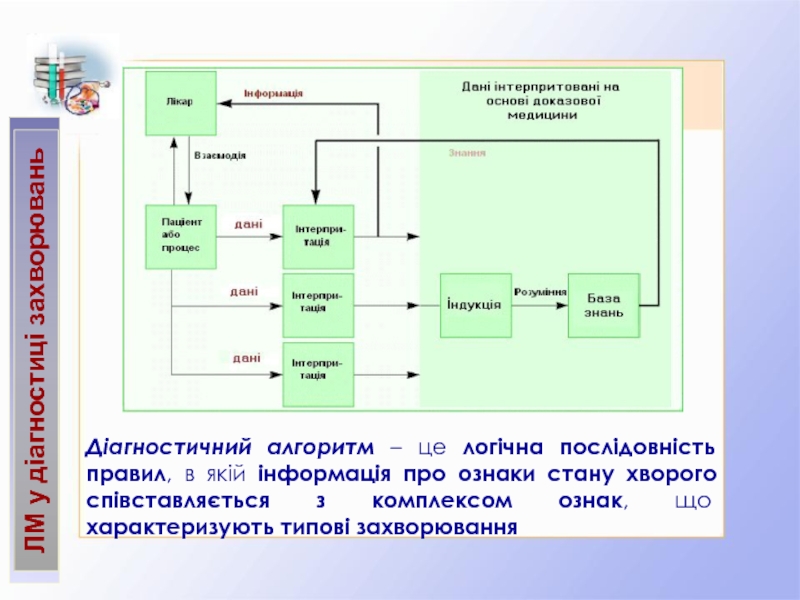
Логічні моделі у діагностиці захворювань
3.1. Типи діагностичних і прогностичних технологій
3.2. Види лікарської логіки

П л а н л е к ц і ї

чи хибне.
Висловлювання позначають буквами латинського алфавіту: А, В, X тощо.
Наприклад,

А: у пацієнта спостерігається порушення серцевого ритму

Висловлювання

Речення

?

існуючий світ
Просте висловлювання
Складене висловлювання
утворюється з простих висловлювань за допомо-гою

логічних операторів

Листя м’яти містить ефірну олію

Валідол справляє седа-тивну і судинорозши-рювальну дію

з певним ступенем припущення
Проблемне висловлювання
Достовірне висловлювання
висловлювання, що містить знання,

обґрунтовані та перевірені практикою

Умовне висловлювання

висловлювання, в якому ві-дображається залежність того чи іншого явища від тих чи інших обставин

причиною головного болю є, ймовірно, підвищений тиск

життя без води неможливе

якщо в організмі не вистачає вітаміну D, то існує велика ймовірність розвитку рахіту

випадку воно називається істинним, у другому − хибним.
Множина значень

висловлювання

Істинне

1

І

Хибне

0

Х

Пневмонія − запалення легень

А

= 1

А: Пневмонія − запалення легень

засоби (алфавіт логіки висловлювань): - змінні логіки висловлювань – A, B,

C, D, … позначають прості висловлювання; - знаки логічних сполучників: ∧ – кон’юнкція; ∨ – диз’юнкція; → – імплікація; ↔ – еквіваленція; ¬ – заперечення; - технічні знаки: дужки, кома.

Алфавіт висловлювання

логічну змінну
Бінарні
оператори, що використовують дві логічні змінні

істинне, коли А – хибне і хибне, коли А –

істинне.

Логічні операції

Таблиця істинності для заперечення

А ∧ В , яке істинне тоді і тільки тоді,

коли істині висловлення А і В.

Логічні операції

Таблиця істинності для кон’юнкції

A ∨ B , яке хибне тоді і тільки тоді,

коли хибні висловлення А і В.

Логічні операції

Таблиця істинності для диз’юнкції

A→B , яке є хибним лише тоді, коли антецедент (перша

частина імплікації – висловлення А) є істинним, а консеквент (друга частина імплікації – висловлення В) – хибним.

Логічні операції

Таблиця істинності для імплікації

таке висловлення А↔В , яке є істинним тоді і тільки

тоді, коли висловлення А і В одночасно істинні або хибні

Логічні операції

Таблиця істинності для еквівалентності

основні

тіла (шкіри), сильний біль в ділянці тазу, неможливість самостійно встати

або сісти”

А − “наявність ушкодження зовнішніх тканин”;
В – “сильний біль в ділянці тазу”;
С – “неможливість самостійно встати”;
К − “неможливість самостійно сісти”;
1 – відкритий перелом тазу;

(А ∧ В ∧ (С∨К)) = 1

в якій інформація про ознаки стану хворого співставляється з комплексом

ознак, що характеризують типові захворювання

здійснює виконання алгоритму, тобто чіткої послідовності заздалегідь заданих дій і

правил ⇒ лікар повинен мати готове (і в ідеалі – єдине) діагностичне рішення, а також − первинну схему лікувального процесу

гепатиту
І. Якщо колір шкіри пацієнта має жовтий відтінок, то необхідно

переконатися, що жовтуха не механічна. Пальпацією необхідно визначити збільшення і хворобливість печінки. Рентгенографічно необхідно виключити пухлину голівки підшлункової залози і закупорювання жовчних проток. ІІ. Якщо жовтуха паренхіматозна, необхідно переконатися, що ураження печінкової тканини має запальний характер. Необхідно виявити: - підвищені значення ШОЕ і лейкоцитів крові (ознаки запалення); - підвищення рівня амінотрансфераз: АЛТ і ACT (вихід ферментів у кров − ознака руйнування гепатоцитів).

кількості патологій;
спроби створення універсальних алгоритмів призводять до їх якісного ускладнення,

до ступеня практичного невиконання їх в особі одного лікаря

Недоліки детерміністичної логіки

ЛМ у діагностиці захворювань

цілих етапів діагностичного процесу з економією робочого часу лікаря.
Переваги детерміністичної

логіки

ЛМ у діагностиці захворювань

захворювання ознак (симптомів), які складають типовий комплекс симптомів даного захворювання.

2. Позначення наявності симптому як 1, а відсутності – 0. 3. Розгляд різних комбінацій симптомів для даного діагнозу. 4. Складення таблиці (матриці), яка відображає зв’язок “симптоми – хвороби”.