Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
GCSE Circle Theorems
Содержание
- 1. GCSE Circle Theorems
- 2. Sector(Minor)SegmentDiameterRadiusTangentChord(Minor) ArcCircumference?????!???
- 3. Circle Theorems are laws that apply to
- 4. !radiustangent“Angle between radius and tangent is 90”.“Angle
- 5. !“Angles in same segment are equal.”“Angle at centre is twice the angle at the circumference.”
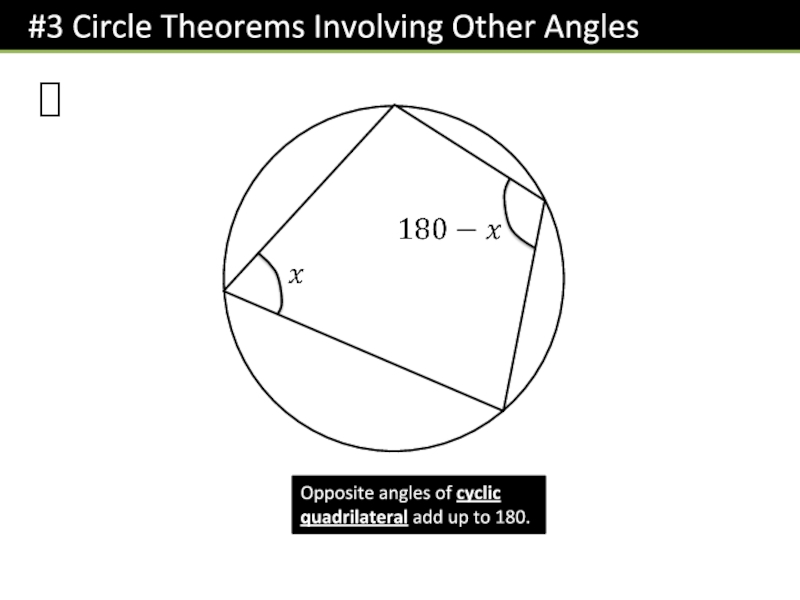
- 6. !Opposite angles of cyclic quadrilateral add up to 180.
- 7. Lengths of the tangents from a point to the circle are equal.
- 8. Radius is of constant lengthBro Tip: When
- 9. Identify which circle theorems you could use
- 10. Identify which circle theorems you could use
- 11. Identify which circle theorems you could use
- 12. Identify which circle theorems you could use
- 13. Identify which circle theorems you could use
- 14. Identify which circle theorems you could use
- 15. ??
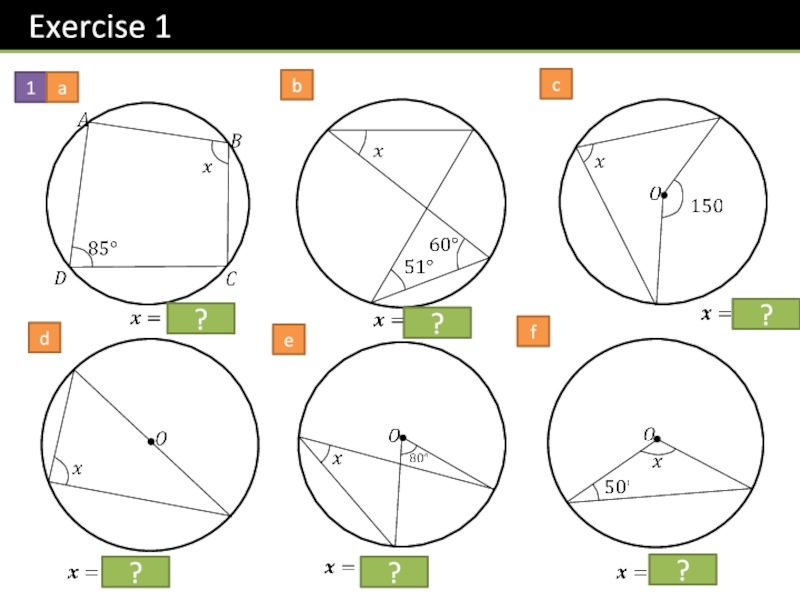
- 16. 1bcadef??????
- 17. 2abcde?????
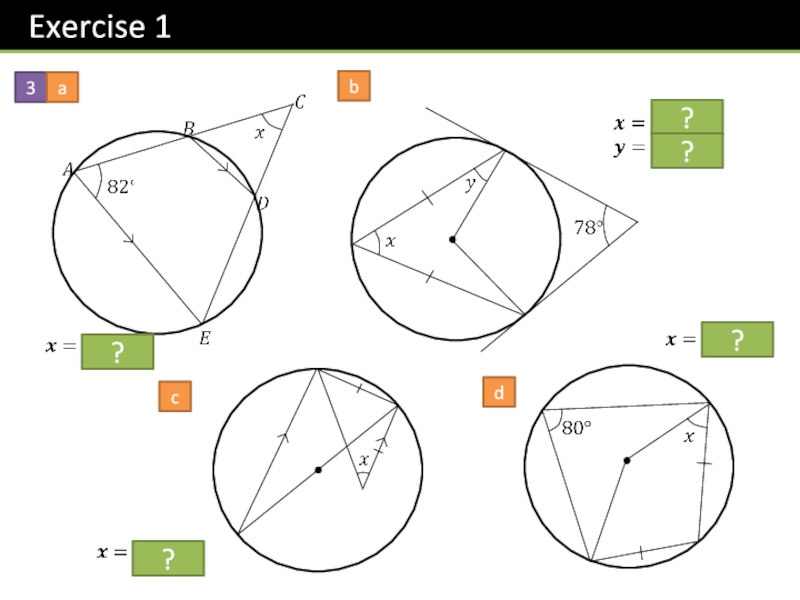
- 18. 3abcd?????
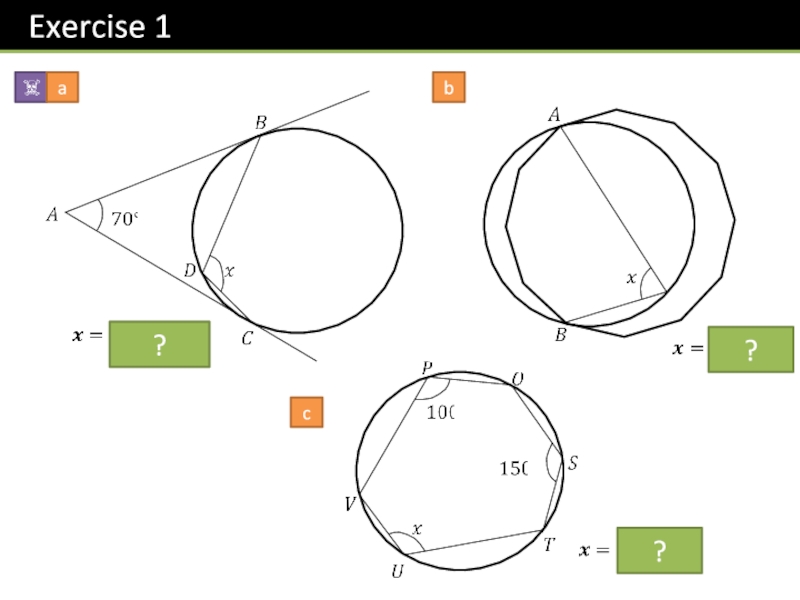
- 19. 4???
- 20. Nabc???
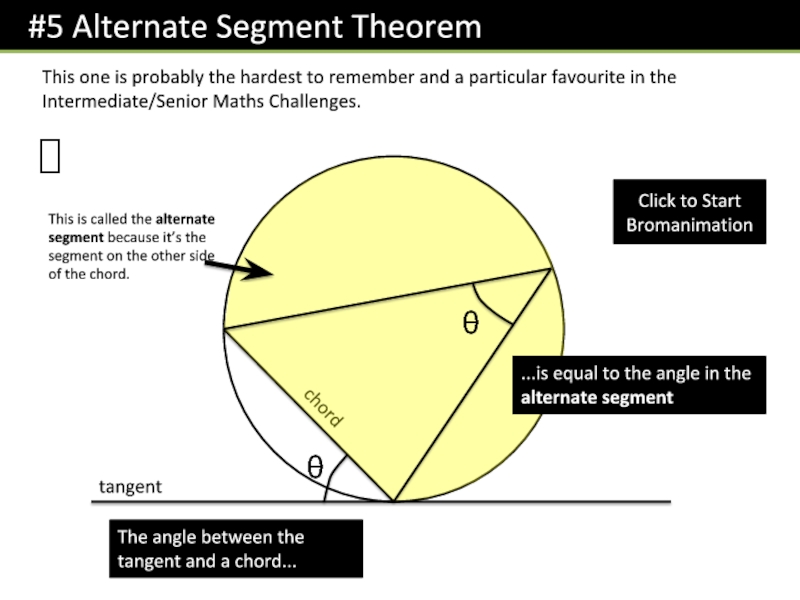
- 21. This one is probably the hardest to
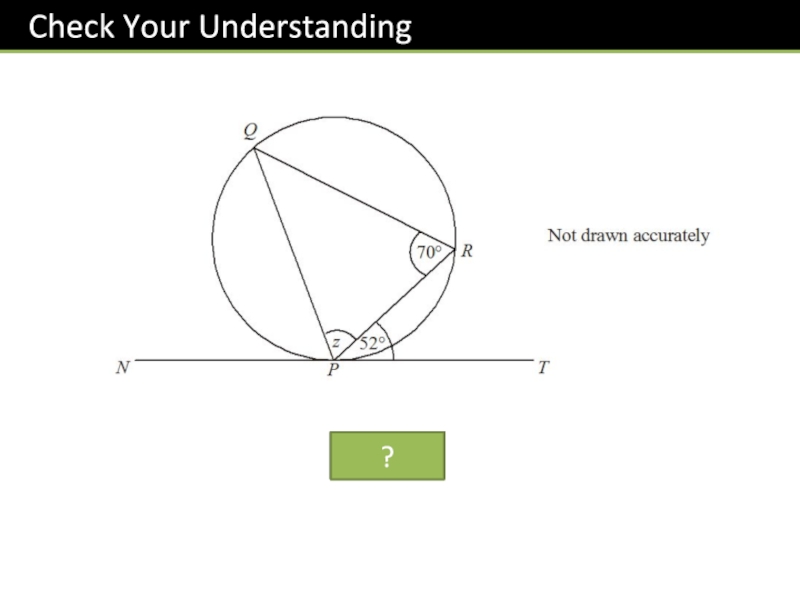
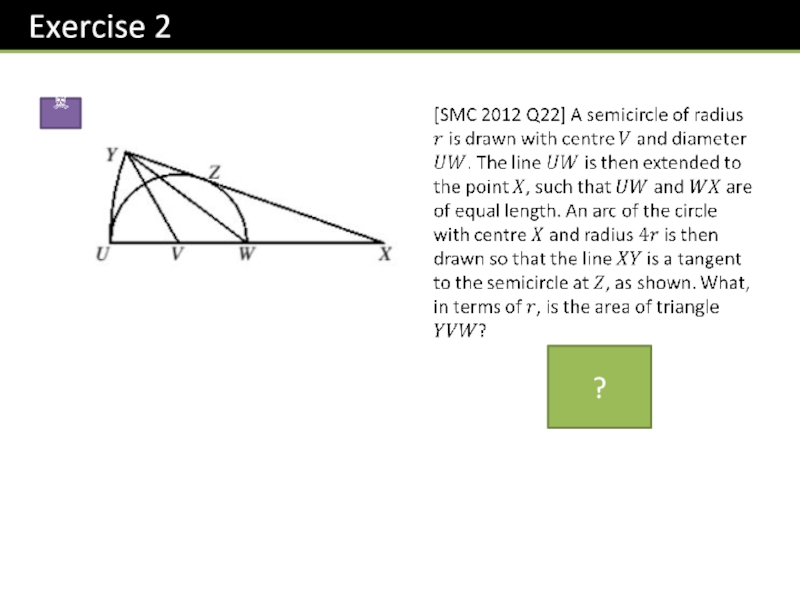
- 22. z = 58?
- 23. Angle ABC = Give a reason:Angle AOC
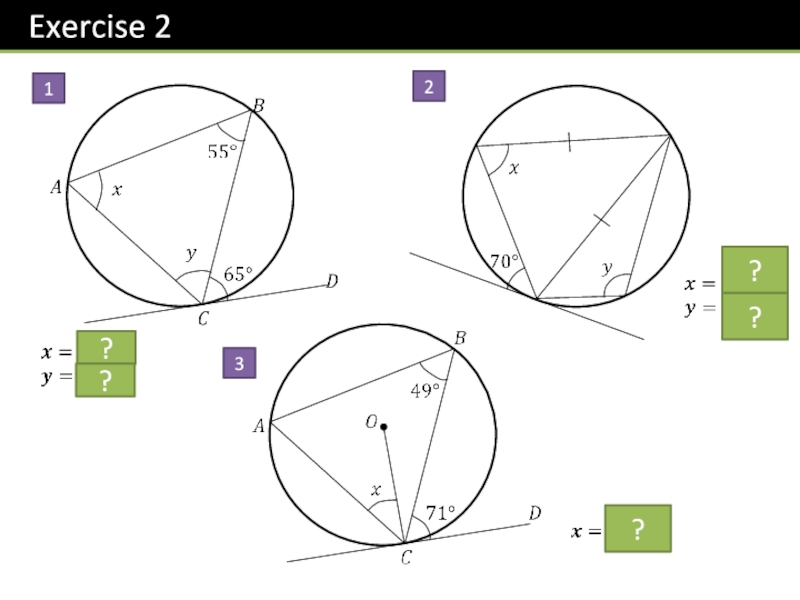
- 24. 123?????
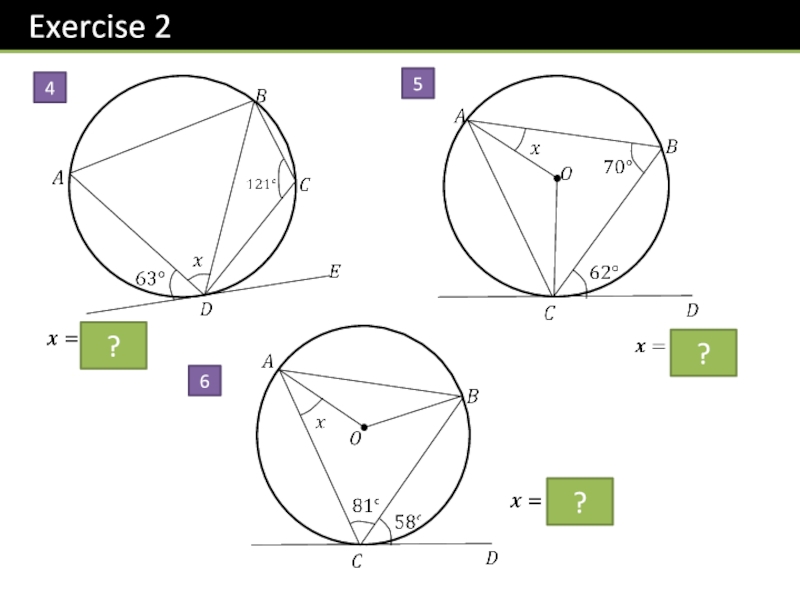
- 25. 456???
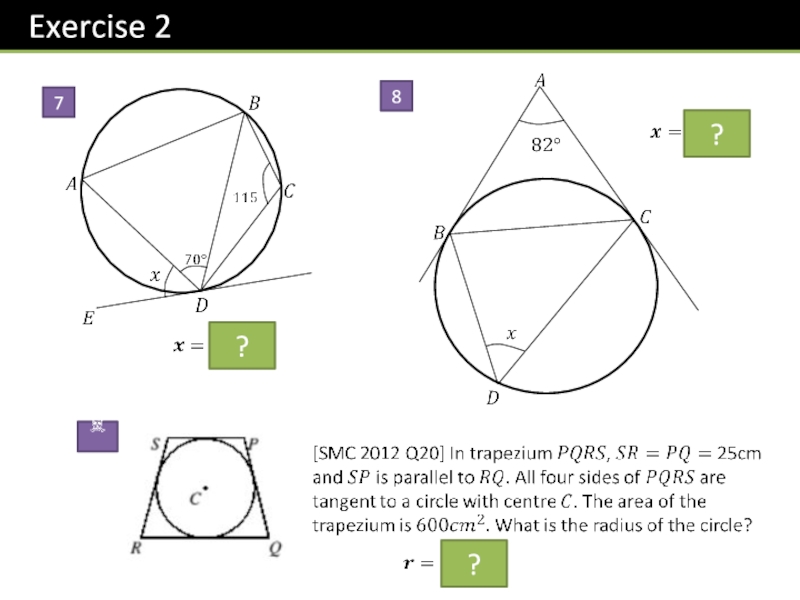
- 26. 78N1???
- 27. N2?
- 28. ABCOaa180-2a2a90-a90-aLet angle BAO be a. Triangle ABO
- 29. !xabba??Opposite angles of cyclic quadrilateral add up
- 30. Alternate Segment Theorem1: Angle between tangent and
- 31. Скачать презентанцию
Слайды и текст этой презентации
Слайд 1GCSE Circle Theorems
Dr J Frost (jfrost@tiffin.kingston.sch.uk)
www.drfrostmaths.com
Last modified: 20th November
2016
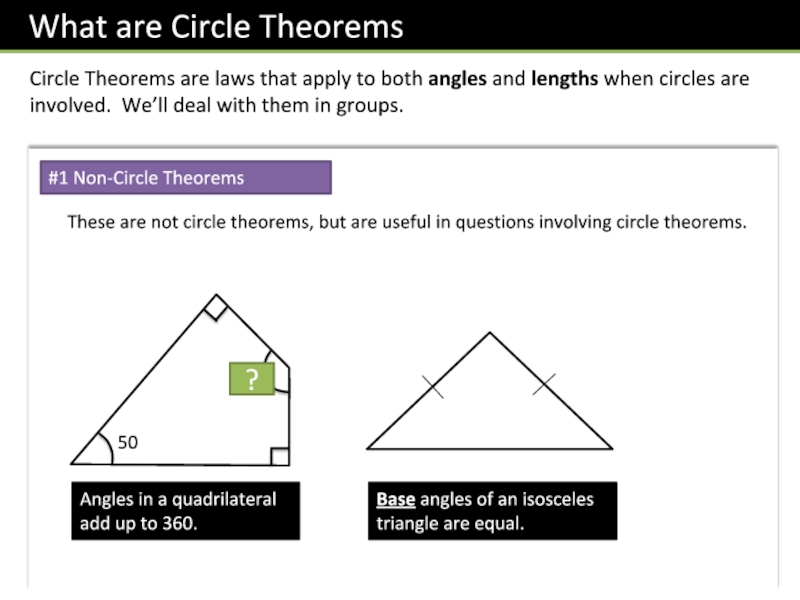
Слайд 3Circle Theorems are laws that apply to both angles and
lengths when circles are involved. We’ll deal with them in
groups.#1 Non-Circle Theorems
These are not circle theorems, but are useful in questions involving circle theorems.
50
130
?
Angles in a quadrilateral add up to 360.
Base angles of an isosceles triangle are equal.
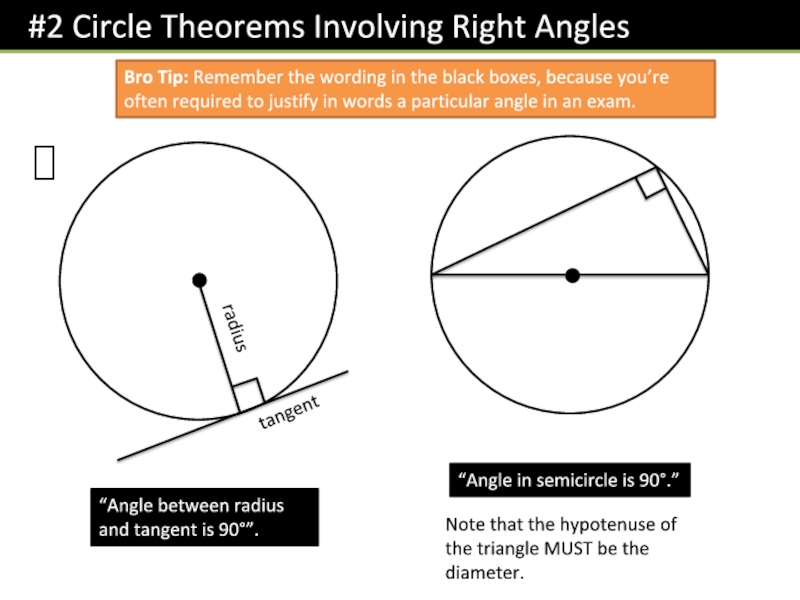
Слайд 4!
radius
tangent
“Angle between radius and tangent is 90”.
“Angle in semicircle is
90.”
Note that the hypotenuse of the triangle MUST be the
diameter.Bro Tip: Remember the wording in the black boxes, because you’re often required to justify in words a particular angle in an exam.
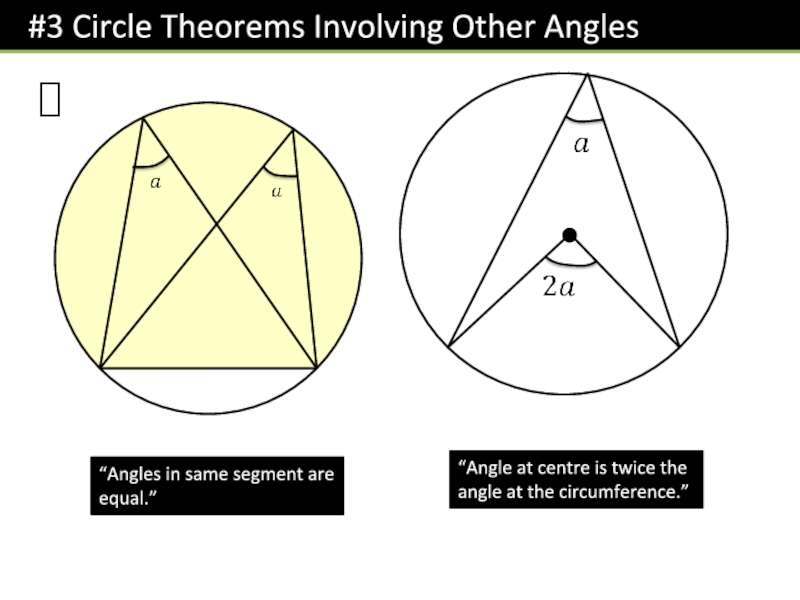
Слайд 5!
“Angles in same segment are equal.”
“Angle at centre is twice
the angle at the circumference.”
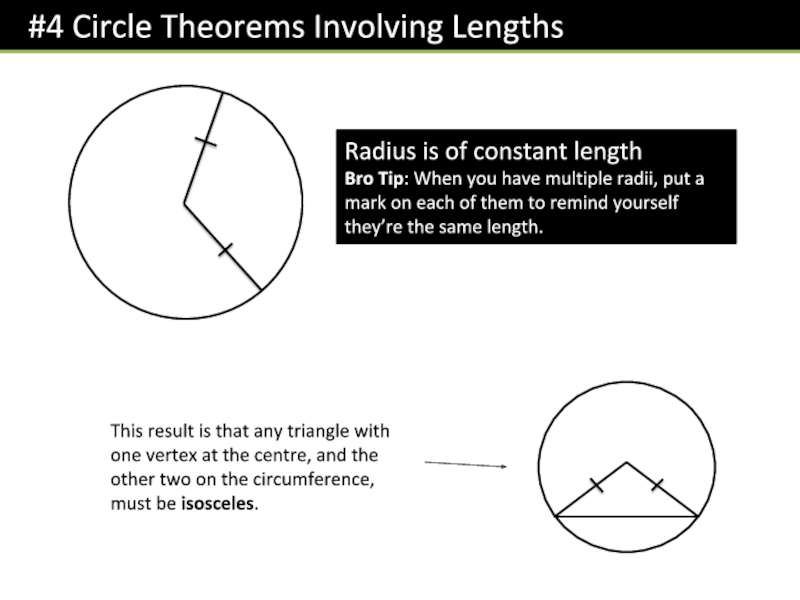
Слайд 8Radius is of constant length
Bro Tip: When you have multiple
radii, put a mark on each of them to remind
yourself they’re the same length.This result is that any triangle with one vertex at the centre, and the other two on the circumference, must be isosceles.
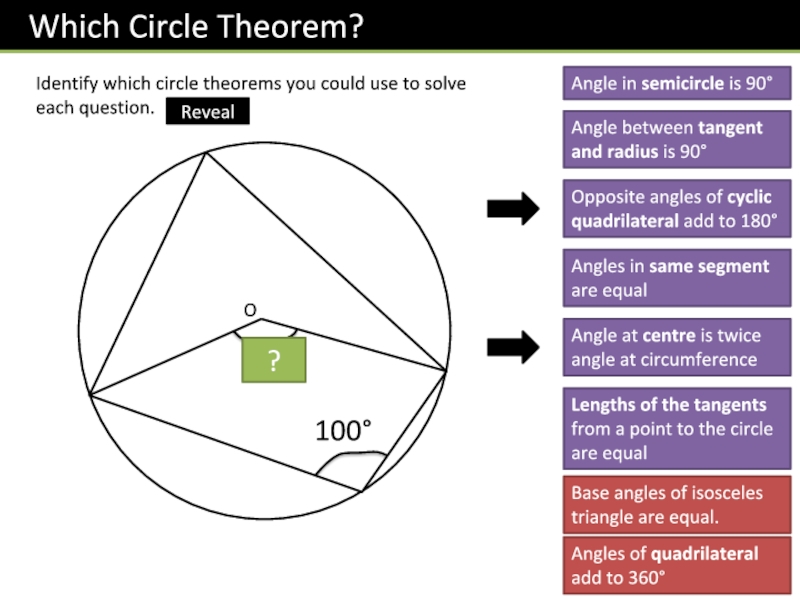
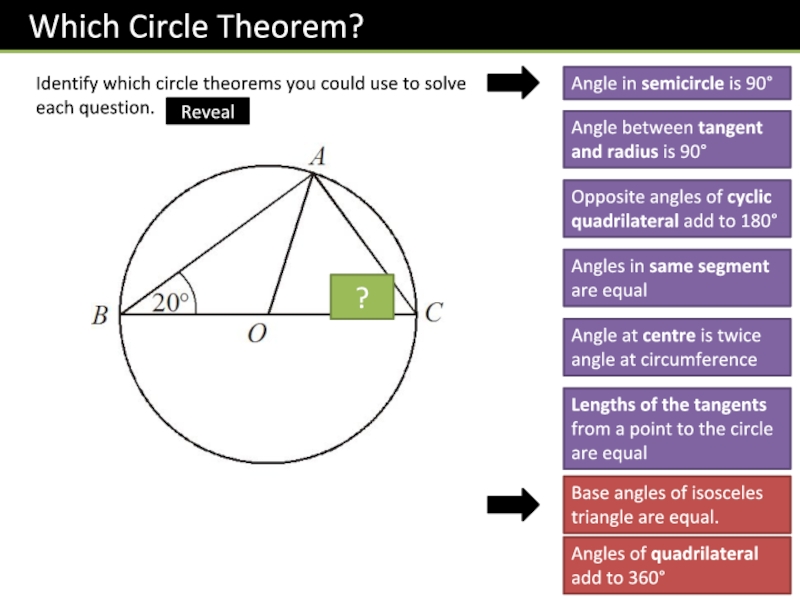
Слайд 9Identify which circle theorems you could use to solve each
question.
O
160
100
?
Angle in semicircle is 90
Angle between tangent and radius is
90Opposite angles of cyclic quadrilateral add to 180
Angles in same segment are equal
Angle at centre is twice angle at circumference
Lengths of the tangents from a point to the circle are equal
Base angles of isosceles triangle are equal.
Angles of quadrilateral add to 360
Reveal
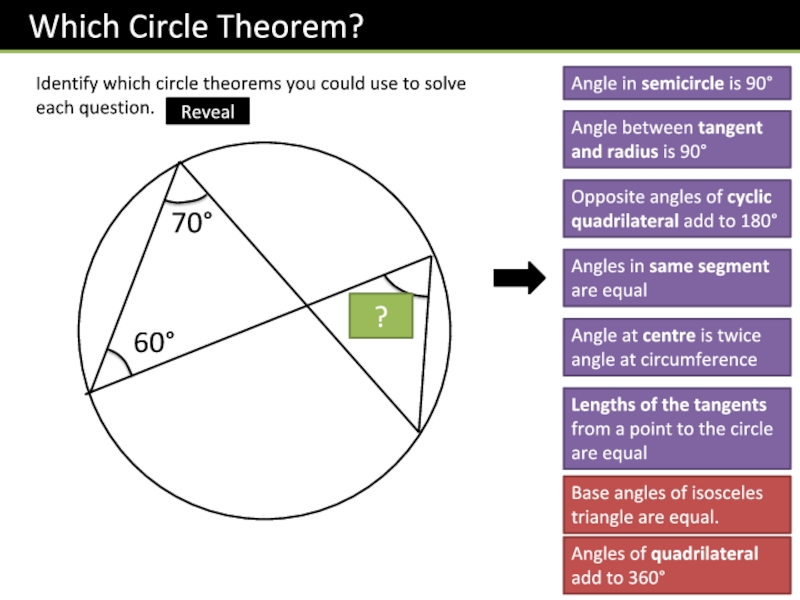
Слайд 10Identify which circle theorems you could use to solve each
question.
70
60
70
?
Angle in semicircle is 90
Angle between tangent and radius is
90Opposite angles of cyclic quadrilateral add to 180
Angles in same segment are equal
Angle at centre is twice angle at circumference
Lengths of the tangents from a point to the circle are equal
Base angles of isosceles triangle are equal.
Angles of quadrilateral add to 360
Reveal
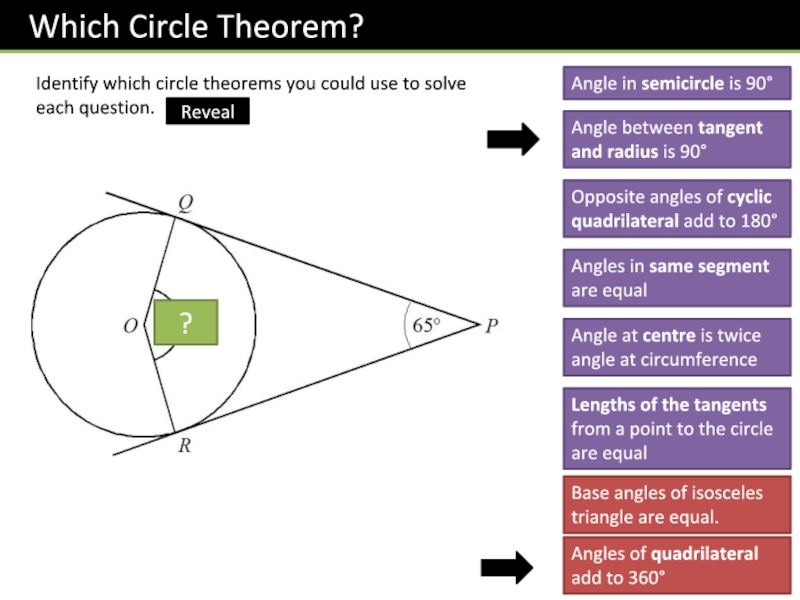
Слайд 11Identify which circle theorems you could use to solve each
question.
115
?
Angle in semicircle is 90
Angle between tangent and radius is
90Opposite angles of cyclic quadrilateral add to 180
Angles in same segment are equal
Angle at centre is twice angle at circumference
Lengths of the tangents from a point to the circle are equal
Base angles of isosceles triangle are equal.
Angles of quadrilateral add to 360
Reveal
Слайд 12Identify which circle theorems you could use to solve each
question.
70
?
Angle in semicircle is 90
Angle between tangent and radius is
90Opposite angles of cyclic quadrilateral add to 180
Angles in same segment are equal
Angle at centre is twice angle at circumference
Lengths of the tangents from a point to the circle are equal
Base angles of isosceles triangle are equal.
Angles of quadrilateral add to 360
Reveal
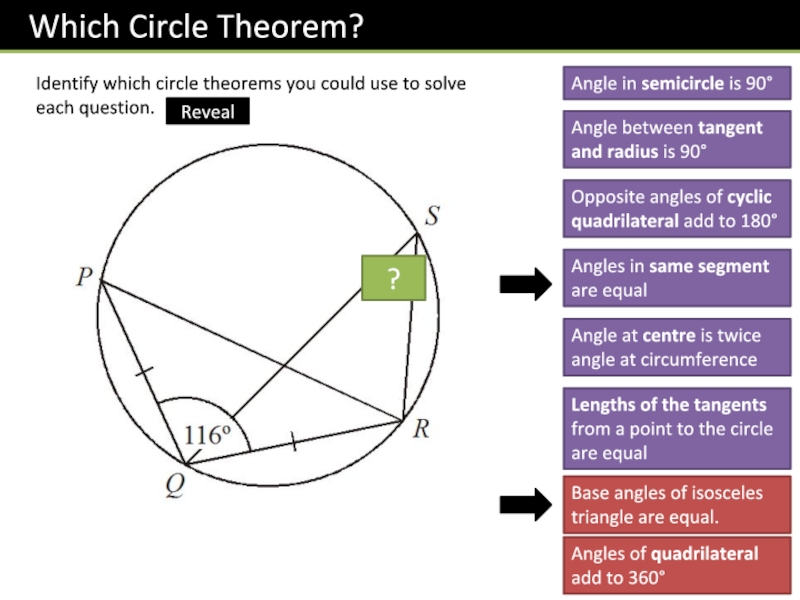
Слайд 13Identify which circle theorems you could use to solve each
question.
Angle in semicircle is 90
Angle between tangent and radius is
90Opposite angles of cyclic quadrilateral add to 180
Angles in same segment are equal
Angle at centre is twice angle at circumference
Lengths of the tangents from a point to the circle are equal
32
?
Base angles of isosceles triangle are equal.
Angles of quadrilateral add to 360
Reveal
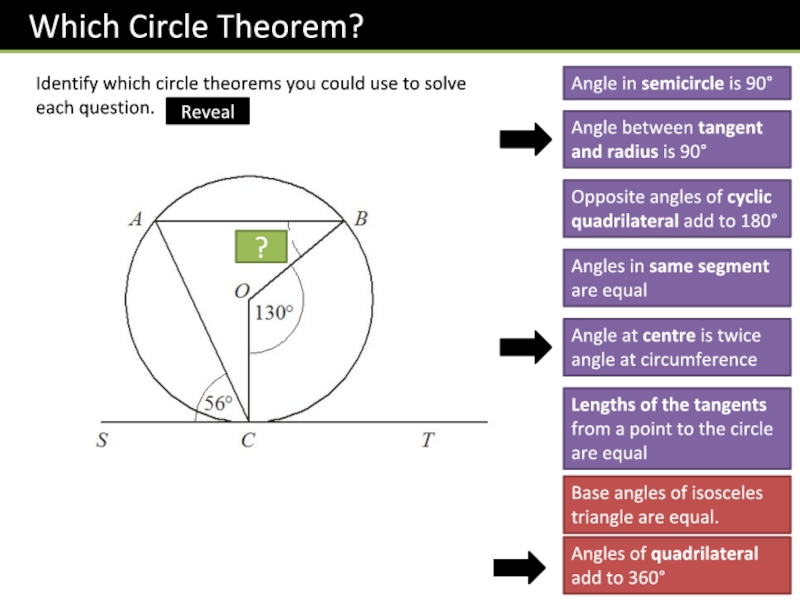
Слайд 14Identify which circle theorems you could use to solve each
question.
Angle in semicircle is 90
Angle between tangent and radius is
90Opposite angles of cyclic quadrilateral add to 180
Angles in same segment are equal
Angle at centre is twice angle at circumference
Lengths of the tangents from a point to the circle are equal
31
?
Base angles of isosceles triangle are equal.
Angles of quadrilateral add to 360
Reveal
Слайд 21This one is probably the hardest to remember and a
particular favourite in the Intermediate/Senior Maths Challenges.
!
The angle between the
tangent and a chord...Click to Start Bromanimation
...is equal to the angle in the alternate segment
Слайд 23Angle ABC =
Give a reason:
Angle AOC =
Give a
reason:
Angle CAE =
Give a reason:
112
Supplementary angles of cyclic quadrilateral
add up to 180.136
68
Angle at centre is double angle at circumference.
Alternate Segment Theorem.
?
?
?
?
?
?
Source: IGCSE Jan 2014 (R)
Слайд 28A
B
C
O
a
a
180-2a
2a
90-a
90-a
Let angle BAO be a. Triangle ABO is isosceles so
ABO = a. Remaining angle in triangle must be 180-2a.
Thus BOC = 2a. Since triangle BOC is isosceles, angle BOC = OCB = 90 – a. Thus angle ABC = ABO + OBC = a + 90 – a = 90.?
?
?
?
?
Слайд 29!
x
a
b
b
a
?
?
Opposite angles of cyclic quadrilateral add up to 180.
This combined
angle
= 180 – a – b
(angles in a
triangle)?
Adding opposite angles:
a + b + 180
– a – b = 180
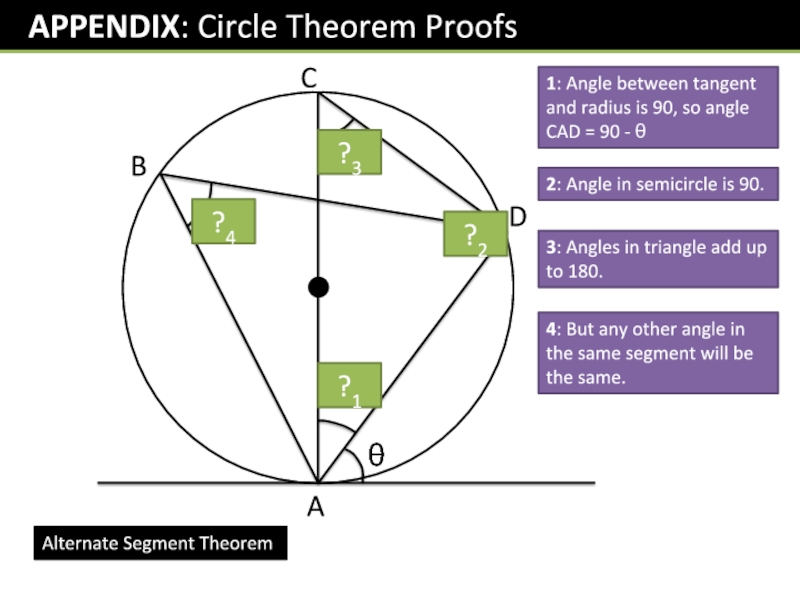
Слайд 30Alternate Segment Theorem
1: Angle between tangent and radius is 90,
so angle CAD = 90 -
90-
A
B
C
D
?1
?3
?2
2: Angle in semicircle
is 90.3: Angles in triangle add up to 180.
?4
4: But any other angle in the same segment will be the same.