Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Географический факультет Московского государственного университета им
Содержание
- 1. Географический факультет Московского государственного университета им
- 2. Современное ландшафтоведение – комплексная физико-географическая наука о
- 3. Направления исследования ландшафтоведения [К.Н.Дьяконов, 2004]структурно-генетическоеструктурно-функциональноефункционально-динамическое геофизическоегеохимическоесоциальный ландшафтогенезпалеоландшафтноеландшафтная экологияландшафтное
- 4. ЦЕЛЬ КУРСА охарактеризовать физико-математический подход как
- 5. наиболее важные методологические принципы (регулятивы) научной теории:принципиальная
- 6. развитие моделирования (на примере речного стока), в
- 7. Основные предпосылки создания физико-математической теории геосистем •
- 8. Геосистемы – открытые иерархически организованные динамические системы,
- 9. ЭТАПЫ РАЗРАБОТКИ ТЕОРИИ ГЕОСИСТЕМ1.Систематизация структурообразующих геосистемных процессов2.Формализация
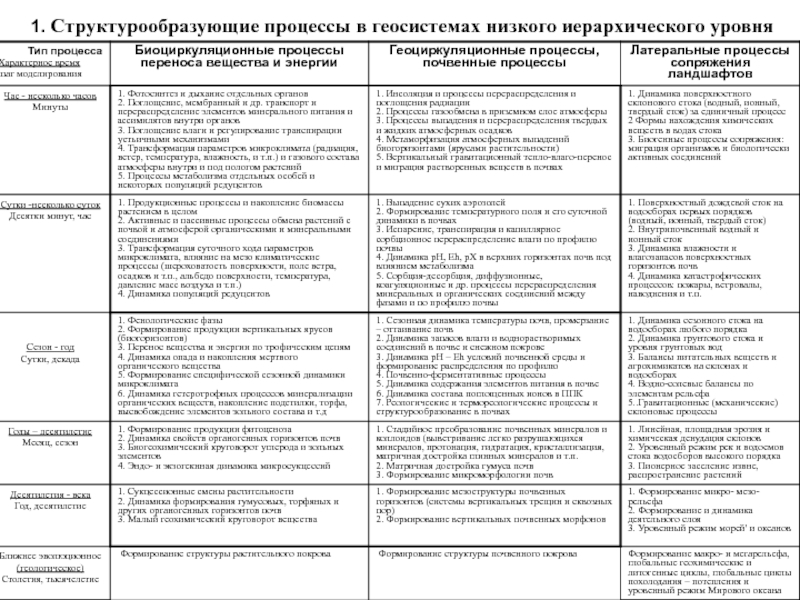
- 10. 1. Структурообразующие процессы в геосистемах низкого иерархического уровня
- 11. ВЫБОР ПАРАМЕТРОВ ЭТО ВВЕДЕНИЕ АКСИОМАТИКИТ. о. природные
- 12. Основные геосистемные аксиомы и постулатыГеометрия пространства геосистем
- 13. Систематизация уровней почвенных структур по масштабной шкале [Шеин, 2005]
- 14. (х,t) - линейная плотность среды, ma,b –
- 15. Силовые поля и взаимодействияПроизводная импульса частицы во
- 16. Сплошная среда Исследование материальных тел - построение
- 17. Потенциальное силовое поле и градиент потенциала Работа
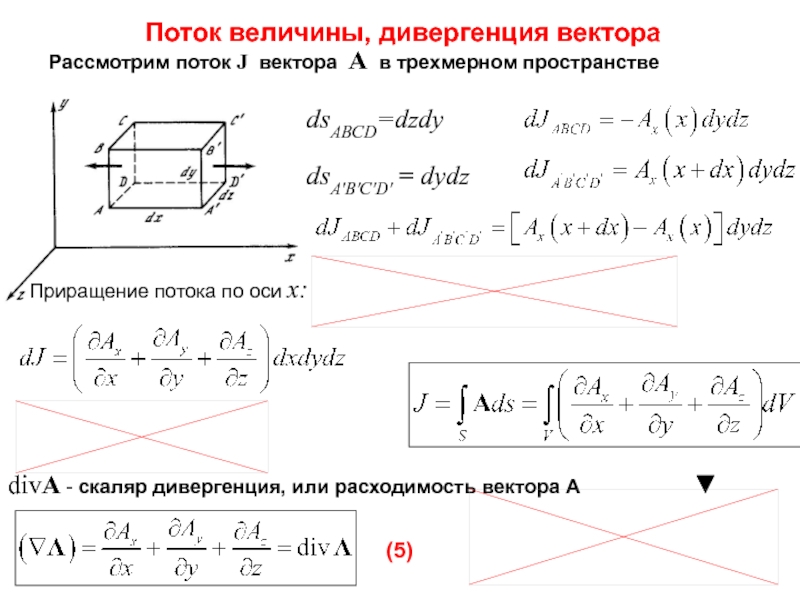
- 18. dsABCD=dzdy dsABCD = dydz divA - скаляр
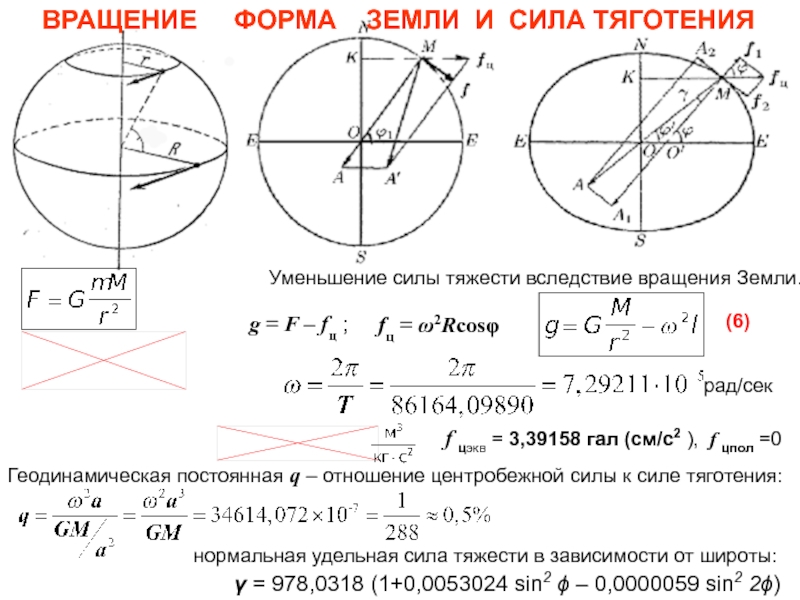
- 19. ВРАЩЕНИЕ ФОРМА ЗЕМЛИ И
- 20. Гравитационный потенциал частицы в поле гравитации
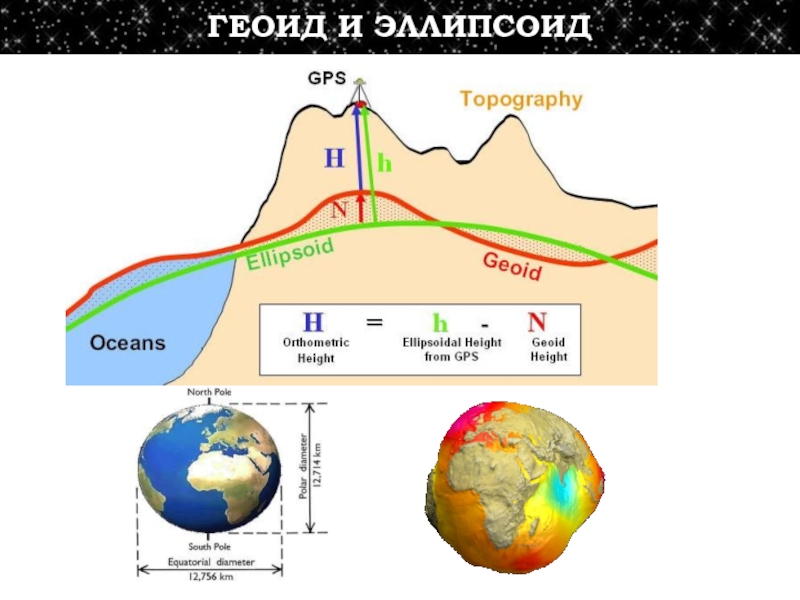
- 21. ГЕОИД И ЭЛЛИПСОИД
- 22. Слайд 22
- 23. Описание пространственной структуры геосистем
- 24. Классы морфометрических величин и понятий [Шарый, 1995]. 2. ВЫБОР ПАРАМЕТРОВ ПРОСТРАНСТВЕННОЙ СТРУКТУРЫ ГЕОСИСТЕМ
- 25. К понятиям В- и D-депрессий: две одинаковые
- 26. Формулы расчета локальных морфометрических величин [Shary, 1995]. ( p=z/x; q=z/y; r=2z/x2; s=2z/xy; t=2z/y2, z=z(x,y)).
- 27. КРУТИЗНА СКЛОНОВ G (slope steepness) – абсолютная
- 28. В точках поверхности h(x,y) определим вектор единичной
- 29. Поле высот z =z(х, у) и иллюстрация
- 30. Ориентация склонов, α (aspect) - азимут направления склона, отсчитываемый от северного направления по часовой стрелке
- 31. Цифровая модель рельефа (слева) и ориентации склонов (справа) южной части Центрального лесного государственного биосферного заповедника
- 32. Переходя к пределу при Δx->0, Δy->0 получаемds=Rd
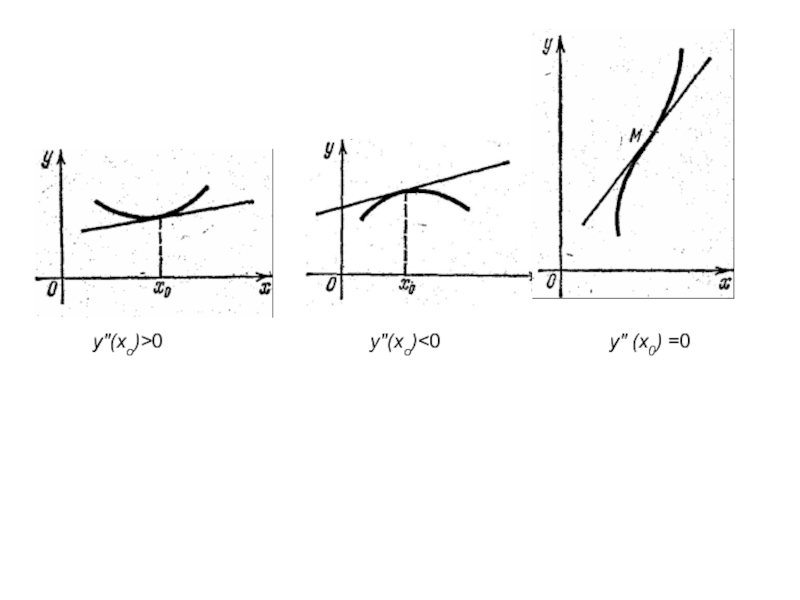
- 33. y"(xо)
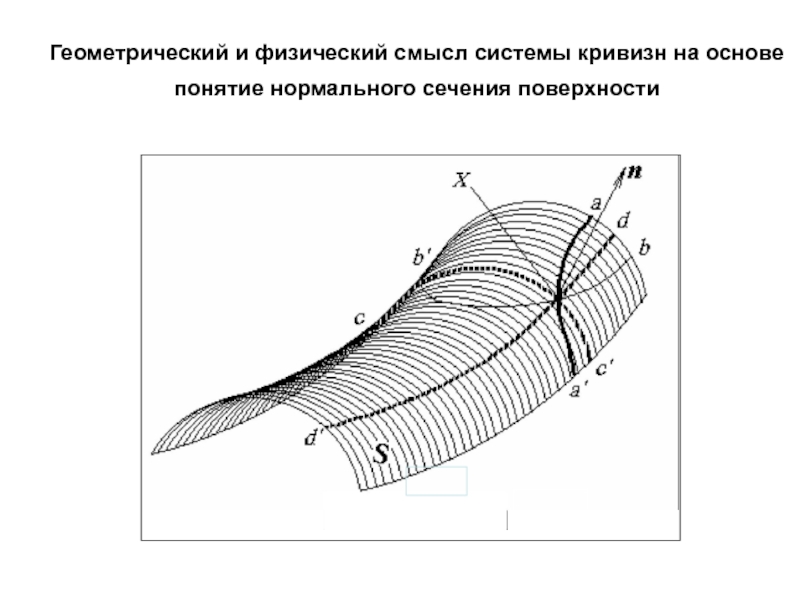
- 34. Геометрический и физический смысл системы кривизн на основе понятие нормального сечения поверхности
- 35. К ОПИСАНИЮ ДВУХ ОСНОВНЫХ МЕХАНИЗМОВ АККУМУЛЯЦИИ [ШАРЫЙ,1991].
- 36. Теорема: О первом механизме аккумуляции (Shary,1995)Для
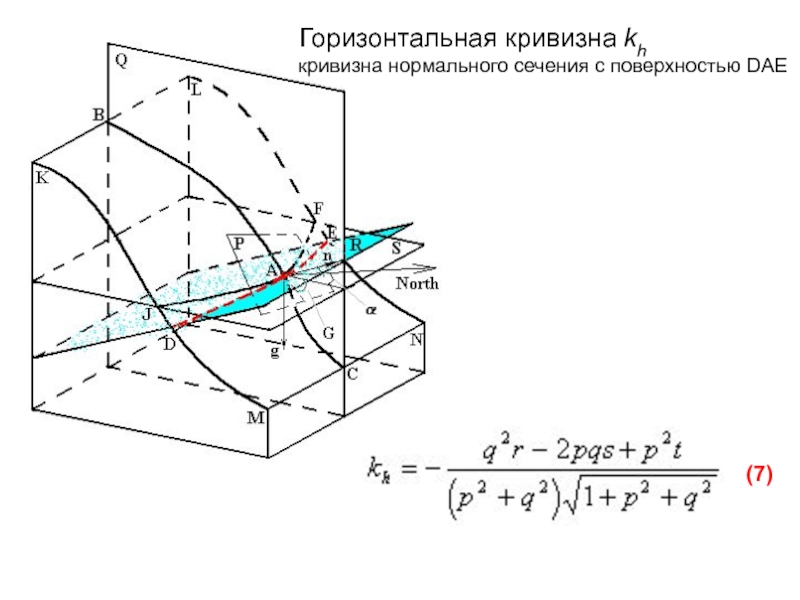
- 37. Горизонтальная кривизна kh кривизна нормального сечения с поверхностью DAE(7)
- 38. Теорема: О втором механизме аккумуляции. Для неособых
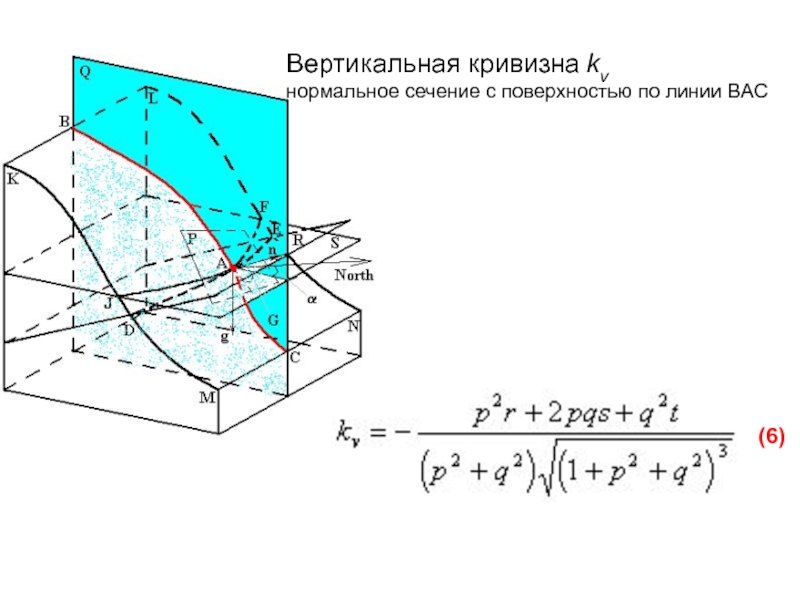
- 39. Вертикальная кривизна kv нормальное сечение с поверхностью по линии BAC (6)
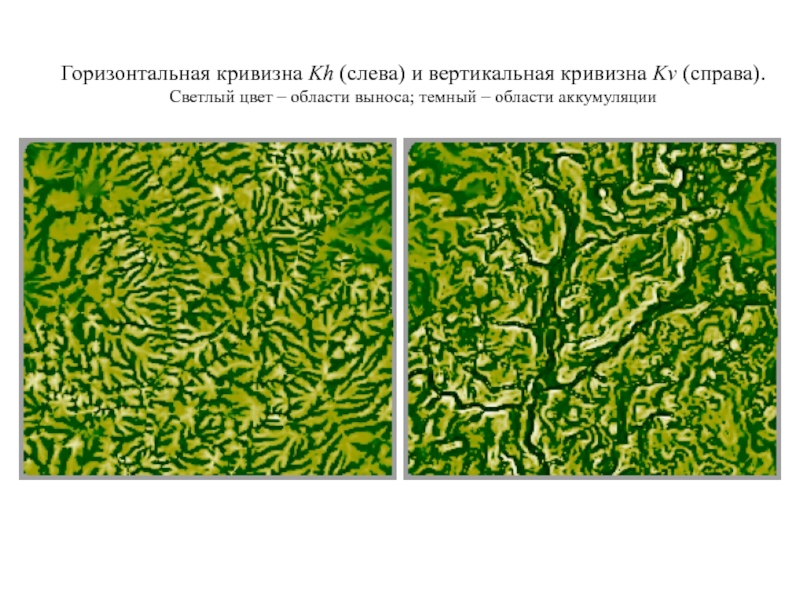
- 40. Горизонтальная кривизна Kh (слева) и вертикальная кривизна
- 41. Карта зон относительной аккумуляции и сноса (элементарных геосистем) леспаркхоза «Горки» в южной части Подмосковья.
- 42. Вероятные места обнаружения зоны аккумуляции показаны темным
- 43. Удельная площадь водосбора (слева) и дисперсивная площадь
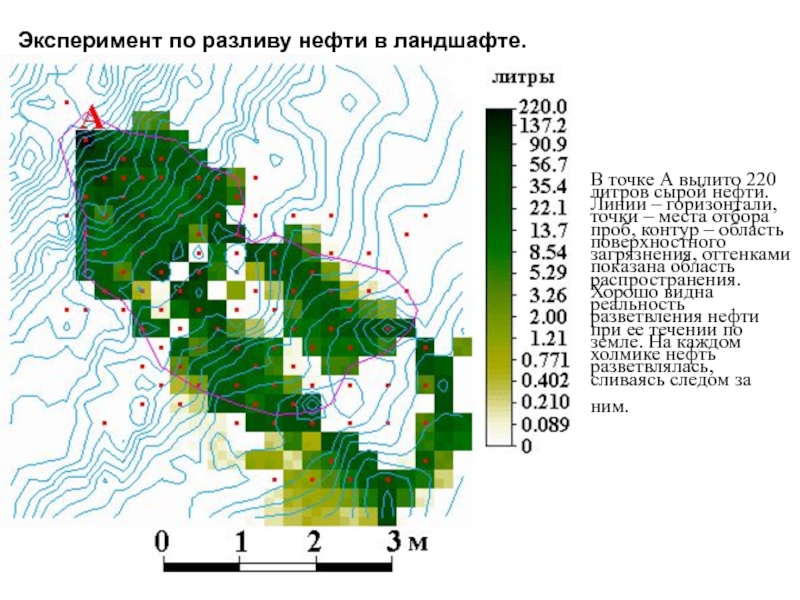
- 44. В точке А вылито 220 литров
- 45. Максимальное распространения нефти из разрыва трубопровода в
- 46. Верификация теоретических морфометрических величин по полевым данным
- 47. Верификация теоретических морфометрических величин по полевым данным
- 48. Морфометрическая дневная доза прямой солнечной радиации
- 49. 3. Общий алгоритм определения однородной территории по
- 50. Выбор и группировка морфометрических величин (МВ), описывающих
- 51. Морфометрические параметры рельефа Национального парка «Валдайский»: ориентация
- 52. Классификация поверхности рельефа ЦЛГПБЗ по параметрам перераспределения прямой солнечной радиации и тепла
- 53. Дифференциация поверхности рельефа по морфометрическим параметрам распределения солнечной радиации и тепла
- 54. Классификация поверхности рельефа по параметрам, характеризующим гидрологические условия. Проверка корректности методами дискриминантного анализа
- 55. Дифференциация рельефа по морфометрическим параметрам распределения гидрологического стока и заболачивания
- 56. Дифференциация рельефа по морфометрическим параметрам ландшафтно-геохимических механизмов переноса
- 57. Дифференциация рельефа по параметрам распределения геофизических полей.
- 58. Характеристический спектр зеленого листа в сравнении с
- 59. Физическая информация спектральных каналов съемки LANDSAT.1 канал
- 60. 4 канал (ближний инфракрасный):Связан со свойствами растительности.
- 61. Нормализованный разностный вегетационный индекс (Normalized Difference
- 62. Национальный парк «Валдайский», дихотомическая классификация съемки Landsat
- 63. Идентификация физического содержания классов растительного покрова НП
- 64. Значение натурных наблюдений в разработке теории геосистем1.
- 65. Суммы диаметров пород в типичных ландшафтах НП
- 66. Интерпретация физического содержания классов древостоев на основе полевых описаний:
- 67. Сопряженный профиль изменения гидрогеологических условий и продуктивности
- 68. Пространственная привязка линзы водонасыщенных флювиогляциальных песков, обнаруженной
- 69. Детализированные фрагменты радарограмм почв и четвертичных отложений
- 70. моренные гряды и камовые холмы с суглинистыми
- 71. Ландшафтная карта исследованной части национального парка «Валдайский».
- 72. 4. ФУНКЦИОНАЛЬНО-ДИНАМИЧЕСКАЯ КЛАССИФИКАЦИЯ ГЕОСИСТЕМФункциональный подход - выявление
- 73. Порядок водотоков по Хортону - СтралеруСогласно Роберту
- 74. Законы ХортонаЗакон продольных длин Хортона утверждает, что
- 75. Закон ТокунагаМодель Токунаги рассчитывает количество боковых притоков на реке одного порядка
- 76. Самоподобиебассейнов разногопорядка,выражающееся водинаковомсоотношенииплощадей бассейновразных порядковЗакон ХэкаОтношение длины основного водотока и его бассейна может быть выражено соотношением
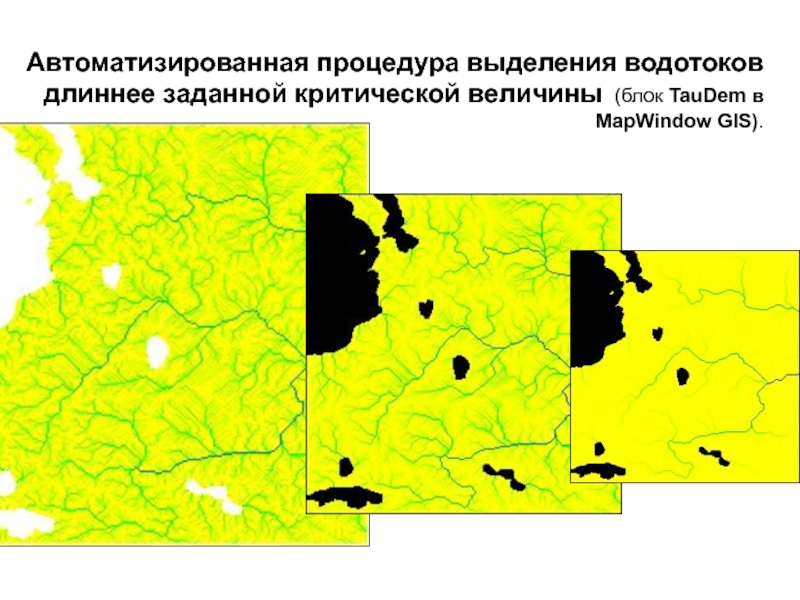
- 77. Автоматизированная процедура выделения водотоков длиннее заданной критической величины (блок TauDem в MapWindow GIS).
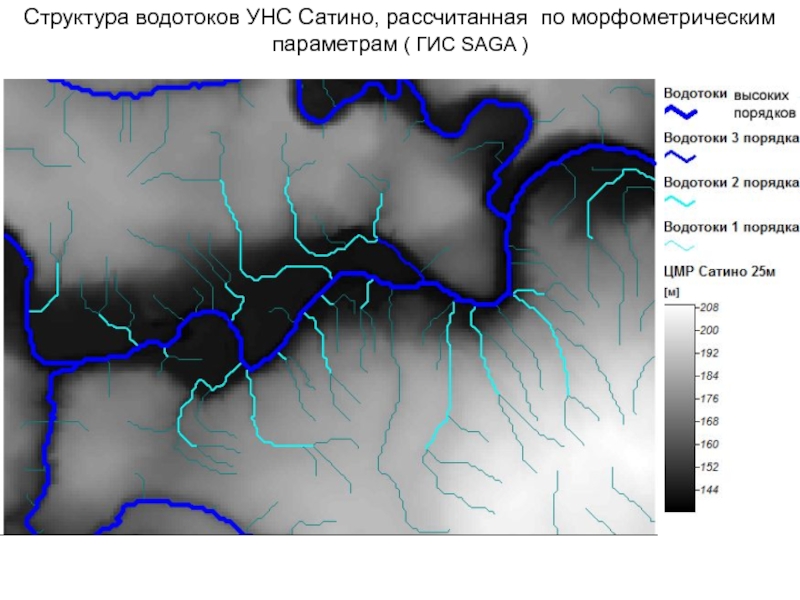
- 78. Структура водотоков УНС Сатино, рассчитанная по морфометрическим параметрам ( ГИС SAGA )
- 79. Критерии точности моделированияОшибки и доля верно отображённых
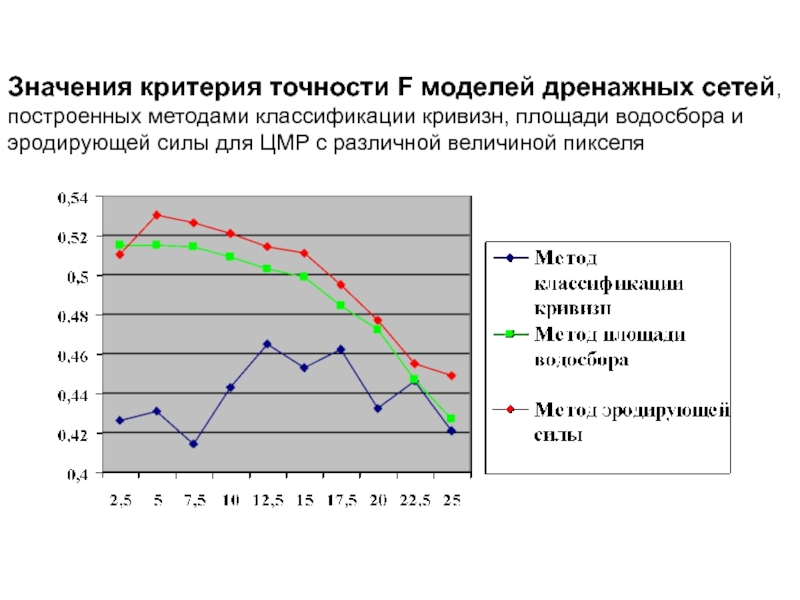
- 80. Значения критерия точности F моделей дренажных сетей,
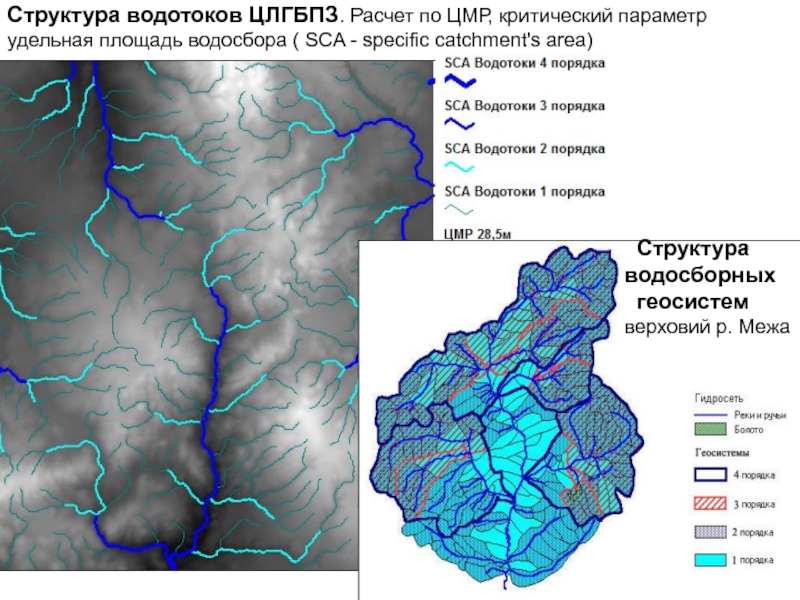
- 81. Структура водотоков ЦЛГБПЗ. Расчет по ЦМР, критический
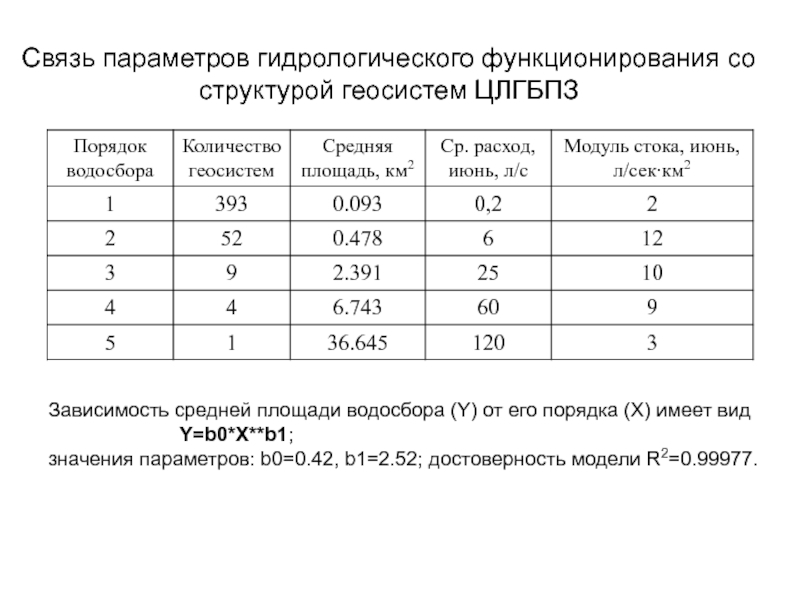
- 82. Связь параметров гидрологического функционирования со структурой геосистем
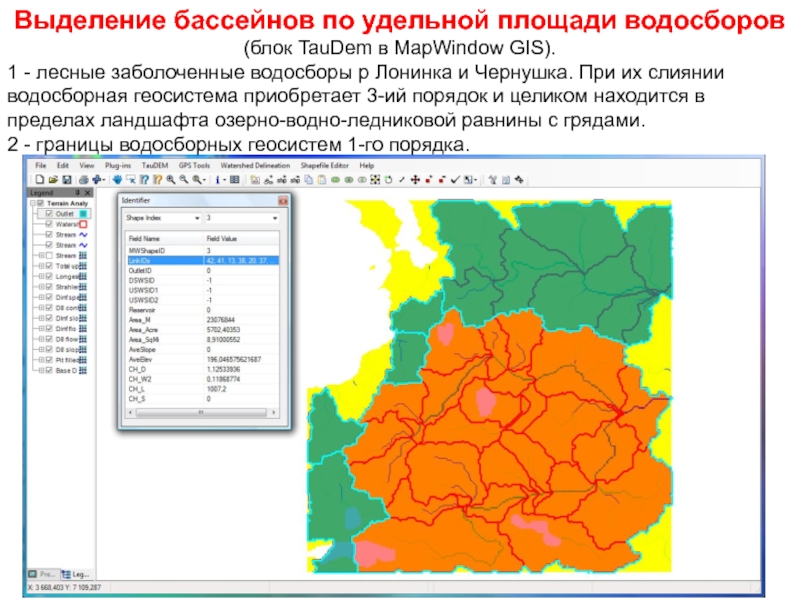
- 83. Выделение бассейнов по удельной площади водосборов (блок
- 84. Q – расход, м3/с; - площадь живого
- 85. Распределение гидрофизическихпараметров на основе структуры ландшафтов бассейна
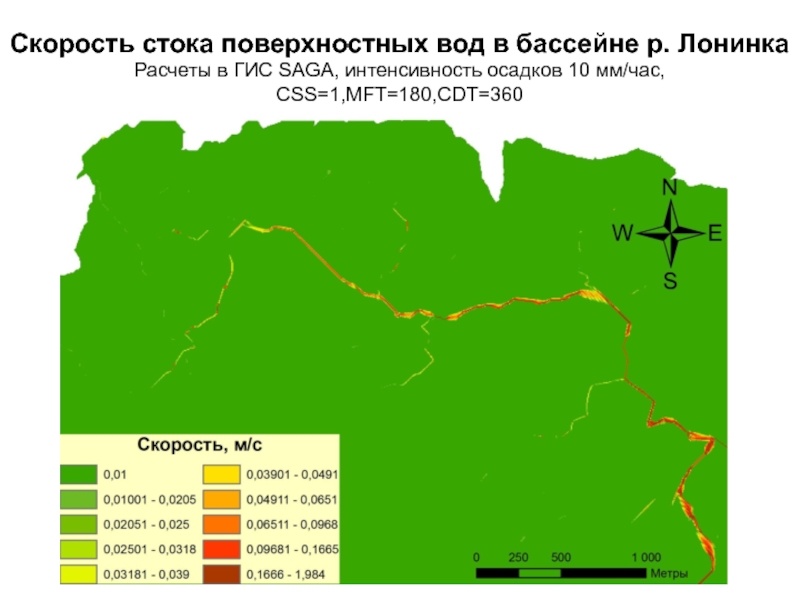
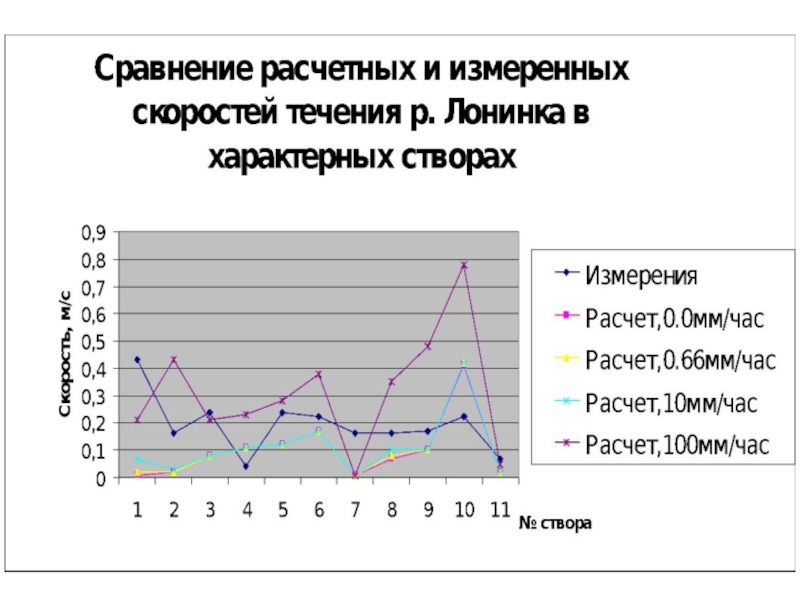
- 86. Скорость стока поверхностных вод в бассейне р.
- 87. Долина р. Лонинка в нижнем (слева) и в верхнем течении
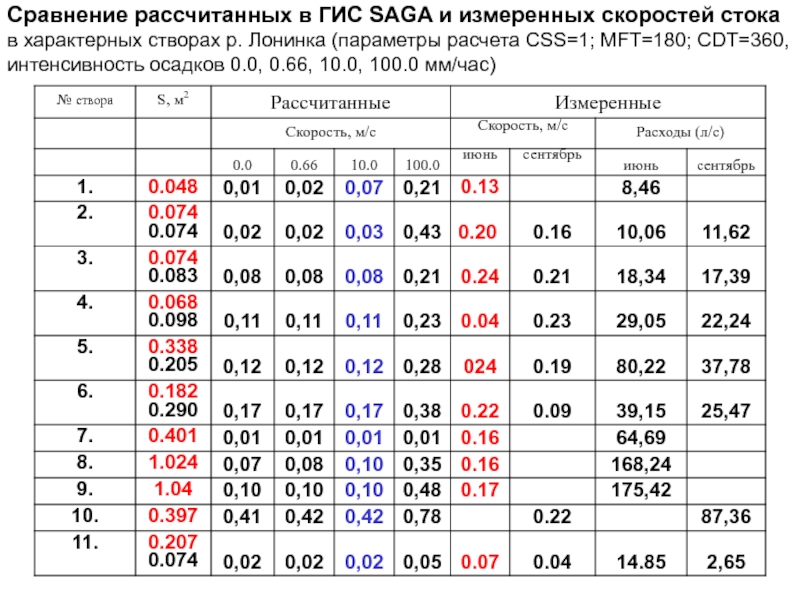
- 88. Сравнение рассчитанных в ГИС SAGA и измеренных
- 89. Слайд 89
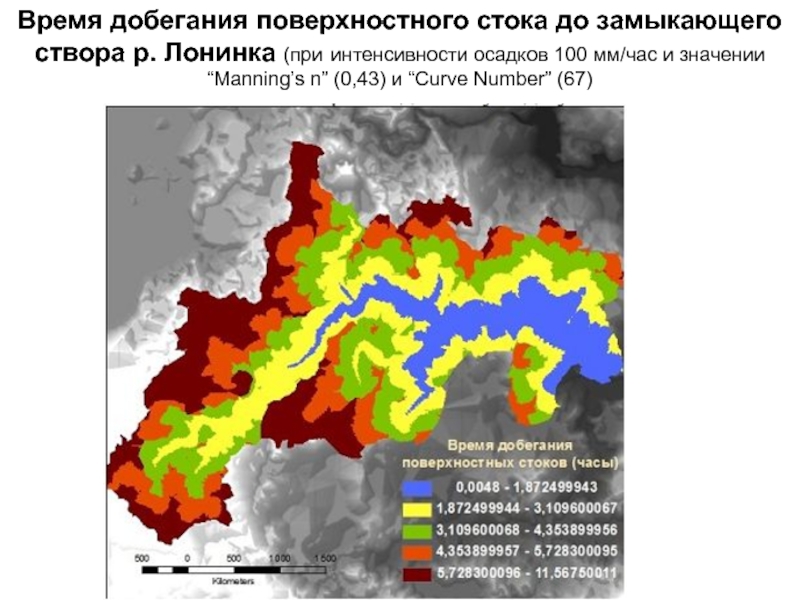
- 90. Время добегания поверхностного стока до замыкающего створа
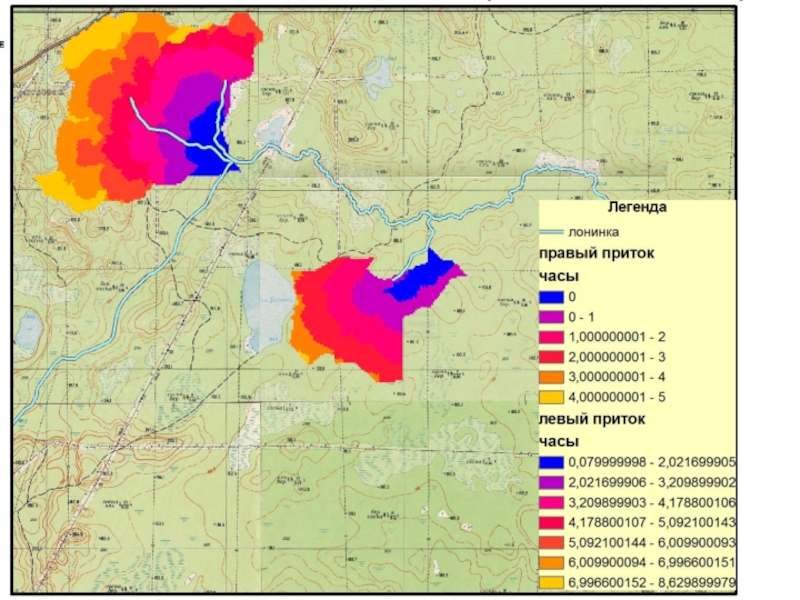
- 91. Слайд 91
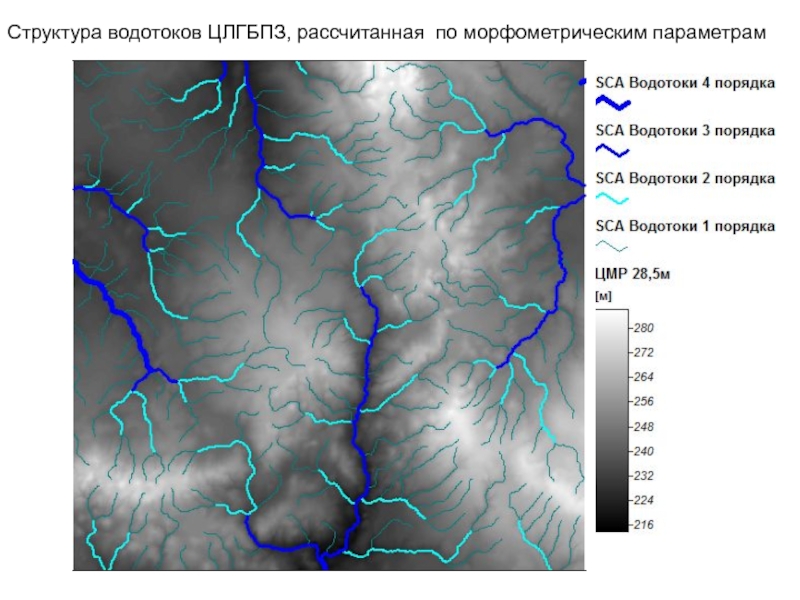
- 92. Структура водотоков ЦЛГБПЗ, рассчитанная по морфометрическим параметрам
- 93. Скачать презентанцию
Слайды и текст этой презентации
Слайд 1Географический факультет
Московского государственного университета им. М.В.Ломоносова
Landrus@geogr.msu.ru
Сысуев В.В.
доктор
географических наук, профессор
Слайд 2Современное ландшафтоведение –
комплексная физико-географическая наука
о пространственно-временной организации геосистем,
наука о структуре, функционировании и эволюции природных и природно-антропогенных территориальных
комплексов"В конечном счете, все физико-географические процессы
имеют в основе физические явления. Сведение географических закономерностей к геофизическим, а по мере возможности и к физическим законам представляется крайне желательным.
Только физический анализ убеждает, что явление понято»
[Д.Л. Арманд, 1975]
Слайд 3Направления исследования ландшафтоведения [К.Н.Дьяконов, 2004]
структурно-генетическое
структурно-функциональное
функционально-динамическое
геофизическое
геохимическое
социальный ландшафтогенез
палеоландшафтное
ландшафтная экология
ландшафтное планирование
геоэкологическое
эволюционное
физико-математическое (сквозное),
ПРЕДМЕТОМ КОТОРОГО ЯВЛЯЕТСЯ ТЕОРИЯ ГЕОСИСТЕМ,
состоящая из двух тесно взаимосвязанных частей: теории структуры и теории функционирования ландшафта
Слайд 4ЦЕЛЬ КУРСА
охарактеризовать физико-математический подход как теоретическую основу для
объединения основных направлений ландшафтоведения
ЗАДАЧИ:
продемонстрировать внутреннее единство теоретического описания структуры
геосистем и структурообразующих процессовпровести дедуктивное построение теории некоторых процессов в геосистемах от постулатов до уравнений математической физики, упрощение этих уравнений до практических моделей природных процессов
показать пути реализации моделей структуры и процессов функционирования геосистем вплоть до методик измерения и расчета физических параметров
применить теоретический подход в практических задачах ландшафтного планирования и гидрологического зонирования геосистем
Слайд 5наиболее важные методологические принципы (регулятивы) научной теории:
принципиальная проверяемость: должна быть
математически сформулированы, для возможности выведения количественных следствий, допускающих сравнение с
экспериментом.максимальная общность: должна объяснять новые стороны явлений, непосредственно не участвовавшие при ее создании
предсказательная сила: должна предвидеть совершенно новые до нее и без нее неизвестные явления, и чем лучше она это делает, тем большей предсказательной силой она обладает. Это возможно лишь тогда, когда теория содержит момент объективной истины
4) принципиальная простота: исходя из минимального числа основных
положений (основных, фундаментальных законов и принципов) теория должна вывести природные законы - теория должна обладать аппаратом выведения
Слайд 6развитие моделирования (на примере речного стока),
в связи с используемой
исходной априорной и экспериментальной (апостериорной) информацией [Кучмент, 1983]
Модели, при
построении которых априорная информация о структуре и параметрах гидрологической системы практически не используется: гидрологическая система рассматривается как "черный ящик"; Концептуальные модели стока, создаваемые при неполных и неопределенных физических представлениях о гидрологических процессах; однако ряд зависимостей и гипотетических связей уже используется при определении структуры модели и ее параметров;
Физико-математические модели формирования стока, основанные на достаточно полных физических представлениях и опирающиеся на измеряемые характеристики водосбора как основной территориальной системы; эти модели используют в основном априорную информацию.
физико-математический подход,
основанный на общенаучных понятиях и терминах, имеет Важное значение в плане включения частных процессов и систем в более общие геосистемы.
Слайд 7Основные предпосылки создания физико-математической теории геосистем
• Объективность существования ландшафтов
как отображения взаимодействия комплекса компонентов
• Эмпирическая классическая теория ландшафтоведения,
обобщения физической географии и синэкологии• Наличие и доступность достаточного и необходимого математического аппарата для адекватного описания процессов и структуры ландшафтов
• Опыт физико-математического моделирования отдельных природных процессов и элементов структуры ландшафтов.
• Активное развитие использования измерительных методов и ГИС-технологий в ландшафтных исследованиях
• Необходимость прогнозирования и планирования развития природной среды в прикладных целях
Слайд 8Геосистемы – открытые иерархически организованные
динамические системы, и каждый уровень
их иерархии
представляет собой динамичную целостность с особой
присущей им географической
организацией [Сочава, 1978]. Математическое определение системы-формализация понятия связи
Связь всегда означает взаимодействие объектов во времени. В результате
приходим к процессной точке зрения – система представляется
как взаимодействующие во времени процессы.
В каждый момент t система характеризуется некоторым состоянием –
элементом из множества ее состояний, которое однозначно определяет
значение выхода в этот момент t, и это одна из аксиом теории систем.
Внутреннее состояние системы S в момент времени t характеризуется
множеством значений ее параметров и их производных.
Если в понятия системы использование процессов входа и выхода
было вызвано физическими представлениями о функционировании системы,
то понятие состояния имеет отношение к закону формирования выхода.
Т.е., существует еще одна характеристика – закон, которому подчиняется
поведение системы в пространстве состояний
Слайд 9ЭТАПЫ РАЗРАБОТКИ ТЕОРИИ ГЕОСИСТЕМ
1.Систематизация структурообразующих геосистемных процессов
2.Формализация пространственной структуры геосистем
3.Создание,
верификация, идентификация, параметризация моделей
Радиальные процессы формирования элементарных геосистем
Латеральное сопряжение
геосистем элементарного водосбора Формирование структуры геосистем высоких иерархических порядков
Элементарные геосистемы:
земная поверхность в поле гравитации (конвергенция-дивергенция и ускорение-замедление потоков) и
в поле инсоляции (освещенность, доза солнечной радиации и др.)
Параметры структуры водосборов:
поверхностных - линии тока, водоразделы, тальвеги, порядок водосбора и др.; подземных - почвенные и литологические горизонты и линеаменты, и др.
Радиальные процессы переноса в элементарных геосистемах: биогенные (продуктивность, сукцессии, малый биокруговорот );
атмогенные (радиационный, конвективно-диффузионный и др)
гидроциркуляционные (транспирация, трансформация осадков растительностью, влагомассоперенос в почвах, и др.)
Процессы латерального переноса на водосборах, барьеры и др.
Слайд 11ВЫБОР ПАРАМЕТРОВ ЭТО ВВЕДЕНИЕ АКСИОМАТИКИ
Т. о. природные объекты и процессы
могут дифференцироваться по
1) определяющим потокам Ji ,
2) движущим
силам Xk - градиентам потенциалов силовых полей U, 3) по обобщенной проводимости Lik , либо по всем одновременно.
Для описания потоков, сил и проводимостей необходимо использовать применяющиеся в географии численные параметры:
цифровых моделей рельефа (ЦМР)
- цифровых данных дистанционного зондирования (ДДЗ)
- измеряемые параметры в ландшафтных, лесотаксационных, гидрологических, гидрогеологических, геофизических и др. исследованиях
Систематизация структурообразующих процессов.
Обобщенный поток Ji в термодинамике необратимых процессов => => билинейное уравнение Онзагера
Слайд 12Основные геосистемные аксиомы и постулаты
Геометрия пространства геосистем низких рангов с
высокой степенью точности является евклидовой.
Принцип инерции Галилея выполняется во
всех геосистемах. Инерциальность геосистем обеспечивает инвариантность физических законов относительного перехода из одной системы в другую. Все геосистемы состоят из макроскопических тел, состоящих из очень большого количества атомов (молекул), имеют размеры более 10-8 - 10-7 м, и подчиняются классическим законам нерелятивистской механики.
Модельным представлением описания структуры объектов и тел является материальная точка (частица) и абсолютно твердое тело.
Состояние любой физической системы определяется набором независимых друг от друга величин и функций состояния.
Все фундаментальные силы в геосистемах имеют гравитационную и электромагнитную природу.
Потенциальное поле и градиент потенциала – движущая сила потоков и в целом развития систем.
Материальные точки геосистем находятся под воздействием одновременно большого числа независимых физических полей, их динамика реализуется в многомерном поле сил. Это в явном виде описывается уравнением неравновесной термодинамики Онзагера.
Математические модели и, в частности, уравнения математической физики в силу своей общности – основа развития теоретической базы ландшафтоведения, и развития натурных наблюдений и экспериментов.
Источником гипотез являются эмпирические обобщения физической географии
Слайд 14(х,t) - линейная плотность среды, ma,b – масса на участке
a-b, V- объем
Параметры и функции состояния материальных систем
тi - масса
является мерой инерции частицы, т0 – масса эталона. В последнем выражении мы задаем важную процедуру измерения параметров состояния
х, у, z – координаты, vx , vy , vz - компоненты скорости материальной точки (тела) в заданный момент времени t
Опытным путем установлено, что для изолированных систем, состоящих из N материальных точек, скорости которых v1,…,vN , частицы характеризуются некоторыми определенными константами m1,...,mN , такими, что
q(x,t) - потоком массы, локальный параметр среды
Слайд 15Силовые поля и взаимодействия
Производная импульса частицы во времени есть сила
F,
действующей на частицу со стороны ее окружения
Фундаментальные взаимодействия: гравитационные,
электромагнитные, слабые и сильные (ядерные)Принцип гравитационного дальнодействия
G – гравитационная постоянная (6,672∙10-11 м3/кг∙с),
экспериментально гравитационные массы совпадают с инерционными массами с точностью до 10-11 – их тождество постулат ОТО
Для электромагнитных взаимодействий Фарадей ввел представление о поле, которое оказывает силовое воздействие на заряд. Изменения энергии (импульса) заряженной частицы передаются окружающему электромагнитному полю, которое само по себе обладает энергией и импульсом, и может существовать .самостоятельно (например, световые волны, радиоволны и др.)
Слайд 16Сплошная среда
Исследование материальных тел - построение макроскопической теории, основанной
на общих закономерностях и гипотезах, полученных опытным путем.
Первая гипотеза -
переход от системы точек к сплошной среде. Все тела состоят из отдельных частиц, которых очень много в любом существенном для геосистем объеме. Поэтому каждое тело рассматривается как среда, сплошным образом заполняющая предоставленную часть пространства. Такая идеализация позволяет использовать аппарат дифференциального и интегрального исчисления.Вторая гипотеза определяет пространство, в котором рассматривается материальное тело, как совокупность точек, задаваемых числами – координатами точек. Все объекты будем изучать в евклидовом пространстве, в котором вводится единая для всех точек декартова прямоугольная система координат (x1, x2, x3, или x, y, z), и между любыми двумя точками А и В определено расстояние – евклидова метрика – по формуле:
Третья гипотеза - используется абсолютное время. Т.е. мы не будем учитывать эффекты теории относительности. Будем изучать поведение сплошной среды – континуума в евклидовом пространстве с использованием абсолютного времени и будем базироваться на законах термодинамики необратимых процессов и механики сплошной среды.
Слайд 17Потенциальное силовое поле и градиент потенциала
Работа равна произведению силы
на расстояние, пройденное телом под воздействием этой силы. Элементарная работа
dA сил, действующих на материальную точку системы: (1)Поле сил называется потенциальным, если существует такая скалярная функция координат точки U (x, у, z), что частные производные от этой функции по x, у, z равны проекциям Fx, Fy, Fz вектора силы на эти оси:
(2)
Подставляя (2) в (1) получим:
(3)
Элементарная работа равна полному дифференциалу функции dU, называемой потенциальной энергией, которая зависит только от положения частицы и не зависит от пути, пройденного частицей. Вектор с компонентами (дU/дх, дU/ду, U/z) называется градиентом функции U:
(4)
Слайд 18dsABCD=dzdy
dsABCD = dydz
divA - скаляр дивергенция, или расходимость
вектора А
▼Поток величины, дивергенция вектора
Рассмотрим поток J вектора A в трехмерном пространстве
Приращение потока по оси х:
(5)
Слайд 19ВРАЩЕНИЕ ФОРМА ЗЕМЛИ И СИЛА ТЯГОТЕНИЯ
Уменьшение силы
тяжести вследствие вращения Земли.
fц = ω2Rcosφ
g =
F – fц ;рад/сек
f цэкв = 3,39158 гал (см/с2 ), f цпол =0
Геодинамическая постоянная q – отношение центробежной силы к силе тяготения:
= 978,0318 (1+0,0053024 sin2 – 0,0000059 sin2 2)
нормальная удельная сила тяжести в зависимости от широты:
(6)
Слайд 20Гравитационный потенциал частицы в поле гравитации ,
обращающийся в нуль при бесконечном удалении частицы массы m от
силового центра массой M, равен и соответственно (4) сила притяженияВ геофизике декартова система координат задается традиционно: ось 0z совпадает с осью вращения планеты, две другие оси лежат в экваториальной плоскости, т.е. компоненты вектор силы (2) равны Fx = – Gmx/r3 , Fy = – Gmy/r3 , Fz = – Gmz/r3
Гравитационный потенциал Земли. По принципу суперпозиции гравитационный потенциал n точек равен сумме гравитационных потенциалов всех точек, т.е. для тела V можно записать
(7)
Вектор напряженности гравитационного поля в точке с радиус-вектором r равен силе, которая действует на материальную точку с массой, равной единице
Приближенное решение (3) получено для Земли с помощью разложения в ряд полиномами Лежандра:.
(8)
(9)
Слайд 23 Описание пространственной структуры геосистем 1. ТИПОЛОГИЧЕСКИЙ ПОДХОД ВЫДЕЛЕНИЯ ПТК :
Элементарный ПТК - приурочен к одному элементу мезорельефа; это территория
однородная по трем своим характеристикам: литологическому (петрографическому) составу пород, углам наклона рельефа и экспозиции склона. В этом случае суммарная солнечная радиация и атмосферные осадки, поступающие на поверхность, одинаковы. Поэтому формируются один микроклимат и один водный режим, один биогеоценоз, одна почвенная разность и однообразный комплекс почвенной мезофауны [Дьяконов, 2004].Следовательно:
потенциальная дифференциация ПТК может быть определена на множестве элементов поверхности рельефа отображением морфометрических параметров описания градиентов полей инсоляции и гравитации.
Уравнения теории поля и дифференциальной геометрии являются как минимум достаточным условием для геофизического описания потенциальной дифференциации природных территориальных комплексов.
Слайд 24Классы морфометрических величин и понятий [Шарый, 1995].
2. ВЫБОР ПАРАМЕТРОВ
ПРОСТРАНСТВЕННОЙ СТРУКТУРЫ ГЕОСИСТЕМ
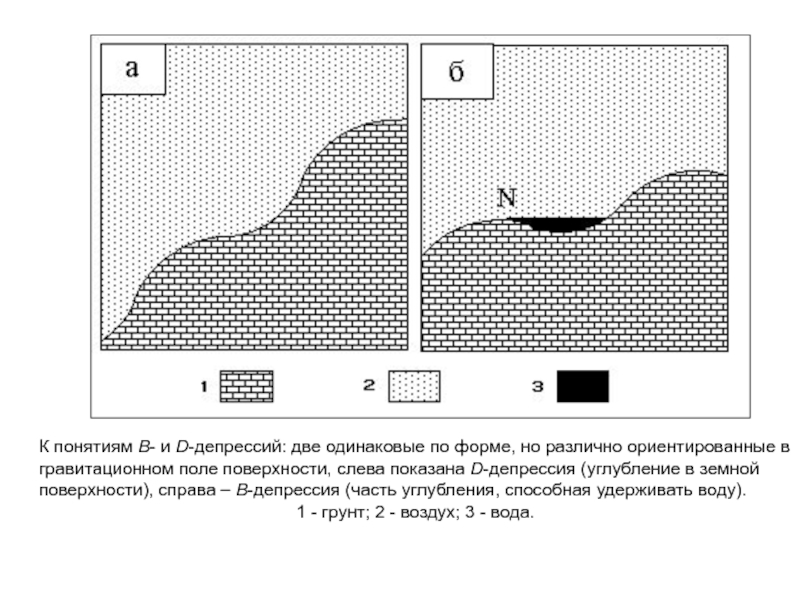
Слайд 25К понятиям В- и D-депрессий: две одинаковые по форме, но
различно ориентированные в гравитационном поле поверхности, слева показана D-депрессия (углубление
в земной поверхности), справа – В-депрессия (часть углубления, способная удерживать воду).1 - грунт; 2 - воздух; 3 - вода.
Слайд 26Формулы расчета локальных морфометрических величин [Shary, 1995]. ( p=z/x; q=z/y; r=2z/x2;
s=2z/xy; t=2z/y2, z=z(x,y)).
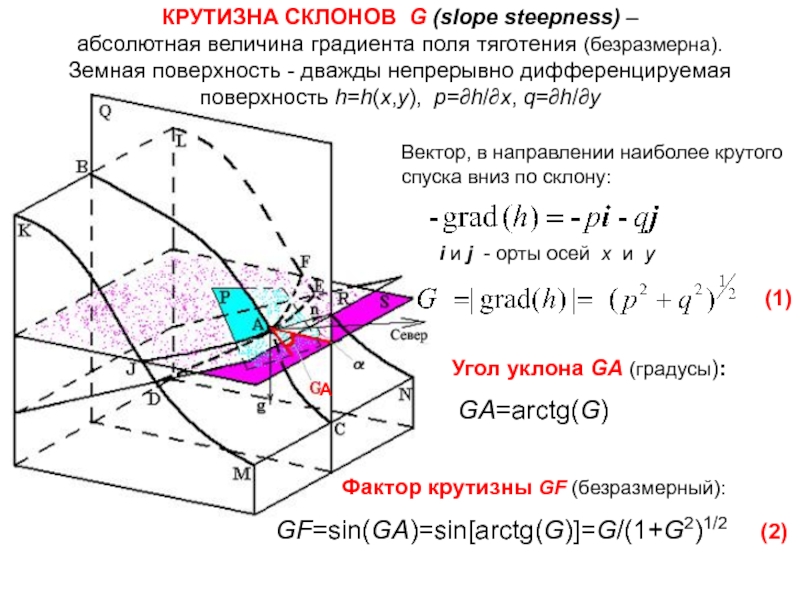
Слайд 27КРУТИЗНА СКЛОНОВ G (slope steepness) –
абсолютная величина градиента поля
тяготения (безразмерна).
Земная поверхность - дважды непрерывно дифференцируемая поверхность hh(x,y), ph/x,
qh/y Вектор, в направлении наиболее крутого спуска вниз по склону:
i и j - орты осей x и y
Угол уклона GA (градусы):
GAarctg(G)
Фактор крутизны GF (безразмерный):
GFsin(GA)sin[arctg(G)]G/(1+G2)1/2 (2)
(1)
А
Слайд 28В точках поверхности h(x,y) определим вектор единичной длины -grad(h)/G; обозначая
через u направленный вдоль этого вектора элемент длины на карте
(т.е. на плоскости z0), находимdr/du -grad(h)/G -(pi+qj)/(p2+q2)1/2 , (4)
где r(x,y) - вектор определяющий положение точки на карте. Линия, касательная к которой есть dr/du, называется линией тока; вдоль этих линий течет вода.
Дифференцируя уравнение горизонтали h(x,y)const по длине горизонтали v, находим
pdx/dv+qdy/dv0.
Из курса математического анализа известно, что для плоской кривой
(dx/dv)2+(dy/dv)21;
из последних двух равенств следует
dr/dv (-qi+pj)/(p2+q2)1/2 (5)
По формулам (4) и (5) проверяется, что скалярное произведение (dr/du,dr/dv) равно нулю. Этим доказано, что горизонтали и линии тока взаимно перпендикулярны; на карте они образуют криволинейную ортогональную сетку.
( p=z/x; q=z/y; r=2z/x2; s=2z/xy; t=2z/y2, z=z(x,y)).
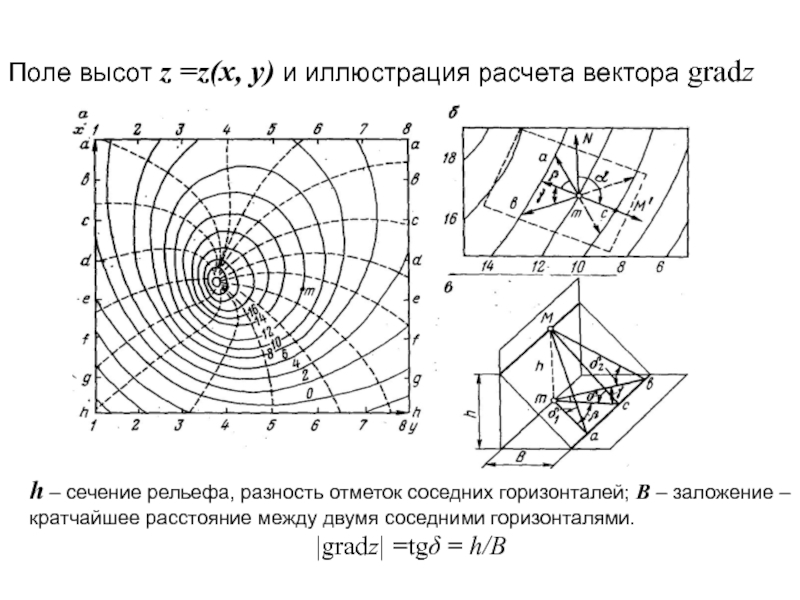
Слайд 29Поле высот z =z(х, у) и иллюстрация расчета вектора gradz
h – сечение рельефа, разность отметок соседних горизонталей; В –
заложение – кратчайшее расстояние между двумя соседними горизонталями.|gradz| =tg = h/B
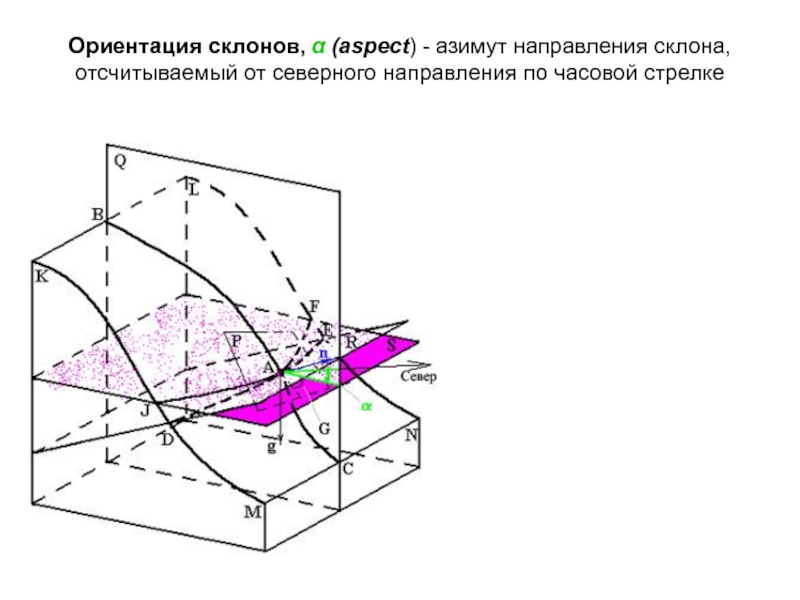
Слайд 30Ориентация склонов, α (aspect) - азимут направления склона, отсчитываемый от
северного направления по часовой стрелке
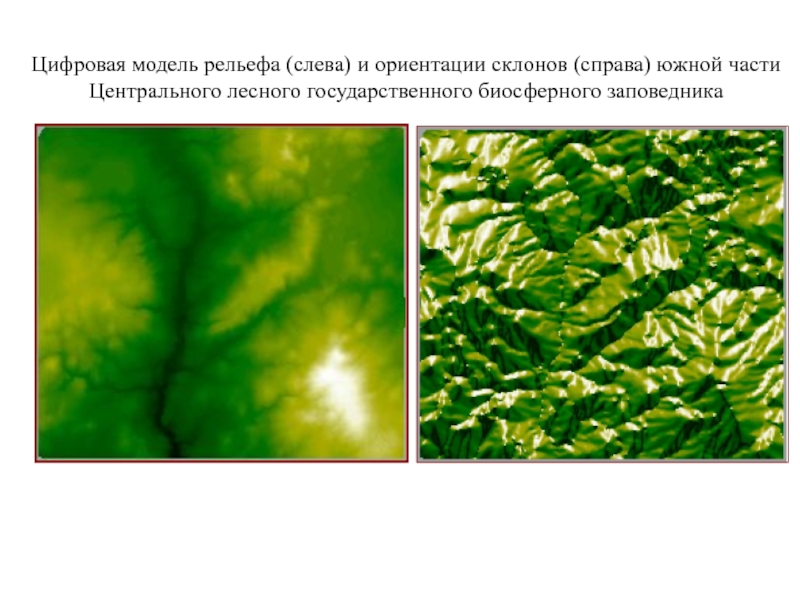
Слайд 31Цифровая модель рельефа (слева) и ориентации склонов (справа) южной части
Центрального лесного государственного биосферного заповедника
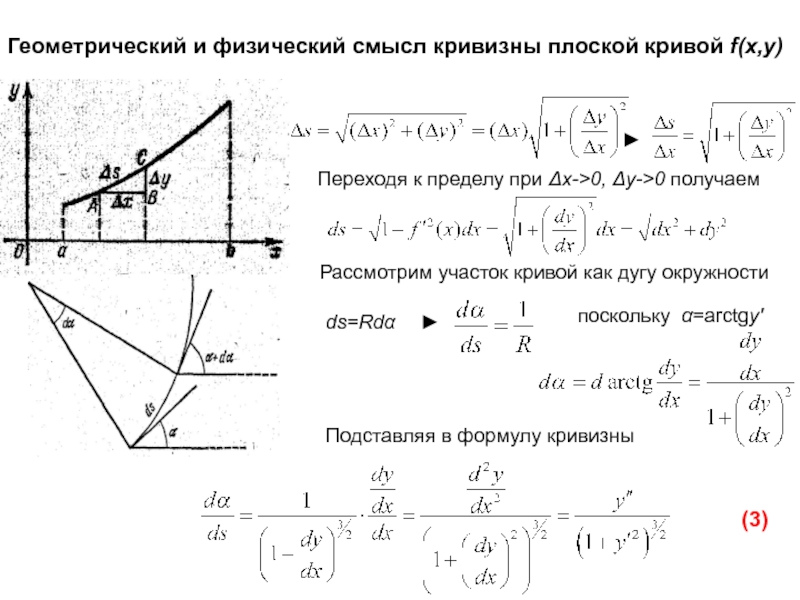
Слайд 32Переходя к пределу при Δx->0, Δy->0 получаем
ds=Rd
►
Рассмотрим участок кривой
как дугу окружности
поскольку =arctgy'
►
Подставляя в формулу кривизны
Геометрический и
физический смысл кривизны плоской кривой f(x,y)(3)
Слайд 34Геометрический и физический смысл системы кривизн на основе понятие нормального
сечения поверхности
Слайд 35К ОПИСАНИЮ ДВУХ ОСНОВНЫХ МЕХАНИЗМОВ АККУМУЛЯЦИИ [ШАРЫЙ,1991]. Слева – первый
механизм аккумуляции, сближение потоков; второй механизм аккумуляции за счет относительного
замедления потоков. 1 –зоны дивергенции, 2 –зоны конвергенции, 3 –горизонтали, 4 – грунт, 5 –воздух.Слайд 36Теорема: О первом механизме аккумуляции (Shary,1995)
Для неособых точек дважды
непрерывно дифференци-руемой поверхности дивергенция единичного вектора
dr/du линий тока равна плановой
кривизне kp.Доказательство.
div(dr/du)(dx/du)/x+(dy/du)/y
и согласно (4),
dx/du -p/(p2+q2)1/2, dy/du -q/(p2+q2)1/2;
дифференцируя эти выражения по x и y, соответственно, находим
div(dr/du) -(q2r-2pqs+p2t)/(p2+q2)3/2.
Но правая часть этого равенства есть kp, согласно (7).
Т.о., div(dr/du)kp.
Теорема доказана
Первый механизм аккумуляции - сближение линий тока в участках местности, где kp0 (или kh0), и расхождение их в тех участках местности, где kp0 (или kh0).
( p=z/x; q=z/y; r=2z/x2; s=2z/xy; t=2z/y2, z=z(x,y)).
Слайд 38Теорема: О втором механизме аккумуляции. Для неособых точек дважды непрерывно
дифференцируемой поверхности производная фактора крутизны GF по длине линии тока
u равна вертикальной кривизне kv.Доказательство. По формуле (2) GFG/(1+G2)1/2, откуда производная
dGF/du [dG/du(1+G2)1/2-G2(dG/du)(1+G2)-1/2]/(1+G2)(dG/du)/(1+G2)3/2,
т.е. dGF/dudG/du(1+G2)-3/2.
Поскольку G(p2+q2)1/2,
dG/du(pdp/du+qdq/du)/(p2+q2)1/2 {p[(dp/dx)(dx/du)+(dp/dy)(dy/du)]+q[(dq/dx)(dx/du)+(dq/dy)(dy/du)]}/(p2+q2)1/2
или dG/du{p[r(dx/du)+s(dy/du)]+q[s(dx/du)+t(dy/du)]}/(p2+q2)1/2 [(pr+qs)dx/du+(ps+qt)dy/du]/(p2+q2)1/2.
Подставляя сюда выражения для dx/du и dy/du из (2.2), находим для производной dG/du :
dG/du -[(pr+qs)p+(ps+qt)q] /(p2+q2) -(p2r+2pqs+p2t)/(p2+q2).
Теперь из dGF/du dG/du(1+G2)-3/2 получаем
dGF/du -(p2r+2pqs+p2t)/[(p2+q2)(1+p2+q2)3/2],
и сравнивая это выражение с (6), находим dGF/dukv. Теорема доказана.
Второй механизм аккумуляции - фактор крутизны (а с ним и крутизна) уменьшается при смещении вдоль линии тока вниз по склону на вогнутых по профилю участках (где kv0), и увеличивается – на выпуклых (где kv0).
Слайд 40Горизонтальная кривизна Kh (слева) и вертикальная кривизна Kv (справа). Светлый
цвет – области выноса; темный – области аккумуляции
Слайд 41Карта зон относительной аккумуляции и сноса (элементарных геосистем) леспаркхоза «Горки»
в южной части Подмосковья.
Слайд 42Вероятные места обнаружения зоны аккумуляции показаны темным (чем темнее, тем
выше вероятность). Точками показан трансект, на котором получены эмпирические данные
[Шарый, 2016]. Подходящая функция связи для биномиальное распределения известна как логит, logit(W)=ln[W/(1-W)], где W есть вероятность наличия; соответствующая модель логит-регресси уравнениеln[W/(1-W)]=a∙X+b∙Y+c.
Предсказанные зоны аккумуляции для участка «Данки» (Приокско-террасный Заповедник).
Уравнение множественной логит-регрессии
ZСР=158.8 м, khSD=0.0004922 1/м, критическое значение t-статистики t0.05,28=2.048.
ln[p/(1-p)]А33= –0.02342∙Y–14.90+0.003600 (Z-ZСР)3+9.82+7.340∙sin(A0) +5.78+ 0.6787∙khП+2.95+142562,
R2 = 0.897 (Degr= 5.3%), P<10–6.
Слайд 43Удельная площадь водосбора (слева) и дисперсивная площадь (справа). Темные пятна
на правой карте – моренные холмы и гряды
Слайд 44 В точке А вылито 220 литров сырой нефти. Линии –
горизонтали, точки – места отбора проб, контур – область поверхностного
загрязнения, оттенками показана область распространения. Хорошо видна реальность разветвления нефти при ее течении по земле. На каждом холмике нефть разветвлялась, сливаясь следом за ним.Эксперимент по разливу нефти в ландшафте.
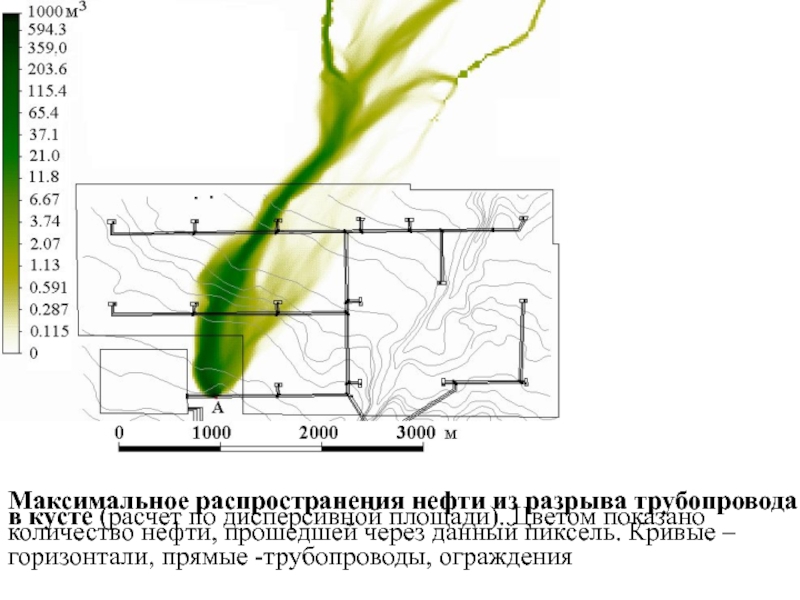
Слайд 45Максимальное распространения нефти из разрыва трубопровода в кусте (расчет по
дисперсивной площади). Цветом показано количество нефти, прошедшей через данный пиксель.
Кривые – горизонтали, прямые -трубопроводы, огражденияСлайд 48 Морфометрическая дневная доза прямой солнечной радиации 22 июня и
22 декабря на северо-восточном побережье Черного моря (Зайцев, 2001)
Слайд 493. Общий алгоритм определения однородной территории по параметрам
создание метрического
пространства параметров - выбор, обоснование методов получения и расчета содержательных
величин, описывающих структурообразующие процессысоздание пространства географических координат - выбор масштаба, создание цифровой модели рельефа с заданным разрешением и т.д.
отображение пространства параметров на пространство координат - создание матрицы, где столбцы - параметры, а строки - координаты элемента, к которому относятся параметры.
задание метрики пространства и создание матрицы дистанций
задание меры (признака) однородности.
определение однородной территории по пространству параметров.
Слайд 50Выбор и группировка морфометрических величин (МВ), описывающих градиенты полей гравитации
и инсоляции
МВ описывающие факторы перераспределения солнечной (и тепловой) энергии:
экспозиция и освещенность склонов; уклон; высота; доза прямой солнечной радиации (дневная, годовая).МВ описывающие распределение и аккумуляцию воды под действием силы тяжести: уклон; удельная площадь сбора и удельная дисперсивная площадь; глубина В-депрессий и высота В-холмов.
МВ описывающие механизмы перераспределения вещества под действием гравитации: уклон; высота; горизонтальная и вертикальная кривизна.
Наименьшими материальными точками, из которых состоят пространственно-территориальные комплексы, выступают элементы поверхности рельефа (практически пиксели цифровой модели местности), имеющие географические координаты, а их состояние описывается параметрами градиентов геофизических полей.
Слайд 51Морфометрические параметры рельефа Национального парка «Валдайский»: ориентация склонов - (слева),
относительная величина годового радиационного баланса – справа,
вертикальная кривизна –
слева, удельная площадь водосбора – справа Слайд 52Классификация поверхности рельефа ЦЛГПБЗ по параметрам перераспределения прямой солнечной радиации
и тепла
Слайд 53Дифференциация поверхности рельефа по морфометрическим параметрам распределения солнечной радиации и
тепла
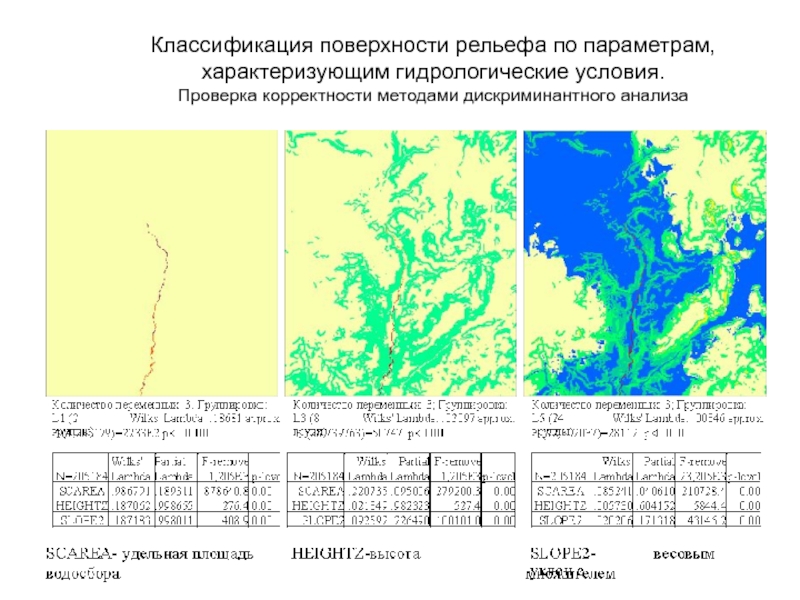
Слайд 54Классификация поверхности рельефа по параметрам, характеризующим гидрологические условия. Проверка корректности
методами дискриминантного анализа
Слайд 55Дифференциация рельефа по морфометрическим параметрам распределения гидрологического стока и заболачивания
Слайд 56Дифференциация рельефа по морфометрическим параметрам ландшафтно-геохимических механизмов переноса
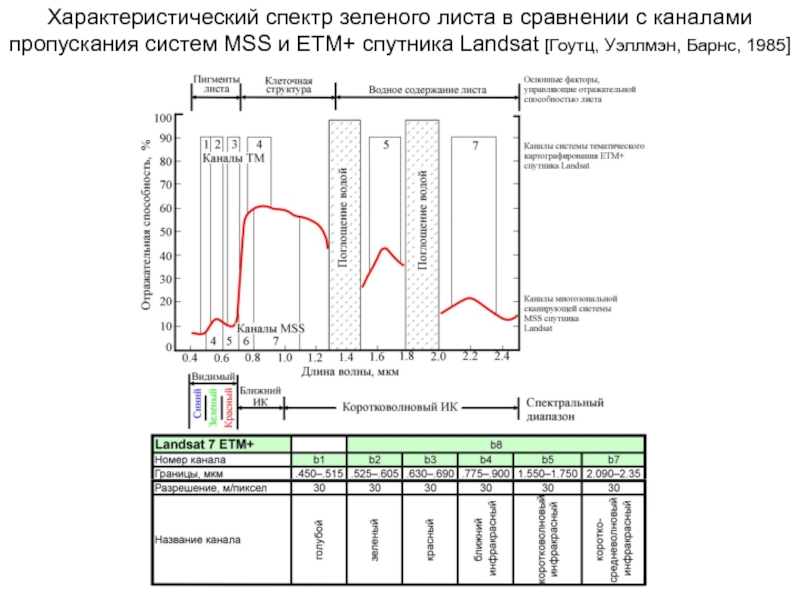
Слайд 58Характеристический спектр зеленого листа в сравнении с каналами
пропускания систем
MSS и ETM+ спутника Landsat [Гоутц, Уэллмэн, Барнс, 1985]
Слайд 59Физическая информация спектральных каналов съемки LANDSAT.
1 канал (голубой):
Наиболее чувствителен к
атмосферным газам, изображение канала пестрее остальных;
Волны диапазона имеют наибольшую водопроницаемость,
данный канал оптимален для изучения подводной растительности, мутности воды, водных осадков и загрязнения воды;Полезен для выявления дымовых факелов, т.к. короткие волны легче рассеиваются маленькими частицами;
Хорошо отличает облака от снега и горных пород, а также голые почвы от участков с растительностью.
2 канал (зеленый):
Чувствителен к мутности воды, осадочным шлейфам и факелам выбросов;
Охватывает пик отражательной способности поверхностей листьев, полезен для различения обширных классов растительности;
Полезен для изучении подводной растительности, факелов выбросов, мутности и осадков.
3 канал (красный):
Чувствителен в зоне сильного поглощения хлорофилла, и растительности;
Чувствителен в зоне высокой отражательной способности большинства почв;
используется для картографирования снежного покрова.
Слайд 604 канал (ближний инфракрасный):
Связан со свойствами растительности.
Максимально чувствителен к
различиям породного состава.
5 канал (коротковолновый инфракрасный):
Чувствителен к содержанию воды в
тканях листьев (отражательная способность уменьшается при возрастании содержания воды); полезен для определения
энергии растений и отделения суккулентов от древесной растительности;
Чувствителен к наличию трехвалентного железа в горных породах (отражательная способность возрастает при увеличении количества Fe+3);
Отличает лед и снег (светлый тон) от облаков (темный тон).
6 канал (длинноволновый инфракрасный или тепловой):
Измерение температуры излучающей поверхности от –100 до +150С (дневное и ночное);
Применение съемки: анализ влажности почв, типов горных пород,
выявление теплового загрязнения воды, бытового скопления тепла, источников
городского производства тепла, эффективное военное наведение, инвентаризация живой природы, выявление геотермальных зон.
7 канал (средний или коротковолновый инфракрасный):
Совпадает с полосой поглощения излучения гидроминералами (глинистые сланцы, некоторые оксиды и сульфаты); полезен для литологической съемки;
Чувствителен к варьированию влаги в растительности и почвах.
Слайд 61 Нормализованный разностный вегетационный индекс (Normalized Difference Vegetation Index ).
NDVI вычисляется как отношение значений спектральной яркости в красной и
ближней инфракрасной зонах спектра: NDVI=(ближний инфракрасный–красный)/(ближний инфракрасный + красный).Для каналов Landsat 7 формула следующего вида:
NDVI=(канал 4 – канал 3)/(канал 4 + канал 3).
2. Нормализованный разностный снеговой индекс (Normalized Difference Snow Index ). NDSI чувствителен к мощности снега, льда Для каналов Landsat 7 формула следующего вида:
NDSI=(канал 1 – канал 4)/(канал 4 + канал 1).
3. Нормализованный разностный влажностный индекс (Normalized Difference Water Index ). NDWI
и др.
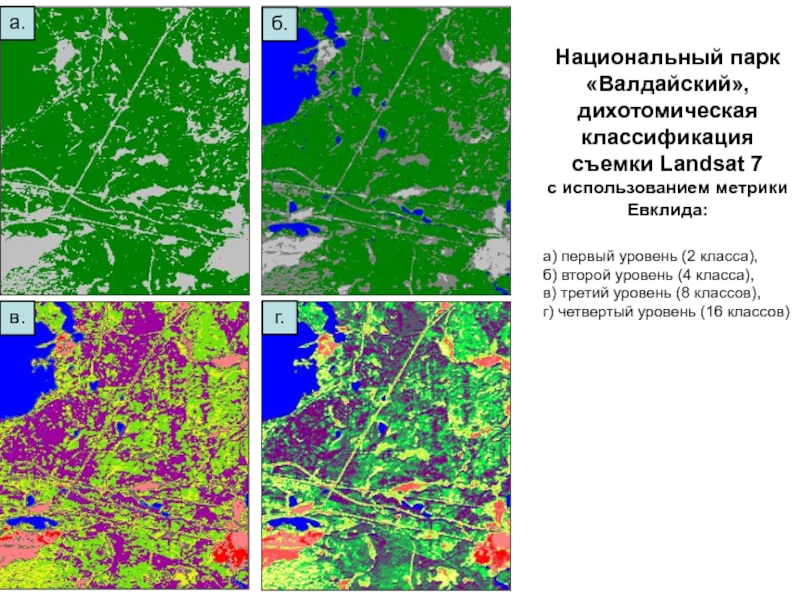
Слайд 62Национальный парк «Валдайский», дихотомическая классификация съемки Landsat 7
с использованием
метрики Евклида:
а) первый уровень (2 класса),
б) второй уровень (4
класса),в) третий уровень (8 классов),
г) четвертый уровень (16 классов)
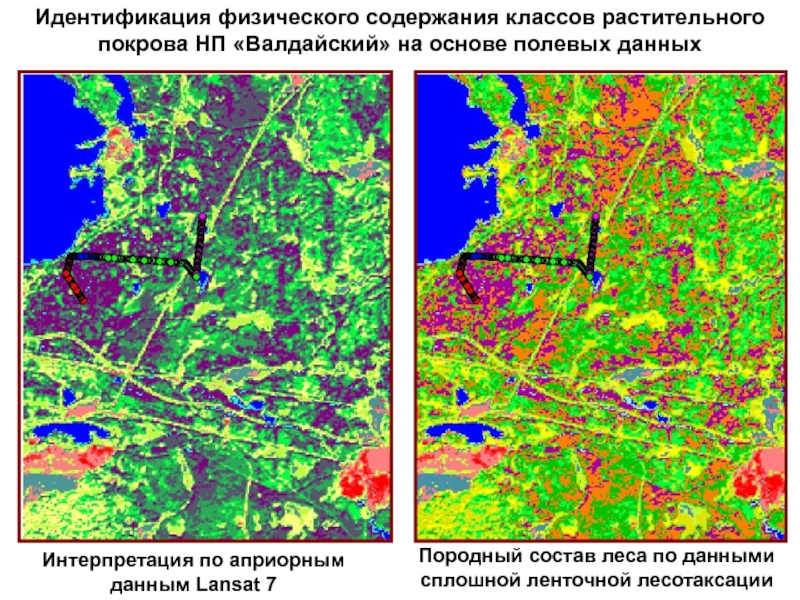
Слайд 63Идентификация физического содержания классов растительного покрова НП «Валдайский» на основе
полевых данных
Породный состав леса по данными сплошной ленточной лесотаксации
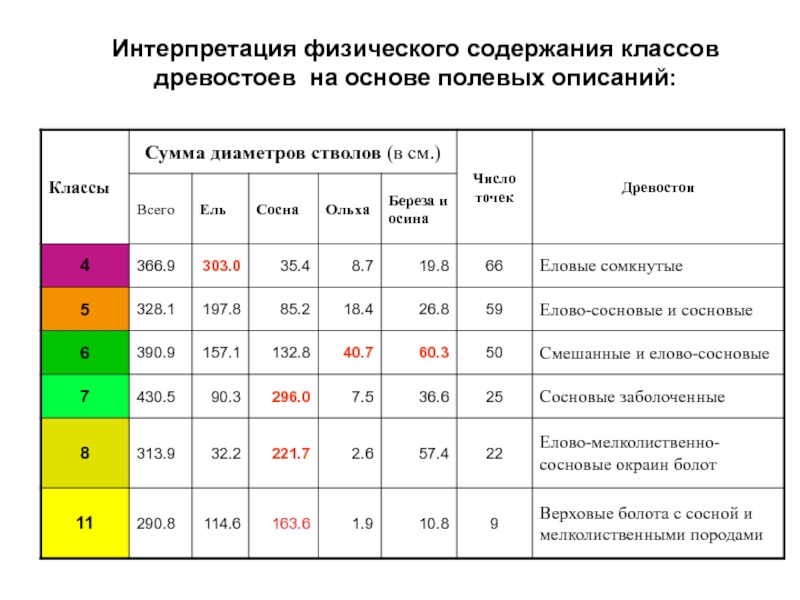
Интерпретация
по априорным данным Lansat 7Слайд 64Значение натурных наблюдений в разработке теории геосистем
1. Измерения в натуре
- важнейший источник физических параметров теоретических моделей геосистем.
2. Модель задает
набор параметров, точность и дискретность их измерений3. Картирование природных территориальных комплексов и их компонентов на ключевых территориях ( трансектах) – важнейший метод верификации моделей и, следовательно, построения теории геосистем.
4. Обеспечение цикла развития «теория→эксперимент →теория →….»
Методы полевых исследований
Традиционные ландшафтные и покомпонентные (геоботанические, лесотаксационные, почвенные и др.) полевые методы исследования и картографирования.
Автоматизированные комплексы стационарной и полустационарной регистрации физических и химических параметров приземных слоев атмосферы, природных вод и почв и растений.
Методы прикладной геофизики (сейсмические, гравитационные, электромагнитные, георадарные, и др.), мобильные и производительные автоматизированные методы мониторинга почвенных, литологических и гидрогеологических условий.
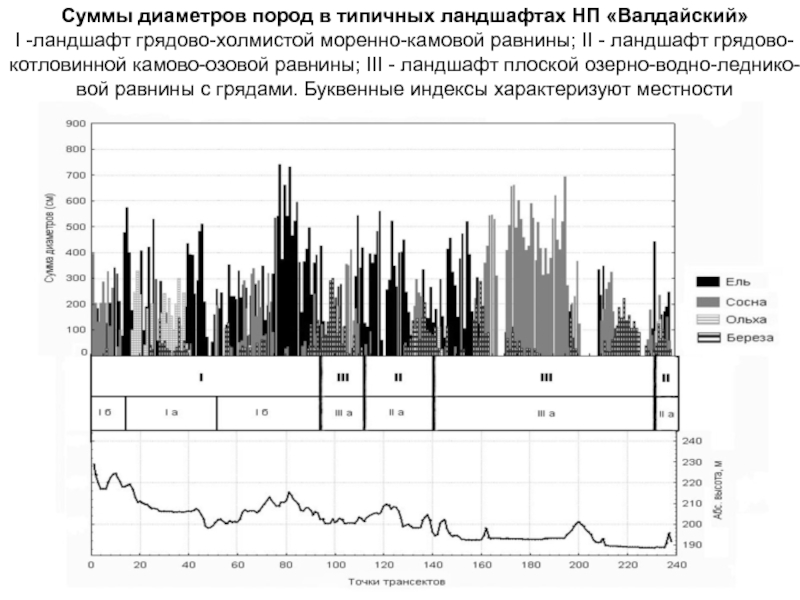
Слайд 65Суммы диаметров пород в типичных ландшафтах НП «Валдайский»
I -ландшафт
грядово-холмистой моренно-камовой равнины; II - ландшафт грядово-
котловинной камово-озовой равнины; III
- ландшафт плоской озерно-водно-леднико-вой равнины с грядами. Буквенные индексы характеризуют местности
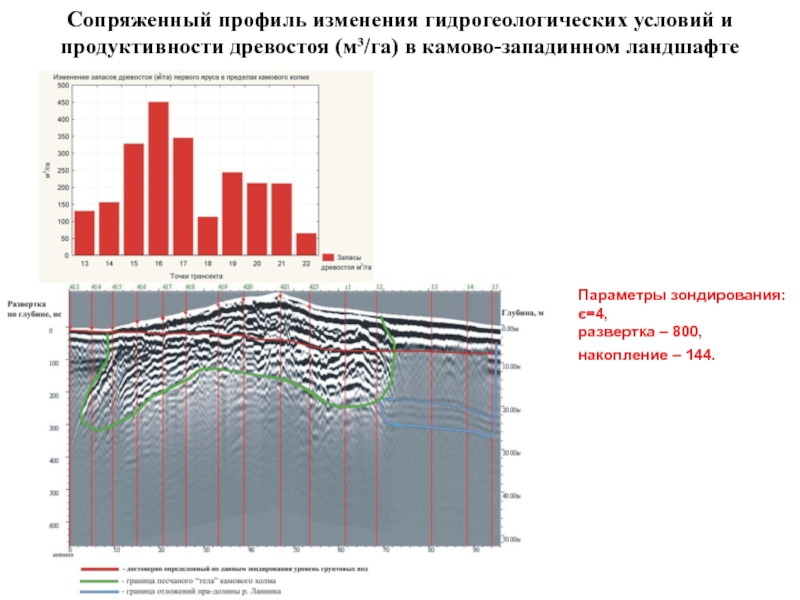
Слайд 67Сопряженный профиль изменения гидрогеологических условий и продуктивности древостоя (м³/га) в
камово-западинном ландшафте
Параметры зондирования:
є=4,
развертка – 800,
накопление – 144.
Слайд 68Пространственная привязка линзы водонасыщенных флювиогляциальных песков, обнаруженной георадарной съемкой под
покровными суглинками (площадной разрез на глубине 2,5 м)
Водонасыщенные
флювиогляциальные пескиМоренные суглинки и их делювий
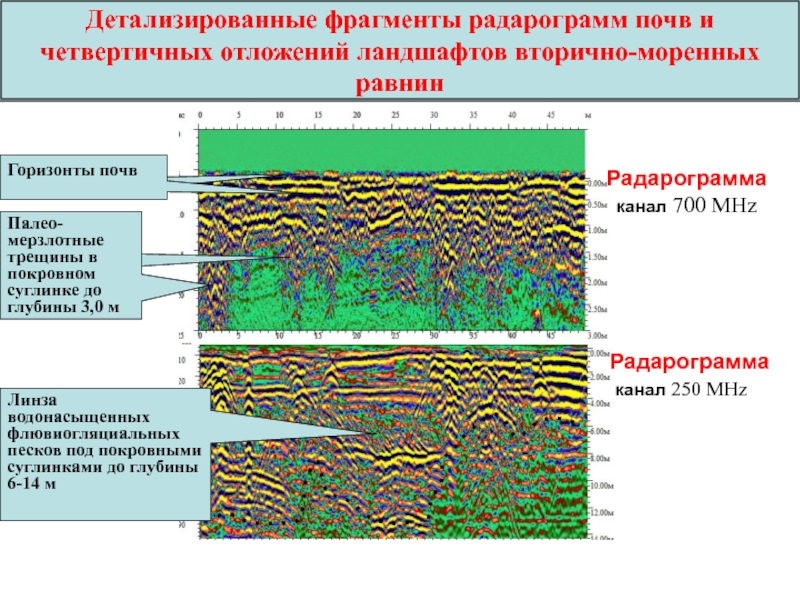
Слайд 69Детализированные фрагменты радарограмм почв и четвертичных отложений ландшафтов вторично-моренных равнин
Палео-мерзлотные трещины в покровном суглинке до глубины 3,0 м
Линза водонасыщенных
флювиогляциальных песков под покровными суглинками до глубины 6-14 мРадарограмма канал 700 MHz
Soil horizons
Радарограмма
канал 250 MHz
Горизонты почв
Слайд 70моренные гряды и камовые холмы с
суглинистыми дерново-подзолистыми
почвами под
разнотравно-кисличными
ельниками
вершины камовых холмов и дюнных
гряд с песчаными
дерново-подзолами под сосняками зеленомошными,
беломошными и разнотравными
плоские и выпуклые верховые болота
с мощными торфами с редкостойными
сосняками сфагновыми
речные и озерные террасы с дерново-
и торфяно-глеевыми почвами под
ельниками и смешанными лесами
подножья холмов и плоские вогнутые
ложбины с дерново-глеевыми и дерново
подзолистыми контактно отбеленными
почвами под смешанными лесами
дюнные гряды и песчаные холмы с
дерново-подзолистыми почвами под
сосняками
речные поймы с дерново-глеевыми
почвами под заливными лугами
крутые склоны холмов и гряд разного
генезиса с дерновыми почвами под
хвойными лесами
антропогенно измененные и
антропогенные ландшафты (дороги,
просеки ЛЭП, карьеры, сельсхозугодья,
лесопитомники и селитебные)
Карта структуры ПТК на основе классификации рельефа по параметрам
градиентов геофизических полей и космического снимка Landsat-7
Слайд 71Ландшафтная карта исследованной части национального парка «Валдайский».
Слева карта (урочища,
местности и ландшафты), составленная классическим методом по
полевым данным и
материалам ДДЗ [Сысуев, Солнцев, 2006].Справа карта, полученная методом К-средних для 8 кластеров по нормированным параметрам
(6 каналов+NDVI, ETM/Landsat-7 и 4 параметров ЦМР – Z1, SCALg, RadB, Z2), с наложенными
границами местностей и ландшафтов взятых с ландшафтной карты (слева)
Слайд 724. ФУНКЦИОНАЛЬНО-ДИНАМИЧЕСКАЯ КЛАССИФИКАЦИЯ ГЕОСИСТЕМ
Функциональный подход - выявление механизмов современных взаимодействий,
объединяющих природные объекты в функционирующие как единое целое геосистемы.
Потоки
вещества и энергии высокой интенсивности обладают способностью формировать специфический рельеф (флювиальный, гляциальный, эоловый и т.д.), а также прямо или косвенно обусловливать распределение и численность растений и животных, особенности почвенного покрова, воздействовать на другие потоки. Таким образом, они образуют сферу влияния, которая и есть геосистема . В бореальных условиях главным структурообразующим потоком является водный сток.Следовательно:
геосистемы различных порядков могут быть выделены в соответствии со схемой Стралера-Философова на множестве элементов рельефа по значениям морфометрических величин, описывающих распределения воды в поле гравитации:
водоразделы любого порядка одновременно соответствуют локальным: максимумам высоты h, минимумам величины удельной площади водосбора (SCA), а также локальным максимумам kh (положительная величина);
тальвеги соответствуют локальным: минимумам высоты h, локальным максимумам SCA, а также локальным минимумам kh (отрицательная величина).
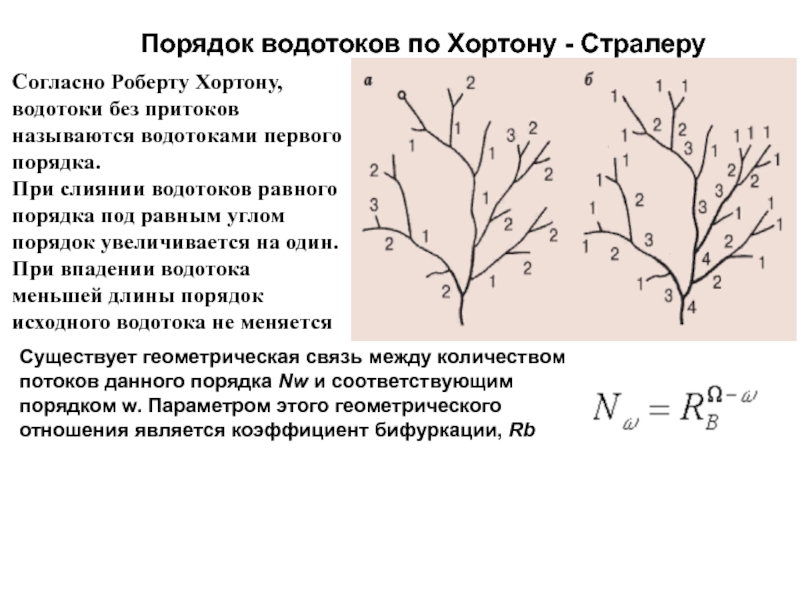
Слайд 73Порядок водотоков по Хортону - Стралеру
Согласно Роберту Хортону, водотоки без
притоков
называются водотоками первого порядка.
При слиянии водотоков равного порядка под равным
углом порядок увеличивается на один.При впадении водотока меньшей длины порядок исходного водотока не меняется
Существует геометрическая связь между количеством
потоков данного порядка Nw и соответствующим
порядком w. Параметром этого геометрического
отношения является коэффициент бифуркации, Rb
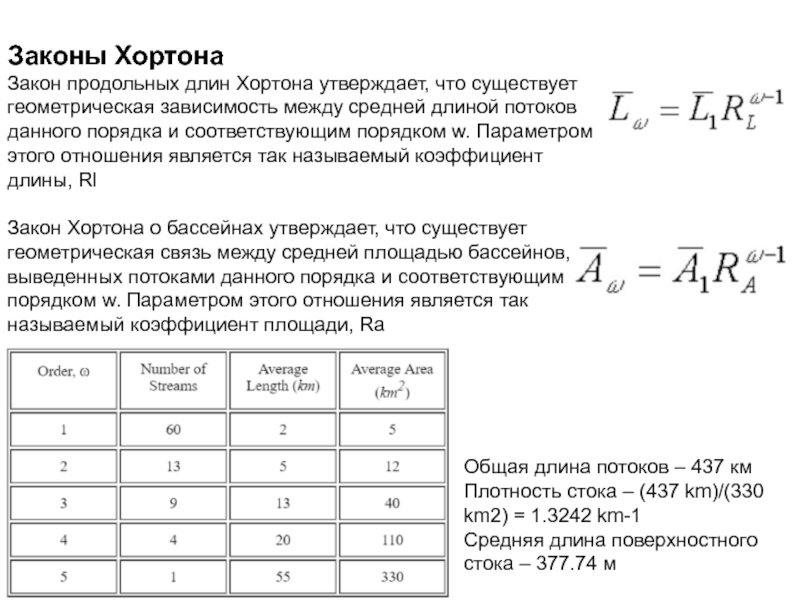
Слайд 74Законы Хортона
Закон продольных длин Хортона утверждает, что существует геометрическая зависимость
между средней длиной потоков данного порядка и соответствующим порядком w.
Параметром этого отношения является так называемый коэффициент длины, RlЗакон Хортона о бассейнах утверждает, что существует геометрическая связь между средней площадью бассейнов, выведенных потоками данного порядка и соответствующим порядком w. Параметром этого отношения является так называемый коэффициент площади, Rа
Общая длина потоков – 437 км
Плотность стока – (437 km)/(330
km2) = 1.3242 km-1
Средняя длина поверхностного
стока – 377.74 м
Слайд 75Закон Токунага
Модель Токунаги рассчитывает количество боковых притоков на реке одного
порядка
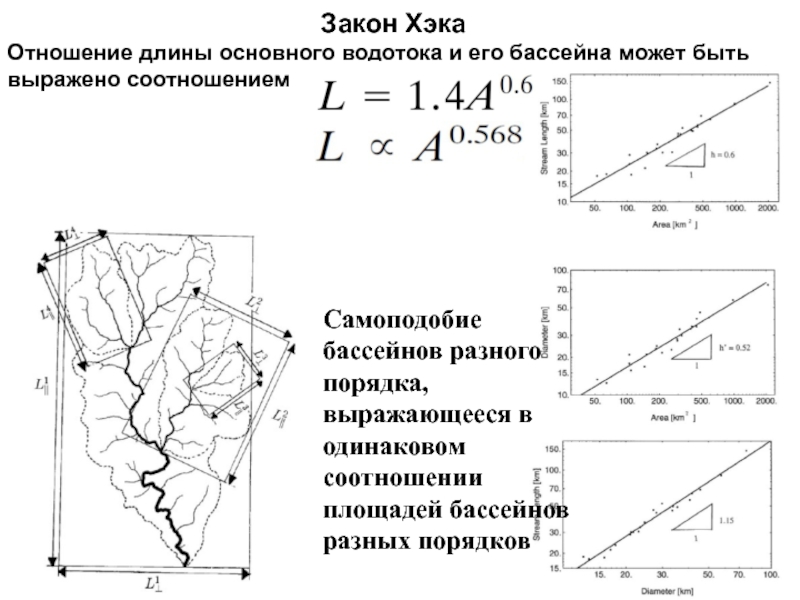
Слайд 76Самоподобие
бассейнов разного
порядка,
выражающееся в
одинаковом
соотношении
площадей бассейнов
разных порядков
Закон Хэка
Отношение длины основного водотока и
его бассейна может быть выражено соотношением
Слайд 77Автоматизированная процедура выделения водотоков длиннее заданной критической величины (блок TauDem
в MapWindow GIS).
Слайд 79Критерии точности моделирования
Ошибки и доля верно отображённых каналов учитываются интегральным
критерием F, равным отношению площади окрестностей выделенных моделью реальных водотоков
(S) и совокупной площади окрестностей реальных (SR) и модельных (SM) водотоков:Слайд 80Значения критерия точности F моделей дренажных сетей,
построенных методами классификации
кривизн, площади водосбора и эродирующей силы для ЦМР с различной
величиной пикселяСлайд 81Структура водотоков ЦЛГБПЗ. Расчет по ЦМР, критический параметр
удельная площадь водосбора
( SCA - specific catchment's area)
Структура
водосборных
геосистем
верховий р. Межа
Слайд 82Связь параметров гидрологического функционирования со структурой геосистем ЦЛГБПЗ
Зависимость средней площади
водосбора (Y) от его порядка (X) имеет вид
Y=b0*X**b1;
значения
параметров: b0=0.42, b1=2.52; достоверность модели R2=0.99977. Слайд 83Выделение бассейнов по удельной площади водосборов (блок TauDem в MapWindow
GIS).
1 - лесные заболоченные водосборы р Лонинка и Чернушка.
При их слиянии водосборная геосистема приобретает 3-ий порядок и целиком находится в пределах ландшафта озерно-водно-ледниковой равнины с грядами.2 - границы водосборных геосистем 1-го порядка.
Слайд 84Q – расход, м3/с;
- площадь живого сечения, м2;
R –
гидравлический радиус, м, R=/;
- смоченный периметр, м;
с – коэффициент
Шези;n – коэффициент шероховатости русла (принимается по справочникам в зависимости от состояния русла);
i – уклон свободной поверхности (для большинства равнинных рек 0,001…0,005)
5. ГИДРАВЛИЧЕСКИЙ МЕТОД ВЫЧИСЛЕНИЯ РАСХОДОВ
применяется, если нет возможности измерить скорости течения, реализован в ряде ГИС с функциями расчета параметров водосборов, в частности в ГИС SAGA
Формула Шези-Маннинга
Слайд 85Распределение гидрофизических
параметров на основе структуры ландшафтов бассейна р. Лонинка
для моделирования
гидрологи-ческих процессов в ГИС SAGA.
А -
Manning’s n B - Curve number,
А
В


![Географический факультет Московского государственного университета им Направления исследования ландшафтоведения [К.Н.Дьяконов, 2004]структурно-генетическоеструктурно-функциональноефункционально-динамическое геофизическоегеохимическоесоциальный ландшафтогенезпалеоландшафтноеландшафтная экологияландшафтное планирование геоэкологическое эволюционное физико-математическое Направления исследования ландшафтоведения [К.Н.Дьяконов, 2004]структурно-генетическоеструктурно-функциональноефункционально-динамическое геофизическоегеохимическоесоциальный ландшафтогенезпалеоландшафтноеландшафтная экологияландшафтное планирование геоэкологическое эволюционное физико-математическое (сквозное), ПРЕДМЕТОМ КОТОРОГО ЯВЛЯЕТСЯ](/img/thumbs/9f5b9d7833c5d27e5878a85c43a9c968-800x.jpg)








![Географический факультет Московского государственного университета им Систематизация уровней почвенных структур по масштабной шкале [Шеин, 2005] Систематизация уровней почвенных структур по масштабной шкале [Шеин, 2005]](/img/thumbs/464d1fa50daaa35757c82815c9aef9a9-800x.jpg)







![Географический факультет Московского государственного университета им Классы морфометрических величин и понятий [Шарый, 1995]. 2. ВЫБОР ПАРАМЕТРОВ ПРОСТРАНСТВЕННОЙ СТРУКТУРЫ ГЕОСИСТЕМ Классы морфометрических величин и понятий [Шарый, 1995]. 2. ВЫБОР ПАРАМЕТРОВ ПРОСТРАНСТВЕННОЙ СТРУКТУРЫ ГЕОСИСТЕМ](/img/thumbs/eabbbf5918404dbdec4e8a487fe2863b-800x.jpg)
![Географический факультет Московского государственного университета им Формулы расчета локальных морфометрических величин [Shary, 1995]. ( p=z/x; q=z/y; r=2z/x2; s=2z/xy; t=2z/y2, z=z(x,y)). Формулы расчета локальных морфометрических величин [Shary, 1995]. ( p=z/x; q=z/y; r=2z/x2; s=2z/xy; t=2z/y2, z=z(x,y)).](/img/thumbs/70dbcab584d8eca88ee9a3026b8ec032-800x.jpg)

![Географический факультет Московского государственного университета им К ОПИСАНИЮ ДВУХ ОСНОВНЫХ МЕХАНИЗМОВ АККУМУЛЯЦИИ [ШАРЫЙ,1991]. Слева – первый механизм К ОПИСАНИЮ ДВУХ ОСНОВНЫХ МЕХАНИЗМОВ АККУМУЛЯЦИИ [ШАРЫЙ,1991]. Слева – первый механизм аккумуляции, сближение потоков; второй механизм аккумуляции](/img/thumbs/23c929a80e9d6833b1eba0c3405dd72c-800x.jpg)