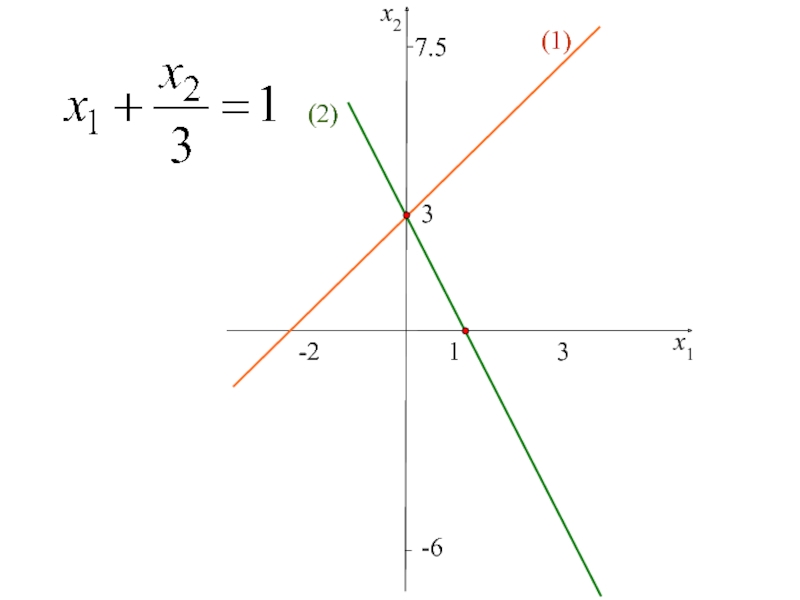
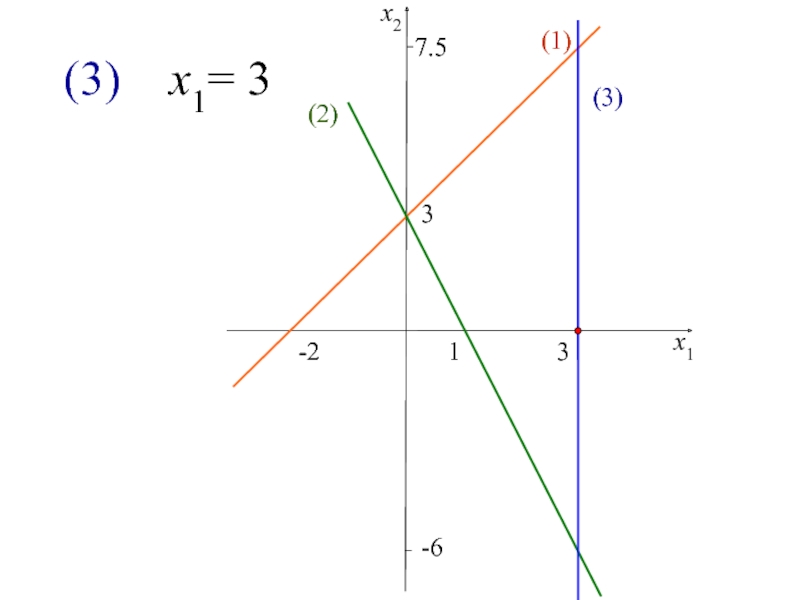
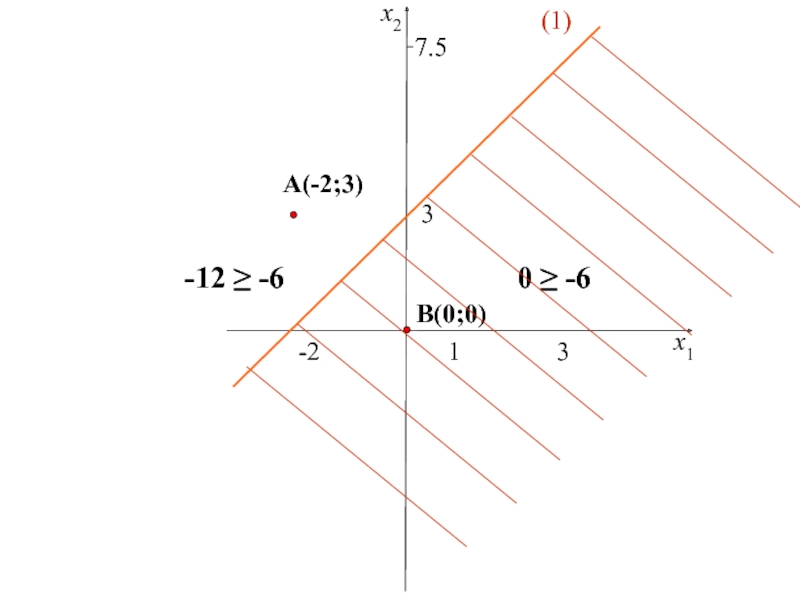
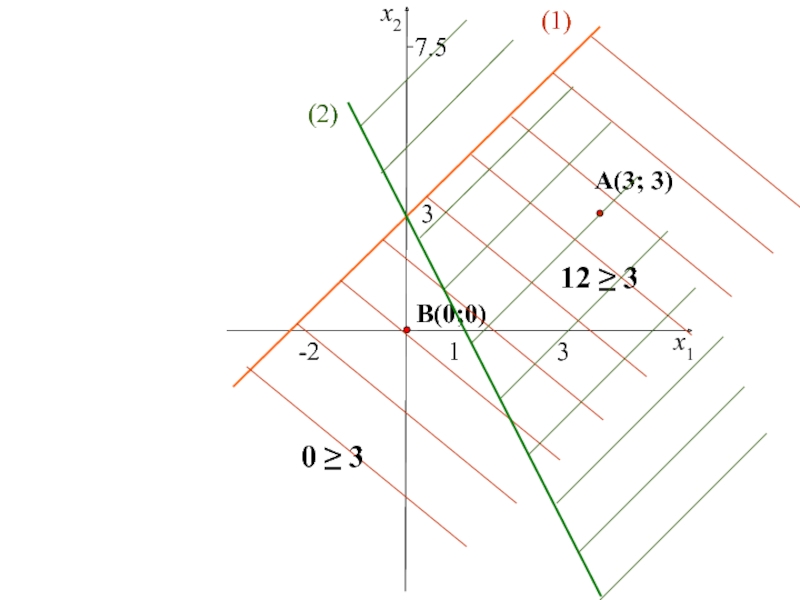
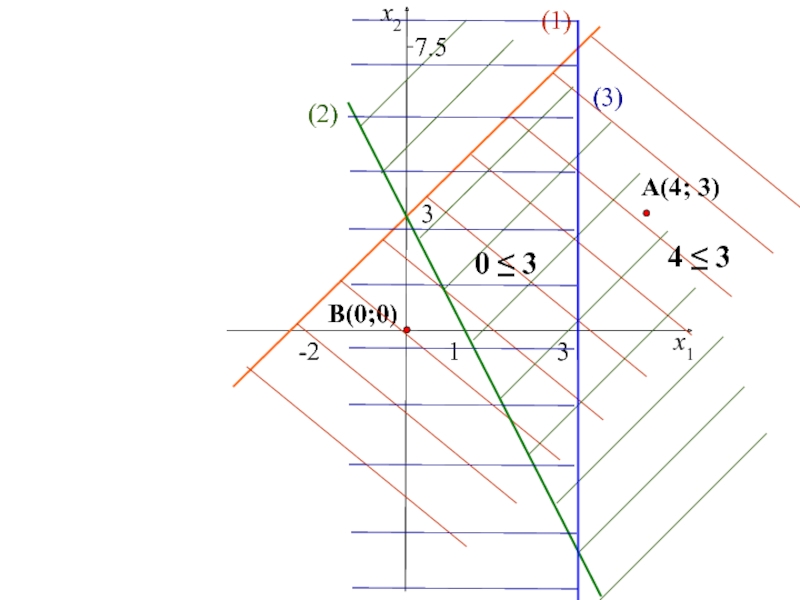
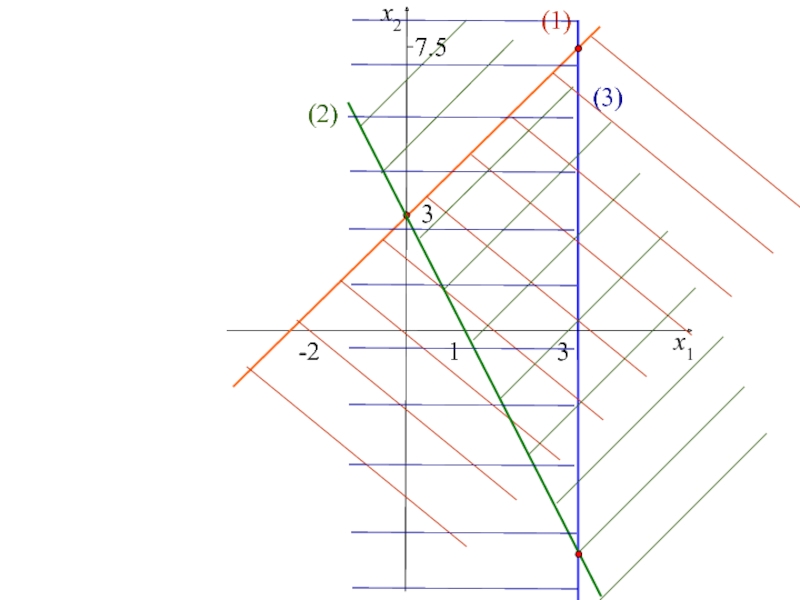
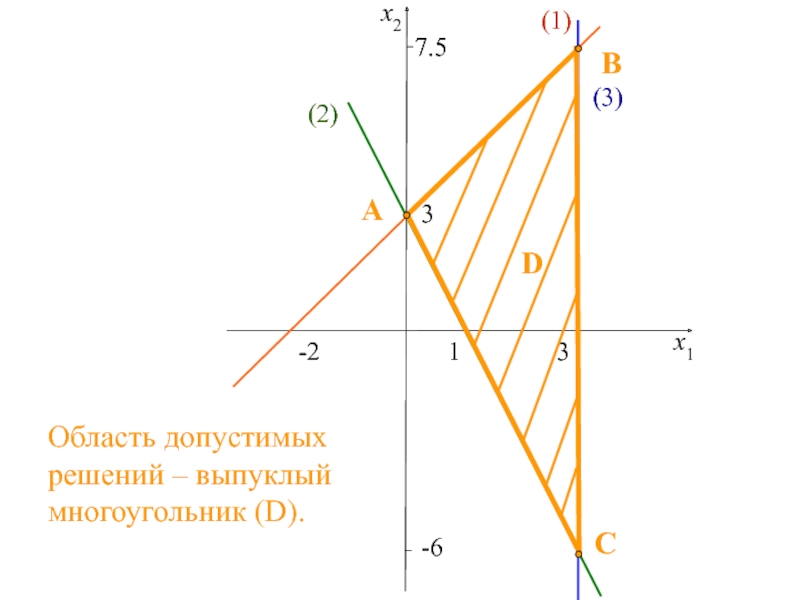
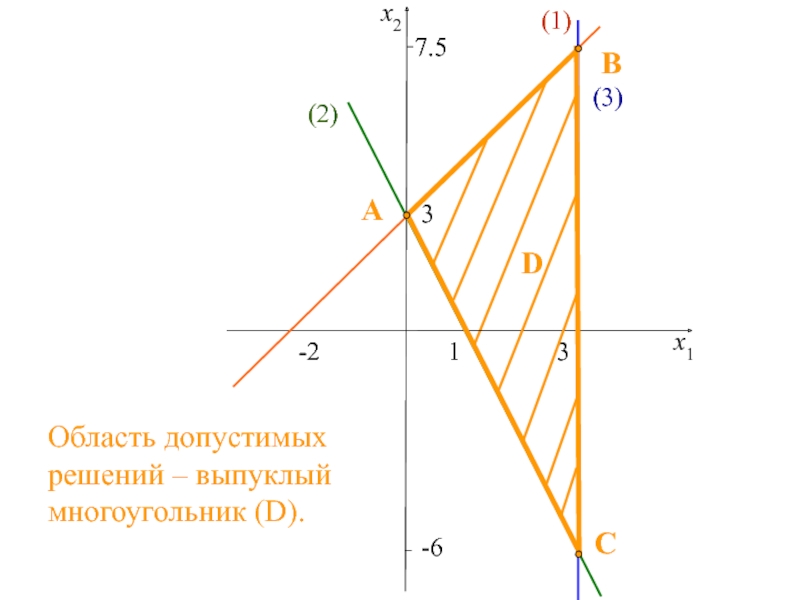
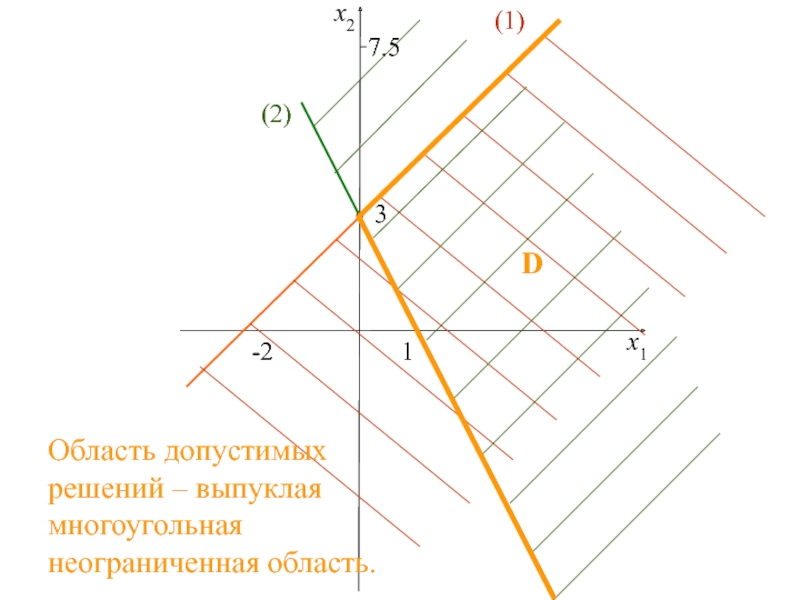
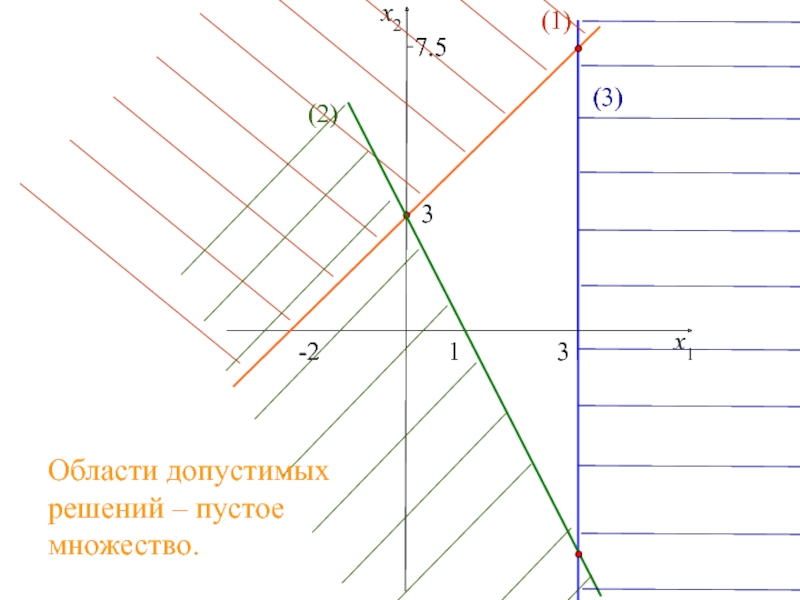
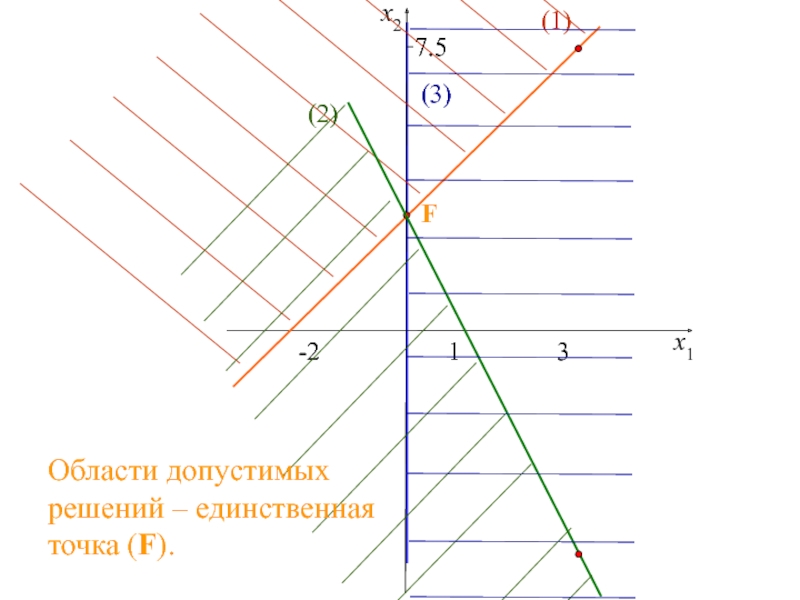
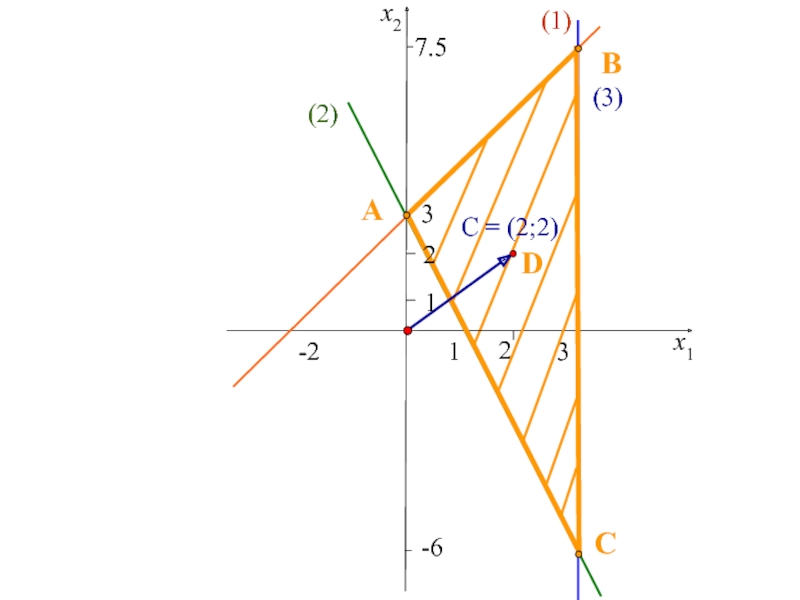
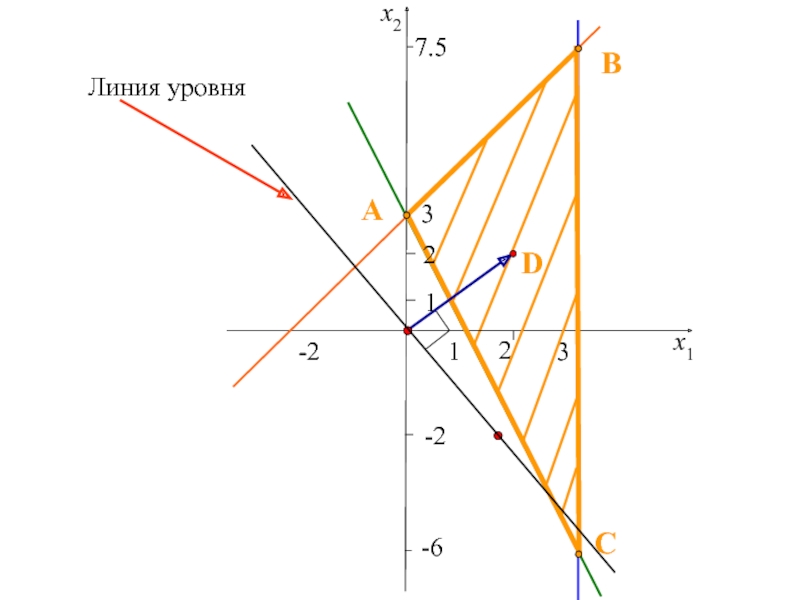
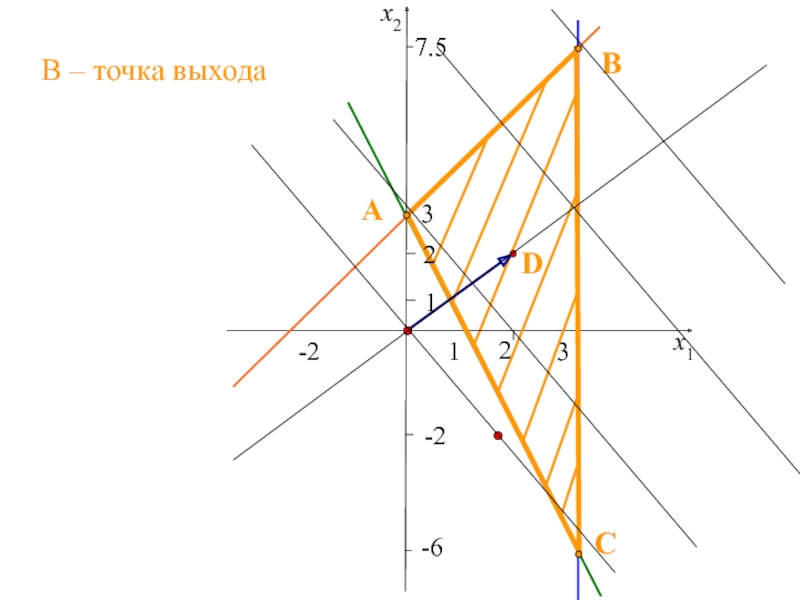
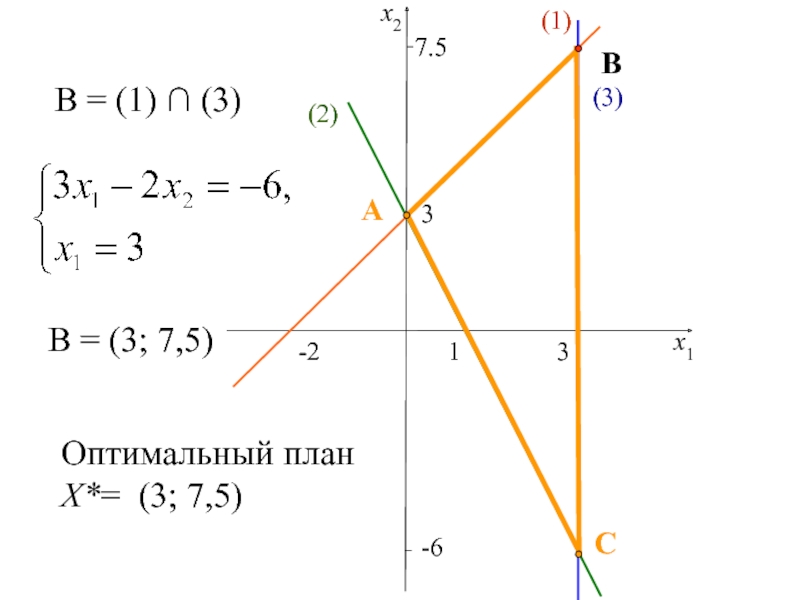
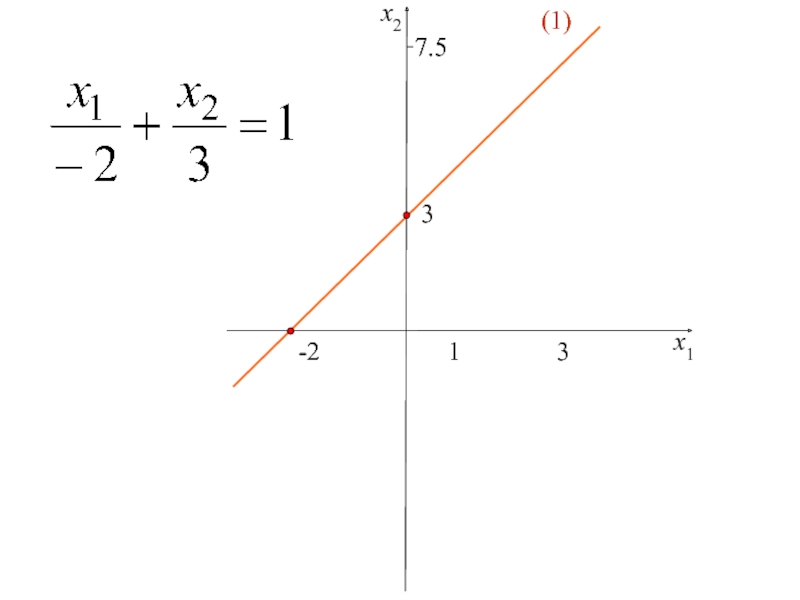двух переменных,
задачи, заданные в канонической форме, с числом свободных переменных
,задачи, в произвольной форме записи, которые после приведения к канонической форме будут содержать не более двух свободных переменных .