Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
ГИА 9 Методика решений заданий и оформление второй части
Содержание
- 1. ГИА 9 Методика решений заданий и оформление второй части
- 2. Найти все значения k, при которых прямая
- 3. Найти все значения k, при которых прямая
- 4. Л.В. Кузнецова и др. № 5.34. При
- 5. Л.В. Кузнецова и др. № 2.59. При
- 6. Л.В. Кузнецова и др. № 5.39. При
- 7. Задачи на « концентрацию», « смеси и
- 8. Задачи на « концентрацию», « смеси и
- 9. Задачи на « концентрацию», « смеси и
- 10. Задачи на « концентрацию», « смеси и
- 11. Задачи на « концентрацию», « смеси и
- 12. ПрогрессииКузнецова Л.В. № 6.30 (2). Решите уравнение:1.
- 13. ПрогрессииКузнецова Л.В. № 6.28 (1). Найти
- 14. Наименьшее и наибольшее значениеКузнецова Л.В. № 2.62.
- 15. Наименьшее и наибольшее значение
- 16. Скачать презентанцию
Слайды и текст этой презентации
Слайд 2Найти все значения k, при которых прямая y = kx
пересекает в одной точке ломаную, заданную условием:
1) Построим ломаную.
y
= - 2x, у = 2, у = 3 х – 4 Выделим указанные участки этих прямых.
2) Прямая y = kx проходит через начало координат.
Функции и графики
Слайд 3Найти все значения k, при которых прямая y = kx
пересекает в одной точке ломаную, заданную условием.
Прямая y = kx
проходит через начало координат.Рассмотрим различные случаи расположения этих графиков.
Ж м
Прямая у = х пересекает ломаную в одной точке (2;2).
При k = - 2 – прямая и ломаная имеют бесконечное множество общих точек.
Если k ≥ 3 и k < - 2, то прямая у = kx пересекает ломаную в одной точке.
Остальные значения k не удовлетворяют условию.
Ответ:
Или k < -2, k = 1, k ≥ 3.
Функции и графики
Слайд 4Л.В. Кузнецова и др. № 5.34. При каких значениях p
вершины парабол y = x2 – 2px – 1 и
y = - x2 + 4px + p расположены по разные стороны от оси Ох?Найдем координаты вершин парабол.
y = x2 – 2px – 1: хв = p; yв = - 1 – р2.
y = - x2 + 4px + p: хв = 2р; ув = 4р2 + р.
Т.к. вершины расположены по разные стороны от оси Ох, то ординаты вершин должны иметь разные знаки.
- р2 – 1 < 0, то 4р2 + р > 0
p (4p +1) > 0
p
- ¼
0
+
-
+
Ответ: р < - 0,25; p > 0.
или
Функции и графики
Слайд 5Л.В. Кузнецова и др. № 2.59. При каких значениях а
один корень квадратного уравнения x2 – (a + 1)x +
2a2 = 0 больше ½, а другой меньше ½?Введем функцию f(x) = x2 – (a + 1)x + 2a2.
Графиком этой функции является парабола ветви которой направлены вверх. Нули функции должны быть расположены по разные стороны от числа ½.
Значит f(½) < 0.
2а2 - ½ (а + 1) + ¼ < 0
2a2 - ½ a - ¼ < 0
8a2 – 2a – 1 <0
Ответ: - ¼ < а < ½
Функции и графики
Слайд 6Л.В. Кузнецова и др. № 5.39. При каких значениях р
прямая у = 0,5х + р образует с осями координат
треугольник площадь которого равна 81? Прямая у = 0,5х + р параллельна прямой у = 0,5х и пересекает оси координат в точках (0; р) и (- 2р; 0)
ΔАОВ – прямоугольный.
Ответ: р = - 9; р = 9.
Функции и графики
Слайд 7Задачи на « концентрацию», « смеси и сплавы».
масса смеси
( сплава);
концентрация ( доля чистого вещества в смеси);
количество
чистого вещества в смеси ( сплаве). Масса смеси х концентрация = количество вещества
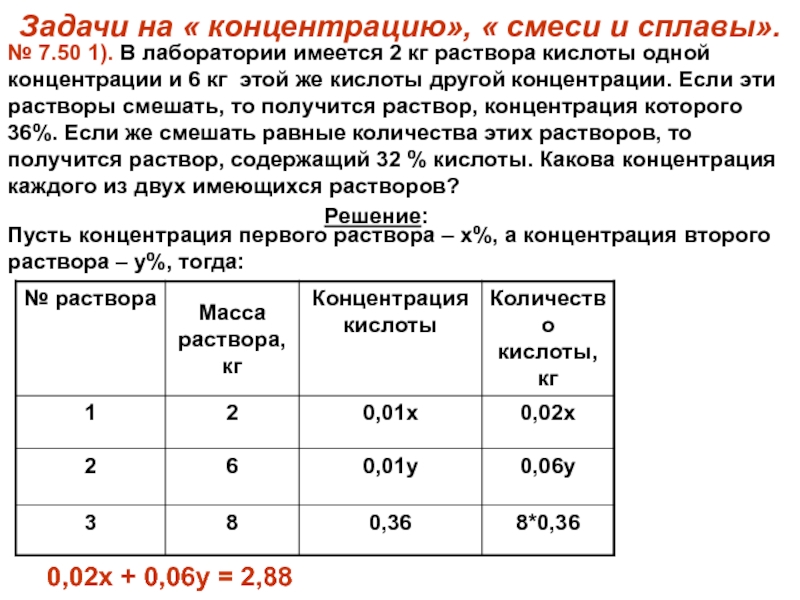
Слайд 8Задачи на « концентрацию», « смеси и сплавы».
№ 7.50 1).
В лаборатории имеется 2 кг раствора кислоты одной концентрации и
6 кг этой же кислоты другой концентрации. Если эти растворы смешать, то получится раствор, концентрация которого 36%. Если же смешать равные количества этих растворов, то получится раствор, содержащий 32 % кислоты. Какова концентрация каждого из двух имеющихся растворов?Решение:
Пусть концентрация первого раствора – х%, а концентрация второго раствора – у%, тогда:
0,02х + 0,06у = 2,88
Слайд 9Задачи на « концентрацию», « смеси и сплавы».
0,01х + 0,01у
= 0,64
Примем за 1 одинаковую массу растворов, тогда:
Решим систему уравнений:
Ответ:
Концентрация первого раствора – 24%,концентрация второго раствора – 40%.
Слайд 10Задачи на « концентрацию», « смеси и сплавы».
№ 7.49 1).
В свежих яблоках 80% воды, а сушеных – 20%. На
сколько процентов уменьшается масса яблок при сушке?Решение:
х = 0,8 – 0,2(1 – х)
Примем за 1 массу свежих яблок и пусть масса яблок при сушке уменьшится на х кг, тогда имеем:
При сушке потеря массы яблок происходит за счет потери массы воды. Имеем уравнение:
х = 0,6 + 0,2х
0,8х = 0,6
х = 0,75.
Яблоки при сушке теряют 0,75 от своей массы, т. е. 75%.
Ответ: 75%.
Слайд 11Задачи на « концентрацию», « смеси и сплавы».
№ 7.51 1).
При смешивании первого раствора кислоты, концентрация которого 20%, и второго
раствора этой же кислоты, концентрация которого 50%, получили раствор, содержащий 30% кислоты. В каком отношении были взяты 1 и 2 растворы?Решение:
Пусть масса первого раствора – х, а масса второго раствора – у, тогда:
0,2х + 0,5у = 0,3(х + у)
Количество кислоты в смеси складывается из количества кислоты первого и второго растворов, поэтому имеем уравнение:
2х + 5у = 3х + 3у,
2у = х,
х : у = 2 : 1
Ответ: первый и второй растворы взяты в отношении 2 : 1.
Слайд 12Прогрессии
Кузнецова Л.В. № 6.30 (2). Решите уравнение:
1. Рассмотрим последовательность (ап):
а3
- а2 = а2 - а1 = - 1/х2 =
d( ап ) – арифметическая
прогрессия по определению.
Х = 15.
Ответ: х = 15.
Слайд 13Прогрессии
Кузнецова Л.В. № 6.28 (1).
Найти сумму первых 20
совпадающих членов двух арифметических прогрессий: 3, 8, 13,
… и 4, 11, 18,..d1 = 5 d2 =7.
Решение 1.Пусть (ап) –последовательность совпадающих
членов арифметических прогрессий, тогда она тоже
является арифметической прогрессией с разностью d.
НОК (d1, d2) = 35 = d. Первый совпадающий член равен 18,
n =20, то
Решение 2. Рассмотрим прогрессии:
3, 8, 13, 18, 23, 28, 33, 38, 43, 48, 53,…
4, 11, 18, 25, 32, 39, 46, 53… Далее решение №1.
Возможна вычислительная ошибка!
Слайд 14Наименьшее и наибольшее значение
Кузнецова Л.В. № 2.62. Докажите, что уравнение
не имеет корней.
1. Рассмотрим функции: а)
- которая принимает наименьшее значение равное 1 при х = -1б)
которая принимает наименьшее
значение равное 1, при х = 2.
2. Произведение двух множителей равно 1 тогда и только тогда, когда каждый из них равен 1, либо множители принимают взаимно – обратные значения.
3.Т.к. наименьшее значение равно 1, взаимно – обратными
они быть не могут .
4. Каждый из них равен 1 при различных значениях х,
т.е. одновременно они не могут быть равны 1.
Ответ: Уравнение не имеет корней.