ГЛАВА 26. ПЛАВАНИЕ ПО ДУГЕ БОЛЬШОГО КРУГА – ОРТОДРОМИИ

ПО ДУГЕ БОЛЬШОГО КРУГА – ОРТОДРОМИИ
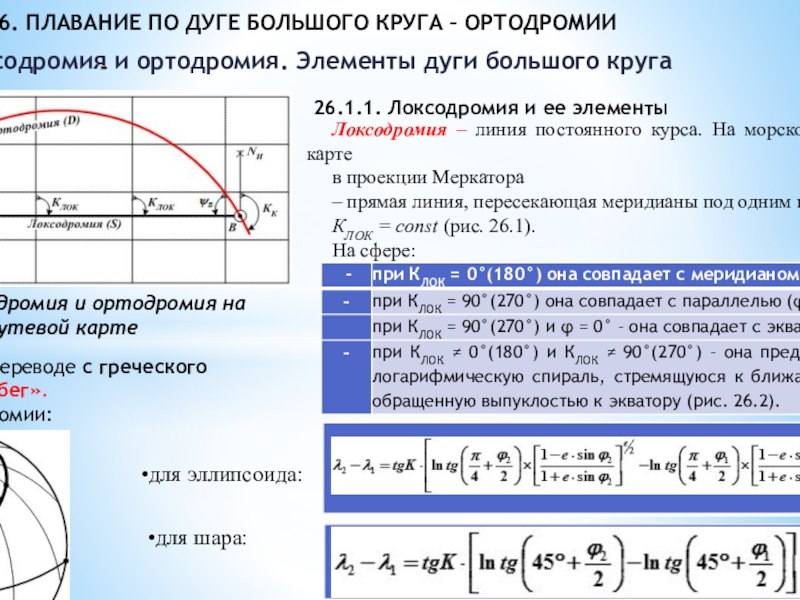
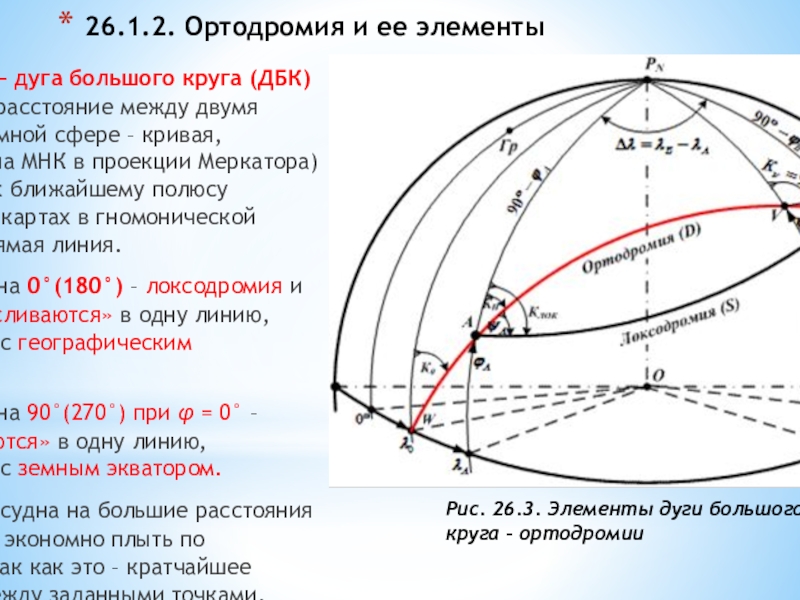
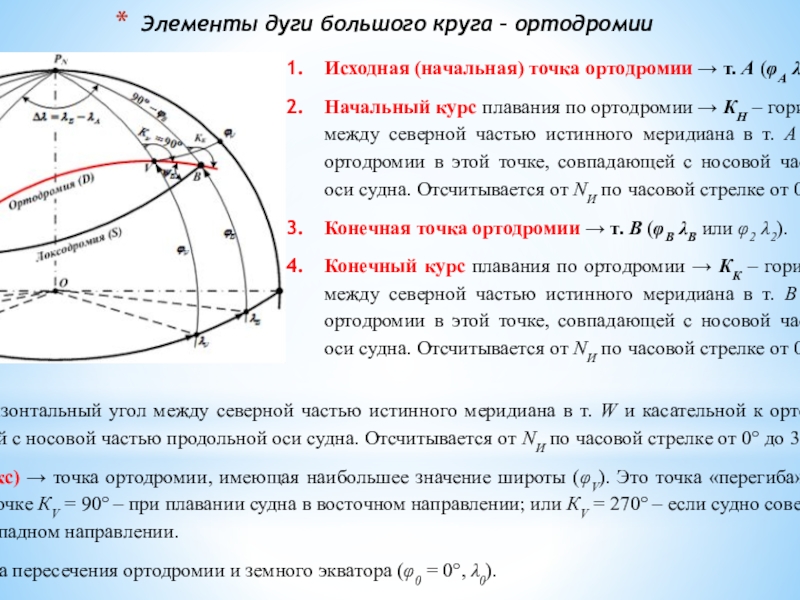
Рис. 26.1. Локсодромия и ортодромия

на меркаторской путевой карте

26.1.1. Локсодромия и ее элементы

Локсодромия – линия постоянного курса. На морской навигационной карте
в проекции Меркатора
– прямая линия, пересекающая меридианы под одним и тем же углом
КЛОК = const (рис. 26.1).
На сфере:

Локсодромия в переводе с греческого означает «косой бег».
Формула локсодромии:

для эллипсоида:

для шара:

При плавании судна на небольшие расстояния (сотни миль) и ведении графического счисления пути судна на карте в проекции Меркатора удобно выполнять это плавание по локсодромии – линии постоянного курса, несмотря на то, что это и не кратчайшее расстояние между двумя заданными точками.

– кратчайшее расстояние между двумя точками на земной сфере –

кривая, обращенная (на МНК в проекции Меркатора) выпуклостью к ближайшему полюсу (рис.26.1). На картах в гномонической проекции – прямая линия.
При курсе судна 0°(180°) – локсодромия и ортодромия «сливаются» в одну линию, совпадающую с географическим меридианом.
При курсе судна 90°(270°) при φ = 0° – также «сливаются» в одну линию, совпадающую с земным экватором.
При плавании судна на большие расстояния (тысячи миль) экономно плыть по ортодромии, так как это – кратчайшее расстояние между заданными точками.

Рис. 26.3. Элементы дуги большого круга – ортодромии

т. А (φА λА или φ1 λ1).
Начальный курс плавания по

ортодромии → КН – горизонтальный угол между северной частью истинного меридиана в т. А и касательной к ортодромии в этой точке, совпадающей с носовой частью продольной оси судна. Отсчитывается от NИ по часовой стрелке от 0° до 360°.
Конечная точка ортодромии → т. В (φВ λВ или φ2 λ2).
Конечный курс плавания по ортодромии → КК – горизонтальный угол между северной частью истинного меридиана в т. В и касательной к ортодромии в этой точке, совпадающей с носовой частью продольной оси судна. Отсчитывается от NИ по часовой стрелке от 0° до 360°.

5. Курс К0 → горизонтальный угол между северной частью истинного меридиана в т. W и касательной к ортодромии в этой точке, совпадающей с носовой частью продольной оси судна. Отсчитывается от NИ по часовой стрелке от 0° до 360°.
6. Точка V (вертекс) → точка ортодромии, имеющая наибольшее значение широты (φV). Это точка «перегиба» ортодромии и курс судна в этой точке КV = 90° – при плавании судна в восточном направлении; или КV = 270° – если судно совершает плавание по ортодромии в западном направлении.
7. Точка W → точка пересечения ортодромии и земного экватора (φ0 = 0°, λ0).

треугольник ортодромии
Из сферической тригонометрии известно «…если в сферическом треугольнике известны

три элемента то, по формулам сферической тригонометрии, можно определить и все остальные…».
Применяя формулу «косинуса стороны» («…косинус стороны равен произведению косинусов двух других сторон плюс произведение синусов тех же сторон на косинус угла между ними…») можно определить длину ортодромии (D) между любыми двумя ее точками (т. А и т. В), координаты которых известны, то есть:
cosD = cos(90° − φA) · cos(90° − φB) + sin(90° − φA) · sin(90° − φB) · cos(λB – λA)

на синус среднего угла равно произведению котангенса крайней стороны на

синус средней стороны минус произведение косинусов средних частей…») можно определить значение начального КH и конечного КK курсов плавания по ортодромии.

Аналогично определяем остальные величины:

или