Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Глобальная динамическая модель Форрестера
Содержание
- 1. Глобальная динамическая модель Форрестера
- 2. Джей Форрестер (14.07.1918 – 16.11.2016) - американский инженер и системолог, разработчик теории системной динамики
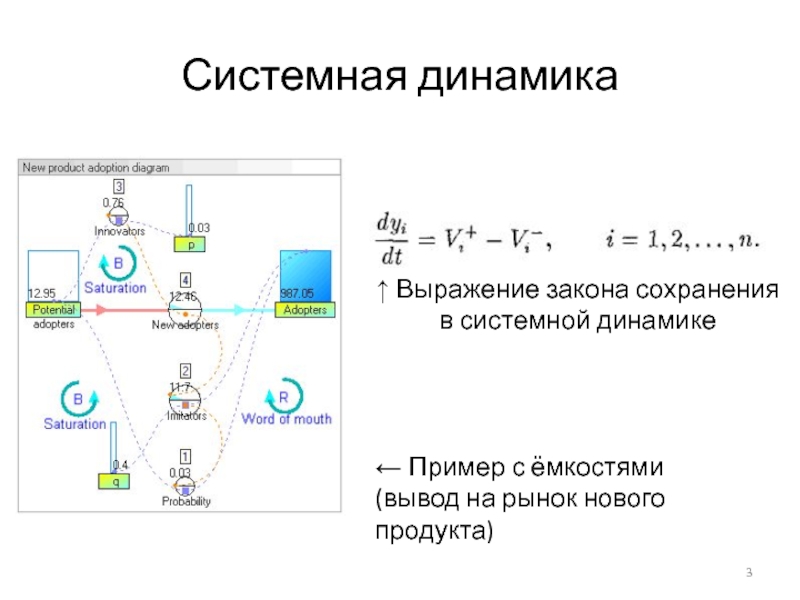
- 3. Системная динамика↑ Выражение закона сохранения в системной динамике← Пример с ёмкостями(вывод на рынок нового продукта)
- 4. Этапы моделирования сложной системыПостановка задачи (концептуализация);Математическое описание модели системы;Анализ модели.
- 5. Постановка задачиПодробное словесное описание сложной системы →
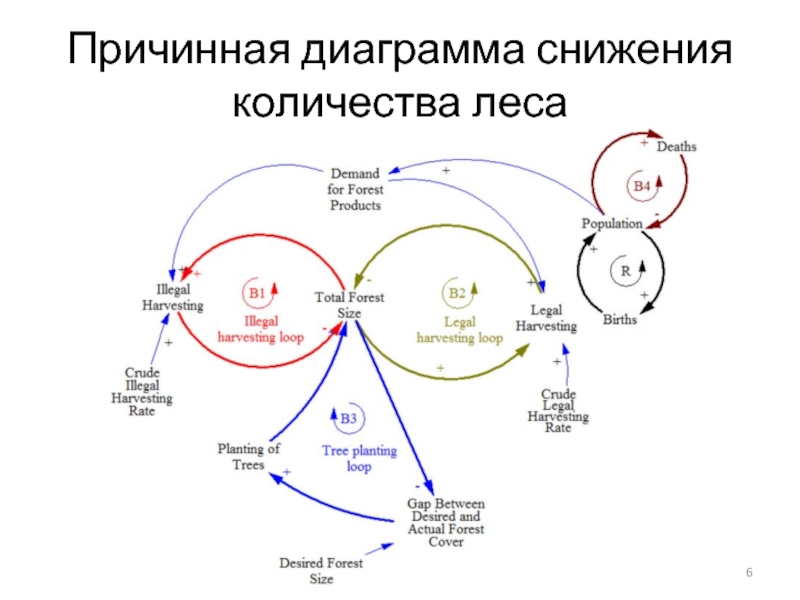
- 6. Причинная диаграмма снижения количества леса
- 7. Математическое описание модели системыПричинная диаграмма → потоковая
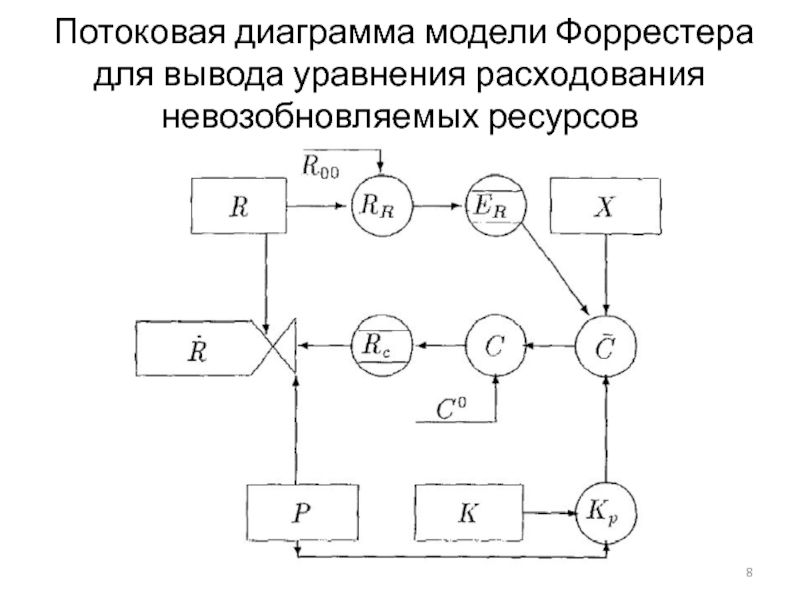
- 8. Потоковая диаграмма модели Форрестера для вывода уравнения расходования невозобновляемых ресурсов
- 9. Анализ моделиРасчёт уравнений на ЭВМ → сравнение
- 10. Система уравнений модели ФоррестераP – население; B
- 11. Уравнение демографического сектораКонстанты СВ и СD –
- 12. Уравнение капиталаСk - начальная скорость генерации капиталовложений
- 13. Уравнение с/х сектораFp – уровень питания, XF
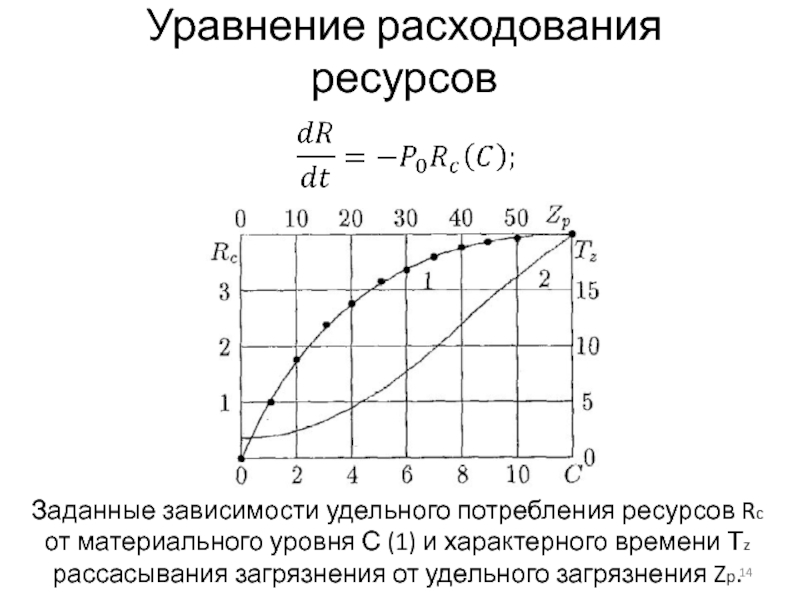
- 14. Уравнение расходования ресурсовЗаданные зависимости удельного потребления ресурсов
- 15. Уравнение уровня загрязненияZ0 – постоянная нормальная скорость
- 16. Начальные данныеt00 – 1900 г.;P00 – 1,65*10^9
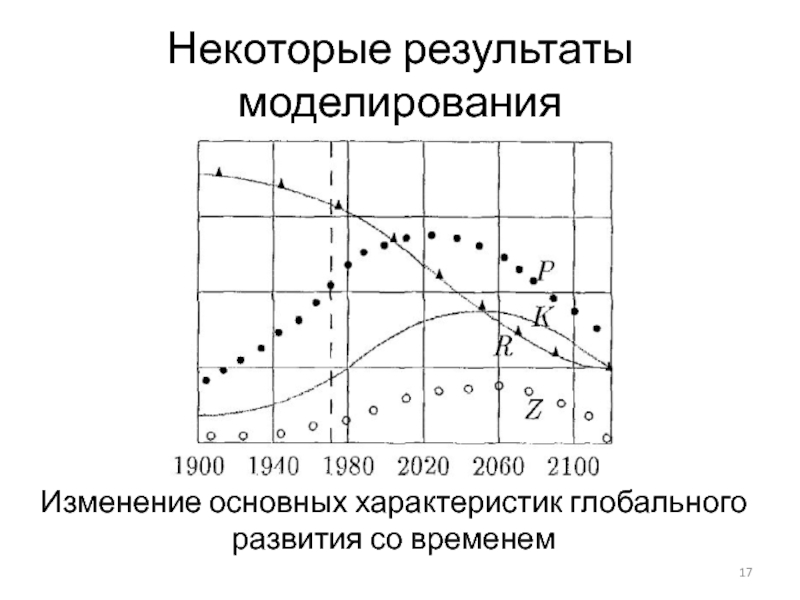
- 17. Некоторые результаты моделированияИзменение основных характеристик глобального развития со временем
- 18. Cписок используемой литературыБелолипецкий В.М., Шокин Ю.И. Математическое
- 19. Скачать презентанцию
Джей Форрестер (14.07.1918 – 16.11.2016) - американский инженер и системолог, разработчик теории системной динамики