Слайд 1Графические возможности Matlab
Лекция 4
Слайд 2Графика в Matlab
Высокоуровневая
не требует от пользователя детальных знаний о
работе графической подсистемы
Объектная
каждый объект на рисунке имеет свойства, которые можно
менять
Управляемая (handled)
доступ к графическим объектам возможен как через инспектор объектов, так и при помощи встроенных функций (дескрипторная графика)
Слайд 3Построение графиков функции одной переменной
Простейший способ построения 2D-графика:
Задать область построения
(диапазон).
Вычислить значение функции на области построения.
Построить график при помощи одной
из встроенных функций Matlab.
Слайд 5Построение второго графика
Если сразу же построить другой график, то старый
график будет удалён из графического окна
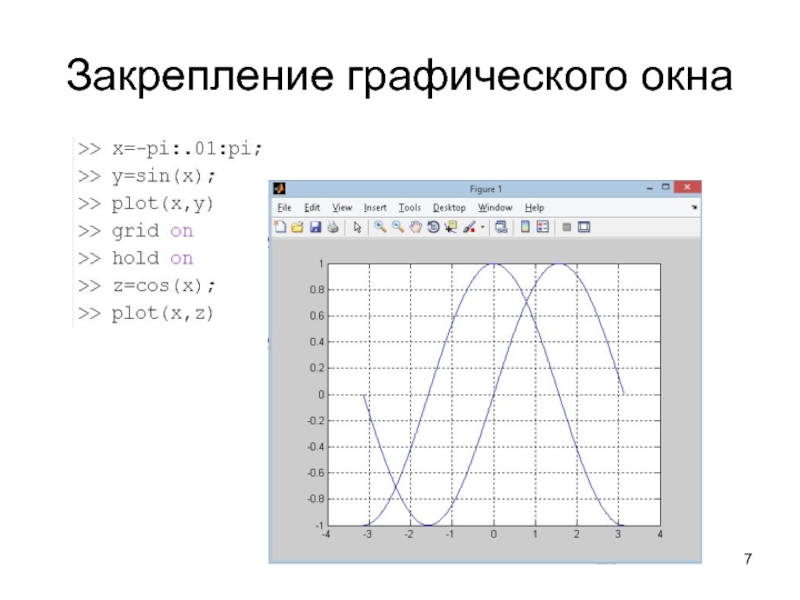
Слайд 6Построение двух графиков в одной системе координат
Два графика в одной
СК можно построить следующими способами:
«закрепить» графическое окно при помощи команды
hold on
применить одну команду plot
Слайд 7Закрепление графического окна
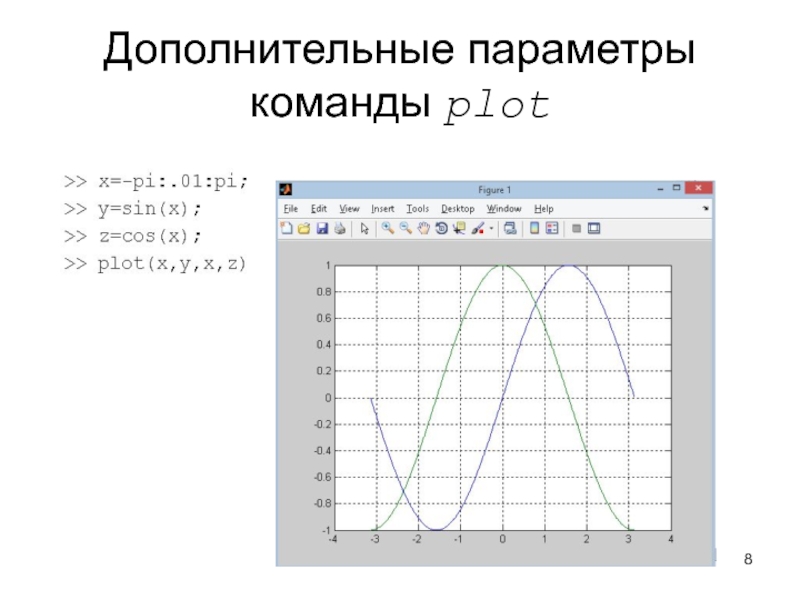
Слайд 8Дополнительные параметры команды plot
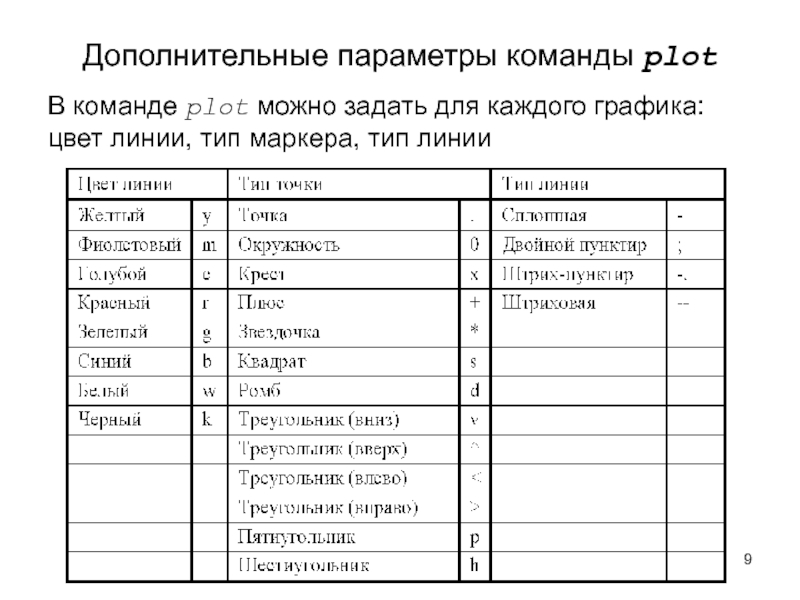
Слайд 9Дополнительные параметры команды plot
В команде plot можно задать для каждого
графика: цвет линии, тип маркера, тип линии
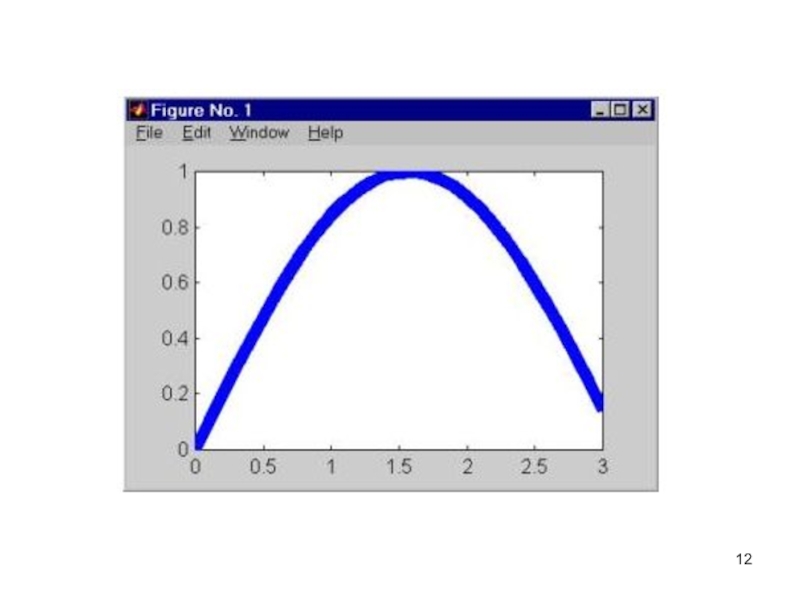
Слайд 11 Толщина линии указывается с помощью функции set.
Пример.
>>x =
0 : 0.1 : 3;
>>y = sin( x );
>>p =
plot( x, y );
>>set( p, 'LineWidth', 7 );
В примере свойство 'LineWidth' (толщина линии), для которого задали новое значение 7 пикселей (по умолчанию - 0.5 пикселей).
Допустима запись:
>>plot(x,y,'LineWidth‘,7)
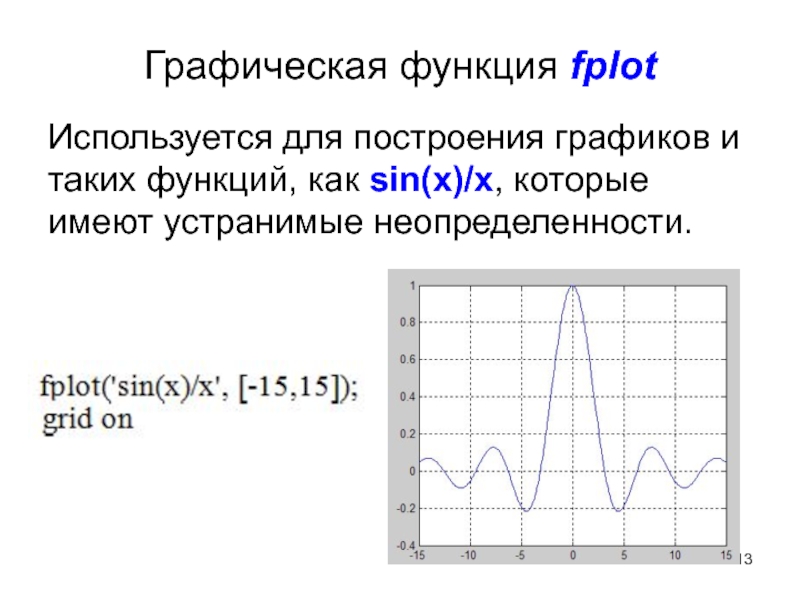
Слайд 13Графическая функция fplot
Используется для построения графиков и таких функций, как
sin(x)/x, которые имеют устранимые неопределенности.
Слайд 14Построение дискретных графиков
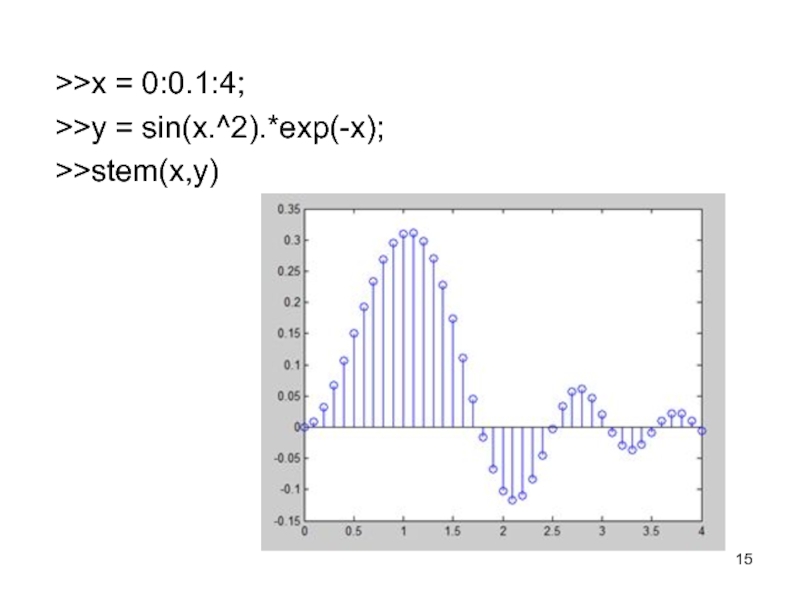
Такой график применяется, например, при описании квантования сигналов.
Каждый отсчет представляется вертикальной чертой, увенчанной кружком, причем высота черты
соответствует y- координате точки.
Для построения графика подобного вида используются команды stem(x,y):
Слайд 15>>x = 0:0.1:4;
>>y = sin(x.^2).*exp(-x);
>>stem(x,y)
Слайд 16Построение лестничных графиков
Лестничные графики представляют собой ступеньки с огибающей,
заданной в виде функции y(t). Они используются, например, для наглядного
представления функции y(t), представленной результатами ряда измерений ее значений. При этом в промежутках между измерениями значения функции считаются постоянными и равными величине последнего результата измерения.
Слайд 18Графики с логарифмическим масштабом
Встречаются случаи, когда диапазон
изменения
функции настолько велик, что
для ее графической визуализации
приходится применять
логарифмический и полулогарифмический масштаб.
Для построения графиков в
логарифмическом масштабе служат
следующие функции:
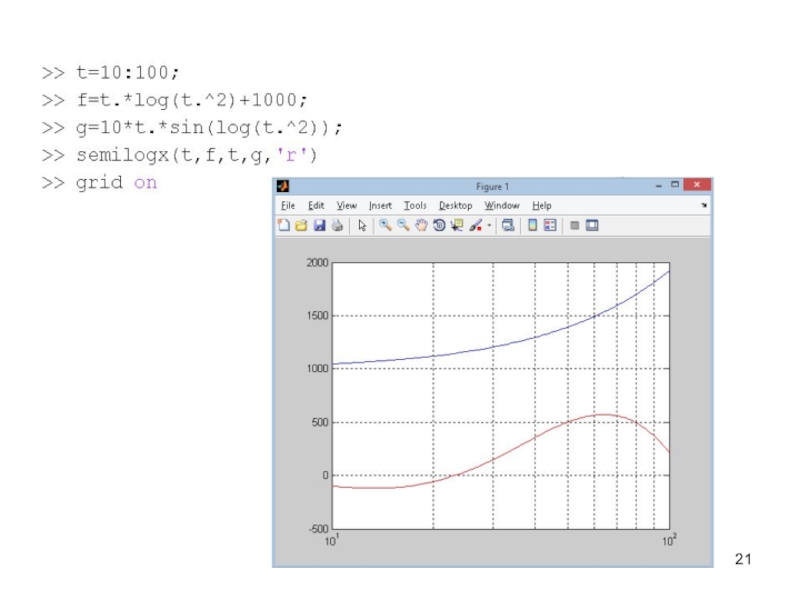
Слайд 19loglog(…) – логарифмический масштаб по обеим осям;
semilogx(…) – логарифмический
масштаб по оси абсцисс;
semilogy(…) – логарифмический масштаб по оси
ординат.
Аргументы этих функций (все, что стоит внутри скобок) формируются по тем же правилам, что и в функции plot(…).
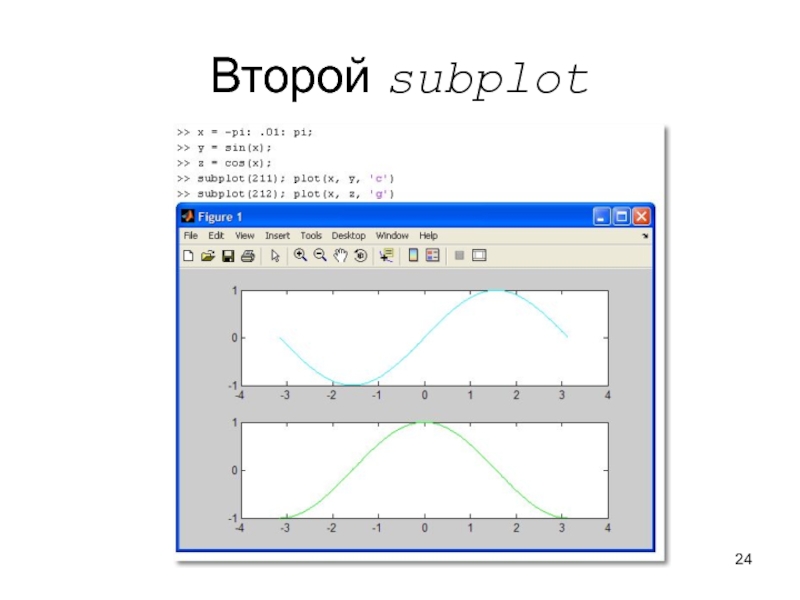
Слайд 22Построение нескольких графиков в одном окне в разных СК
Поверхность графического окна можно разделить на зоны, в каждой
из которых выводить свой график
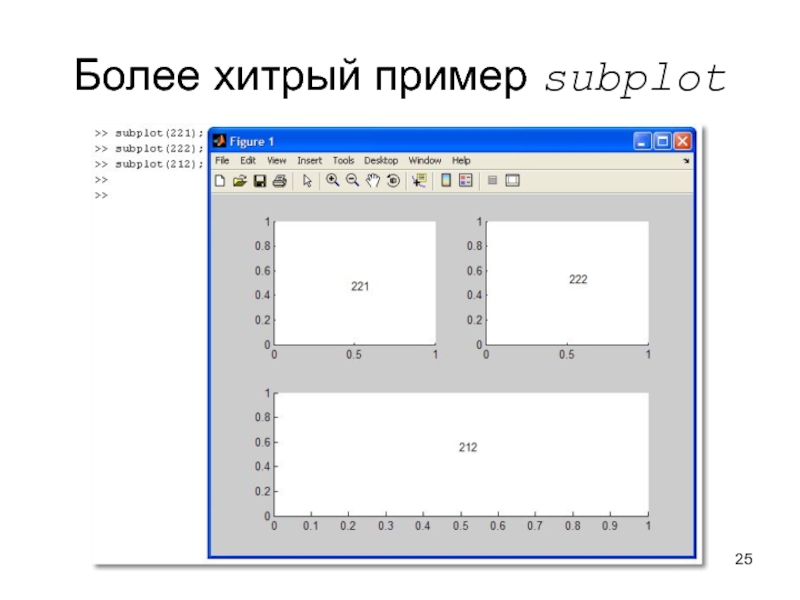
Для этого служит команда subplot(mnk)
m и n определяют количество графических «подокон» по горизонтали и вертикали
k задаёт номер графического «подокна»
порядок нумерации – по строкам
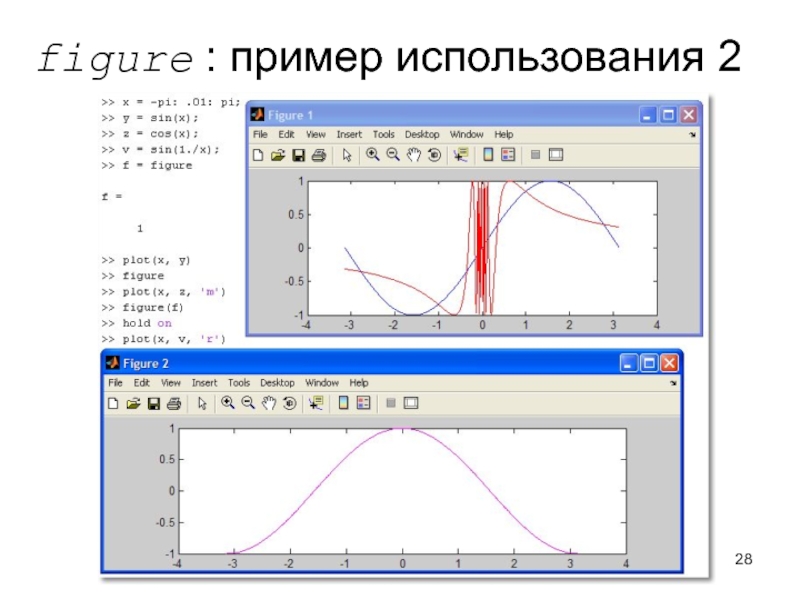
Слайд 26Построение графиков в разных графических окнах
Создать новое графическое окно можно
командой figure
Команда figure создаёт графическое окно и возвращает указатель на
него:
h = figure
Активизировать ранее созданное окно можно командой figure(h)
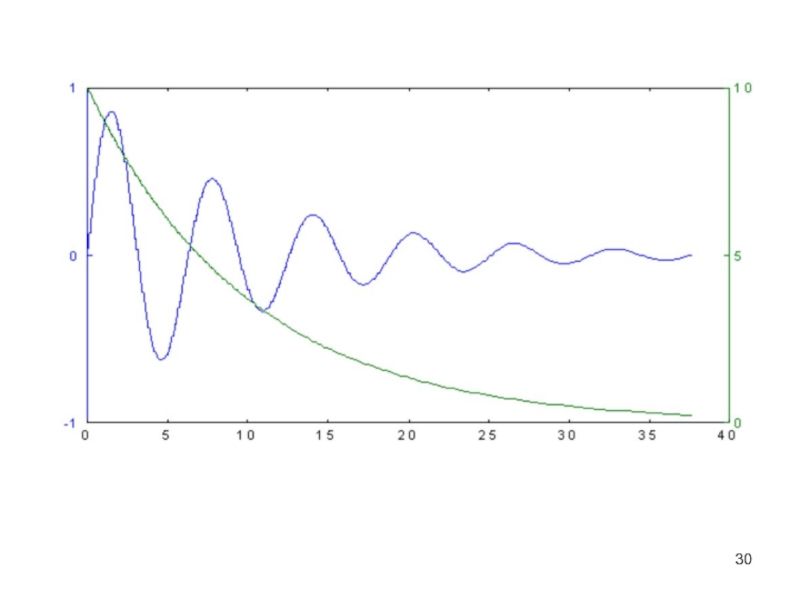
Слайд 29График с двумя осями координат
Одна ось координат отображается слева, другая
справа.
График реализуется функцией
plotyy(x1,y1,x2,y2).
>> x=0:0.01:12*pi;
>> plotyy(x,sin(x).*exp(-0.1.*x),x, 10*exp(-0.1.*x))
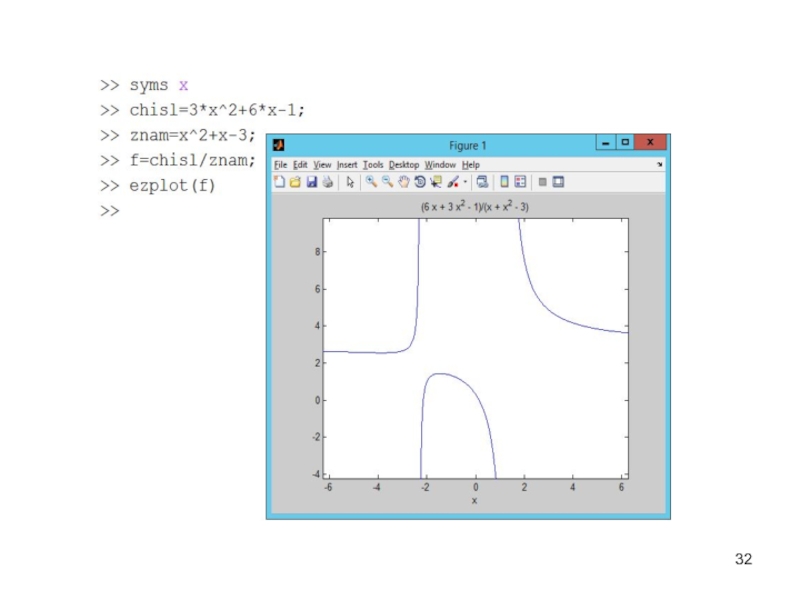
Слайд 31Построение графиков, заданных символьным выражением
Слайд 33Пример 2.
>> ezplot('u^2+v^2-1', [-1,1], [-1,1])
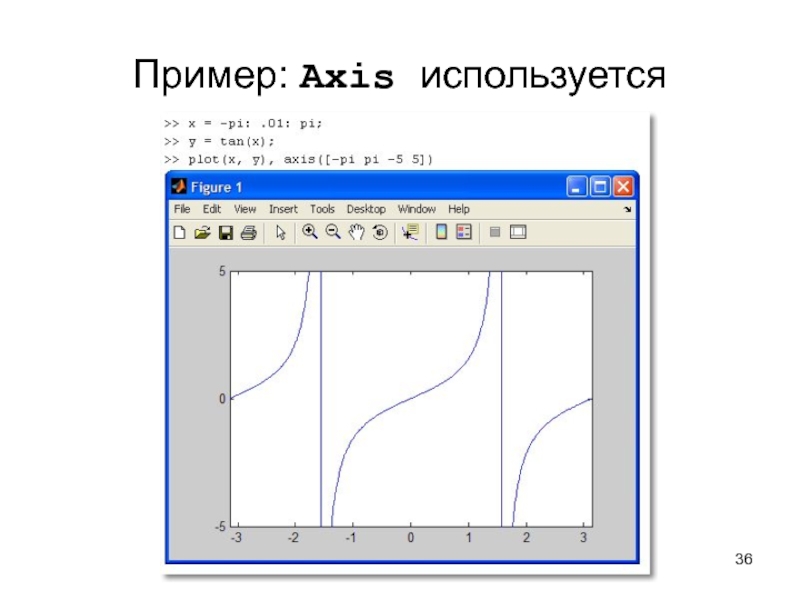
Слайд 34Axis: управление масштабом
Команда
axis([Xmin Xmax Ymin Ymax]) задаёт область построения
графиков по осям X и Y.
Используется, если результат автомасштабирования неудовлетворителен.
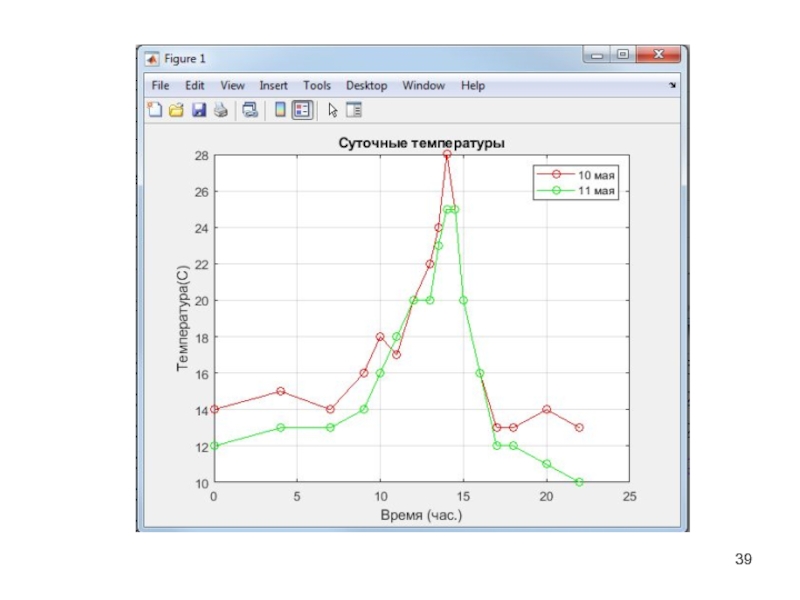
Слайд 37Оформление графиков
Для графиков можно задать
масштабную сетку: grid on
заголовок: title(’заголовок’)
подписи осей:
xlabel(’текст’) и
ylabel(’текст’)
- легенда: legend(’текст’)
В заголовках и подписях можно использовать нотацию системы TeX.
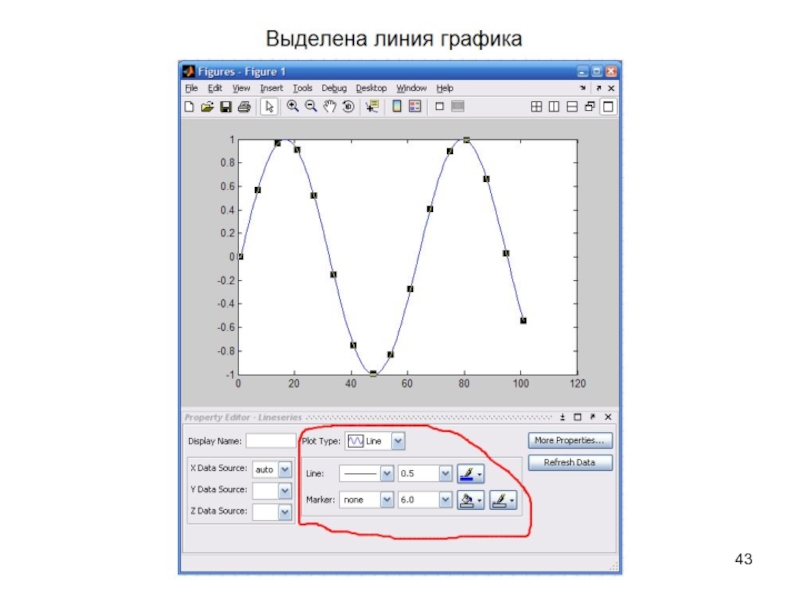
Слайд 41Форматирование графиков
Доступно из меню Edit:
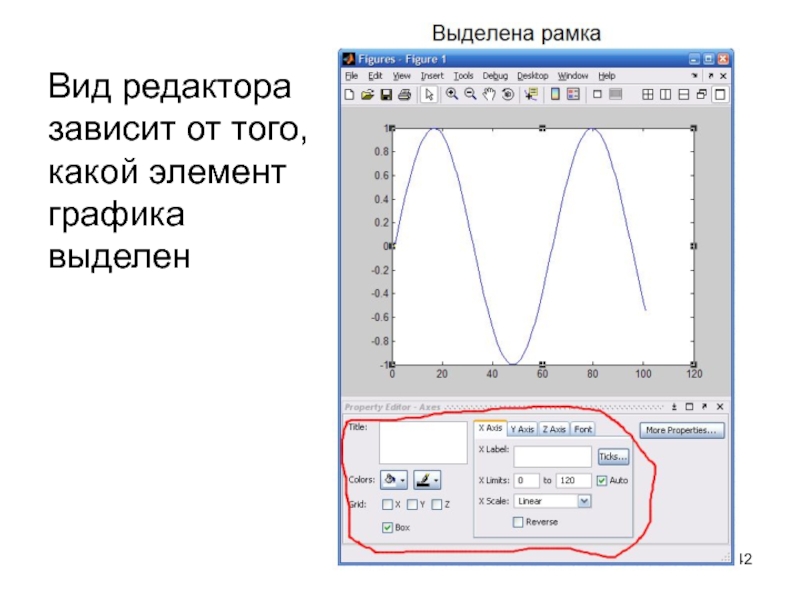
Слайд 42Вид редактора зависит от того, какой элемент графика выделен
Слайд 44Графики функций, заданных параметрически
Строятся при помощи оператора plot.
Вначале задаётся диапазон
построения t.
Затем вычисляются x(t) и y(t).
И строится график.
Слайд 45Графики функций, заданных параметрически
Слайд 46Графики функций, заданных параметрически
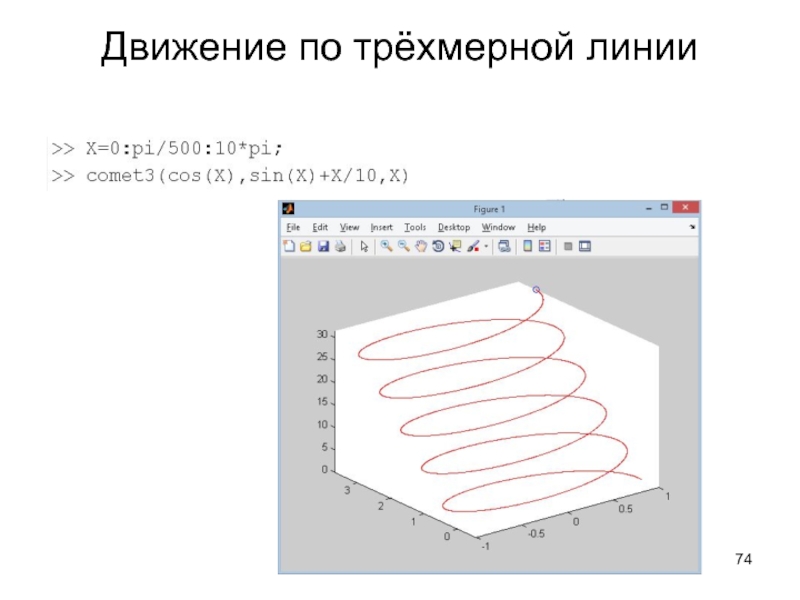
Графики параметрических функций часто возникают в физических
приложениях.
Независимая переменная t в этом случае имеет смысл времени, x
и y – координаты.
Для построения динамического графика можно использовать функцию comet(x,y).
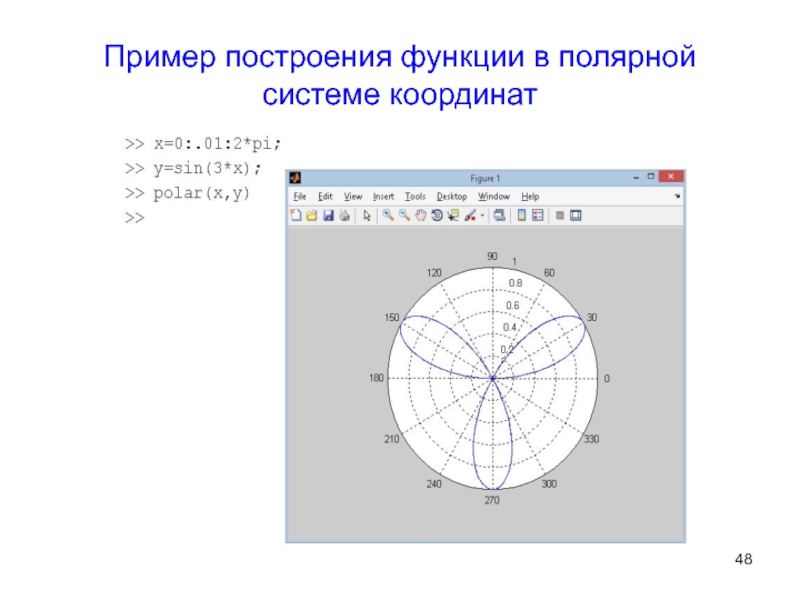
Слайд 47Функции в полярной системе координат
Строятся аналогично графикам функций в декартовой
системе
Для построения используется команда polar.
Слайд 48Пример построения функции в полярной системе координат
Слайд 49Построение диаграмм
Столбиковая диаграмма с вертикальным расположением
Строится при помощи
команд:
bar(x,y) – строит столбиковый график элементов
вектора y при заданных значениях вектора х, которые должны идти в монотонно возрастающем порядке.
Слайд 51 bar(y) – строит график элементов матрицы y
так же, как указано выше, но для построения графика используется
вектор х=1:m.
Возможно применение этих команд со спецификацией
bar(…,’спецификация’),
где ‘спецификация’ – тип линии, цвет и т.д. по аналогии с командой plot.
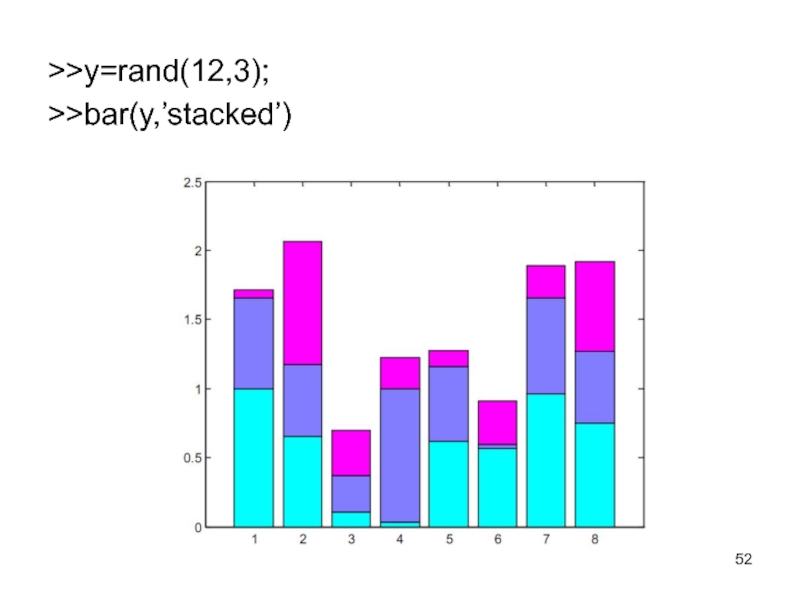
Спецификация ‘stacked’ задает рисование всех n столбцов в позиции m друг на друге.
Слайд 52>>y=rand(12,3);
>>bar(y,’stacked’)
Слайд 53Столбиковая диаграмма с горизонтальным расположением
Строится командой barh(…), аналогичной по синтаксису команде bar(…).
Слайд 54>>y=rand(5,3);
>>barh(y,’stacked’)
Слайд 55Круговая диаграмма
Диаграммы состоят из плоских секторов (аналогичных кусков
пирога) и строятся с помощью функции pie(…).
В
простейшем случае вектор у, содержащий k положительных компонентов генерирует k секторов, центральный угол которых пропорционален вкладу каждого компонента в общую сумму.
Слайд 57Круговая диаграмма c отдельными секторами
Создание выделяющихся элементов обеспечивается
заданием еще одного аргумента такой же размерности, что и вектор
у.
Выдвигаемым секторам в новом векторе должны соответствовать ненулевые элементы.
Слайд 59Построение гистограмм
Классическая гистограмма характеризует число попаданий значений вектора
у в m интервалов.
Для получения данных для гистограмм служит
функция hist, записываемая в следующем виде:
hist(y) - возвращает вектор числа попаданий для 10 интервалов, выбираемых автоматически.
Если у – матрица, то выдается массив данных о числе попаданий для каждого из столбцов.
Слайд 60hist(y,m) – аналогична вышерассмотренной, но используется m интервалов (m-скаляр).
hist(y,х) –
возвращает числа попаданий элементов вектора у в интервалы, центры которых
заданы элементами вектора х.
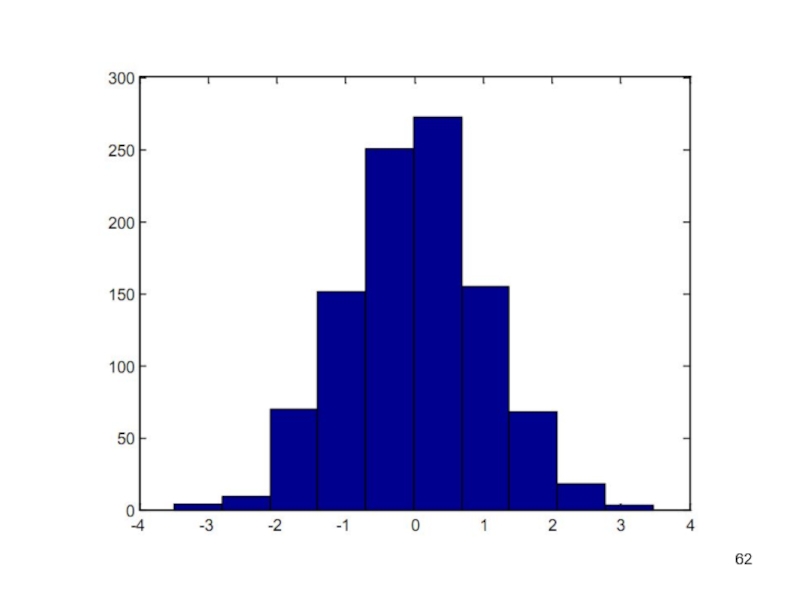
Слайд 61Примеры.
Построить гистограмму для 1000 случайных чисел и вывести вектор с
данными о числах их попаданий для 10 интервалов.
>>y=randn(1000,1);
>>hist(y)
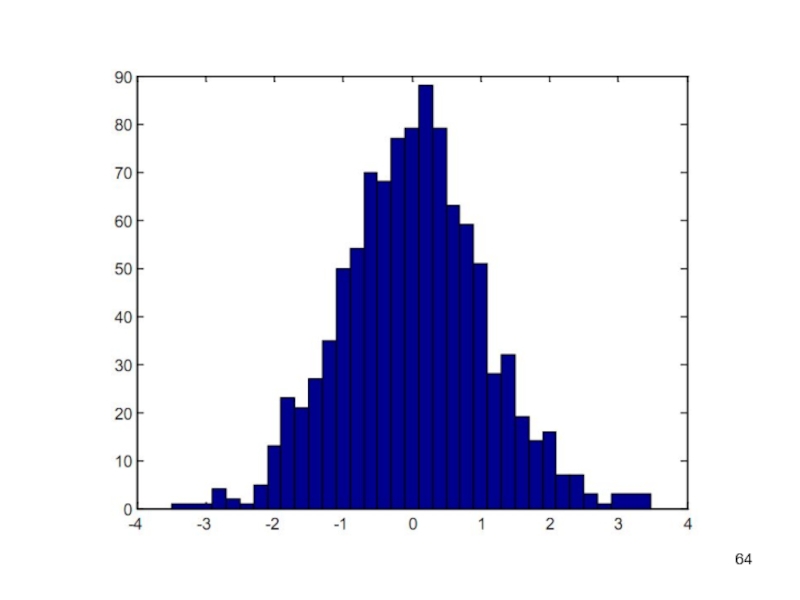
Слайд 63Построить гистограмму для элементов массива у предыдущего примера и интервалов,
центры которых заданы элементами вектора х.
>>x= -3,0.2,3;
>>y=randn(1000,1);
>>hist(y,x)
Слайд 65Построение
поверхностей
контурных диаграмм (линии равного уровня)
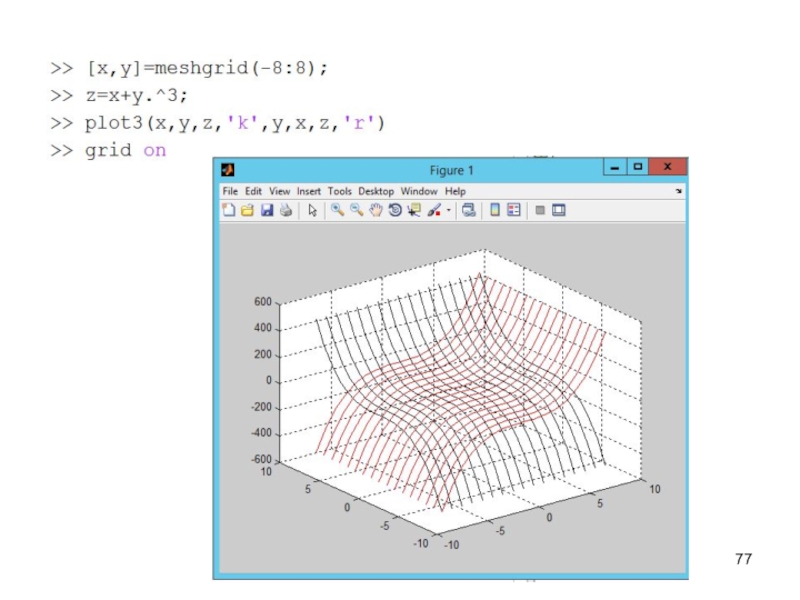
3D-линий
векторных полей
скалярных полей
и др.
Трёхмерная
(3D-) графика
Слайд 68Построение 3D-поверхности
Рассмотрим пример: построить поверхность
f(x,y)=sin(r)/r,
где
r=sqrt(x2+y2)
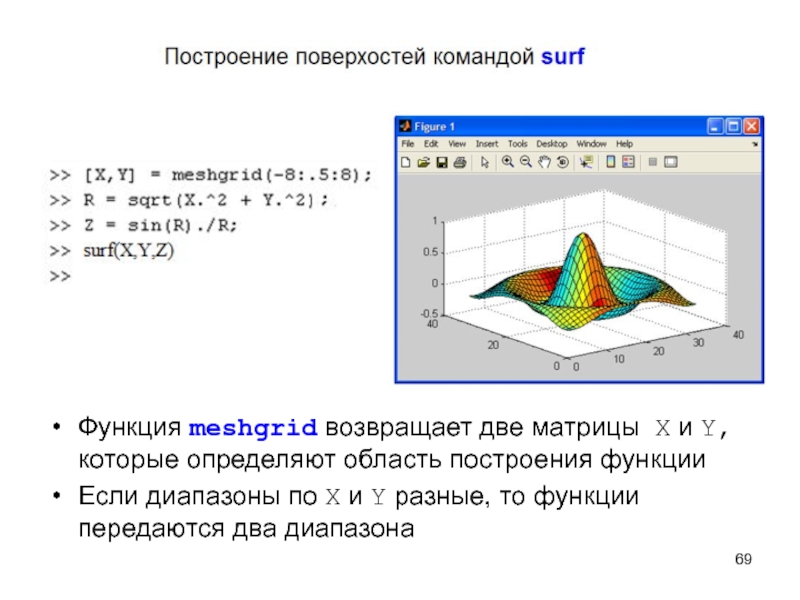
Слайд 69Функция meshgrid возвращает две матрицы X и Y, которые определяют
область построения функции
Если диапазоны по X и Y разные, то
функции передаются два диапазона
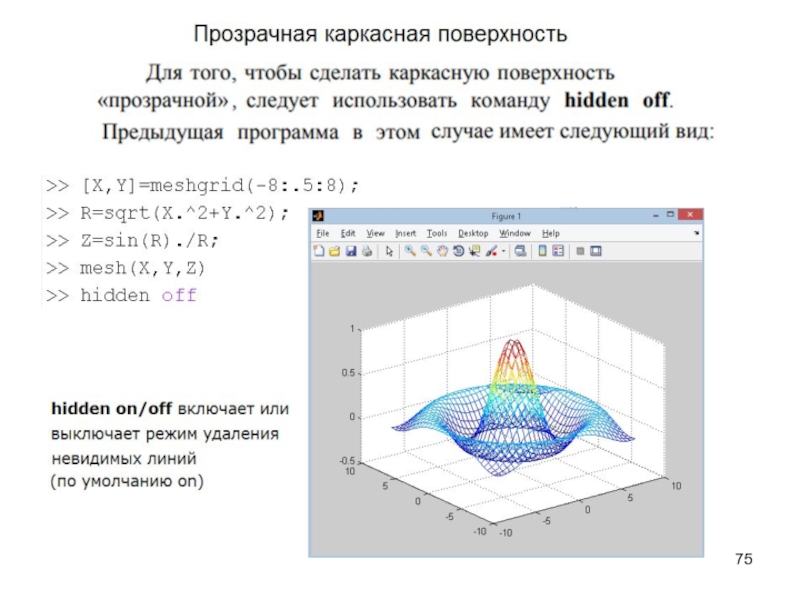
Слайд 70Построение поверхностей командой mesh
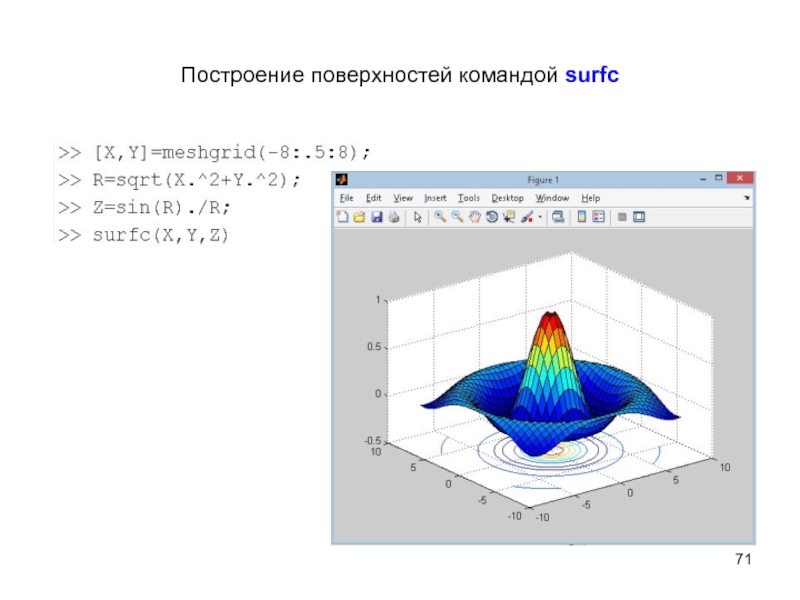
Слайд 71Построение поверхностей командой surfc
Слайд 72Поверхность и контурная диаграмма под ней
Слайд 78Матричная круговая диаграмма
>> y=[5 25 7 10];
>> v=[0,1,0,0];
>> pie3(y,v)
Слайд 79Матричный образ поверхностей
MATLAB имеет несколько графических функций, возвращающих
матричный образ поверхностей. Например, функция peaks(n) возвращает матричный образ поверхности
с рядом пиков и впадин. Такие функции удобно использовать для проверки работы графических команд трехмерной графики.
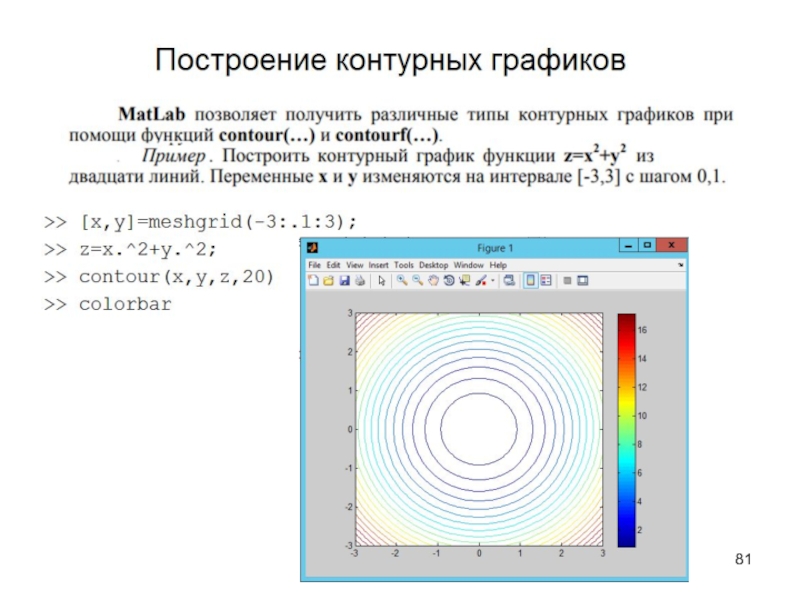
Слайд 82Команда clabel(c, h) маркирует
линии уровня контура, которые
заданы в
векторе h.
![Пример 2. >> ezplot('u^2+v^2-1', [-1,1], [-1,1])](/img/thumbs/4dfe8dddbce3ffe3bf4c9666cfad9f6e-800x.jpg "Графические возможности Matlab Пример 2. >> ezplot('u^2+v^2-1', [-1,1], [-1,1])")
![Axis: управление масштабомКоманда axis([Xmin Xmax Ymin Ymax]) задаёт область построения графиков по осям X и Y.Используется,](/img/thumbs/37d3bb3936543ffeb38f235e426b564f-800x.jpg "Графические возможности Matlab Axis: управление масштабомКоманда axis([Xmin Xmax Ymin Ymax]) задаёт область построения графиков")
![Матричная круговая диаграмма>> y=[5 25 7 10];>> v=[0,1,0,0];>> pie3(y,v)](/img/thumbs/37fd4ed291f939ea29f106b364a900df-800x.jpg "Графические возможности Matlab Матричная круговая диаграмма>> y=[5 25 7 10];>> v=[0,1,0,0];>> pie3(y,v)")
