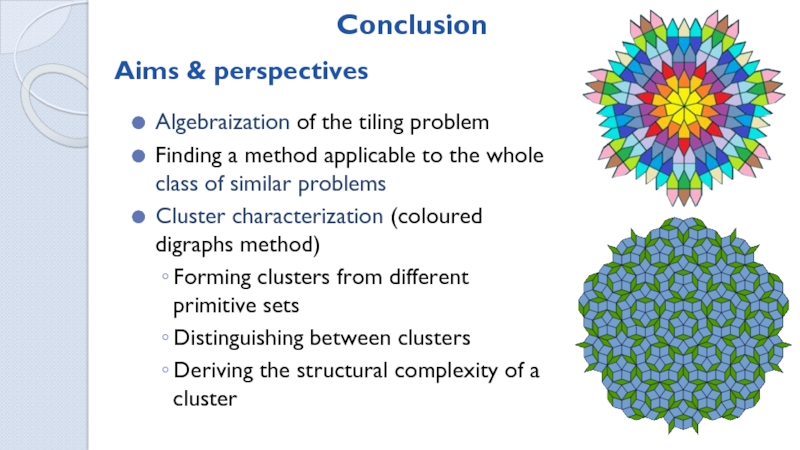
planar graph G
Pfaffian method
Pfaffian orientation
Let A denote the signed
adjacency matrix of G. This means that
• Aij = 0 if no edge joins vi to vj .
• Aij = 1 if the edge joining vi to vj is oriented from vi to vj .
• Aij = −1 if the edge joining vi to vj is oriented from vj to vi .
A perfect matching of G is a collection of edges e1, ..., en of G such that every vertex belongs to exactly one ej .
Let P(G) denote the number of distinct perfect matchings of G. Then
The matrix A is called skew-symmetric if Aij = −Aji for all i, j. A is skew-symmetric.
Let A be a 2n × 2n skew-symmetric matrix. The Pfaffian of A is defined as the sum taken over all permutations of the set {1, ..., 2n}.
Given Muir’s Identity, Kastelyn’s Theorem can be reformulated as follows.
Let G be a graph equipped with any Pfaffian orientation. Let A be the corresponding signed adjacency matrix. Then
Muir’s Identity
1
1 Kastelyn’s Formula for Perfect Matchings. Rich Schwartz
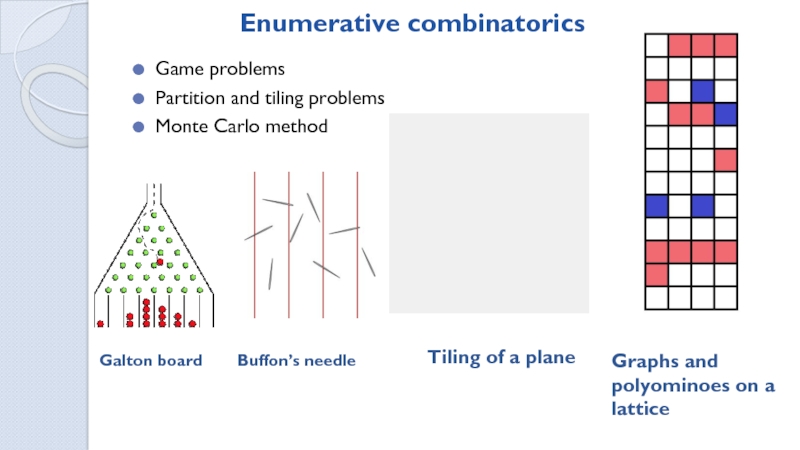
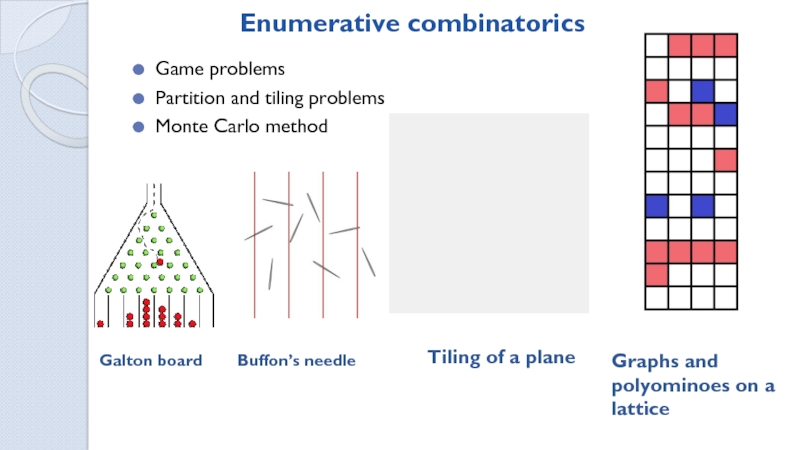
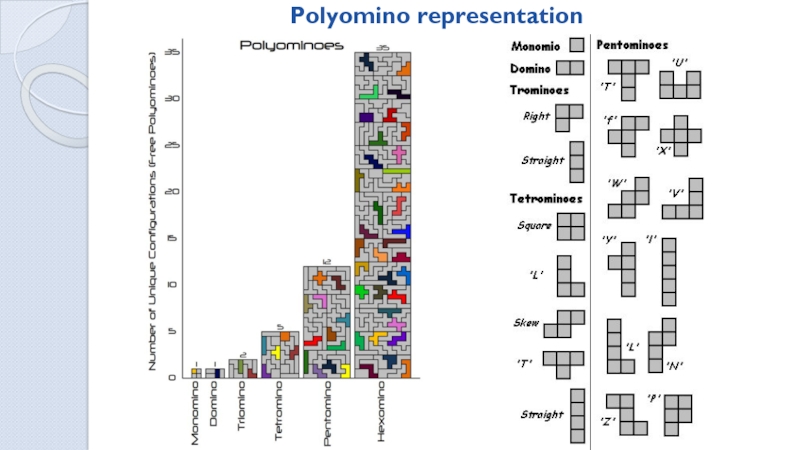
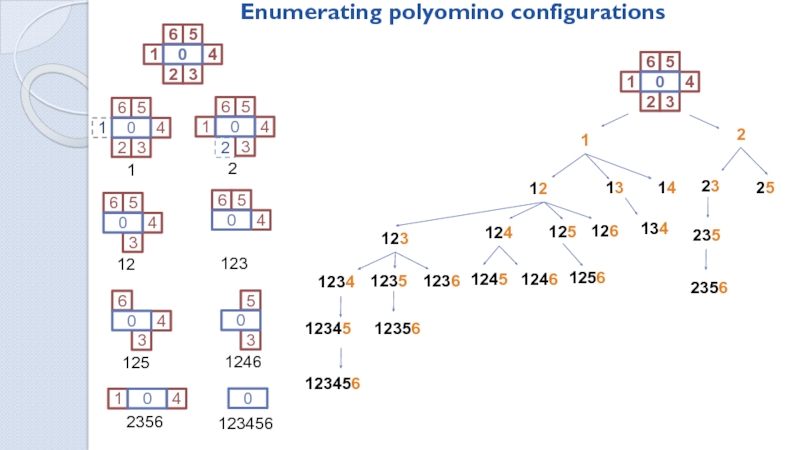
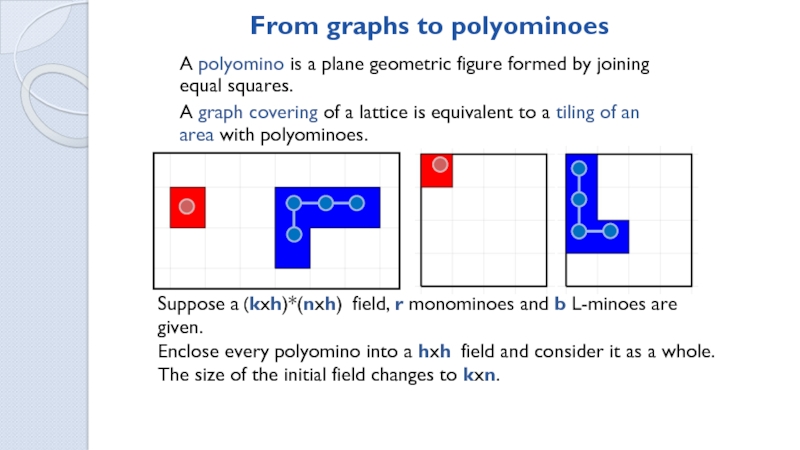
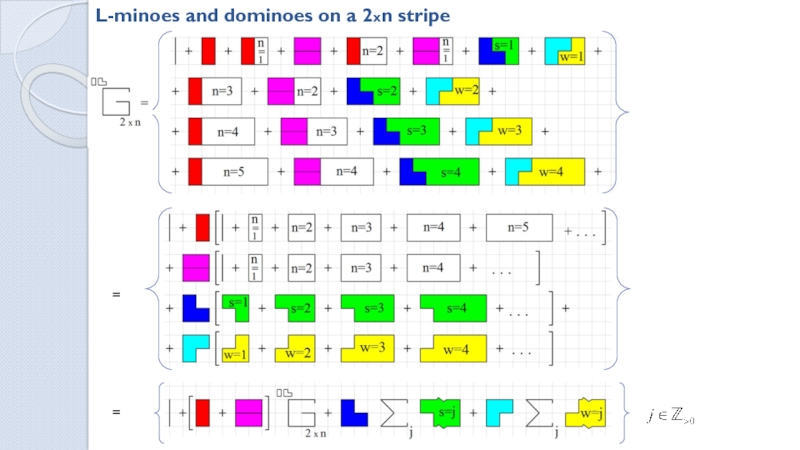
Ways to tile a MxN field with dominoes

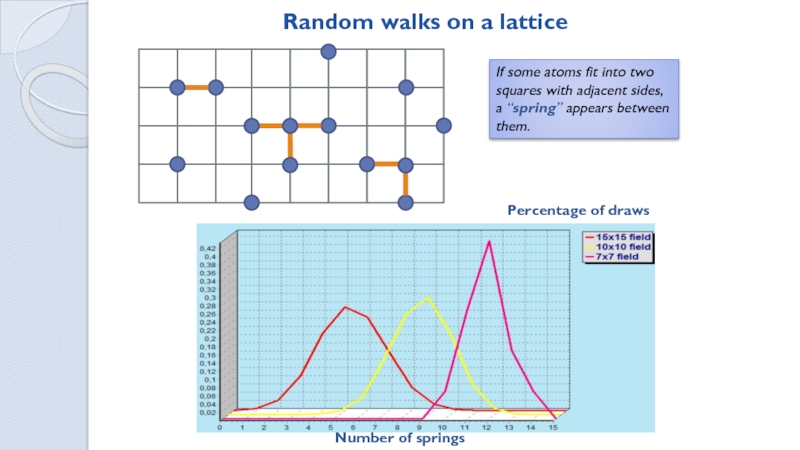


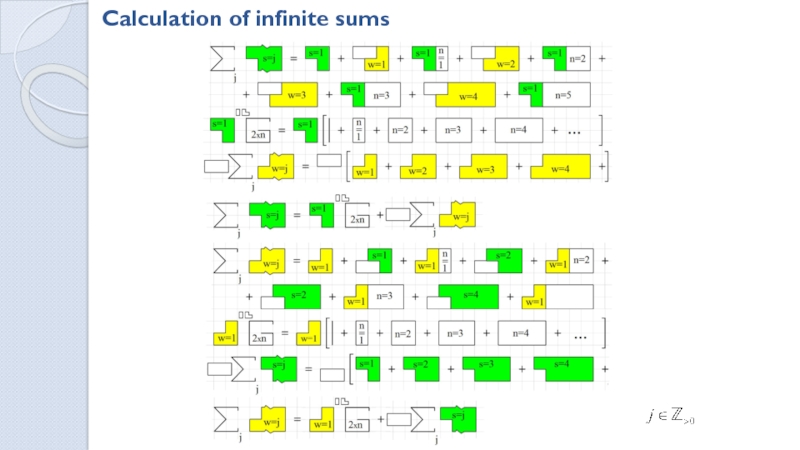
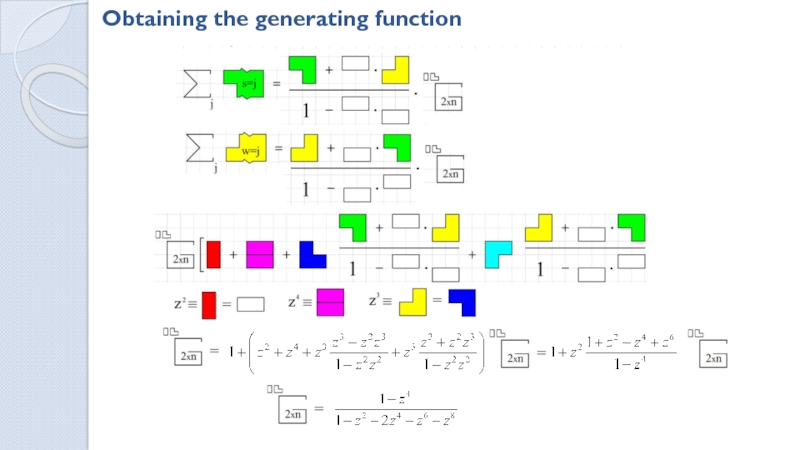
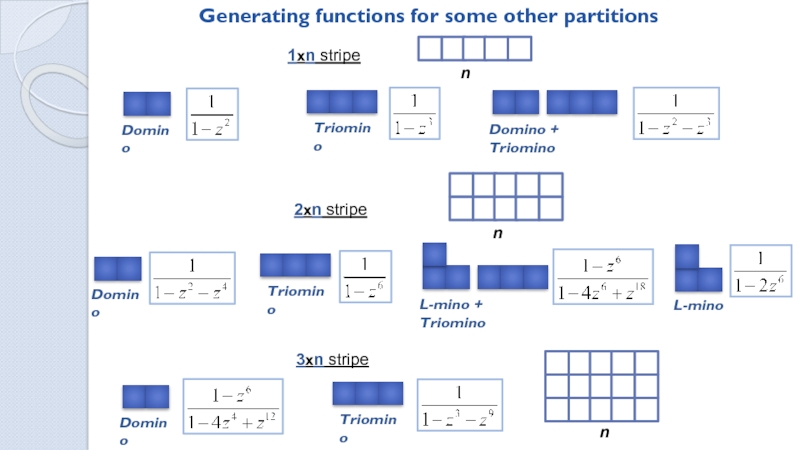
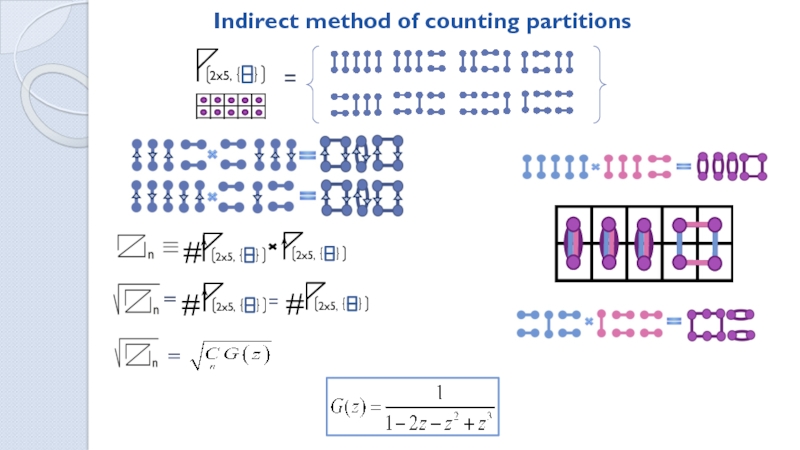
![How many ways are there to tile a rectangle with polyominoes? . . .n-1n. . .n-2nj. . .n-jj. . .n-jnn. . .n221,1[ . . .n-1n. . .n-2nj. . .n-jj. . .n-jnn. . .n221,1[ n=0 ][n=0]1Derivation of the generating function](/img/thumbs/3ca13131894753034f21a9002e6c06c7-800x.jpg)