Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
И НФОРМАЦИЯ U:\phys\ Для ФЗО \А СОИ571
Содержание
- 1. И НФОРМАЦИЯ U:\phys\ Для ФЗО \А СОИ571
- 2. Контрольная работа №1, ЧАСТЬ 2"Механические колебания" Вариант 999
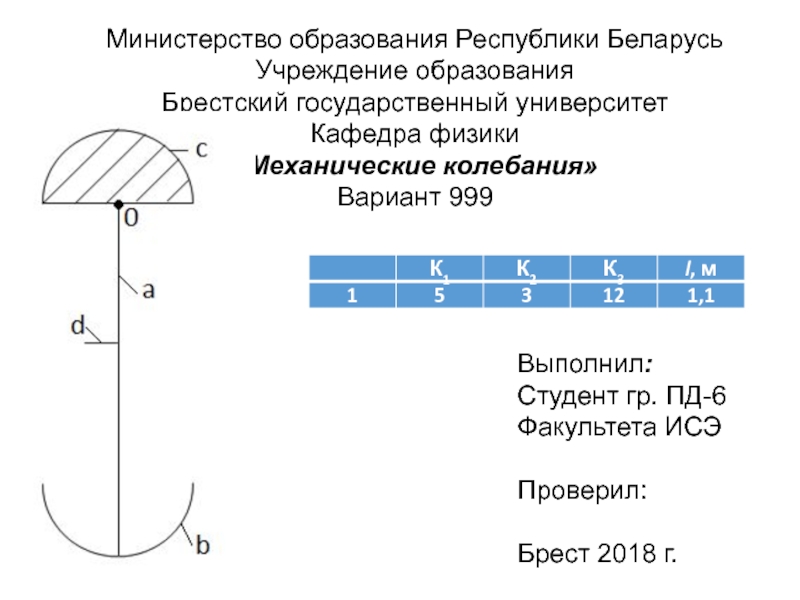
- 3. Министерство образования Республики БеларусьУчреждение образованияБрестский государственный университетКафедра физики«Механические колебания»Вариант 999Выполнил:Студент гр. ПД-6Факультета ИСЭПроверил:Брест 2018 г.
- 4. Механические колебанияФизический маятник на рисунках 2.0-2.9 состоит
- 5. С помощью тонкой нити, привязанной к концу
- 6. 3. Найти угол между тем же стержнем
- 7. 8. С помощью уравнения колебаний найти кинетическую
- 8. Решение. Определим косвенно заданные величины: Масса четвертого
- 9.
- 10.
- 11. Для вычисления ЦМ полукольца возьмем локальную систему
- 12.
- 13. Для нахождения положения центра масс полукольца с
- 14.
- 15.
- 16.
- 17.
- 18. Определим угол между вертикалью (осью Y) и
- 19. Скачать презентанцию
Контрольная работа №1, ЧАСТЬ 2"Механические колебания" Вариант 999
Слайды и текст этой презентации
Слайд 3Министерство образования Республики Беларусь
Учреждение образования
Брестский государственный университет
Кафедра физики
«Механические колебания»
Вариант 999
Выполнил:
Студент
гр. ПД-6
Слайд 4Механические колебания
Физический маятник на рисунках 2.0-2.9 состоит из четырех элементов:
1) – тонкого стержня длиной l; 2) – сделанной из
такого же по толщине и из такого же материала стержня полуокружности с диаметром или без него; 3) плоской пластинки в виде полукруга радиусом l/K1 ; 4) тонкого стержня из того же материала и той же толщины, но с длиной l/K2. Массы первых трех элементов одинаковы. Место прикрепления короткого стержня задайте самостоятельно. Система может колебаться вокруг горизонтальной оси О, показанной на рисунке.
Слайд 5С помощью тонкой нити, привязанной к концу короткого стержня, систему
можно тянуть под углом α к горизонту влево или вправо
в зависимости от расположения стержня на рисунке с силой mg/K3, где m=2 кг общая масса системы.Выполнить следующие задания:
1. Определить расстояние от оси подвеса до центра масс системы.
2. Найти угол между стержнем длиной l и вертикалью, если система находится в положении равновесия в отсутствие нити, к которой приложена сила, равная mg/K2.
Слайд 63. Найти угол между тем же стержнем и вертикалью при
наличии указанной силы.
4. Считая угол отклонения системы от положения равновесия
малым, найти потенциальную энергию системы в отклоненном от равновесия положении.5. Найти момент инерции системы относительно оси подвеса.
6. При t=0 нить пережигают, и система начинает совершать колебания. Считая их малыми, написать уравнение колебаний. Найти период и частоту колебаний.
7. Найти приведенную длину физического маятника.
Слайд 78. С помощью уравнения колебаний найти кинетическую энергию системы в
момент прохождения равновесия и используя результат п. 4 убедиться в
выполнении закона сохранения механической энергии.9. В некоторый момент времени, задаваемый самостоятельно, короткий стержень без толчка отделяется от системы. Написать уравнение новых колебаний, сохранив первоначальное начало отсчета времени.
Слайд 8Решение.
Определим косвенно заданные величины: Масса четвертого стержня m4=m1/K2=m1/2. Массы
элементов определятся из равенства:
m1+m2+m3+m4=2 кг. 3.5 m1=2 кг, откуда
m1=m2=m3=0.571
кг. (1)m4=0.2857 кг. (2)
Радиус второго элемента найдется из условия идентичности его материала материалу стержня l1 и равенства их масс. Следовательно, длина второго элемента, состоящего из полуокружности и диаметра равна длине l1. πR2+2R=l1, откуда
R2=l1/(π+2) = 0.194 м. (3)
Слайд 11Для вычисления ЦМ полукольца возьмем локальную систему координат с осью
Х, не имеющую отношения к системе координат, выбранной для решения
всей задачи.
Слайд 13Для нахождения положения центра масс полукольца с диаметральным стержнем необходимы
их массы. Нам же известна только общая их масса m2=m21+m22.
Конечно вычислить m21и m22 очень просто, поскольку они сделаны из одинакового материала. Поэтому их массы относятся как их длины: m21/m22=π/2. Используя это найдем:m21=m2π/(2+π)=0.349 кг, (1.5)
m22=2m2/(2+π)=0.222 кг. (1.6)
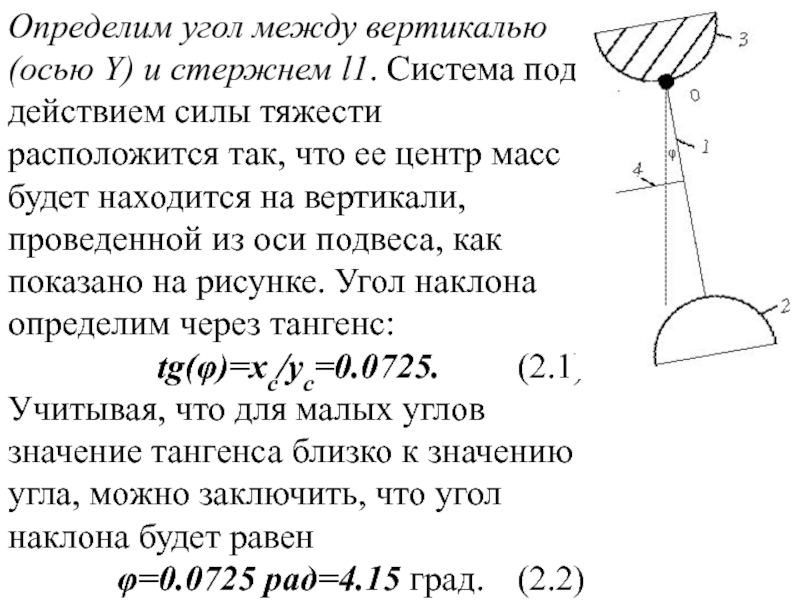
Слайд 18Определим угол между вертикалью (осью Y) и стержнем l1. Система
под действием силы тяжести расположится так, что ее центр масс
будет находится на вертикали, проведенной из оси подвеса, как показано на рисунке. Угол наклона определим через тангенс:tg(φ)=хс/ус=0.0725. (2.1)
Учитывая, что для малых углов значение тангенса близко к значению угла, можно заключить, что угол наклона будет равен
φ=0.0725 рад=4.15 град. (2.2)