Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Импульс. Закон сохранения импульса
Содержание
- 1. Импульс. Закон сохранения импульса
- 2. О неизменности в мире …«Я принимаю, что
- 3. Импульс. Закон сохранения импульса.Импульс тела. Импульс силы.Закон сохранения импульса.Применение закона сохранения импульса – реактивное движение.
- 4. Объясните явления…
- 5. Второй закон НьютонаF=maa = v- v 0
- 6. Импульс силы – мера механического взаимодействия, характеризующая
- 7. Проинтегрируем на данном промежутке времени:Количество движения точки
- 8. По определению центра масс:Тогда:Вектор количества движения системы
- 9. Просуммируем эти уравненияпо всем точкам:В левой части
- 10. Следствия из теоремы об изменении количества движения
- 11. Пример: Граната массы M, летевшая со скоростью
- 12. Разделяем переменные и интегрируем :Правый интеграл практически равен нулю, т.к. время взрыва t
- 13. 2. Отбрасываем связи и заменяем их действие
- 14. Принимая произведение плотности, площади поперечного сечения и
- 15. Второй закон Ньютона в импульсной форме:Импульс силы
- 16. Если два или несколько тел взаимодействуют только
- 17. Закон сохранения им пульса:Векторная сумма импульсов замкнутой системы тел не изменяется.
- 18. Слайд 18
- 19. Абсолютно упругий удар — модель соударения, при
- 20. Для математического описания простейших абсолютно упругих ударов,
- 21. Центральный абсолютно упругий удар Когда оба
- 22. После нецентрального упругого соударения шары разлетаются под
- 23. Слайд 23
- 24. Абсолютно неупругий удар — удар, в
- 25. Реактивное движение
- 26. Реактивное движение, например, выполняет ракета. Продукты сгорания
- 27. ЗАДАЧА:
- 28. Реактивное движение в живой природе:Реактивное движение присуще медузам, кальмарам, осьминогам и другим живым организмам.
- 29. Реактивное движение можно обнаружить и в мире
- 30. В технике реактивно движение встречается на речном транспорте (катер с водометным двигателем), в авиации, космонавтике,военном деле.
- 31. Легкий шар движущийся со скоростью 10 м/с,
- 32. Брусок массой 600 г, движущийся со
- 33. Два шарика массы которых
- 34. Шарик массой 100 г, летящий
- 35. Скачать презентанцию
Слайды и текст этой презентации
Слайд 2О неизменности в мире …
«Я принимаю, что во Вселенной …
есть известное количество движения,
которое никогда не увеличивается,
не уменьшается,
таким образом, если одно тело приводит в движение
другое, то теряет столько своего
движения, сколько его сообщает».
В XVII веке впервые были указаны величины, сохраняющиеся в тех или иных явлениях.
Слайд 3Импульс. Закон сохранения импульса.
Импульс тела. Импульс силы.
Закон сохранения импульса.
Применение закона
сохранения импульса – реактивное движение.
Слайд 5Второй закон Ньютона
F=ma
a = v- v 0 / t
Ft =
mv - mv0
p = mv - импульс тела
p =
кг м/с СИFt - импульс силы.
mv - mv0 – изменение им пульса
тела
Слайд 6Импульс силы – мера механического взаимодействия, характеризующая передачу механического движения
со стороны действующих на точку сил за данный промежуток времени:
В
проекцияхна координатные оси:
В случае постоянной силы:
В проекциях на координатные оси:
Импульс равнодействующей – равен геометрической сумме импульсов приложенных к точке сил за один и тот же промежуток времени:
Умножим на dt:
Слайд 7Проинтегрируем на данном промежутке времени:
Количество движения точки – мера механического
движения, определяемая вектором, равным произведению массы точки на вектор ее
скорости:Количество движения системы материальных точек – геометрическая сумма количеств движения материальных точек:
Слайд 8По определению центра масс:
Тогда:
Вектор количества движения системы равен произведению массы
всей системы на вектор скорости центра масс системы.
В проекциях на
координатные оси:
Теорема об изменении количества движения системы – Рассмотрим систему n материальных точек. Приложенные к каждой точке силы разделим на внешние и внутренние и заменим их на соответствующие равнодействующие Fke и Fki. Запишем для каждой точки основное уравнение динамики: или
Слайд 9Просуммируем эти уравнения
по всем точкам:
В левой части уравнения внесем массы
под знак производной и заменим сумму производных на производную суммы:
Из
определения количества движения системы:Производная вектора количества движения системы
по времени равна главному вектору внешних
сил системы.
В проекциях
на координатные оси:
Слайд 10Следствия из теоремы об изменении количества движения системы
(законы сохранения):
1. Если
в интервале времени [t1, t2] главный вектор внешних сил системы
равен
нулю, Re = 0, то вектор количества движения постоянен, Q = const– закон сохранения количества движения системы).
2. Если в интервале времени [t1, t2] проекция главного вектора внешних сил
системы на ось x равна нулю, Rxe = 0, то проекция количества движения
системы на ось x постоянна, Qx = const.
Аналогичные утверждения справедливы для осей y и z.
Слайд 11Пример: Граната массы M, летевшая со скоростью v, разорвалась на
две части. Скорость одного из осколков массы m1 возросла в
направлении движения до величины v1. Определить скорость второго осколка.1. Объект движения (граната):
2. Объект – свободная система, связи и их реакции отсутствуют.
3. Добавляем активные силы:
4. Записываем теорему об изменении количества движения:
Проецируем на ось :
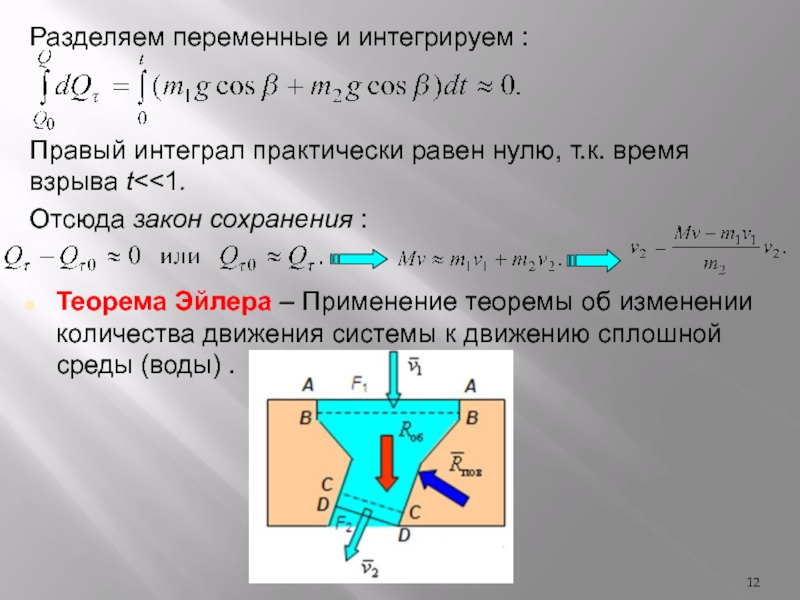
Слайд 12Разделяем переменные и интегрируем :
Правый интеграл практически равен нулю, т.к.
время взрыва t
об изменении количества движения системы к движению сплошной среды (воды) .Слайд 132. Отбрасываем связи и заменяем их действие реакциями
(Rпов –
равнодействующая поверхностных сил)
1.Выбираем в качестве объекта движения
объем воды,
находящийся в криволинейном канале турбины: 3. Добавляем активные силы
(Rоб – равнодействующая объемных сил):
4. Записываем теорему об изменении
количества движения системы:
Изменение количества движения воды в интервале времени [t0,t1] :
Изменение количества движения воды
за бесконечно малый интервал времени dt: , где
Слайд 14Принимая произведение плотности, площади
поперечного сечения и скорости за секундную
массу
получаем:
Подставляя дифференциал количества движения системы
в теорему об изменении получаем:
В проекциях
на оси:Разность проекций векторов секундных количеств движения жидкости на ось равна сумме проекций главных векторов объемных и поверхностных сил на ту же ось.
Слайд 15Второй закон Ньютона в импульсной форме:
Импульс силы равен
изменению импульса
тела.
Импульс - векторная величина. Он всегда совпадает по направлению
с вектором скорости.Слайд 16Если два или несколько тел взаимодействуют только между собой
( не подвергаются воздействию внешних сил),
то эти тела образуют замкнутую систему.Импульс каждого из тел, входящих в замкнутую систему может меняться в результате их взаимодействия друг с другом.
Для описания существует очень важный закон – закон сохранения импульса.
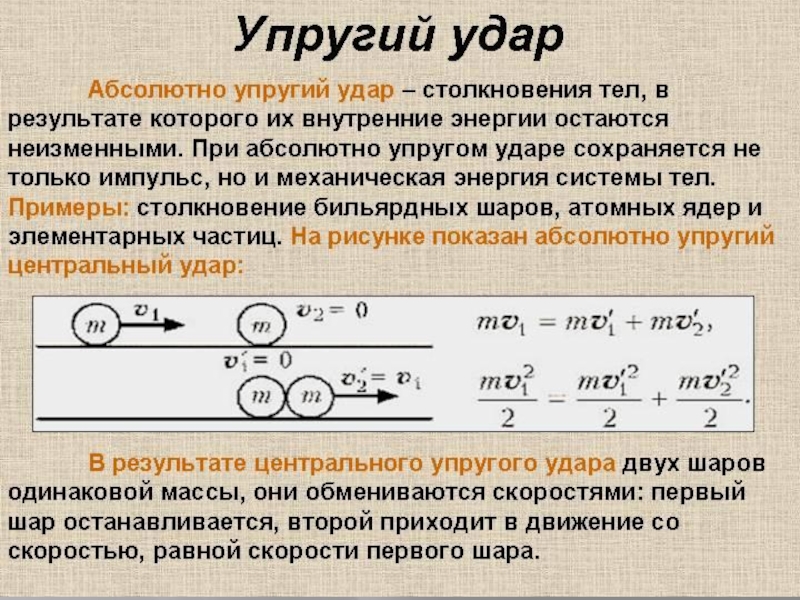
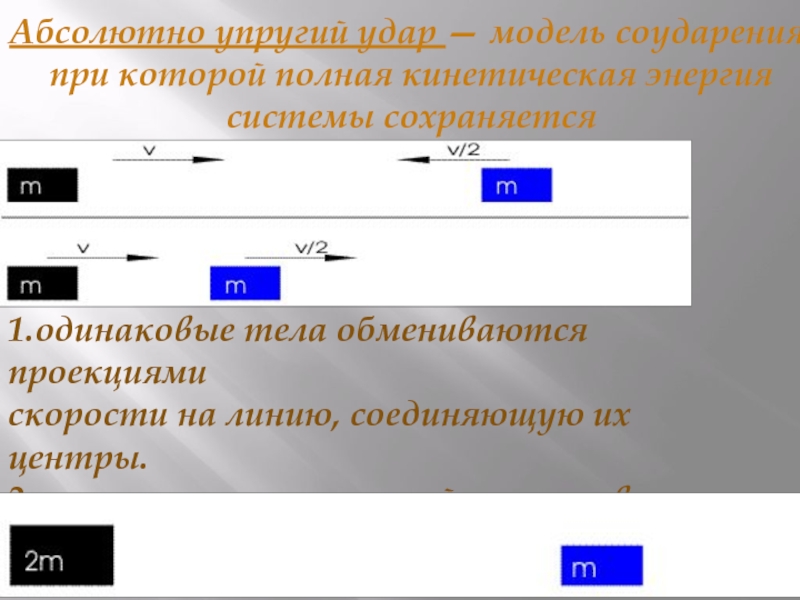
Слайд 19Абсолютно упругий удар — модель соударения, при которой полная кинетическая
энергия системы сохраняется
1.одинаковые тела обмениваются проекциями
скорости на линию, соединяющую их
центры.2. скорости тел различной массы зависят от соотношения масс тел.
Слайд 20Для математического описания простейших абсолютно упругих ударов, используется:
закон сохранения импульса
закон
сохранения энергии
абсолютно упругий удар тел не равных масс
Импульсы складываются векторно, а энергии скалярно!
абсолютно упругий удар
тел равных масс
Слайд 21
Центральный абсолютно упругий удар
Когда оба шара имеют одинаковые массы (m1
= m2), первый шар после соударения останавливается (v1 = 0),
а второй движется со скоростью v2 = v1, т. е. шары обмениваются скоростями (импульсами)Центральным ударом шаров называют соударение, при котором скорости шаров до и после удара направлены по линии центров.
Слайд 22После нецентрального упругого соударения шары разлетаются под некоторым углом друг
к другу
Если массы шаров одинаковы, то векторы скоростей шаров после
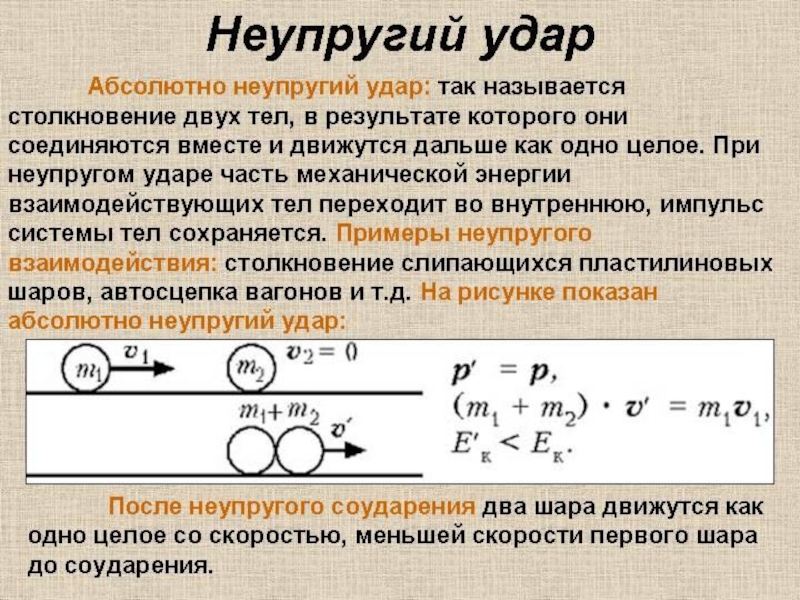
нецентрального упругого соударения всегда направлены перпендикулярно друг к другуСлайд 24 Абсолютно неупругий удар — удар, в результате которого компоненты скоростей
тел становятся равными
При абсолютно неупругом ударе, выполняется закон сохранения импульса,
но не выполняется закон сохранения механической энергии (часть кинетической энергии соударямых тел, в результате неупругих деформаций переходит в тепловую)Слайд 25Реактивное движение
Реактивное движение —
это движение, которое
возникает при отделении
от тела некоторой его
части с определенной
скоростью.
Особенностью этого движения является то, что тело может ускоряться и тормозить без какой-либо внешней взаимодействия с другими телами.
Слайд 26Реактивное движение, например, выполняет ракета.
Продукты сгорания при вылете получают
относительно ракеты некоторую скорость. Согласно закону сохранения импульса, сама ракета
получает такой же импульс, как и газ, но направленый в другую сторону. Закон сохранения импульса нужен для расчета скорости ракеты.Слайд 27 ЗАДАЧА:
До запуска ракеты
Mрυр=0, mгυг=0 После запуска
С какой скоростью будет двигаться ракета, если средняя скорость выхлопных газов 1 км/с, а масса горючего составляет 80% от всей массы ракеты?
мрυр
mгυг
Слайд 28Реактивное движение в живой природе:
Реактивное движение присуще медузам, кальмарам, осьминогам
и другим живым организмам.
Слайд 29Реактивное движение можно обнаружить и в мире растений. В южных
странах и на нашем побережье Черного моря произрастает растение под
названием «бешеный огурец» . При созревании семян внутри плода создаетсявысокое давление в
результате чего плод
отделяется от подложки,
а семена с большой силой
выбрасываются наружу.
Сами огурцы при этом отлетают в противоположном направлении. Стреляет «бешеный огурец» более чем на 12 метров.
Слайд 30В технике реактивно движение встречается на речном
транспорте
(катер с
водометным двигателем),
в авиации, космонавтике,
военном деле.
Слайд 31Легкий шар движущийся со скоростью 10 м/с, налетает на покоящийся
тяжелый шар и между шарами происходит абсолютно упругий удар. После
удара шары разлетаются в противоположные стороны с одинаковыми скоростями. Во сколько раз различаются массы шаровРешение:
Слайд 32 Брусок массой 600 г, движущийся со скоростью 2 м/с,
сталкивается с неподвижным бруском массой 200 г.
Определите
изменение кинетической энергии первого бруска после столкновения. Удар считать
центральным и абсолютно упругим.
Решение:
Слайд 33 Два шарика массы которых соответственно 200 г
и
600 г, висят, соприкасаясь, на одинаковых вертикальных
нитях длиной 80 см. Первый шар отклонили на угол 90° и отпустили. Каким будет отношение кинетических
энергий тяжелого и легкого шариков тотчас
после их абсолютно упругого центрального удара.
Решение:
Слайд 34 Шарик массой 100 г, летящий горизонтально со
скоростью 5 м/с, абсолютно упруго ударяется о
неподвижный шар
массой 400 г, висящий на нитидлиной 40 см. Удар центральный. На какой угол
отклонится шар , подвешенный на нити после удара
Решение:









![Импульс. Закон сохранения импульса Следствия из теоремы об изменении количества движения системы(законы сохранения):1. Если в Следствия из теоремы об изменении количества движения системы(законы сохранения):1. Если в интервале времени [t1, t2] главный вектор](/img/thumbs/be48258b73055eeb8b3cde3f9aea304c-800x.jpg)