Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Интеллектуальные информационные системы
Содержание
- 1. Интеллектуальные информационные системы
- 2. ТЕМА 2. ЗНАНИЯ И ИХ ПРЕДСТАВЛЕНИЕ В
- 3. ТЕМА 2. ЗНАНИЯ И ИХ ПРЕДСТАВЛЕНИЕ В
- 4. Деревья решений – это способ представления правил
- 5. ТЕМА 2. ЗНАНИЯ И ИХ ПРЕДСТАВЛЕНИЕ В
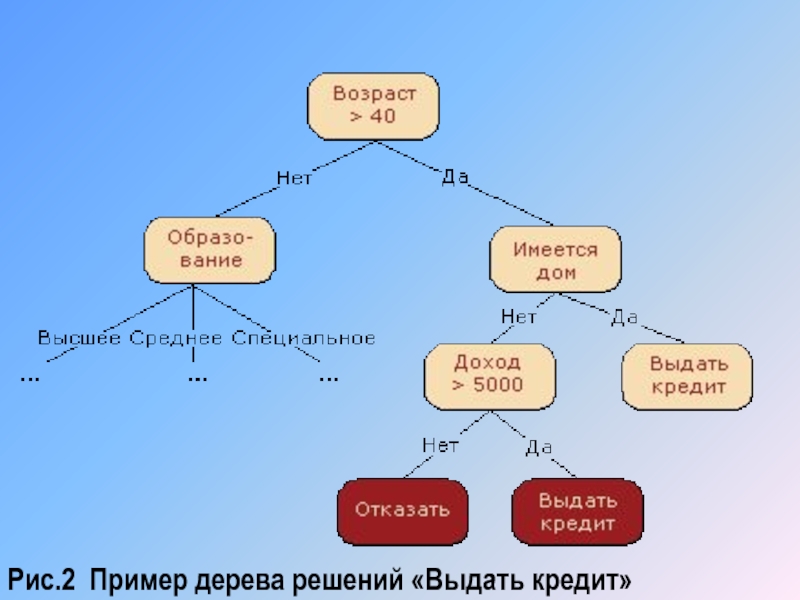
- 6. Рис.2 Пример дерева решений «Выдать кредит»
- 7. ТЕМА 2. ЗНАНИЯ И ИХ ПРЕДСТАВЛЕНИЕ В
- 8. ТЕМА 2. ЗНАНИЯ И ИХ ПРЕДСТАВЛЕНИЕ В
- 9. ТЕМА 2. ЗНАНИЯ И ИХ ПРЕДСТАВЛЕНИЕ В
- 10. ТЕМА 2. ЗНАНИЯ И ИХ ПРЕДСТАВЛЕНИЕ В
- 11. ТЕМА 2. ЗНАНИЯ И ИХ ПРЕДСТАВЛЕНИЕ В
- 12. ТЕМА 2. ЗНАНИЯ И ИХ ПРЕДСТАВЛЕНИЕ В
- 13. ТЕМА 2. ЗНАНИЯ И ИХ ПРЕДСТАВЛЕНИЕ В
- 14. ТЕМА 2. ЗНАНИЯ И ИХ ПРЕДСТАВЛЕНИЕ В
- 15. ТЕМА 2. ЗНАНИЯ И ИХ ПРЕДСТАВЛЕНИЕ В
- 16. ТЕМА 2. ЗНАНИЯ И ИХ ПРЕДСТАВЛЕНИЕ В
- 17. ТЕМА 2. ЗНАНИЯ И ИХ ПРЕДСТАВЛЕНИЕ В
- 18. ТЕМА 2. ЗНАНИЯ И ИХ ПРЕДСТАВЛЕНИЕ В
- 19. ТЕМА 2. ЗНАНИЯ И ИХ ПРЕДСТАВЛЕНИЕ В
- 20. ТЕМА 2. ЗНАНИЯ И ИХ ПРЕДСТАВЛЕНИЕ В
- 21. ТЕМА 2. ЗНАНИЯ И ИХ ПРЕДСТАВЛЕНИЕ В
- 22. ТЕМА 2. ЗНАНИЯ И ИХ ПРЕДСТАВЛЕНИЕ В СИСТЕМАХ ИИ 4 Продукционные моделиРисунок 2.7 Продукционная система21
- 23. ТЕМА 2. ЗНАНИЯ И ИХ ПРЕДСТАВЛЕНИЕ В
- 24. ТЕМА 2. ЗНАНИЯ И ИХ ПРЕДСТАВЛЕНИЕ В
- 25. ТЕМА 2. ЗНАНИЯ И ИХ ПРЕДСТАВЛЕНИЕ В
- 26. ТЕМА 2. ЗНАНИЯ И ИХ ПРЕДСТАВЛЕНИЕ В
- 27. ТЕМА 2. ЗНАНИЯ И ИХ ПРЕДСТАВЛЕНИЕ В
- 28. ТЕМА 2. ЗНАНИЯ И ИХ ПРЕДСТАВЛЕНИЕ В
- 29. ТЕМА 2. ЗНАНИЯ И ИХ ПРЕДСТАВЛЕНИЕ В
- 30. ТЕМА 2. ЗНАНИЯ И ИХ ПРЕДСТАВЛЕНИЕ В
- 31. ТЕМА 2. ЗНАНИЯ И ИХ ПРЕДСТАВЛЕНИЕ В
- 32. ТЕМА 2. ЗНАНИЯ И ИХ ПРЕДСТАВЛЕНИЕ В
- 33. ТЕМА 2. ЗНАНИЯ И ИХ ПРЕДСТАВЛЕНИЕ В
- 34. Скачать презентанцию
Слайды и текст этой презентации
Слайд 1
Интеллектуальные информационные системы
Т.Ф. Лебедева
КАФЕДРА ВЫЧИСЛИТЕЛЬНОЙ ТЕХНИКИ И ИНФОРМАЦИОННЫХ ТЕХНОЛОГИЙ
КемИ РГТЭУ
Слайд 2ТЕМА 2. ЗНАНИЯ И ИХ ПРЕДСТАВЛЕНИЕ В СИСТЕМАХ ИИ
Деревья
решений - общие принципы работы
Стремительное развитие информационных технологий, в частности,
прогресс в методах сбора, хранения и обработки данных позволил многим организациям собирать огромные массивы данных, которые необходимо анализировать. Объемы этих данных настолько велики, что возможностей экспертов уже не хватает, что породило спрос на методы автоматического исследования (анализа) данных, который с каждым годом постоянно увеличивается.Деревья решений – один из таких методов автоматического анализа данных, относящихся к технологиям Data Mining. Первые идеи создания деревьев решений восходят к работам Ховленда (Hoveland) и Ханта(Hunt) конца 50-х годов XX века. Однако, основополагающей работой, давшей импульс для развития этого направления, явилась книга Ханта (Hunt, E.B.), Мэрина (Marin J.) и Стоуна (Stone, P.J) "Experiments in Induction", увидевшая свет в 1966г.
1
Слайд 3ТЕМА 2. ЗНАНИЯ И ИХ ПРЕДСТАВЛЕНИЕ В СИСТЕМАХ ИИ
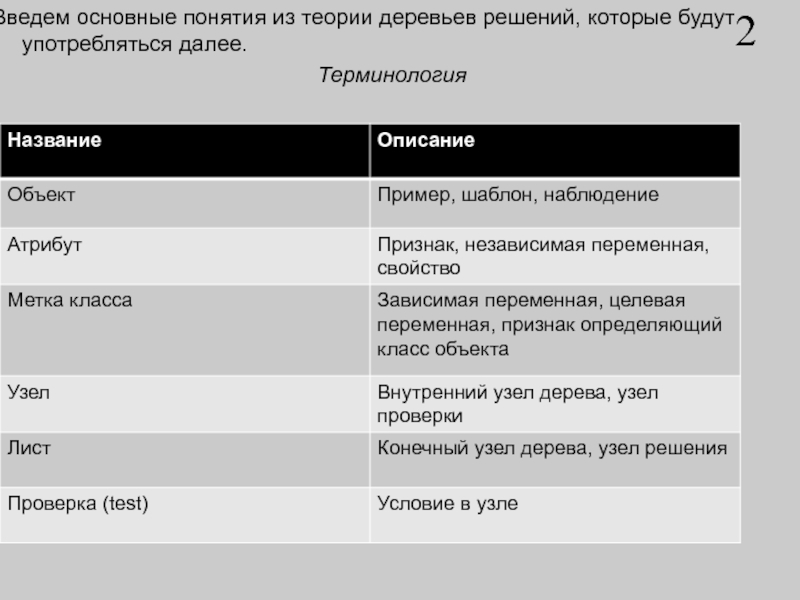
Введем
основные понятия из теории деревьев решений, которые будут употребляться далее.
Терминология
2
Слайд 4Деревья решений – это способ представления правил в иерархической, последовательной
структуре, где каждому объекту соответствует единственный узел, дающий решение.
Под правилом
понимается логическая конструкция, представленная в виде "если ... то ...".Область применения деревья решений в настоящее время широка, но все задачи, решаемые этим аппаратом могут быть объединены в следующие три класса:
Описание данных: Деревья решений позволяют хранить информацию о данных в компактной форме, вместо них мы можем хранить дерево решений, которое содержит точное описание объектов.
Классификация: Деревья решений отлично справляются с задачами классификации, т.е. отнесения объектов к одному из заранее известных классов. Целевая переменная должна иметь дискретные значения.
Регрессия: Если целевая переменная имеет непрерывные значения, деревья решений позволяют установить зависимость целевой переменной от независимых(входных) переменных. Например, к этому классу относятся задачи численного прогнозирования (предсказания значений целевой переменной).
3
Слайд 5ТЕМА 2. ЗНАНИЯ И ИХ ПРЕДСТАВЛЕНИЕ В СИСТЕМАХ ИИ
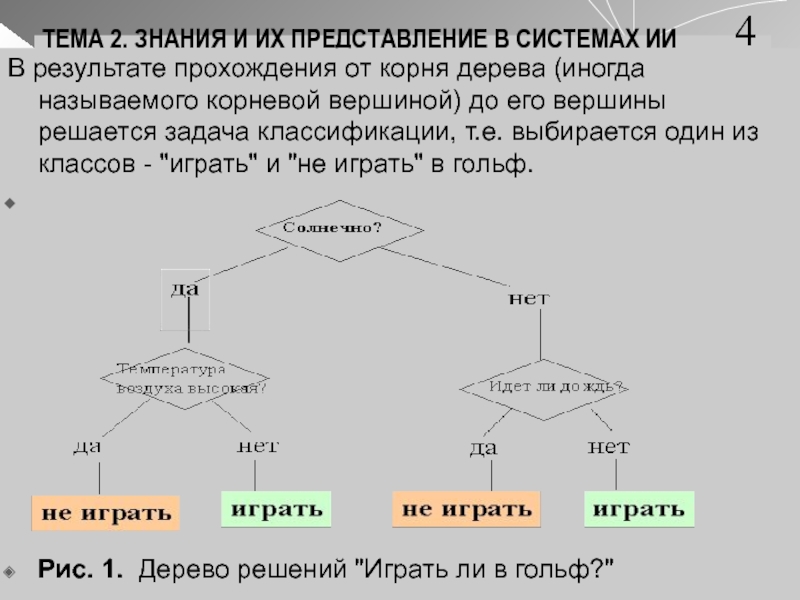
В
результате прохождения от корня дерева (иногда называемого корневой вершиной) до
его вершины решается задача классификации, т.е. выбирается один из классов - "играть" и "не играть" в гольф.Рис. 1. Дерево решений "Играть ли в гольф?"
4
Слайд 7ТЕМА 2. ЗНАНИЯ И ИХ ПРЕДСТАВЛЕНИЕ В СИСТЕМАХ ИИ
Как
построить дерево решений?
Пусть нам задано некоторое обучающее множество T, содержащее
объекты (примеры), каждый из которых характеризуется m атрибутами , причем один из них указывает на принадлежность объекта к определенному классу.Идею построения деревьев решений из множества T, впервые высказанную Хантом, приведем по Р. Куинлену (R. Quinlan).
Пусть через {C1, C2, ... Ck} обозначены классы (значения метки класса), тогда существуют 3 ситуации:
1. множество T содержит один или более примеров, относящихся к одному классу Ck. Тогда дерево решений для Т – это лист, определяющий класс Ck;
6
Слайд 8ТЕМА 2. ЗНАНИЯ И ИХ ПРЕДСТАВЛЕНИЕ В СИСТЕМАХ ИИ
2.
множество T не содержит ни одного примера, т.е. пустое множество.
Тогда это снова лист, и класс, ассоциированный с листом, выбирается из другого множества отличного от T, скажем, из множества, ассоциированного с родителем;3. множество T содержит примеры, относящиеся к разным классам. В этом случае следует разбить множество T на некоторые подмножества. Для этого выбирается один из признаков, имеющий два и более отличных друг от друга значений O1, O2, ... On.
T разбивается на подмножества T1, T2, ... Tn, где каждое подмножество Ti содержит все примеры, имеющие значение Oi для выбранного признака. Это процедура будет рекурсивно продолжаться до тех пор, пока конечное множество не будет состоять из примеров, относящихся к одному и тому же классу.
7
Слайд 9ТЕМА 2. ЗНАНИЯ И ИХ ПРЕДСТАВЛЕНИЕ В СИСТЕМАХ ИИ
Вышеописанная
процедура лежит в основе многих современных алгоритмов построения деревьев решений,
этот метод известен еще под названием разделения и захвата (divide and conquer). При использовании данной методики, построение дерева решений будет происходит сверху вниз.Поскольку все объекты были заранее отнесены к известным нам классам, такой процесс построения дерева решений называется обучением с учителем (supervised learning) или индуктивным обучением или индукцией деревьев (tree induction).
На сегодняшний день существует значительное число алгоритмов, реализующих деревья решений CART, C4.5, NewId, ITrule, CHAID, CN2 алгоритм Microsoft Decision Trees содержащейся в составе аналитических служб Microsoft SQL Server 2000 (Enterprise Edition, Standard Edition или Personal Edition).
Но наибольшее распространение получили следующие два:
CART (Classification and Regression Tree) – это алгоритм построения бинарного дерева решений – дихотомической классификационной модели. Каждый узел дерева при разбиении имеет только двух потомков. Как видно из названия алгоритма, решает задачи классификации и регрессии.
C4.5 – алгоритм построения дерева решений, количество потомков у узла не ограничено. Решает только задачи классификации.
8
Слайд 10ТЕМА 2. ЗНАНИЯ И ИХ ПРЕДСТАВЛЕНИЕ В СИСТЕМАХ ИИ
Преимущества
деревьев решений
1) Интуитивность деревьев решений.
Классификационная модель, представленная в виде дерева
решений, является интуитивной и упрощает понимание решаемой задачи. Результат работы алгоритмов конструирования деревьев решений, в отличие, например, от нейронных сетей, представляющих собой "черные ящики", легко интерпретируется пользователем. Это свойство деревьев решений не только важно при отнесении к определенному классу нового объекта, но и полезно при интерпретации модели классификации в целом. Дерево решений позволяет понять и объяснить, почему конкретный объект относится к тому или иному классу.2) Деревья решений дают возможность извлекать правила из базы данных на естественном языке. Пример правила: Если Возраст > 40 и есть дом, то выдать кредит.
3) Деревья решений позволяют создавать классификационные модели в тех областях, где аналитику достаточно сложно формализовать знания.
9
Слайд 11ТЕМА 2. ЗНАНИЯ И ИХ ПРЕДСТАВЛЕНИЕ В СИСТЕМАХ ИИ
4)
Алгоритм конструирования дерева решений не требует от пользователя выбора входных атрибутов (независимых
переменных). На вход алгоритма можно подавать все существующие атрибуты, алгоритм сам выберет наиболее значимые среди них, и только они будут использованы для построения дерева. В сравнении, например, с нейронными сетями, это значительно облегчает пользователю работу, поскольку в нейронных сетях выбор количества входных атрибутов существенно влияет на время обучения.5) Точность моделей, созданных при помощи деревьев решений, сопоставима с другими методами построения классификационных моделей (статистические методы, нейронные сети).
6) Быстрый процесс обучения. На построение классификационных моделей при помощи алгоритмов конструирования деревьев решений требуется значительно меньше времени, чем, например, на обучение нейронных сетей.
Большинство алгоритмов конструирования деревьев решений имеют возможность специальной обработки пропущенных значений.
10
Слайд 12ТЕМА 2. ЗНАНИЯ И ИХ ПРЕДСТАВЛЕНИЕ В СИСТЕМАХ ИИ
Процесс
конструирования дерева решений
В ходе создания дерева решаются вопросы выбора критерия расщепления и остановки обучения
(если это предусмотрено алгоритмом). В ходе этапа сокращения дерева решается вопрос отсечения некоторых его ветвей.Критерий расщепления
Процесс создания дерева происходит сверху вниз, т.е. является нисходящим. В ходе процесса алгоритм должен найти такой критерий расщепления, иногда также называемый критерием разбиения, чтобы разбить множество на подмножества, которые бы ассоциировались с данным узлом проверки. Каждый узел проверки должен быть помечен определенным атрибутом. Существует правило выбора атрибута: он должен разбивать исходное множество данных таким образом, чтобы объекты подмножеств, получаемых в результате этого разбиения, являлись представителями одного класса или же были максимально приближены к такому разбиению.
Существуют различные критерии расщепления. Наиболее известные - мера энтропии и индекс Gini. Если дано множество T, включающее примеры из n классов, индекс Gini, т.е. gini(T), определяется по формуле:
где T - текущий узел, pj - вероятность класса j в узле T, n - количество классов.
11
Слайд 13ТЕМА 2. ЗНАНИЯ И ИХ ПРЕДСТАВЛЕНИЕ В СИСТЕМАХ ИИ
Остановка
построения дерева
Правило остановки должно определить, является ли рассматриваемый узел внутренним узлом, при
этом он будет разбиваться дальше, или же он является конечным узлом, т.е. узлом решением.Остановка - такой момент в процессе построения дерева, когда следует прекратить дальнейшие ветвления.
1) "ранняя остановка" (prepruning), она определяет целесообразность разбиения узла. Преимущество использования такого варианта - уменьшение времени на обучение модели. Однако здесь возникает риск снижения точности классификации. Поэтому рекомендуется "вместо остановки использовать отсечение».
2) ограничение глубины дерева. В этом случае построение заканчивается, если достигнута заданная глубина.
3) задание минимального количества примеров, которые будут содержаться в конечных узлах дерева. При этом варианте ветвления продолжаются до того момента, пока все конечные узлы дерева не будут чистыми или будут содержать не более чем заданное число объектов.
12
Слайд 14ТЕМА 2. ЗНАНИЯ И ИХ ПРЕДСТАВЛЕНИЕ В СИСТЕМАХ ИИ
Сокращение дерева или отсечение ветвей
Решением проблемы слишком ветвистого дерева
является его сокращение путем отсечения (pruning) некоторых ветвей.Качество классификационной модели, построенной при помощи дерева решений, характеризуется двумя основными признаками: точностью распознавания и ошибкой.
Точность распознавания рассчитывается как отношение объектов, правильно классифицированных в процессе обучения, к общему количеству объектов набора данных, которые принимали участие в обучении.
Ошибка рассчитывается как отношение объектов, неправильно классифицированных в процессе обучения, к общему количеству объектов набора данных, которые принимали участие в обучении.
Отсечение ветвей или замену некоторых ветвей поддеревом следует проводить там, где эта процедура не приводит к возрастанию ошибки. Процесс проходит снизу вверх, т.е. является восходящим. Деревья, получаемые после отсечения некоторых ветвей, называют усеченными.
Если такое усеченное дерево все еще не является интуитивным и сложно для понимания, используют извлечение правил, которые объединяют в наборы для описания классов. Каждый путь от корня дерева до листа дает одно правило. Условиями правила являются проверки на внутренних узлах дерева.
13
Слайд 15ТЕМА 2. ЗНАНИЯ И ИХ ПРЕДСТАВЛЕНИЕ В СИСТЕМАХ ИИ
Мы
рассмотрели метод деревьев решений; являющийся иерархическим, гибким средством предсказания принадлежности
объектов к определенному классу или прогнозирования значений числовых переменных.Качество работы рассмотренного метода деревьев решений зависит как от выбора алгоритма, так и от набора исследуемых данных. Несмотря на все преимущества данного метода, следует помнить, что для того, чтобы построить качественную модель, необходимо понимать природу взаимосвязи между зависимыми и независимыми переменными и подготовить достаточный набор данных.
14
Слайд 16ТЕМА 2. ЗНАНИЯ И ИХ ПРЕДСТАВЛЕНИЕ В СИСТЕМАХ ИИ
4
Продукционные модели
Продукционная модель представления знаний является одной из самых распространенных.
В системах продукций знания представляются с помощью наборов ЕСЛИ А1,А2,… Аn ТО В
Такая запись означает, что «если выполняются все условия от А1 до Аn (являются истинными), тогда следует выполнить действие В» Продукции также могут пониматься как «ситуация – действие», «причина – следствие», «условие – заключение». Условия А1,А2,… Аn обычно называют фактами. С помощью фактов обычно описывается текущее состояние предметной области. Действие В может трактоваться как добавление нового факта в описание текущего состояния предметной области.
Множество продукционных правил образует базу правил, которая представляет обособленный фрагмент знаний о решаемой проблеме. Психологи называют такие фрагменты чанками. Считается, что чанк – это объективно – существующая единица знаний, выделяемая человеком в процессе познания окружающего мира.
15
Слайд 17ТЕМА 2. ЗНАНИЯ И ИХ ПРЕДСТАВЛЕНИЕ В СИСТЕМАХ ИИ
4
Продукционные модели
Пример 1. В качестве примера рассмотрим правило, взятое из
базы знаний экспертной системы MYCIN, предназначенной для диагностики инфекционных заболеваний крови.ЕСЛИ:
Место выделения культуры – кровь И
Реакция микроорганизма – грамоотрицательтная И
Форма микроорганизма – палочка И
Пациент относится к группе риска
ТО
С уверенностью 0,6 название микроорганизма pseudomonia aeruginosa.
16
Слайд 18ТЕМА 2. ЗНАНИЯ И ИХ ПРЕДСТАВЛЕНИЕ В СИСТЕМАХ ИИ
4
Продукционные модели
С каждым правилом связывается некоторое число, принимающее значение от
–1 до 1. Число выражает степень достоверности следствия и называется коэффициентом уверенности. Это означает, что система имеет дело с неточными и ненадежными фактами.
В базе знаний MYCIN факты представляются с помощью триплета: объект-атрибут-значение, «культура – место – кровь» для факта 1. Если в процессе активации правила первые четыре факта окажутся истинными, то в базу знаний поступит новый факт, представляемый триплетом объект-атрибут-значение.
17
Слайд 19ТЕМА 2. ЗНАНИЯ И ИХ ПРЕДСТАВЛЕНИЕ В СИСТЕМАХ ИИ
4
Продукционные модели
Пример 2. Задача технической диагностики. Пусть требуется установить причину
неисправности электрической плиты. Одно из правил экспертной системы может иметь вид:ЕСЛИ:
лампа светится И
плита холодная
ТО нагреватель неисправен
18
Слайд 20ТЕМА 2. ЗНАНИЯ И ИХ ПРЕДСТАВЛЕНИЕ В СИСТЕМАХ ИИ
4
Продукционные модели
Во многих случаях правило-продукцию записывают в обобщенной форме:
Rnj : (Pr, Bc, AB, Ac), гдеRnj - идентификатор j – той продукции в n-ном наборе продукций;
Pr - приоритет правила продукции;
Bc – предусловие применимости ядра продукции, представляющее предикат, при выполнении которого активизируется ядро продукции;
AB –ядро продукции;
Ac – постусловия продукции, определяющее действия и процедуры, которые необходимо выполнить после выполнения ядра продукции.
19
Слайд 21ТЕМА 2. ЗНАНИЯ И ИХ ПРЕДСТАВЛЕНИЕ В СИСТЕМАХ ИИ
4
Продукционные модели
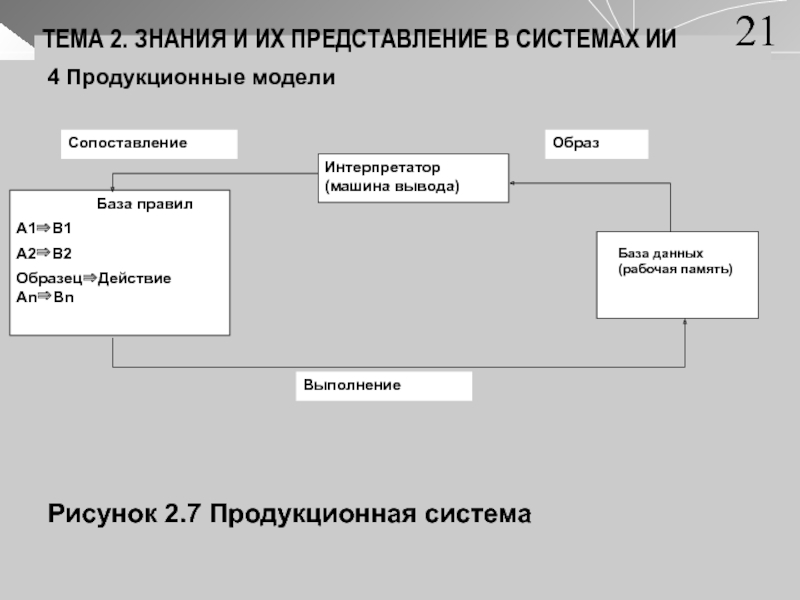
В общем случае, продукционная система включает компоненты:
Базу продукционных правил
Базу
данных (рабочая память)Интерпретатор
Предпосылки правила (левая часть) часто рассматривается как образец.
Образец – это некоторая информационная структура, определяющая обобщенную ситуацию (условие или состояние) окружающей действительности, при которой активизируется правило.
Рабочая память (БД) отражает конкретные ситуации (состояния или условия), возникающие во внешней среде.
Информационная структура, представляющая конкретную ситуацию во внешней среде называется образом.
Интерпретатор реализует логический вывод. Процесс вывода является циклическим и называется поиском по образцу. Рассмотрим его в упрощенной форме. Текущее состояние моделируемой ПО отражается в рабочей памяти в виде совокупности образов, каждый из которых представляется посредством фактов.
20
Слайд 22ТЕМА 2. ЗНАНИЯ И ИХ ПРЕДСТАВЛЕНИЕ В СИСТЕМАХ ИИ
4
Продукционные модели
Рисунок 2.7 Продукционная система
21
Слайд 23ТЕМА 2. ЗНАНИЯ И ИХ ПРЕДСТАВЛЕНИЕ В СИСТЕМАХ ИИ
4
Продукционные модели
Рабочая память инициализируется фактами, описывающими задачу.
Затем выбираются те
правила, для которых образцы, представляемые предпосылками правил, сопоставимы с образами в рабочей памяти.Данные правила образуют конфликтное множество. Все правила из конфликтного множества могут быть активизированы в любой момент.
В соответствии с выбранным стратегией разрешения конфликтов активизируется одно из этих правил.
Выполнение действия, содержащегося в заключении правила, приводят к изменению состояния рабочей памяти (образа)
В дальнейшем цикл управления выводом повторяется (переход на шаг 2).
Указанный процесс завершается, когда не окажется правил, предпосылки которых сопоставимы с образами рабочей памяти.
22
Слайд 24ТЕМА 2. ЗНАНИЯ И ИХ ПРЕДСТАВЛЕНИЕ В СИСТЕМАХ ИИ
4
Продукционные модели
Процесс вывода, основанный на поиске по образцу, состоит из
четырех шагов:выбор образа;
сопоставление образа с образцом и формирование конфликтного набора правил;
разрешение конфликтов (выбор конкретного правила);
выполнение правила.
23
Слайд 25ТЕМА 2. ЗНАНИЯ И ИХ ПРЕДСТАВЛЕНИЕ В СИСТЕМАХ ИИ
4
Продукционные модели
Пример 3. Поясним процесс функционирования продукционной системы на простом
примере сортировки символов в строке, состоящей из букв a,b,c. Задана строка cbca (образ) и задано множество продукций:
ba ab
ca ac
cbbc
Необходимо провести сортировку по трем заданным правилам.
Если образец, заданный предпосылкой правила, сопоставим с частью сортируемой строки, то правило активизируется.
В результате этого подстрока, которая совпала с условием правила, замещается подстрокой из заключительной части правила. Конфликтное множество на первом шаге состоит из правил 2 и 3. Процесс завершается, когда не оказывается правил, предпосылки которых сопоставимы с подстроками (к строке abcc нельзя применить ни одно из указанных правил).
24
Слайд 26ТЕМА 2. ЗНАНИЯ И ИХ ПРЕДСТАВЛЕНИЕ В СИСТЕМАХ ИИ
4
Продукционные модели
Рисунок 2.8 Сортировка строки с помощью правил-продукций
25
Слайд 27ТЕМА 2. ЗНАНИЯ И ИХ ПРЕДСТАВЛЕНИЕ В СИСТЕМАХ ИИ
4
Продукционные модели
Рассматривая исходную и отсортированную строки как начальное и конечное
состояние задачи, а продукционные правила как операторы, преобразующие одно состояние задачи в другое, приходим к выводу, что поиск решения в продукционных системах соответствует поиску в пространстве состояний. На рис. 2.8 изображено дерево состояний задачи. Здесь вершины дерева соответствуют промежуточным состояниям сортируемой строки, а ребра – правилам-продукциям
Продукционные системы были предложены американским математиком Э. Постом в 1943 году и рассматривались как модель организации вычислительного процесса.
При этом правило (продукция) трактовалось как оператор замены одной цепочки литер в некотором слове на другую.
26
Слайд 28ТЕМА 2. ЗНАНИЯ И ИХ ПРЕДСТАВЛЕНИЕ В СИСТЕМАХ ИИ
4
Продукционные модели
Интересные результаты были получены А. Ньюэллом и Г. Саймоном
при разработке системы GPS. Они установили, что продукции соответствуют элементам знаний, накапливаемым в долговременной памяти человека. Такие элементы знаний активизируются, если возникает соответствующая ситуация (по образцу).
Новые элементы знаний могут накапливаться в памяти без необходимости перезаписывания уже существующих элементов.
Рабочая память продукционных систем аналогична кратковременной памяти человека, который удерживает в центре внимания только текущую ситуацию. Содержимое рабочей памяти, как правило, не сохраняется после решения задач.
Благодаря указанной аналогии продукционные модели представления знаний получили широкое распространение в экспертных системах, моделирующих решение задач человеком – экспертом в той или иной области.
27
Слайд 29ТЕМА 2. ЗНАНИЯ И ИХ ПРЕДСТАВЛЕНИЕ В СИСТЕМАХ ИИ
4
Продукционные модели
Управление выводом в продукционной системе
В ходе решения проблем
машина вывода (интерпретатор) выполняет две задачи - собственно логический вывод и управление выводом.Логический вывод достаточно простой и реализуется на основе процедуры поиска по образцу.
Управление выводом предполагает решение двух вопросов:
с чего следует начать процесс вывода?
как поступить, если на некотором шаге вывода возможен выбор вариантов его продолжения?
Ответ на первый вопрос приводит к прямой и обратной цепочке рассуждений.
А на второй вопрос - к механизму разрешения конфликтов в продукционной системе.
28
Слайд 30ТЕМА 2. ЗНАНИЯ И ИХ ПРЕДСТАВЛЕНИЕ В СИСТЕМАХ ИИ
4
Продукционные модели
Прямой вывод начинается с задания исходных данных решаемой задачи,
которые фиксируются в виде фактов в рабочей памяти системы. Правила применяются к исходным данным и обеспечивают генерацию новых фактов, добавляемых в рабочую память. Процесс продолжается, пока не будет получено целевое состояние рабочей памяти.Обратный вывод начинается с целевого утверждения, которое фиксируется в рабочей памяти. Затем отыскивается правило-продукция, заключение которого сопоставимо с целью. Условие данного правила помещаются в рабочую память и становятся новой подцелью. Процесс повторяется до тех пор, пока в рабочей памяти не будут получены факты, подтверждающие целевое утверждение.
29
Слайд 31ТЕМА 2. ЗНАНИЯ И ИХ ПРЕДСТАВЛЕНИЕ В СИСТЕМАХ ИИ
4
Продукционные модели
Управление разрешением конфликтов
Порядок активизации правил конфликтного множества определяется выбранной
стратегией разрешения конфликтов. Конфликтное множество можно представить в виде упорядоченного списка, при этом конфликтные правила могут дописываться в конец этого списка. Простые стратегии основаны на том, что выбирается либо первое, либо последнее правило из этого списка. Другими принципами, на которых основываются стратегии, используемые при разрешении конфликтов, являются:Принцип «стопки книг» заключается в том, что список конфликтующих правил упорядочивается в соответствии с частотой использования продукций в прошлом. В первую очередь выбирается продукция, которая использовалась чаще всех.
Принцип наиболее длинного условия отдает приоритет той продукции, которая содержит наибольшее число предпосылок в левой части, т.е. наиболее длинное условие.
Принцип метапродукций основан на введении в базу знаний специальных метаправил, упорядочивающих процесс разрешения конфликтов.
Принцип приоритетного выбора связывает с каждой продукцией статический или динамический приоритет Pr , определяющий порядок ее активации.
30
Слайд 32ТЕМА 2. ЗНАНИЯ И ИХ ПРЕДСТАВЛЕНИЕ В СИСТЕМАХ ИИ
4
Продукционные модели
Достоинства продукционных моделей
Универсальность: практически любая область знаний может быть
представлена в продукционной форме.Модульность: каждая продукция представляет собой элемент знаний о предметной области. Удаление одних и добавление других продукций (модулей) выполняется независимо.
Декларативность: продукции определяют ситуации ПО, а не механизм управления.
Естественность процесса вывода заключений, который во многом аналогичен процессу рассуждений эксперта.
Асинхронность и естественный параллелизм, который делает их весьма перспективными для реализации на параллельных ЭВМ.
31
Слайд 33ТЕМА 2. ЗНАНИЯ И ИХ ПРЕДСТАВЛЕНИЕ В СИСТЕМАХ ИИ
4
Продукционные модели
Недостатки продукционных систем
Процесс вывода имеет низкую эффективность, так как
при большом числе продукций значительное время затрачивается на непроизводительную проверку условий применения правил.Проверка непротиворечивости системы продукции становится весьма сложной из-за неопределенности выбора выполняемой продукции из конфликтного множества.
Возникновение побочных эффектов, непредсказуемых при изменении старых и добавлении новых правил.
32