с неизвестным параметром θ. До сих пор мы занимались «точечным
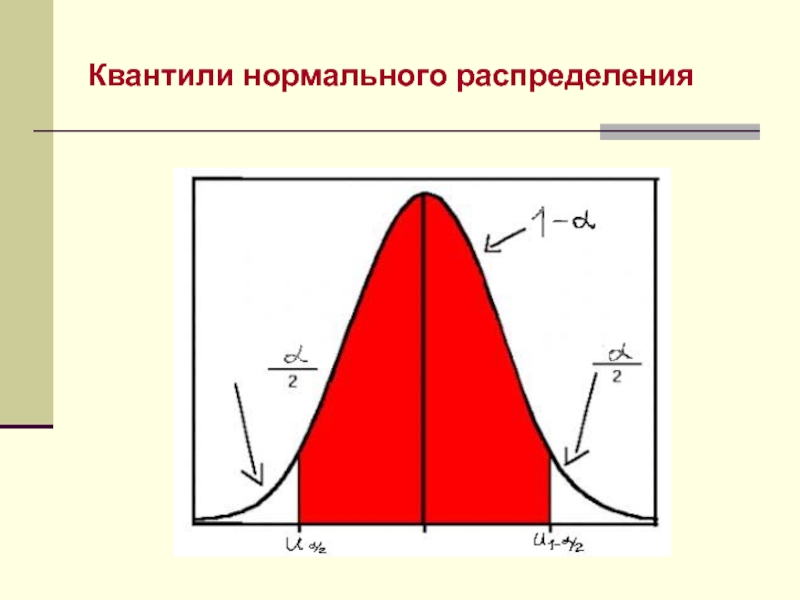
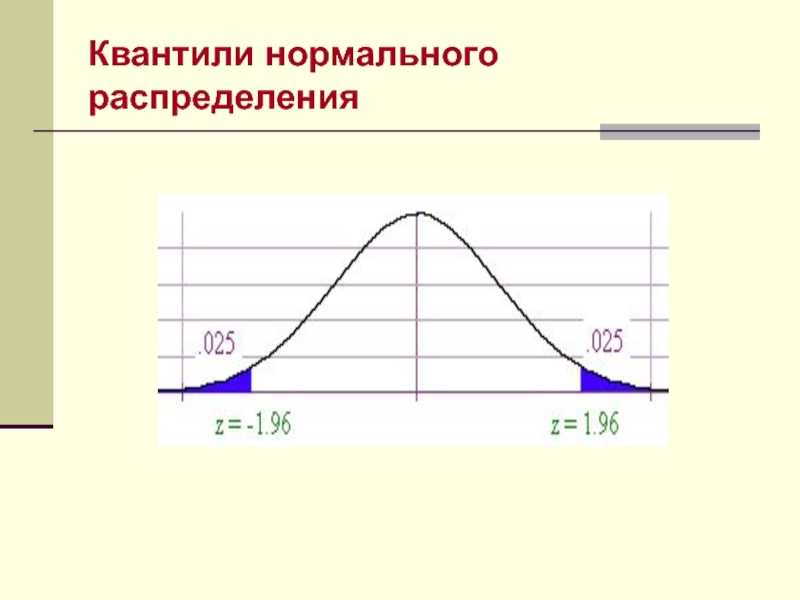
оцениванием» неизвестного параметра — находили приближенное значение параметра ( его оценку).Существует другой подход к оцениванию, при котором мы указываем интервал, накрывающий параметр с заданной наперед вероятностью. Такой подход называется «интервальным оцениванием».
Интервальное оценивание
Интервальное оценивание