Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Использование корреляционно-регрессионного анализа в управлении предприятием
Содержание
- 1. Использование корреляционно-регрессионного анализа в управлении предприятием
- 2. Корреляционно-регрессионный анализ как общее понятие включает в
- 3. Корреляционный анализ
- 4. Относительно формы связи различают:А) линейную корреляцию -
- 5. Регрессионный анализ - заключается в определении аналитического
- 6. Относительно формы зависимости различают:А) линейную регрессию, выражаемую
- 7. По направлению связи различают:прямую регрессию(положительную), возникающую при
- 8. Требования, при которых соблюдается адекватность уравнения регрессииСовокупность
- 9. Основной предпосылкой корреляционного анализа является необходимость подчинения
- 10. Рассмотрим метод линейного коэффициента корреляции более обширней.
- 11. Коэффициент ранговой корреляции КендаллаПрименяется для выявления взаимосвязи
- 12. Коэффициент ранговой корреляции СпирменаКаждому показателю X и
- 13. Коэффициент корреляции знаков ФехнераПодсчитывается количество совпадений и
- 14. Построение моделей и использование их на практике Результаты деятельности промышленных предприятий
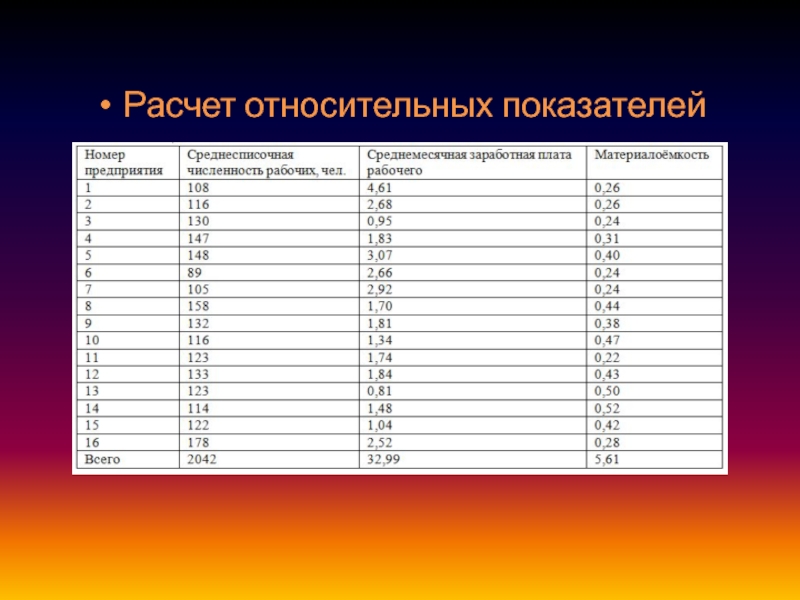
- 15. Расчет относительных показателей
- 16. Определение тесноты взаимосвязи между показателями с помощью
- 17. Слайд 17
- 18. Из полученного значения можно сделать вывод, что
- 19. Определение тесноты парной связи и формы для всей статистической совокупности.
- 20. Рассчитаем линейный коэффициент корреляции:Так как коэффициент положительный,
- 21. График уравнений линейной регрессии для данных статистической совокупностиНайдём параметры уравнения линейной регрессии:
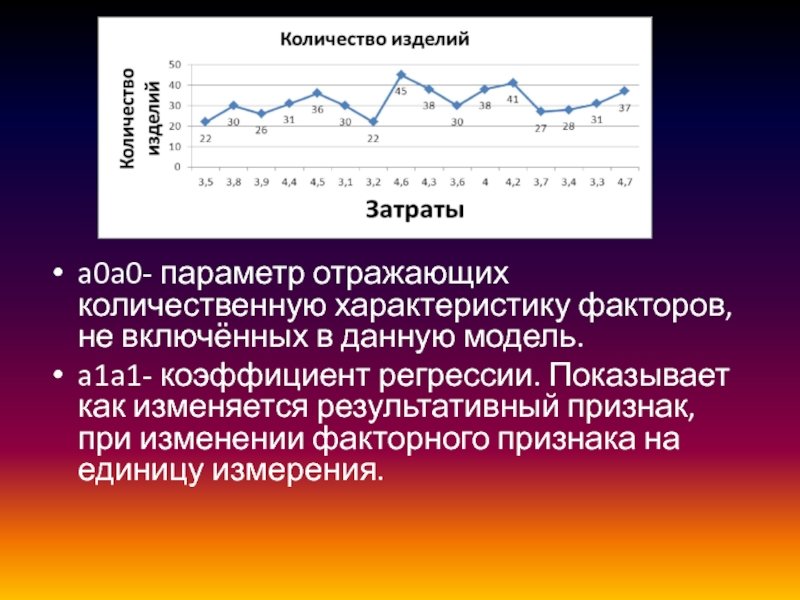
- 22. a0a0- параметр отражающих количественную характеристику факторов, не
- 23. Таблица промежуточных расчётов
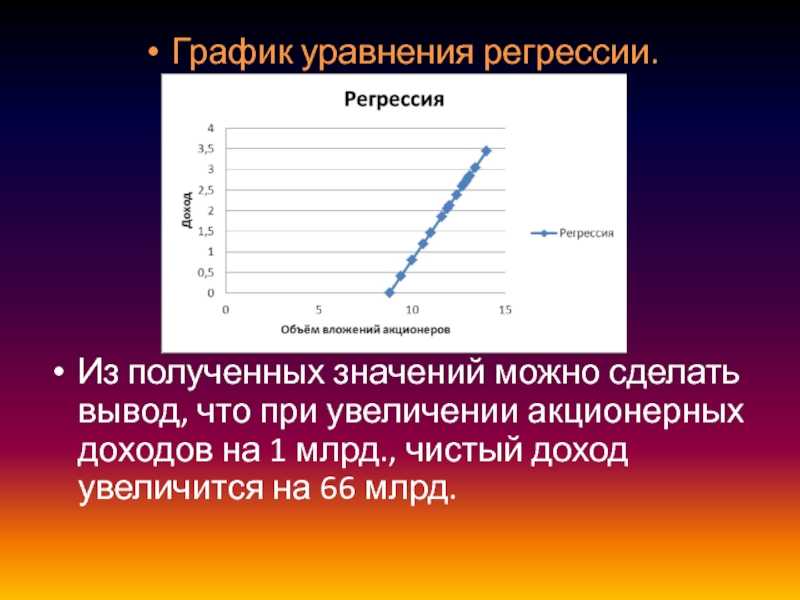
- 24. График уравнения регрессии.Из полученных значений можно сделать
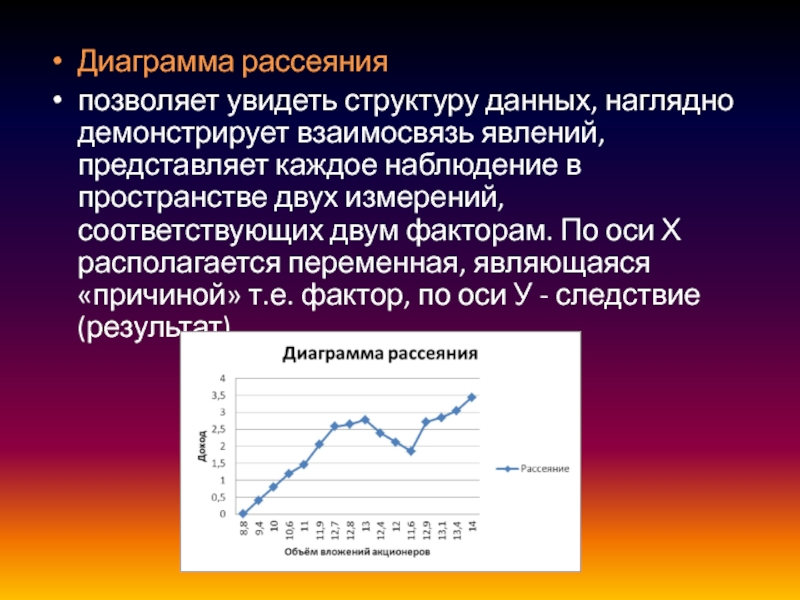
- 25. Диаграмма рассеянияпозволяет увидеть структуру данных, наглядно демонстрирует
- 26. СПАСИБО ЗА ВНИМАНИЕ!
- 27. Скачать презентанцию
Корреляционно-регрессионный анализ как общее понятие включает в себя измерение тесноты, направления связи и установление аналитического выражения (формы) связи (регрессионный анализ). Этот метод содержит две составляющие части - корреляционный анализ и регрессионный
Слайды и текст этой презентации
Слайд 3
Корреляционный анализ - это
количественный метод определения тесноты и направления взаимосвязи между выборочными переменными
величинами.В статистике принято различать следующие варианты зависимостей:
Парная корреляция - связь между двумя признаками (результативным и факторным или двумя факторными).
Частная корреляция - зависимость между результативным и одним факторным признаками при фиксированном значении других факторных признаков.
Множественная корреляция - зависимость результативного и двух или более факторных признаков, включенных в исследование.
Слайд 4Относительно формы связи различают:
А) линейную корреляцию - характеризует тесноту и
направление связи между двумя коррелируемыми признаками, в случае наличия между
ними линейной зависимости.Б) нелинейную - корреляция, при которой отношение степени изменения одной переменной к степени изменения другой переменной является изменяющейся величиной.
Слайд 5Регрессионный анализ - заключается в определении аналитического выражения связи, в
котором изменение одной величины обусловлено влиянием одной или нескольких величин,
а множество всех прочих факторов, также оказывающих влияние на зависимую величину, принимается за постоянные и средние значения. Регрессия может быть однофакторной(парной) и многофакторной(множественной).Слайд 6Относительно формы зависимости различают:
А) линейную регрессию, выражаемую линейной функцией. При
этой форме зависимости между исследуемыми переменными объективно существуют линейные соотношения.
Выражается уравнением прямой вида:Б) нелинейную регрессию, выражаемую нелинейной функцией. В этом случае между исследуемыми экономическими явлениями объективно существуют нелинейные соотношения. Выражается уравнением вида:
Парабола -
Гипербола -
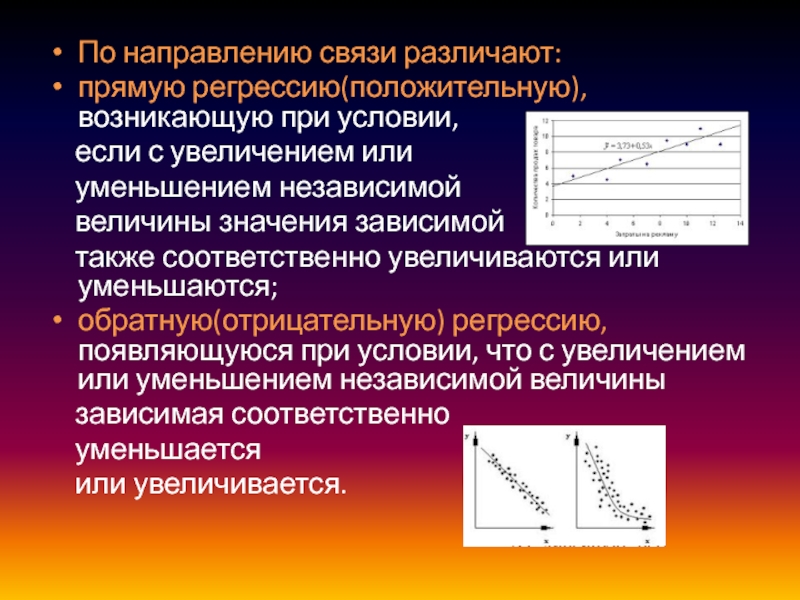
Слайд 7По направлению связи различают:
прямую регрессию(положительную), возникающую при условии,
если с увеличением или
уменьшением независимой
величины значения зависимой также соответственно увеличиваются или уменьшаются;
обратную(отрицательную) регрессию, появляющуюся при условии, что с увеличением или уменьшением независимой величины
зависимая соответственно
уменьшается
или увеличивается.
Слайд 8Требования, при которых соблюдается адекватность уравнения регрессии
Совокупность исследуемых исходных данных
должна быть однородной.
Возможность описания моделируемого явления одним или несколькими уравнениями
причинно-следственных связей.Все факторные признаки должны иметь количественное (цифровое) выражение.
Наличие достаточно большого объёма исследуемой выборочной совокупности.
Причинно-следственные связи между явлениями и процессами следует описывать линейной или приводимой к линейной формами зависимости.
Отсутствие количественных ограничений на параметры моделей связи.
Постоянство территориальной и временной структуры изучаемой продукции.
Слайд 9Основной предпосылкой корреляционного анализа является необходимость подчинения совокупности значений всех
факторных (x1, x2,…xk) и результативного (У) признаков k-мерному нормальному закону
распределения или близость к нему.Целью регрессионного анализа является оценка функциональной зависимости условного среднего значения результативного признака (У) от факторных (x1, x2,….xk).
Основной предпосылкой регрессионного анализа является то, что только результативный признак подчиняется нормальному закону распределения, а факторные признаки могут иметь произвольный закон распределения.
Слайд 10Рассмотрим метод линейного коэффициента корреляции более обширней. Линейный коэффициент корреляции
разработали Карл Пирсон, Фрэнсис Эджуорт и Рафаэль Уэлдон в 90-х
годах XIX века и рассчитывается по формуле:Где Х - факторный признак У - результативный
Коэффициент корреляции изменяется по модулю от -1 до 1.
1 - идеальная положительная связь Все точки данных располагаются строго на прямой линии, направленной вверх и в право.
Близко к 1 - сильная положительная взаимосвязь. Точки данных плотно сгруппированы вокруг прямой линии, направленной вверх и вправо.
Близко к 0 (положительно) - отсутствие взаимосвязи. Случайное облако точек данных. Не имеет чёткой направленности ни вверх, ни вниз при движении вправо.
Близко к 0 (отрицательно) - незначительная отрицательная взаимосвязь. Точки данных образуют случайное облако с незначительной ориентацией вниз и вправо.
Близко к -1 - сильная отрицательная взаимосвязь. Точки данных плотно сгруппированы вокруг прямой линии, направленной вниз и вправо.
-1 - Идеальная взаимосвязь, все точки располагаются строго на прямой.
Не определено - точки данных располагаются строго на горизонтали или на вертикальной линии.
Слайд 11Коэффициент ранговой корреляции Кендалла
Применяется для выявления взаимосвязи между количественными или
качественными показателями, если их можно ранжировать. Значения показателя X выставляют
в порядке возрастания и присваивают им ранги. Ранжируют значения показателя Y и рассчитывают коэффициент корреляции Кендалла:где S=P-Q
P - суммарное число наблюдений, следующих за текущими наблюдениями с большим значением рангов Y.
Q- суммарное число наблюдений, следующих за текущими наблюдениями с меньшим значением рангов Y. (равные ранги не учитываются)
Слайд 12Коэффициент ранговой корреляции Спирмена
Каждому показателю X и Y присваивается ранг.
На основе полученных рангов рассчитываются их разности и вычисляется коэффициент
корреляции Спирмена:Слайд 13Коэффициент корреляции знаков Фехнера
Подсчитывается количество совпадений и несовпадений знаков отклонений
значений показателей от их среднего значения.
C - число пар, у
которых знаки отклонений значений от их средних совпадают.H - число пар, у которых знаки отклонений значений от их средних не совпадают.
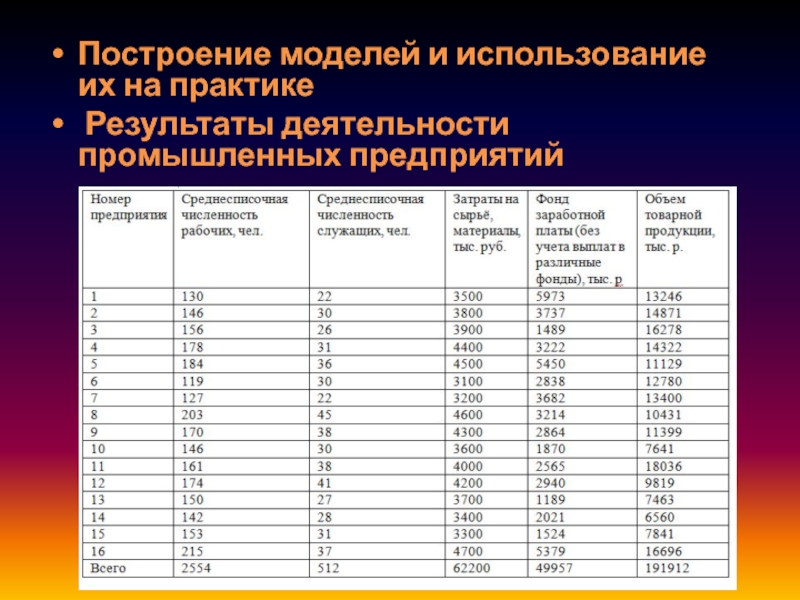
Слайд 14Построение моделей и использование их на практике
Результаты деятельности промышленных предприятий
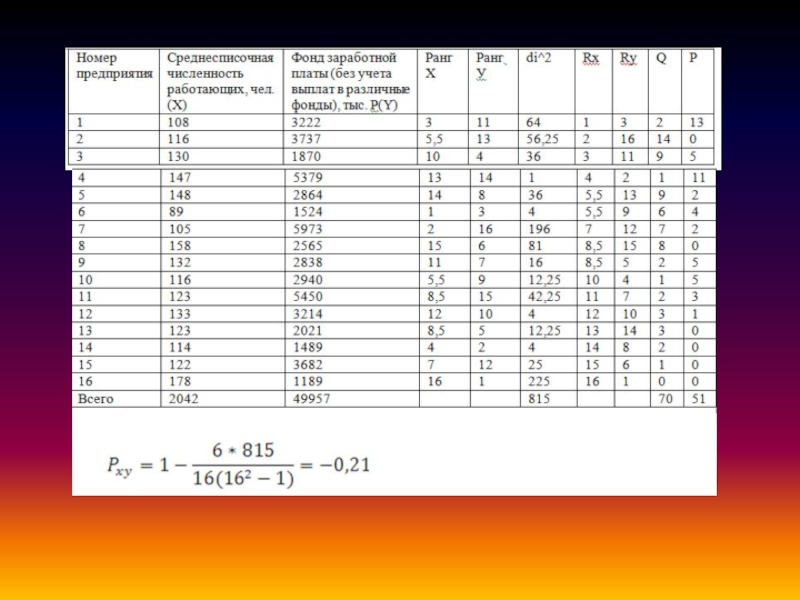
Слайд 16Определение тесноты взаимосвязи между показателями с помощью коэффициента ранговой корреляции.
Определим
тесноту связи между показателями: фонд заработной платы, среднесписочная численность рабочих,
используя коэффициент ранговой корреляции. Этот коэффициент представляет собой показатель, характеризующий статистическую связь двух признаков, измеряемых в порядковой шкале. Для признаков, измеренных в порядковых шкалах, наиболее известным является коэффициент ранговой корреляции Спирмена:di 2 - квадрат разности рангов