Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Исследование функции с помощью производной
Содержание
- 1. Исследование функции с помощью производной
- 2. 1. Область определения функции:D (y) = (-∞;-1);(-1;+∞).
- 3. 2. Множество значений функции:E (y) = (-∞;0,25].
- 4. 3. Исследование на четность:Т. к. не выполняются
- 5. 4. Исследование на периодичность:Функция не является периодической.
- 6. 5. Нули функции:Уравнение имеет корень
- 7. 6. Пересечение с осью OY:
- 8. 7. Первая производная функции:
- 9. 8. Критические точки функции (первая производная):
- 10. 9. Промежутки монотонности функции:Значит, промежутки монотонности:-11+--xy (x)(-1; 1];(-∞; -1);[1; +∞).
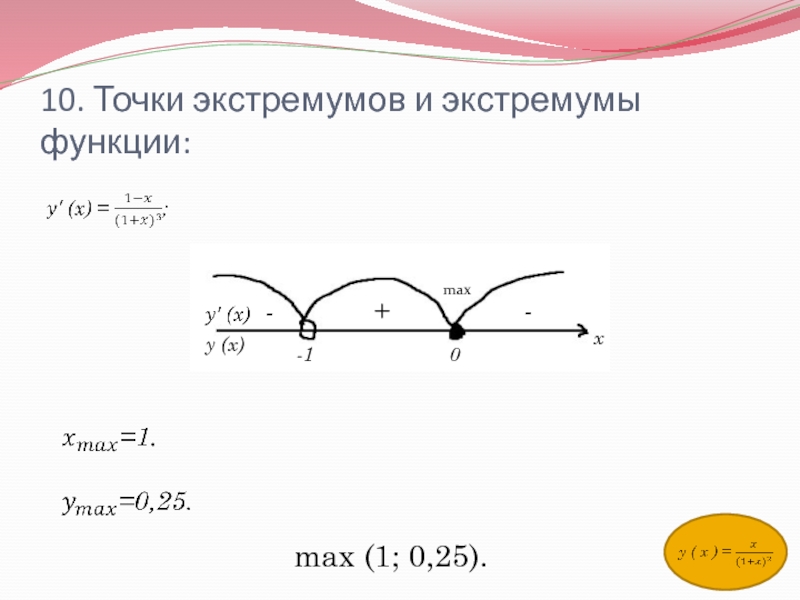
- 11. 10. Точки экстремумов и экстремумы функции:-10+--xy (x)maxmax (1; 0,25).
- 12. 11. Вторая производная функции:
- 13. 12. Критические точки функции (вторая производная):2x-4=0;2x=4;x=2. Стационарная точка 2-й производной.
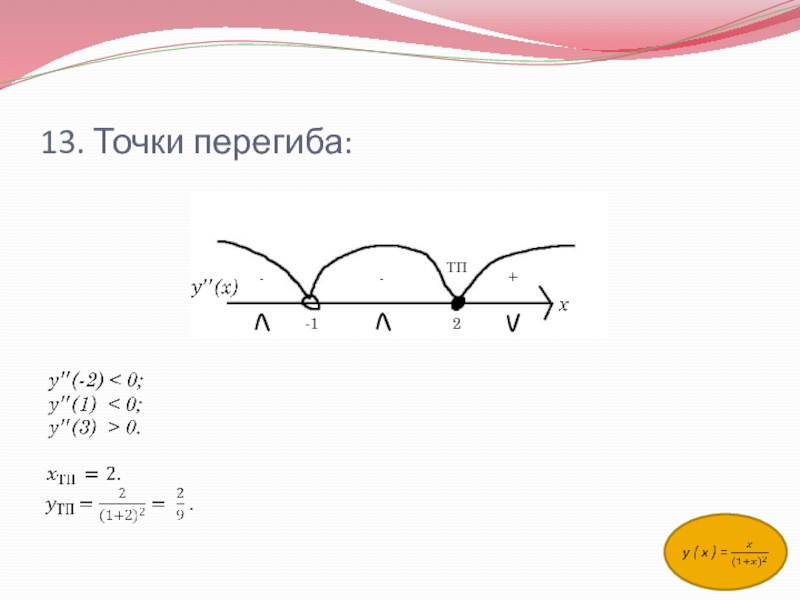
- 14. 13. Точки перегиба:-12--+ТП
- 15. 14. Асимптоты функции (вертикальная, горизонтальная, наклонная):
- 16. 3) Наклонная:Наклонной асимптоты нет (см. слайд 15)
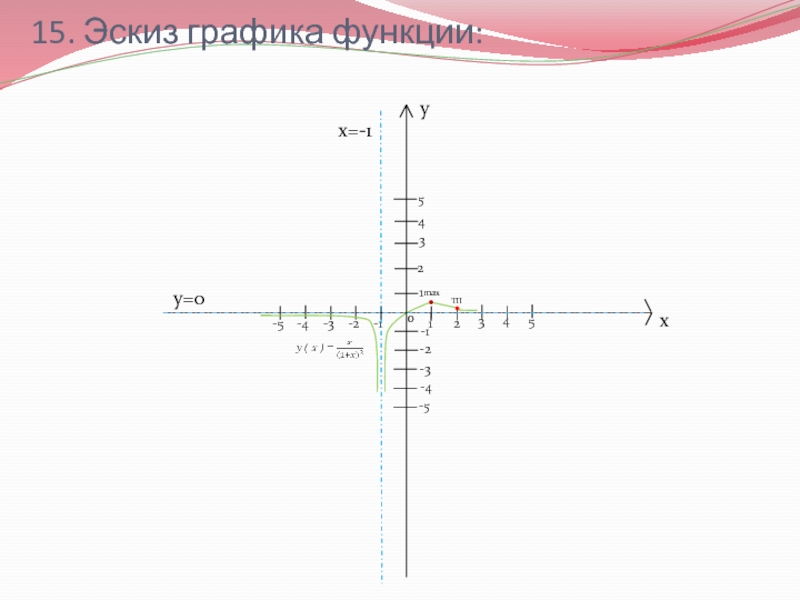
- 17. 15. Эскиз графика функции:xy1324512345-5-4-3-2-1-5-4-3-2-1x=-10maxТПy=0
- 18. Скачать презентанцию
1. Область определения функции:D (y) = (-∞;-1);(-1;+∞).
Слайды и текст этой презентации
Слайд 1Исследование функции с помощью производной
Вариант №6
Презентацию подготовили: Гладышева Анастасия и
Кучинов Даниил
![2. Множество значений функции:E (y) = (-∞;0,25].](/img/thumbs/79703c523424459b7f0c861b545acbe2-800x.jpg "Исследование функции с помощью производной 2. Множество значений функции:E (y) = (-∞;0,25].")
Слайд 43. Исследование на четность:
Т. к. не выполняются равенства
то
это функция общего вида, а значит график функции не симметричен ни оси ординат, ни началу координат.
Слайд 65. Нули функции:
Уравнение имеет корень
, следовательно, график функции пересекает ось OX в точке (0;0).
y
( x ) = 0 x = 0.
Слайд 98. Критические точки функции
(первая производная):
D (y) = (-∞;-1);(-1;+∞)
=> x = -1 –
критическая точка особого вида. 
Слайд 109. Промежутки монотонности функции:
Значит, промежутки монотонности:
-1
1
+
-
-
x
y (x)
(-1; 1];
(-∞; -1);[1; +∞).
![9. Промежутки монотонности функции:Значит, промежутки монотонности:-11+--xy (x)(-1; 1];(-∞; -1);[1; +∞).](/img/thumbs/c348072e9644053e93300b95c18fc486-800x.jpg "Исследование функции с помощью производной 9. Промежутки монотонности функции:Значит, промежутки монотонности:-11+--xy (x)(-1; 1];(-∞; -1);[1; +∞).")
Слайд 1312. Критические точки функции
(вторая производная):
2x-4=0;
2x=4;
x=2. Стационарная точка 2-й производной.
