Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Исследование колебаний маятников различных видов
Содержание
- 1. Исследование колебаний маятников различных видов
- 2. Слайд 2
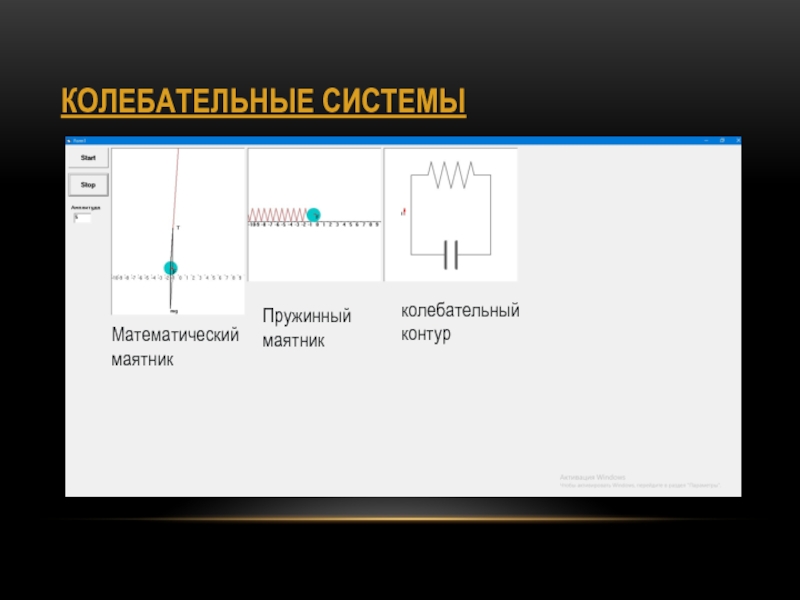
- 3. КОЛЕБАТЕЛЬНЫЕ СИСТЕМЫМатематический маятникколебательный контурПружинный маятник
- 4. КОДОВАЯ СТРАНИЦА
- 5. Слайд 5
- 6. Механические колебания Механические колебания – это движения,
- 7. Пружинный маятникПружинный маятник представляет собой материальную точку
- 8. Математический маятникМатематический маятник представляет собой идеализированную систему в
- 9. Гармонические колебаниеЭто периодическое колебание, при котором координата, скорость, ускорение,
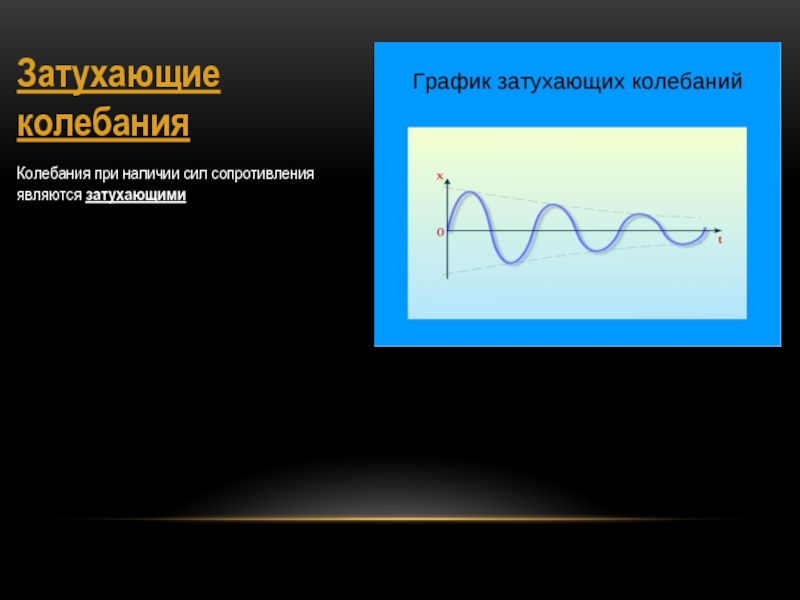
- 10. Затухающие колебанияКолебания при наличии сил сопротивления являются затухающими
- 11. РезонансРезкое возрастание амплитуды вынужденных колебаний при совпадении
- 12. колебательный контурПростейшая система, в которой могу происходить
- 13. Свободные электромагнитные колебания, превращение энергии при электромагнитных
- 14. Аналогия между механическими и электромагнитными колебаниямиЭлектромагнитные колебания
- 15. Аналогия между электрическими и механическими величинами
- 16. Гармонические колебания электрона
- 17. Скачать презентанцию
ЦЕЛИ И ЗАДАЧИНашей главной целью является приобрести навыки в методах работы с колебательными системами, знать, что такое резонанс, как его получить
Слайды и текст этой презентации
Слайд 2
ЦЕЛИ И ЗАДАЧИ
Нашей главной целью является приобрести навыки в методах
работы с колебательными системами, знать, что такое резонанс, как его получить и как его избежать, если он опасен. Мы сравниваем механические и электромагнитные колебания, находим подобия, пытаемся довести до автоматизма наше понимание колебательных явлений.Слайд 6Механические колебания
Механические колебания – это движения, которые точно или приблизительно
повторяются через определённые интервалы времени.
Различают следующие виды механических колебаний:
Свободные или
собственные.Вынужденные
Слайд 7Пружинный маятник
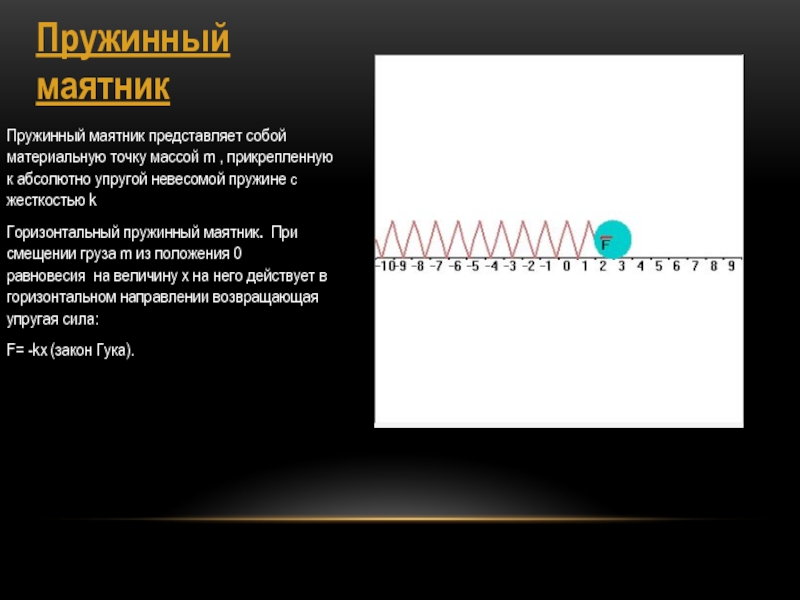
Пружинный маятник представляет собой материальную точку массой m , прикрепленную
к абсолютно упругой невесомой пружине с жесткостью k
Горизонтальный пружинный маятник. При
смещении груза m из положения 0 равновесия на величину x на него действует в горизонтальном направлении возвращающая упругая сила: F= -kx (закон Гука).
Слайд 8Математический маятник
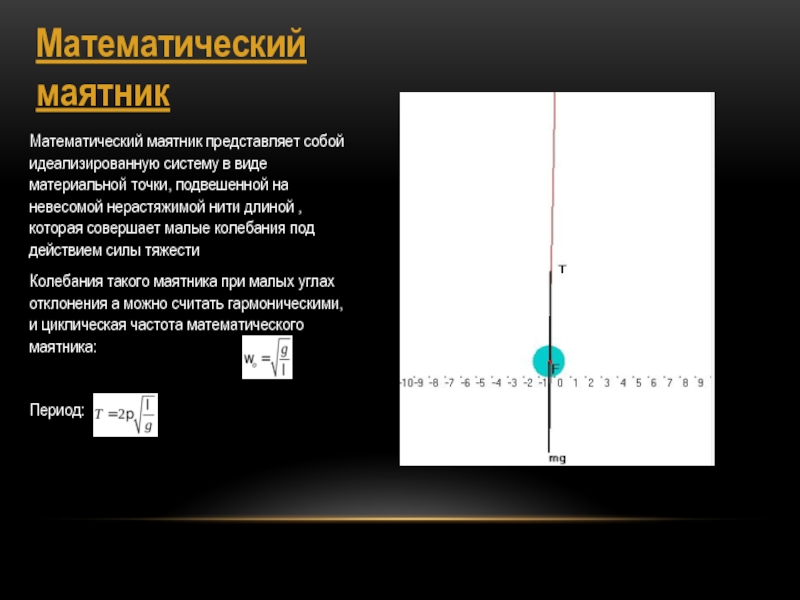
Математический маятник представляет собой идеализированную систему в виде материальной точки,
подвешенной на невесомой нерастяжимой нити длиной , которая совершает малые колебания
под действием силы тяжестиКолебания такого маятника при малых углах отклонения a можно считать гармоническими, и циклическая частота математического маятника:
Период:
Слайд 9Гармонические колебание
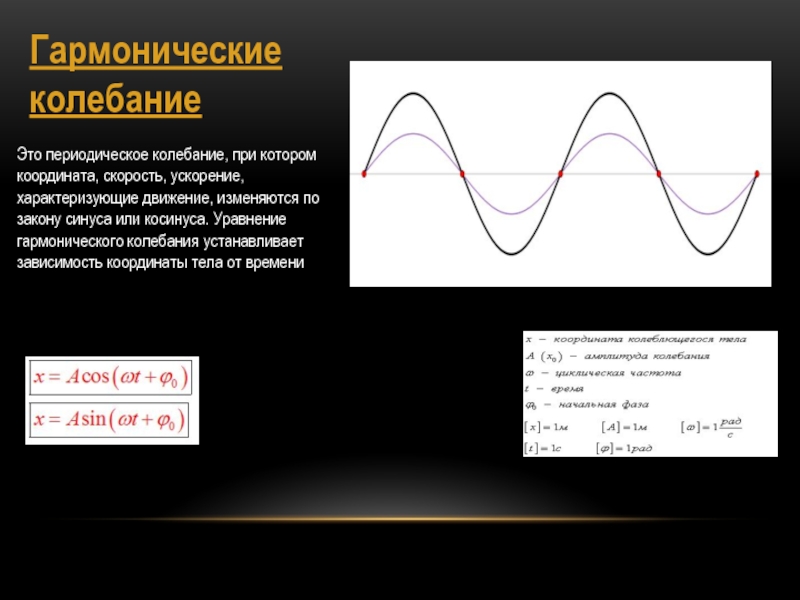
Это периодическое колебание, при котором координата, скорость, ускорение, характеризующие движение, изменяются
по закону синуса или косинуса. Уравнение гармонического колебания устанавливает зависимость
координаты тела от времениСлайд 11Резонанс
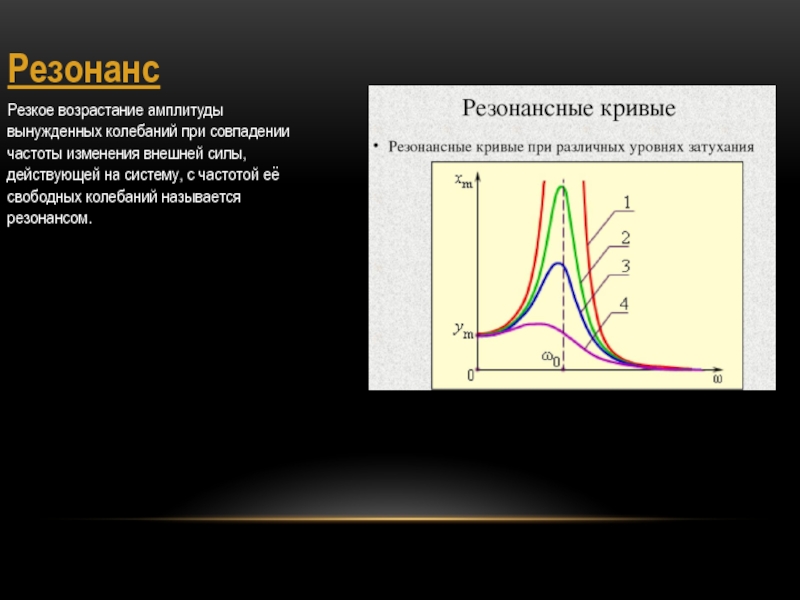
Резкое возрастание амплитуды вынужденных колебаний при совпадении частоты изменения внешней
силы, действующей на систему, c частотой её свободных колебаний называется
резонансом.Слайд 12колебательный контур
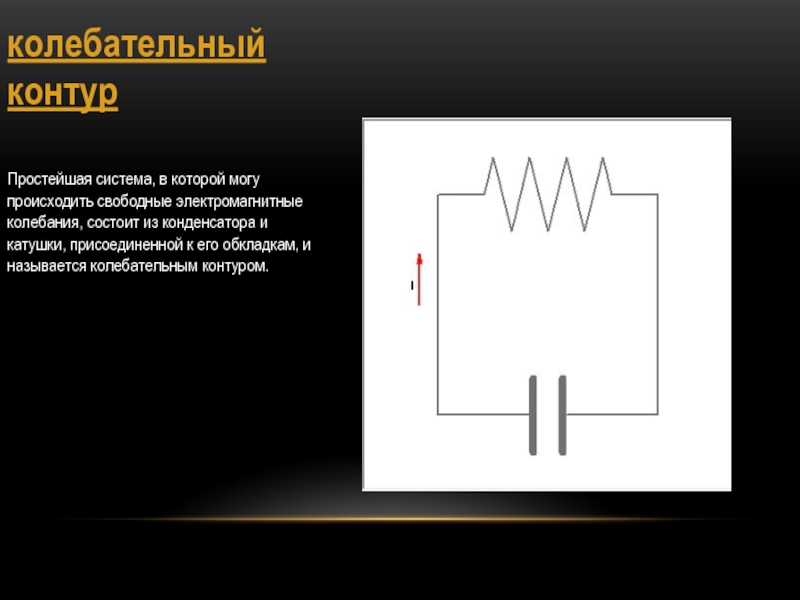
Простейшая система, в которой могу происходить свободные электромагнитные колебания,
состоит из конденсатора и катушки, присоединенной к его обкладкам, и
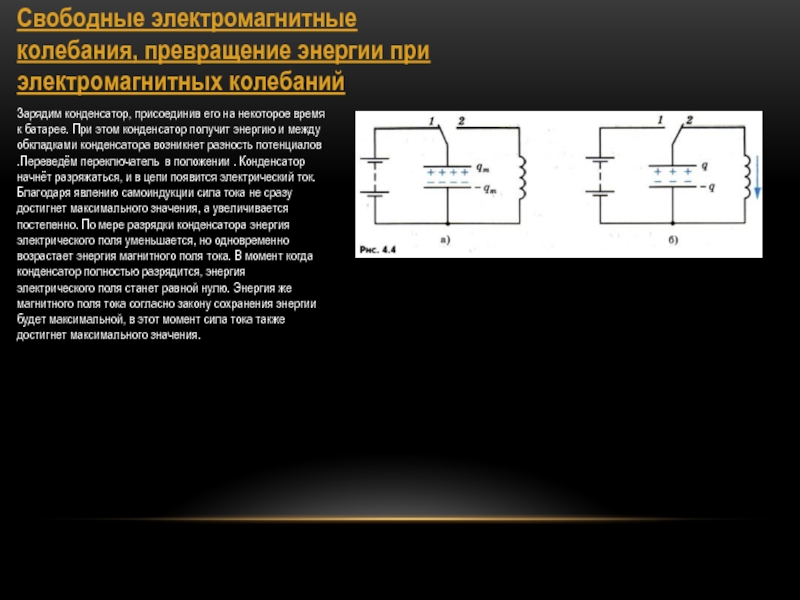
называется колебательным контуром.Слайд 13Свободные электромагнитные колебания, превращение энергии при электромагнитных колебаний
Зарядим конденсатор, присоединив
его на некоторое время к батарее. При этом конденсатор получит
энергию и между обкладками конденсатора возникнет разность потенциалов .Переведём переключатель в положении . Конденсатор начнёт разряжаться, и в цепи появится электрический ток. Благодаря явлению самоиндукции сила тока не сразу достигнет максимального значения, а увеличивается постепенно. По мере разрядки конденсатора энергия электрического поля уменьшается, но одновременно возрастает энергия магнитного поля тока. В момент когда конденсатор полностью разрядится, энергия электрического поля станет равной нулю. Энергия же магнитного поля тока согласно закону сохранения энергии будет максимальной, в этот момент сила тока также достигнет максимального значения.Слайд 14Аналогия между механическими и электромагнитными колебаниями
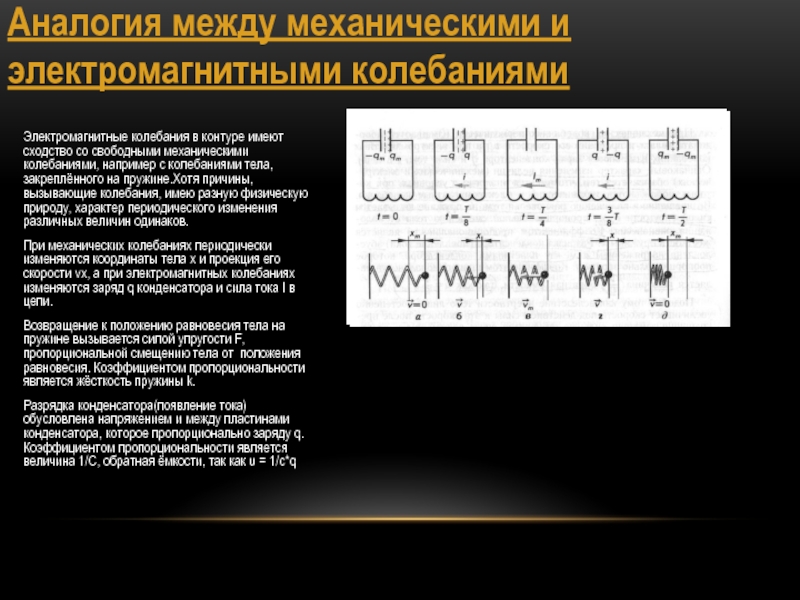
Электромагнитные колебания в контуре имеют
сходство со свободными механическими колебаниями, например с колебаниями тела, закреплённого
на пружине.Хотя причины, вызывающие колебания, имею разную физическую природу, характер периодического изменения различных величин одинаков.При механических колебаниях периодически изменяются координаты тела x и проекция его скорости vx, а при электромагнитных колебаниях изменяются заряд q конденсатора и сила тока I в цепи.
Возвращение к положению равновесия тела на пружине вызывается силой упругости F, пропорциональной смещению тела от положения равновесия. Коэффициентом пропорциональности является жёсткость пружины k.
Разрядка конденсатора(появление тока) обусловлена напряжением и между пластинами конденсатора, которое пропорционально заряду q. Коэффициентом пропорциональности является величина 1/C, обратная ёмкости, так как u = 1/c*q