Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Кафедра Вычислительных машин систем и сетей
Содержание
- 1. Кафедра Вычислительных машин систем и сетей
- 2. ПРИНЦИПЫ РЕАЛИЗАЦИИ МОДУЛЯРНЫХ ВЫЧИСЛЕНИЙ
- 3. ПРИНЦИПЫ РЕАЛИЗАЦИИ МОДУЛЯРНЫХ ВЫЧИСЛЕНИЙ
- 4. ПРИНЦИПЫ РЕАЛИЗАЦИИ МОДУЛЯРНЫХ ВЫЧИСЛЕНИЙ ?
- 5. Слайд 5
- 6. Слайд 6
- 7. Слайд 7
- 8. Слайд 8
- 9. Слайд 9
- 10. Слайд 10
- 11. Слайд 11
- 12. Слайд 12
- 13. Слайд 13
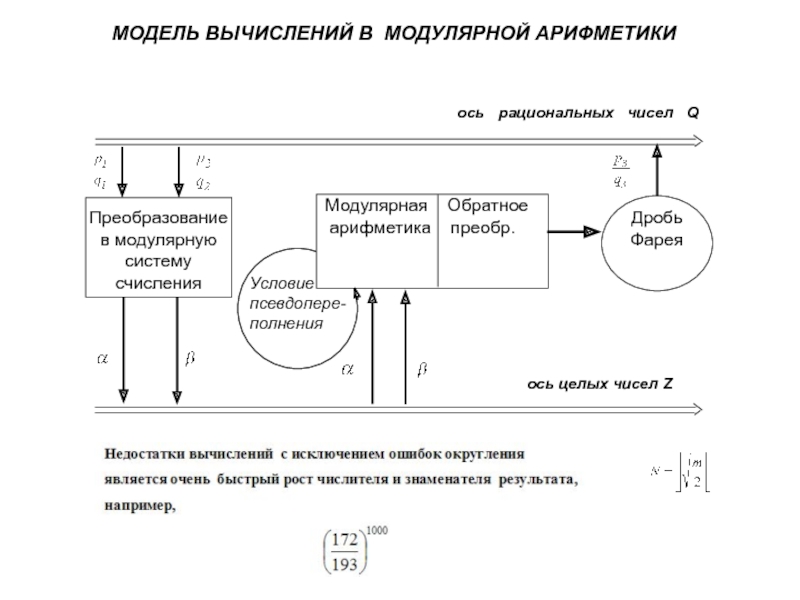
- 14. МОДЕЛЬ ВЫЧИСЛЕНИЙ В МОДУЛЯРНОЙ АРИФМЕТИКИ
- 15. ВОЗМОЖНЫЕ ПРИЛОЖЕНИЯ ВЫЧИСЛЕНИЙ С ИСКЛЮЧЕНИЕМ ОШИБОК ОКРУГЛЕНИЯ1.
- 16. МОДЕЛЬ ВЫЧИСЛЕНИЙ С ИСКЛЮЧЕНИЕМ ОШИБОК ОКРУГЛЕНИЯ НА
- 17. Задача «Котенок ГАВ»
- 18. Слайд 18
- 19. Подход к решению проблемы высокоточных вычислений на
- 20. Оценка эффективности высокоточных вычислений на примере нахождения
- 21. Скачать презентанцию
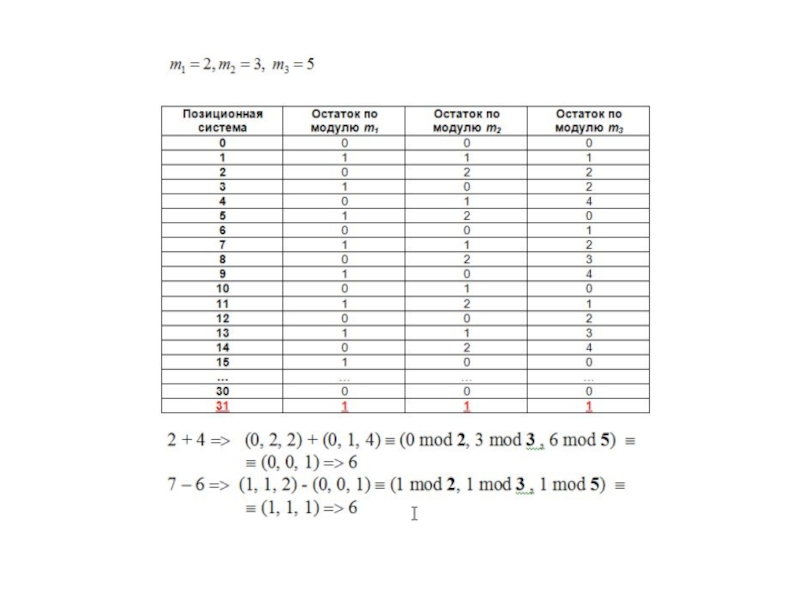
ПРИНЦИПЫ РЕАЛИЗАЦИИ МОДУЛЯРНЫХ ВЫЧИСЛЕНИЙ
Слайды и текст этой презентации
Слайд 1Кафедра Вычислительных машин систем и сетей
Московский энергетический институт
Лекция на тему:
«Модулярная
арифметика»
Слайд 15ВОЗМОЖНЫЕ ПРИЛОЖЕНИЯ ВЫЧИСЛЕНИЙ С ИСКЛЮЧЕНИЕМ ОШИБОК ОКРУГЛЕНИЯ
1. Точное вычисление обобщенных
обратных матриц. Например, таких как, g-обратная матрица Мура-Пенроуза. Многие
алгоритмы требуют умения распознавать значение численного ранга, а это является трудной задачей при наличии ошибок округления.2. Целочисленное решение систем линейных уравнений. Примером могут служить построение оптимальных решений в задачах целочисленного программирования.
3. Точное вычисление характеристического многочлена матрицы. Вследствие ошибок округления будут получены приближенные значения коэффициентов. Если многочлен плохо обусловлен, то корни "приближенного» характеристического уравнения могут быть плохими приближениями к корням истинного уравнения.
4. Обращение матриц Гильберта, Адамара и др. особо чувствительных к ошибкам округления.
5. Для решения промежуточных между классами корректных и некорректных задач.
Класс задач, изменяющих корректность при решении. Это расчет устойчивости систем управления, выч. собств. знач. систем лин. одн. урав. и др.
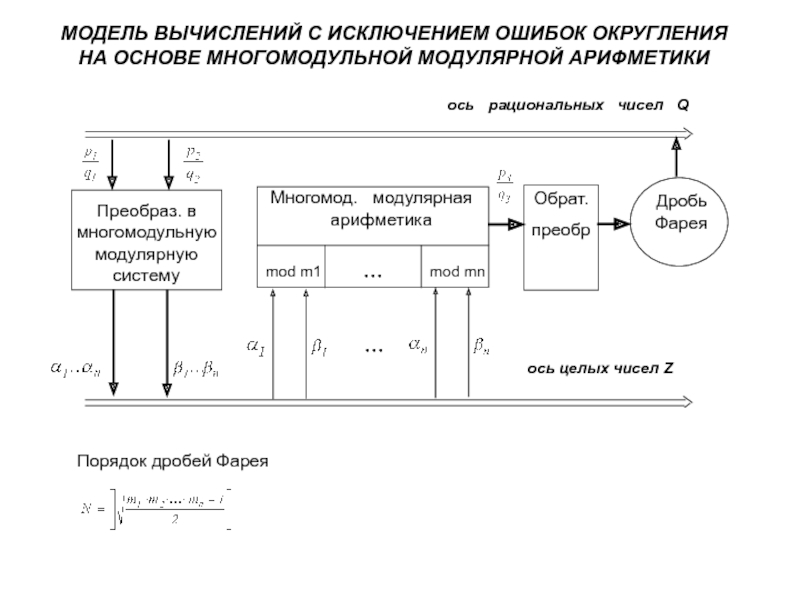
Слайд 16МОДЕЛЬ ВЫЧИСЛЕНИЙ С ИСКЛЮЧЕНИЕМ ОШИБОК ОКРУГЛЕНИЯ НА ОСНОВЕ МНОГОМОДУЛЬНОЙ МОДУЛЯРНОЙ
АРИФМЕТИКИ
ось целых чисел Z
Преобраз. в многомодульную модулярную систему
Дробь
Фарея
Многомод.
модулярная
арифметика mod m1 mod mn
ось рациональных чисел Q
...
...
Обрат.
преобр
Порядок дробей Фарея
Слайд 19Подход к решению проблемы высокоточных вычислений на основе модулярной арифметики
К настоящему времени модулярная арифметика
использовалась как средство повышения быстродействия в криптографии, нейронных сетях, цифровой обработке сигналов и др.Проведенные исследования показали качественно новые возможности применения модулярной арифметики в повышении точности вычислений и ослаблении зависимости времени вычислений от точности, для некоторых частных задач:
решение дифференциальных уравнений методами Рунге-Кутта,
нахождение скалярного произведения векторов,
решения систем линейных уравнений методами Гаусса-Зейделя,
релаксации,
дискретном преобразовании Фурье .
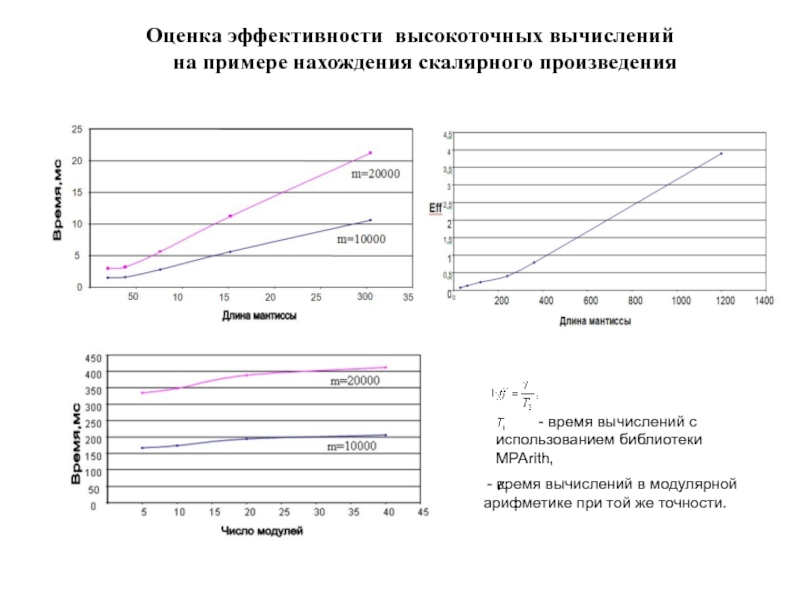
Слайд 20Оценка эффективности высокоточных вычислений на примере нахождения скалярного произведения
-
время вычислений с использованием библиотеки MPArith,
- время вычислений в
модулярной арифметике при той же точности.