Разделы презентаций

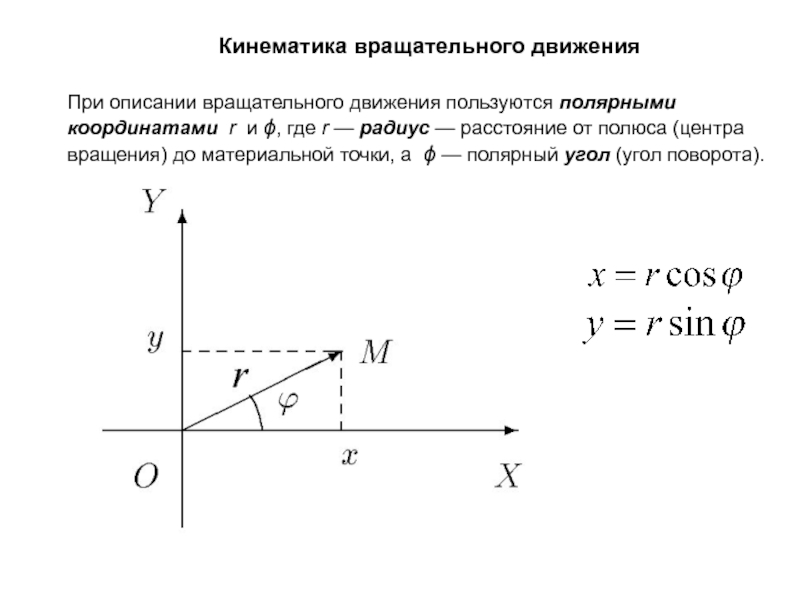
Кинематика вращательного движения При описании вращательного движения

Содержание

Элементарные повороты d можно рассматривать как псевдовекторы.Угловое перемещение d — векторная величина, модуль которой равен углу поворота, а направление совпадает с направлением поступательного движения правого винта.Угловая скорость: Вектор  направлен вдоль

Слайды и текст этой презентации

Слайд 1Кинематика вращательного движения
При описании вращательного движения пользуются полярными координатами

r и , где r — радиус — расстояние от

полюса (центра вращения) до материальной точки, а  — полярный угол (угол поворота).
Кинематика вращательного движения При описании вращательного движения пользуются полярными координатами r и , где r — радиус

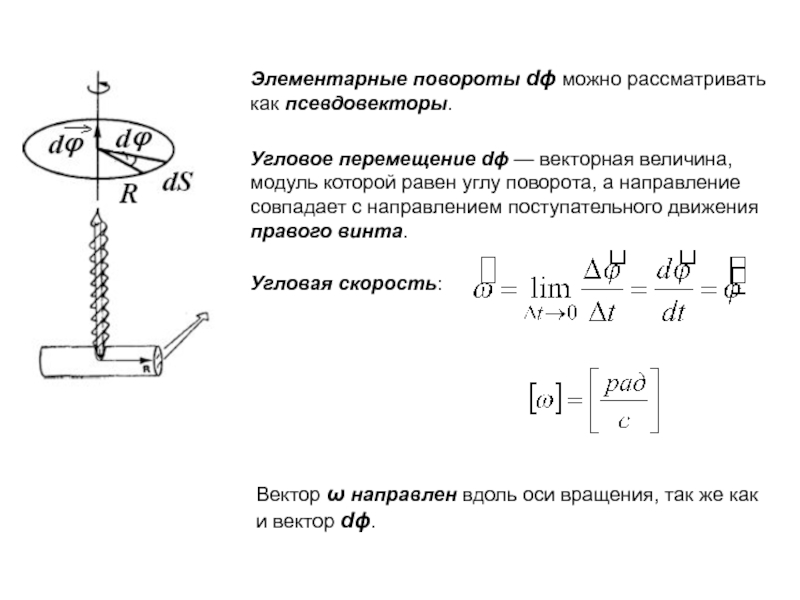
Слайд 2Элементарные повороты d можно рассматривать как псевдовекторы.
Угловое перемещение d —

векторная величина, модуль которой равен углу поворота, а направление совпадает

с направлением поступательного движения правого винта.

Угловая скорость:

Вектор  направлен вдоль оси вращения, так же как и вектор d.

Элементарные повороты d можно рассматривать как псевдовекторы.Угловое перемещение d — векторная величина, модуль которой равен углу поворота,

Слайд 3Зависимость угла поворота от времени при равномерном вращении
При равномерном вращении:



Проинтегрируем по времени:


Равномерное вращение можно характеризовать периодом вращения — T

временем, за которое точка совершает один полный оборот, 2=T, следовательно

Частота вращения — число полных оборотов, совершаемых телом при равномерном его движении по окружности, в единицу времени:

Единица частоты вращения — герц (Гц)

Зависимость угла поворота от времени при равномерном вращенииПри равномерном вращении: Проинтегрируем по времени:Равномерное вращение можно характеризовать периодом

Слайд 4Связь между линейной и угловой скоростью:

Связь между линейной и угловой скоростью:

Слайд 5Векторное произведение

Векторное произведение

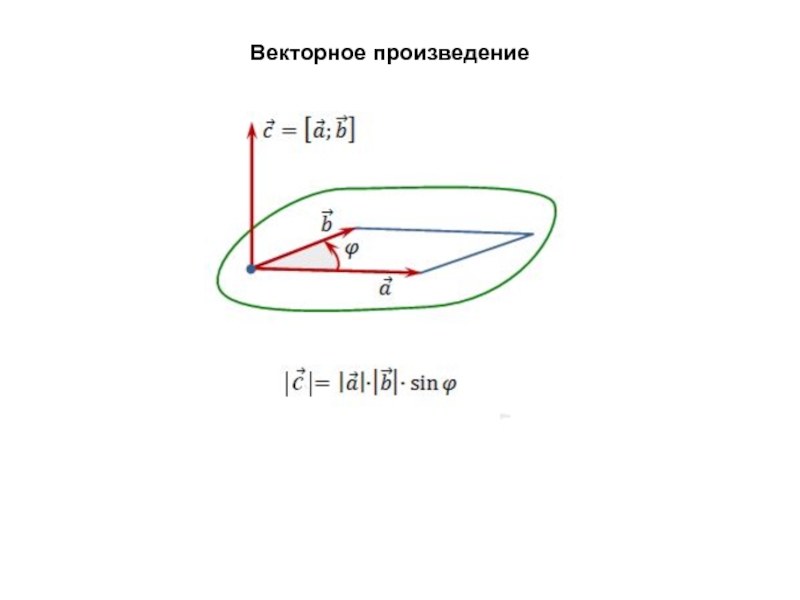
Слайд 6В векторном виде формулу для линейной скорости можно написать как

векторное произведение:
По определению векторного произведения его модуль равен
-угол между

векторами  и R, а направление совпадает с направлением поступательного движения правого винта при его вращении от  к R.
В векторном виде формулу для линейной скорости можно написать как векторное произведение:По определению векторного произведения его модуль

Слайд 7Угловое ускорение:
Вектор  направлен вдоль оси вращения в сторону

вектора приращения угловой скорости d (при ускоренном вращении вектор 

сонаправлен вектору , при замедленном — противонаправлен ему).

Зависимость угловой скорости и угла поворота от времени при равнопеременном вращательном движении

При равнопеременном вращательном движении  =const


проинтегрируем это выражение



Угловое ускорение: Вектор  направлен вдоль оси вращения в сторону вектора приращения угловой скорости d (при ускоренном

Слайд 8Зависимость величины угла поворота от времени получается, если проинтегрировать зависимость

угловой скорости от времени

Выражение для нормальное ускорения имеет вид:
Выражение

для тангенциального ускорения -

Связь пути и величины углового перемещения выглядит следующим образом:

Зависимость величины угла поворота от времени получается, если проинтегрировать зависимость угловой скорости от времени Выражение для нормальное

Слайд 9Величина полного ускорения

Величина полного ускорения

Похожие презентации

Гормондар биохимиясы Гормондар биохимиясы 864
Горбач Евгений. Группа 1217 Горбач Евгений. Группа 1217 216
7 Солнечный свет на Земле д\з §7 Вопросы 1-9 стр. 28 7 Солнечный свет на Земле д\з §7 Вопросы 1-9 стр. 28 444
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ ФГАОУ ВПО УРАЛЬСКИЙ МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ ФГАОУ ВПО УРАЛЬСКИЙ 208
Маркетинг без бюджета Маркетинг без бюджета 283
Тема 10: Развитие личности и её жизненный путь Тема 10: Развитие личности и её жизненный путь 270
Лекция № 9 Лекция № 9 210
Синдром Клайнфельтера Синдром Клайнфельтера 520
Занятие 1. Базовая модель макроэкономического равновесия Занятие 1. Базовая модель макроэкономического равновесия 246
Состояние оказания помощи взрослым пациентам с гемофилией в Республике Беларусь Состояние оказания помощи взрослым пациентам с гемофилией в Республике Беларусь 185
Презентация непосредственно образовательной деятельности по формированию Презентация непосредственно образовательной деятельности по формированию 264
внедрение единой платежной системы для жилищно-коммунального хозяйства на внедрение единой платежной системы для жилищно-коммунального хозяйства на 193
Катионы IV (Al 3+, Cr 3+, Zn 2+, Sn 2+, Sn (IV), As (III), As Катионы IV (Al 3+, Cr 3+, Zn 2+, Sn 2+, Sn (IV), As (III), As 325
Chapter 2 The Financial Market Environment Chapter 2 The Financial Market Environment 228
Coral DRAW Coral DRAW 224
Управление муниципальным хозяйством Управление муниципальным хозяйством 294
Тема: Философия Нового времени Лекция №2: Проблемы гносеологии Тема: Философия Нового времени Лекция №2: Проблемы гносеологии 429
Озёра Озёра 295
Absurdity in English and Russian literature Absurdity in English and Russian literature 226
Отцы и дети Отцы и дети 204

Обратная связь

Если не удалось найти и скачать доклад-презентацию, Вы можете заказать его на нашем сайте. Мы постараемся найти нужный Вам материал и отправим по электронной почте. Не стесняйтесь обращаться к нам, если у вас возникли вопросы или пожелания:

Email: Нажмите что бы посмотреть 

Что такое TheSlide.ru?

Это сайт презентации, докладов, проектов в PowerPoint. Здесь удобно  хранить и делиться своими презентациями с другими пользователями.

Для правообладателей

Яндекс.Метрика