Кинетические свойства радиоматериалов

устанавливающая свойства симметрии кинетических коэффициентов. Доказана Л. Онсагером в 1931.
КИНЕТИЧЕСКИЕ

КОЭФФИЦИЕНТЫ Lik определяют как коэффициенты в линейных соотношениях между силами Xk  (градиентами температуры Т, электрического потенциала и  концентрации) и потоками   Ji :                                              

Пусть на кристалл
действуют:

СПбГЭТУ «ЛЭТИ», кафедра МИТ, ОЭиР, 2013

собой газ, состоящий из частиц с массой m* , движущихся

на фоне тяжелых неподвижных ионов, к которому применима кинетическая теория идеальных газов.

СПбГЭТУ «ЛЭТИ», кафедра МИТ, ОЭиР, 2013

металле
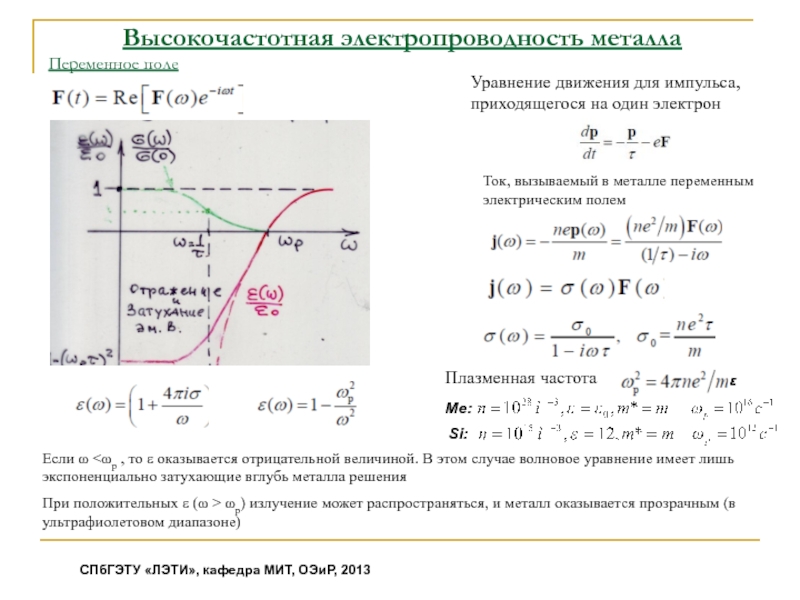
может быть большой и определяется энергией Ферми)

плотность тока:
                                     
Закон Ома:

                                                              

подвижность:

                                          
тепловая энергия электрона:
                              

Недостатки теории Друде
Средняя длина свободного пробегаСредняя длина свободного пробега электрона оказывается на несколько порядков больше, чем шаг кристаллической решёткиСредняя длина свободного пробега электрона оказывается на несколько порядков больше, чем шаг кристаллической решётки. Объяснение этому даётся в квантовой теорииСредняя длина свободного пробега электрона оказывается на несколько порядков больше, чем шаг кристаллической решётки. Объяснение этому даётся в квантовой теории, где показывается, что в идеальном кристаллеСредняя длина свободного пробега электрона оказывается на несколько порядков больше, чем шаг кристаллической решётки. Объяснение этому даётся в квантовой теории, где показывается, что в идеальном кристалле при нулевой температуреСредняя длина свободного пробега электрона оказывается на несколько порядков больше, чем шаг кристаллической решётки. Объяснение этому даётся в квантовой теории, где показывается, что в идеальном кристалле при нулевой температуре электрон не рассеивается вообще, но в реальном кристалле он рассеивается на примесяхСредняя длина свободного пробега электрона оказывается на несколько порядков больше, чем шаг кристаллической решётки. Объяснение этому даётся в квантовой теории, где показывается, что в идеальном кристалле при нулевой температуре электрон не рассеивается вообще, но в реальном кристалле он рассеивается на примесях, дефектахСредняя длина свободного пробега электрона оказывается на несколько порядков больше, чем шаг кристаллической решётки. Объяснение этому даётся в квантовой теории, где показывается, что в идеальном кристалле при нулевой температуре электрон не рассеивается вообще, но в реальном кристалле он рассеивается на примесях, дефектах и фононах, возмущениях кристаллической решетки.

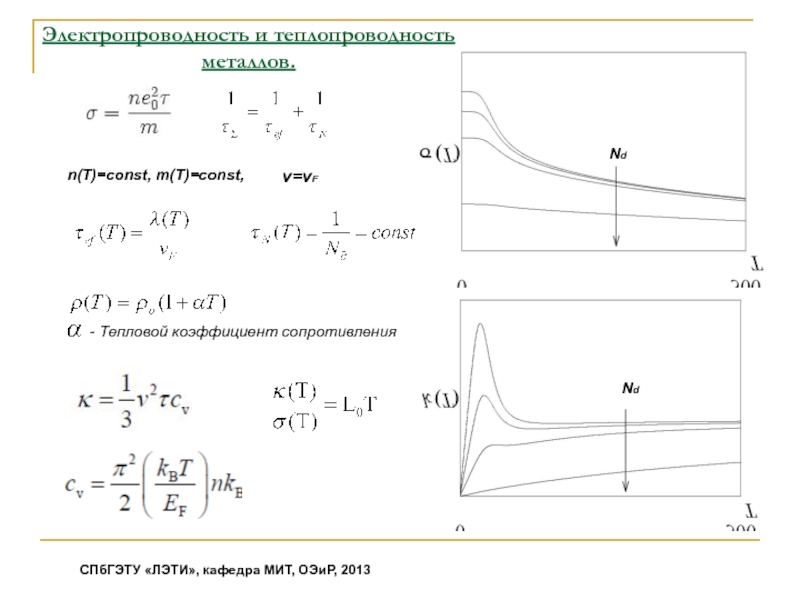
    -электрическая удельная проводимость
 - концентрация электронов
 - элементарный заряд
 - время релаксации по импульсам
 (время, за которое электрон «забывает»
о том в какую сторону двигался)
 - эффективная масса электрона
- теплопроводность
v - тепловая скорость

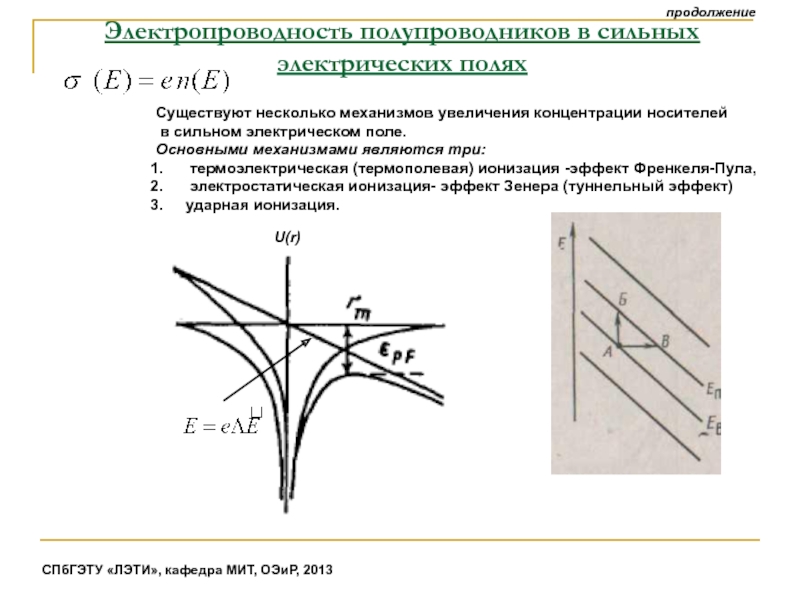
продолжение

СПбГЭТУ «ЛЭТИ», кафедра МИТ, ОЭиР, 2013

немецкими учёными Г. Видеманом (1826—1899) и Р. Францем (1827—1902) на основании экспериментальных данных было

установлено, что для различных металлов при одинаковой температуре отношение              практически не изменяется.
Пропорциональность этого отношения термодинамической температуре была установлена 
Л. Лоренцем в 1882 г. В его честь коэффициент      носит название числа Лоренца.
Взаимная связь электрической проводимости и теплопроводности объясняется тем, что оба эти свойства металлов в основном обусловлены движением свободных электронов.
Коэффициент теплопроводности увеличивается пропорционально средней скорости частиц, так как ускоряется перенос энергии. Электропроводность, наоборот, падает, потому что соударения при большой скорости частиц значительно затрудняют перенос энергии .

СПбГЭТУ «ЛЭТИ», кафедра МИТ, ОЭиР, 2013

(1)

(2)

теле (материале) несколько рассеивающих центров, то по правилу нахождения вероятности

сложного события, вероятность столкновения носителя (рассеяния)
заряда с рассеивающими центрами и результирующее время релаксации определяется:

Электропроводность металлов. (модель Зоммерфельда)

СПбГЭТУ «ЛЭТИ», кафедра МИТ, ОЭиР, 2013

следующими соотношениями Блоха-Грюнайзена:




Электропроводность металлов.
Процессы рассеяния электронов в металлах можно подразделить

на два вида:
рассеяние электронов на фононах (тепловых колебаниях решетки)
рассеяние электронов на дефектах структуры (нейтральных).

Рассеяние электронов на фононах по-разному зависит от температуры.

СПбГЭТУ «ЛЭТИ», кафедра МИТ, ОЭиР, 2013

кафедра МИТ, ОЭиР, 2013

со средней длиной свободного пробега,
границы пленки накладывают ограничение на

движение электронов проводимости.
Возникающие при этом физические эффекты называются классическими размерными эффектами.

Различают зеркальное и диффузное отражение электронов от границ поверхности.
Коэффициент зеркальности p зависит от шероховатости поверхности и
определяется отношением зеркально отраженных электронов к полному числу электронов, падающих на поверхность.

Электропроводность тонкой пленки как функция толщины d определяется интегральным выражением (по теории Фукса)

где: γ =d / λ,беск, λ,беск - средняя длина свободного пробега бесконечно толстого образца,
a - параметр, определяемый углом отражения электронов от границ поверхности.

СПбГЭТУ «ЛЭТИ», кафедра МИТ, ОЭиР, 2013

импульса,
приходящегося на один электрон
Плазменная частота
Если ω

ε оказывается отрицательной величиной. В этом случае волновое уравнение имеет лишь экспоненциально затухающие вглубь металла решения
При положительных ε (ω > ωp) излучение может распространяться, и металл оказывается прозрачным (в ультрафиолетовом диапазоне)

Высокочастотная электропроводность металла

Ме:

СПбГЭТУ «ЛЭТИ», кафедра МИТ, ОЭиР, 2013

в собственном невырожденном полупроводнике определяются
выражениями:




СПбГЭТУ «ЛЭТИ», кафедра МИТ, ОЭиР,

2013

2013

где tp - время жизни дырок; 
tn - время жизни электронов
Время жизни избыточных

носителей составляет 0,01...0,001 с.

Соотношения Эйнштейна:

СПбГЭТУ «ЛЭТИ», кафедра МИТ, ОЭиР, 2013

2013
Эффект Френкеля-Пула, эффект Зенера
Поля, у которых напряженность меньше критического 
значения, называют

слабыми,
больше критического — сильными

Сильное электрическое поле влияет на подвижность и концентрацию носителей заряда.

Если электропроводность с ростом поля увеличивается, то BAX наз. Суперлинейной (3), если же падает,- сублинейной(2).

Основными механизмами являются три:
термоэлектрическая (термополевая) ионизация -эффект Френкеля-Пула,
электростатическая

ионизация- эффект Зенера (туннельный эффект)
ударная ионизация. 

Электропроводность полупроводников в сильных электрических полях

продолжение

СПбГЭТУ «ЛЭТИ», кафедра МИТ, ОЭиР, 2013

3 кВ/см, для ІпР — около 6 кВ/см.
m*2 = 1,2

m0 

J = e (m*1 n1+m *2 n2)

на участке E1< E< E2 должны наблюдаться уменьшение средней дрейфовой скорости и спад плотности тока при росте напряженности внешнего поля (отрицательная дифференциальная подвижность и отрицательное дифференциальное сопротивление)

движение “горячих” и “холодных” электронов приводит к формированию подвижного двойного электрического слоя зарядов - домена

Если к образцу полупроводника приложить электрическое поле с напря­женностью, большей некоторого порогового значения, то в таком образце могут возникнуть высокочастотные колебания электриче­ского тока.

СПбГЭТУ «ЛЭТИ», кафедра МИТ, ОЭиР, 2013

проводимость которой подчиняется закону Ома; б) участок образца внутри домена

обладает отрицательным дифференциальным
сопротивлением, что позволяет использовать образцы в качестве активных элементов усилителей и генераторов СВЧ

продолжение

Эффект Ганна

Образование домена в кристалле соответствует резкому возрастанию удельного сопротивления.
В случае приложения к кристаллу электрического поля с критическим значением напряженности
образование домена приводит к уменьшению тока, проходящего через образец.

На основе эффекта Ганна разработаны диоды Ганна, способные работать на частотах от долей герца до сотен гигагерц. При определенных условиях диод Ганна может работать в режиме ограниченного накопления объемного заряда (ОНОЗ). Максимальная частота колебаний в ОНОЗ теоретически может достигать тысячи гигагерц. В диоде Ганна наблюдают световое излу­чение, лазерный эффект, модуляцию светового потока доменом генерацию мощных ультразвуковых колебаний.

СПбГЭТУ «ЛЭТИ», кафедра МИТ, ОЭиР, 2013

определяется механизмом рассеяния
1. При рассеянии на тепловых колебаниях решетки,

с ростом напряженности поля выше критического значения,
подвижность носителей заряда будет зависеть от напряженности, уменьшаясь с ее ростом по закону Е~1/2.  Скорость носителей заряда определяется энергией. приобретаемой электронами в электричеcком поле:

скорость пропорциональна , следовательно, µ=Е(-|/2)_.

2. При рассеянии на ионизированных примесях подвижность носителей заряда пропорциональна третьей степени скорости. подвижность носителей возрастает,

В области низких температур в сильных электрических полях действуют оба механизма рассеяния, и график зависимости подвиж­ности носителей заряда от напряженности приложенного электри­ческого поля имеет вид, показанный на рис. 5.1.

СПбГЭТУ «ЛЭТИ», кафедра МИТ, ОЭиР, 2013

пер. с англ., M., 1970; Денис В., Пожела Ю., Горячие

электроны, Вильнюс, 1971;
Бонч-Бруевич В. Л., Калашников С. Г., Физикаполупроводников, M., 1977. Ш. M. Коган.

Эффект разогрева электронно-дырочного газа. Электронная температура.

СПбГЭТУ «ЛЭТИ», кафедра МИТ, ОЭиР, 2013