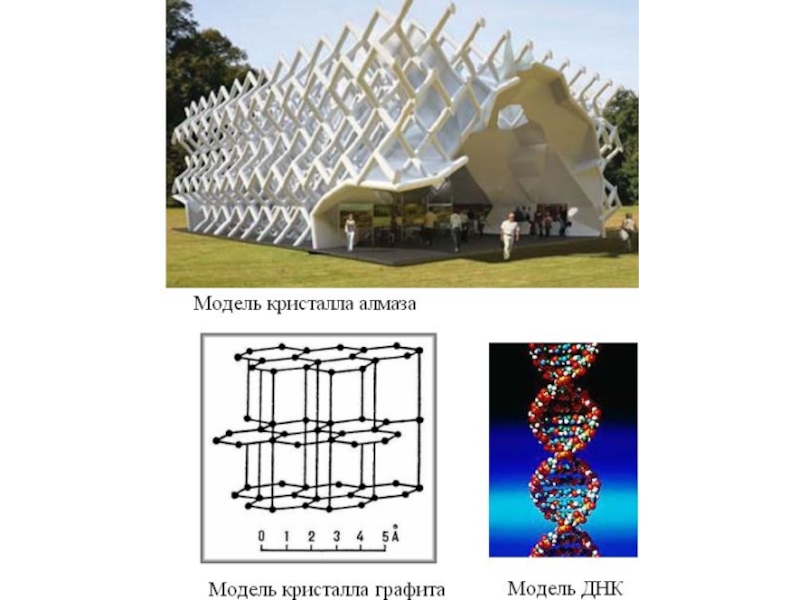
Слайд 1КЛАССИФИКАЦИЯ МОДЕЛЕЙ
Физические (материальные)
Представляют собой технические устройства,
реализованные в материальном виде:
установки;
приборы;
макеты;
тренажеры;
Электрические и электронные блоки, имитирующие работу объекта
Символьные
(абстрактные)
Представляющие собой совокупность символов и правил манипулирования этими символами (грамматика):
формулы;
графики;
таблицы;
тексты;
ноты;
тексты;
схемы (электрические, пневматические, гидравлические).
Слайд 2ФИЗИЧЕСКИЕ МОДЕЛИ
1. Натурные (натуральные) – это практически полные копии
реальных систем или их частей (элементов, подсистем), эксперименты с которыми
обеспечивают наивысший уровень достоверности информации.
2. Масштабные модели – это устройства, установки, в которых реализуются процессы той же физической природы, что и в оригинале, но в иных (чаще всего, в меньших) масштабах.
3. Аналоговые модели принципиально отличаются от натурных и масштабных моделей тем, что процессы исходной системы изучаются на процессе-аналоге совсем другой физической природы. При этом обязательным условием такого моделирования является физическое подобие процессов.
Под физическим подобием понимается однозначное соответствие между параметрами изучаемого объекта-оригинала и его модели, что выражается в тождественности (или близости) математических описаний процессов, протекающих в них.
Слайд 6ФИЗИЧЕСКИЕ МОДЕЛИ
Применение НАТУРНЫХ МОДЕЛЕЙ оправдано в следующих случаях:
- когда натурное
моделирование проще и обходится дешевле, чем создание каких-то других моделей;
-
когда реальная система уже создана, и по ней необходимо уточнить какие-то характеристики, настроить параметры;
когда необходимую точность, достоверность информации нельзя обеспечить на других, более абстрактных моделях.
ПРИМЕР ФИЗИЧЕСКОГО ПОДОБИЯ ПРОЦЕССОВ:
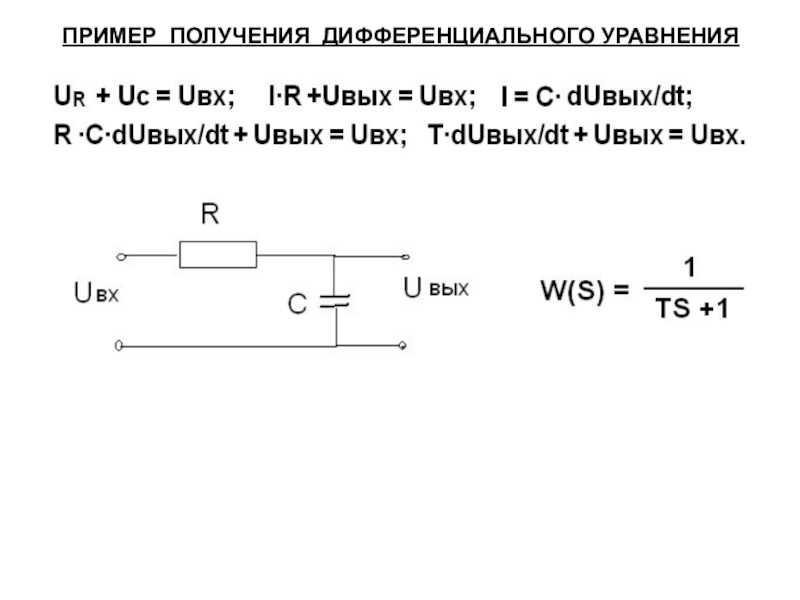
зависимость напряжения U(t) на емкости C от величины тока I(t) может быть представлена уравнением
.
(1)
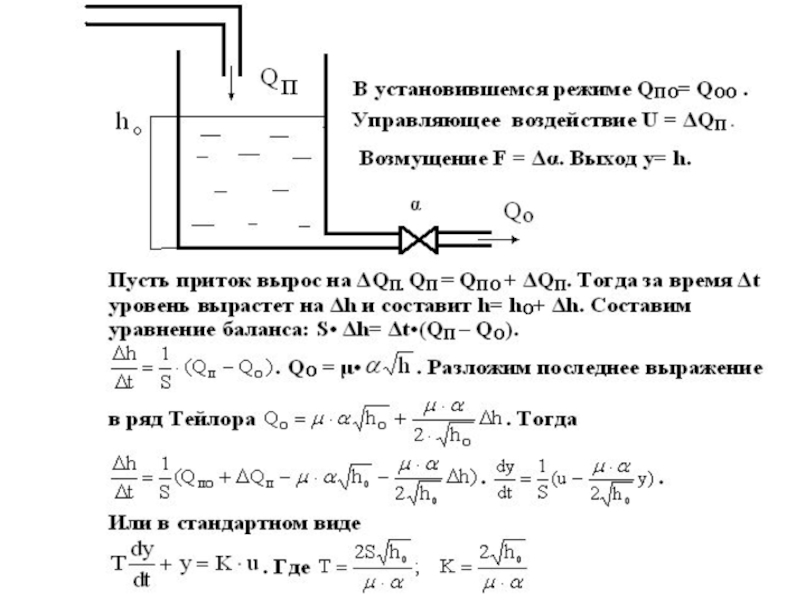
Зависимость уровня жидкости H(t) в цилиндре от расхода жидкости G(t) в цилиндр можно описать уравнением вида
,
(2)
Слайд 7МАТЕМАТИЧЕСКИЕ МОДЕЛИ
Математическая модель представляет собой систему математических соотношений, описывающих изучаемый
процесс или явление. Для составления математической модели могут быть использованы
языки различных разделов математики:
Y= 2X+4
T·dy/dt +y = -5x
A=B∩C
A= lim x(t)
t→∞
Слайд 8КЛАССИФИКАЦИЯ МАТЕМАТИЧЕСКИХ МОДЕЛЕЙ
1.По методу их исследования: аналитические; имитационные.
2. По учету
случайного характера воздействий, связей, изменения параметров:
- детерминированные; стохастические.
3. По
учету переходных процессов в моделируемом объекте:
- статические; динамические.
4. По характеру изменения модельного времени:
- непрерывные; дискретные.
5. По линейности математических соотношений:
- линейные; нелинейные.
Слайд 9Преимущества математических моделей перед физическими
позволяют с помощью набора типовых моделей
решать достаточно широкий класс задач моделирования различных объектов, имеющих похожее
математическое описание;
обеспечивают простоту перехода от одной задачи к другой, изменения начальных условий, внешних воздействий, параметров объекта;
дают возможность моделировать объект по частям, разбивая сложный процесс на элементарные подпроцессы, что особенно существенно при исследовании сложных технологических объектов;
эффективно используют быстродействующие ЭВМ как в процессе проведения экспериментов с моделью, так и при обработке экспериментальных данных;
значительно экономичнее метода физического моделирования как по затратам времени, так и по стоимости моделирования.
Слайд 10ЦЕЛИ МОДЕЛИРОВАНИЯ В ЗАДАЧАХ УПРАВЛЕНИЯ ТЕХНОЛОГИЧЕСКИМИ ОБЪЕКТАМИ
определение оптимального технологического режима
для отдельного технологического агрегата, участка и производства;
оптимальное распределение потоков между
параллельно работающими агрегатами;
выбор структуры регулятора технологического параметра;
оптимизация настроек регулятора;
диагностика причин нарушения технологического регламента;
прогнозирование и предупреждение аварийных ситуаций;
реализация адаптивных систем управления.
Слайд 11ЦЕЛИ МОДЕЛИРОВАНИЯ В ЗАДАЧАХ УПРАВЛЕНИЯ ОРГАНИЗАЦИОННО-ЭКОНОМИЧЕСКИМИ ОБЪЕКТАМИ
определение оптимального плана производства;
выбор
оптимальных объемов запасов сырья, материалов и полуфабрикатов;
прогнозирование изменения спроса рынка
на производимую продукцию;
обоснованное выделение лимитов на энергоресурсы для подразделений предприятия.
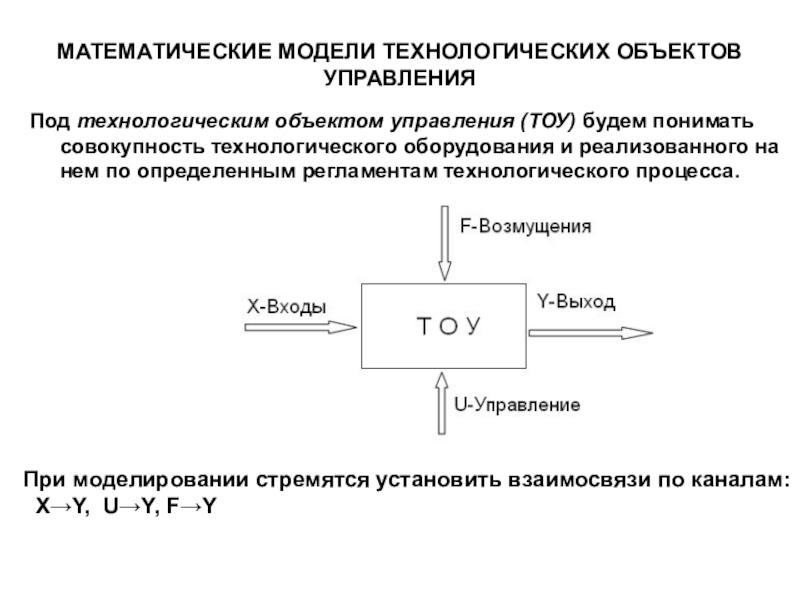
Слайд 12МАТЕМАТИЧЕСКИЕ МОДЕЛИ ТЕХНОЛОГИЧЕСКИХ ОБЪЕКТОВ УПРАВЛЕНИЯ
Под технологическим объектом управления (ТОУ) будем
понимать совокупность технологического оборудования и реализованного на нем по определенным
регламентам технологического процесса.
При моделировании стремятся установить взаимосвязи по каналам:
XY, UY, FY
Слайд 13КАТЕГОРИИ ТОУ ПО ХАРАКТЕРУ ФИЗИКО-ХИМИЧЕСКИХ ПРОЦЕССОВ
гидродинамические процессы (перемещение жидкостей и
газов по трубопроводам и внутри аппаратов, перемешивание в жидкой среде,
очистка газа от пыли и тумана и т.п.). При построении моделей используются законы механики и гидродинамики;
тепловые процессы (процессы нагрева и охлаждения, выпаривания и конденсации, теплообмена). Используются законы термодинамики;
механические процессы (измельчение, грохочение, гранулирование, перемешивание и транспортировка сыпучих материалов). В основу моделей закладываются законы механики;
электромеханические (электродвигатели с электроприводом, генераторы). Используются законы механики и электротехники;
диффузионные (массообменные процессы, связанные с переносом вещества в различных агрегатных состояниях из одной фазы в другую) (дистилляция и ректификация, растворение и кристаллизация, увлажнение и сушка). Используются законы массопереноса.
Слайд 14Формы математических моделей динамических объектов
Дифференциальное уравнение
Физический смысл дифференциального уравнения,
моделирующего реальное инерционное звено, заключается в том, что оно отражает
один из фундаментальных законов природы, определяющий процессы в моделируемом звене. К таким законам относятся:
закон сохранения энергии;
закон сохранения вещества;
закон сохранения количества теплоты;
закон равновесия сил и т.п.
Дифференциальное уравнение имеет балансный характер. В правую часть уравнения записываются действующие на звено силы (или приход энергии, вещества), выраженные через входную величину звена и ее производные. В левую часть – силы сопротивления (или накопление и расход энергии, вещества), выраженные через выходную величину и ее производные.
Общий порядок построения дифференциального уравнения, моделирующего какое-либо звено, заключается в следующем:
Определяются входная и выходная величины звена.
Устанавливается закон (законы), в соответствии с которым протекают основные процессы в звене.
Внешняя сила, энергия, входящий поток вещества выражаются через входную величину звена и ее производные и записываются в правую часть уравнения, а силы сопротивления, накопление и расход энергии или вещества, выраженные через выходную величину и ее производные – в левую часть.

Слайд 15ПРИМЕР ПОЛУЧЕНИЯ ДИФФЕРЕНЦИАЛЬНОГО УРАВНЕНИЯ
Слайд 17ВРЕМЕННЫЕ ХАРАКТЕРИСТИКИ
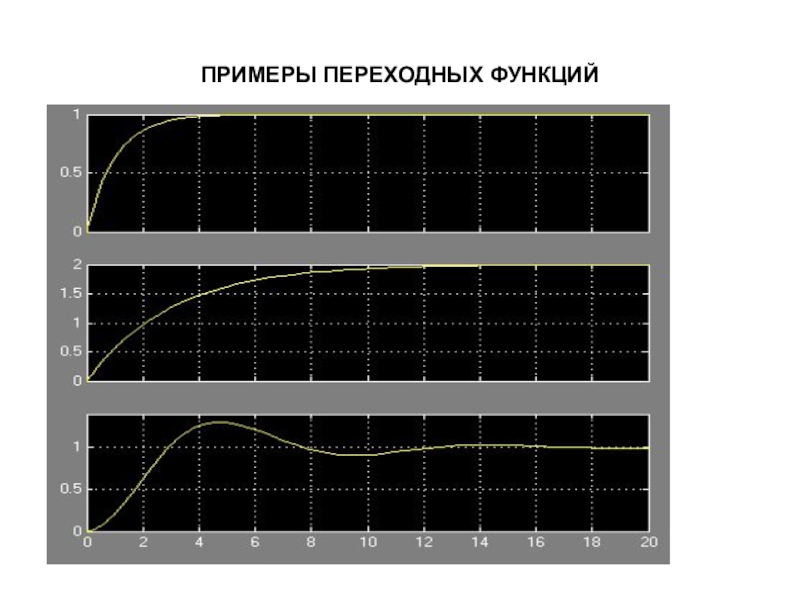
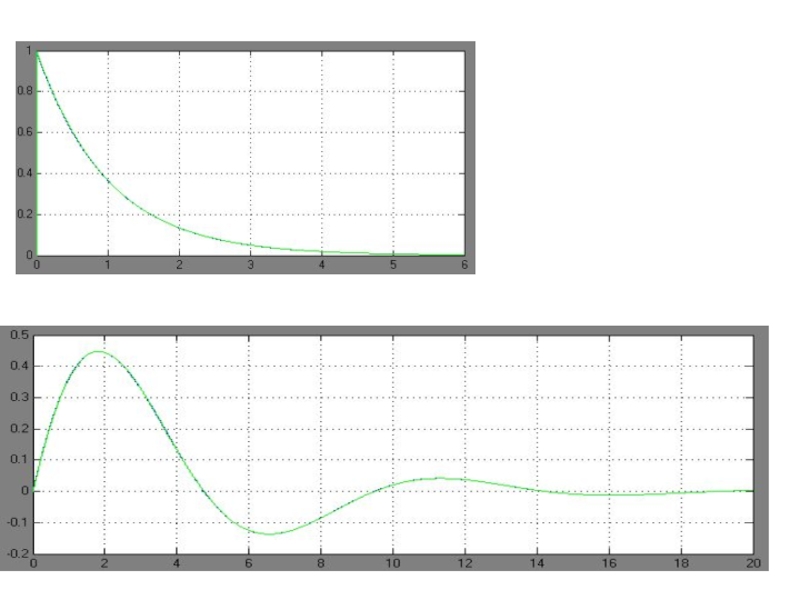
Переходная и импульсная переходная функции позволяют наглядно представить
такие важные с инженерной точки зрения свойства звена, как длительность
и характер (монотонность или колебательность) переходного процесса при резком изменении входного воздействия.
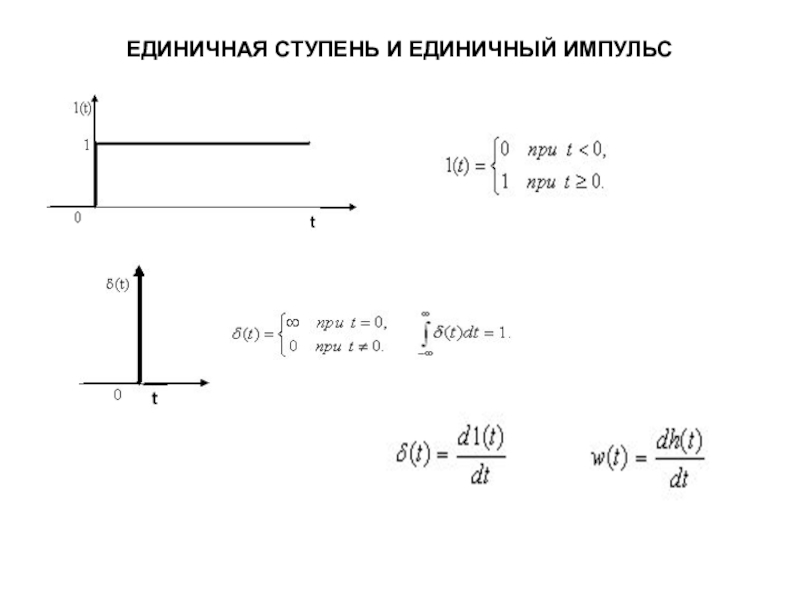
Переходная функция h(t) – это реакция выходной величины звена на единичное ступенчатое воздействие 1(t) из нулевых начальных условий до подачи воздействия.
Единичное ступенчатое воздействие 1(t) – это воздействие, которое мгновенно возрастает от нуля до единицы и далее остается неизменным.
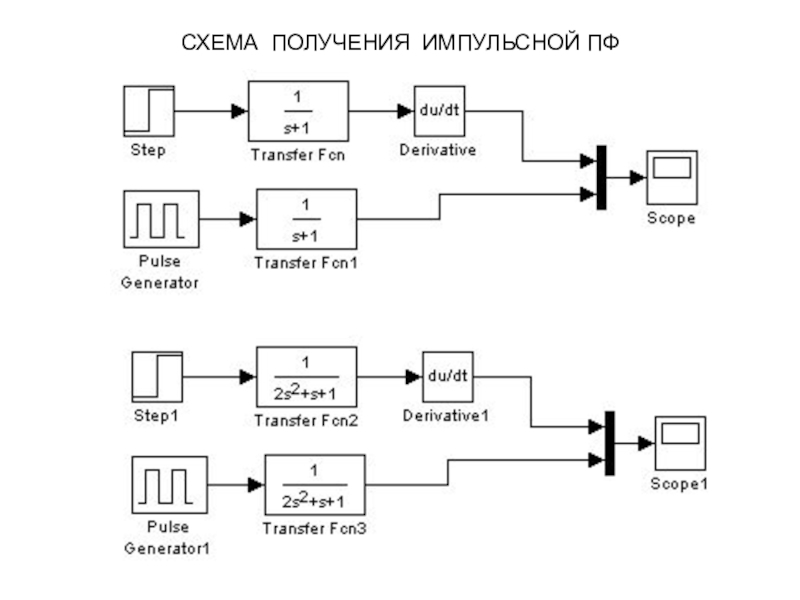
Импульсная переходная функция w(t) – это реакция выходной величины звена на единичный импульс (t) из нулевых начальных условий до подачи воздействия.
Слайд 18ЕДИНИЧНАЯ СТУПЕНЬ И ЕДИНИЧНЫЙ ИМПУЛЬС
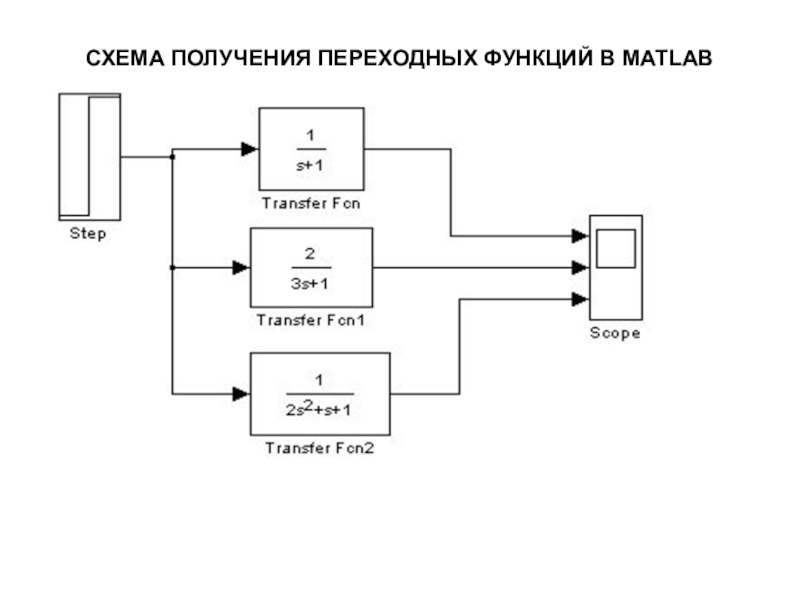
Слайд 19СХЕМА ПОЛУЧЕНИЯ ПЕРЕХОДНЫХ ФУНКЦИЙ В MATLAB
Слайд 23Передаточная функция
Передаточная функция, в отличие от дифференциального
уравнения, связывает не оригиналы X(t) и Y(t) входного и выходного
сигналов, а их изображения по Лапласу x(s) и y(s).
ПЕРЕДАТОЧНАЯ ФУНКЦИЯ – отношение изображения по Лапласу выходного сигнала Y(S) к изображению входного сигнала X(S) при нулевых начальных условиях