Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Кодирование Вещественных (Действительных) Чисел
Содержание
- 1. Кодирование Вещественных (Действительных) Чисел
- 2. Принципиальное отличие между вещественными и целыми числамиЦелые
- 3. Существует два способа представления вещественных чисел: с фиксированной и с плавающей запятой.
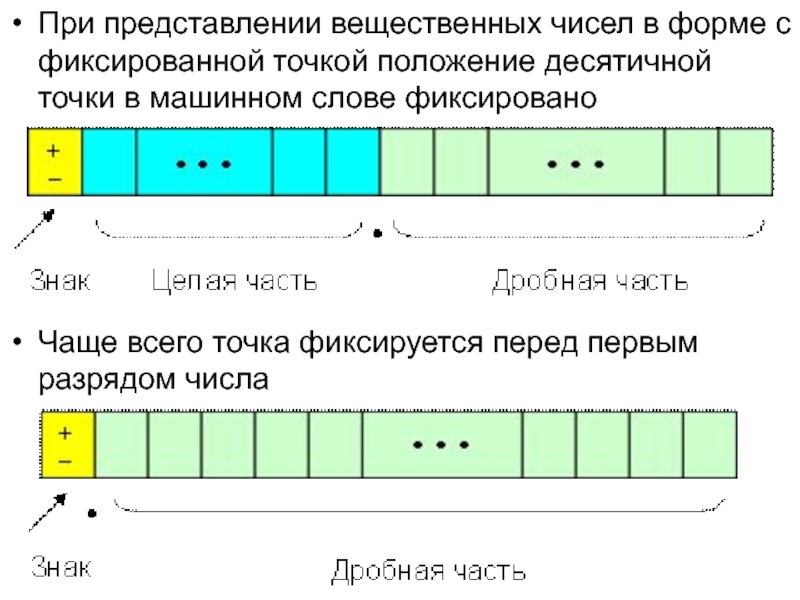
- 4. При представлении вещественных чисел в форме с
- 5. В форме с плавающей точкой вещественное число
- 6. Количество позиций, отводимых для мантиссы, определяет точность
- 7. Слайд 7
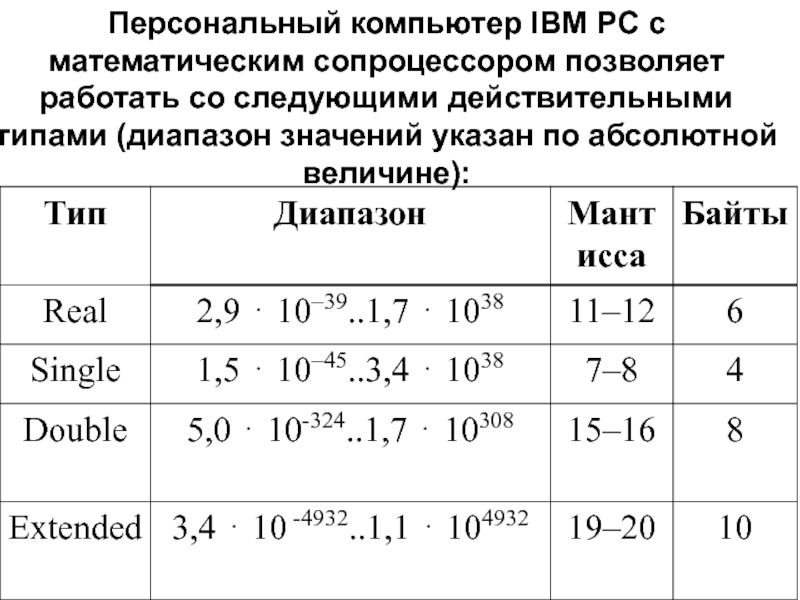
- 8. Персональный компьютер IBM PC с математическим сопроцессором
- 9. Алгоритм для получения представления действительного числа в
- 10. Теперь мы можем записать внутреннее представление числа
- 11. Пример. Запишем код числа –312,3125.1) Двоичная запись
- 12. Скачать презентанцию
Принципиальное отличие между вещественными и целыми числамиЦелые числа дискретны, и отсюда (если не брать во внимание эффект переполнения) каждому целому числу соответствует уникальный двоичный код; вещественные числа, напротив, непрерывны, а значит,
Слайды и текст этой презентации
Слайд 3Существует два способа представления вещественных чисел: с фиксированной и с
плавающей запятой.
Слайд 4При представлении вещественных чисел в форме с фиксированной точкой положение
десятичной точки в машинном слове фиксировано
Чаще всего точка фиксируется перед
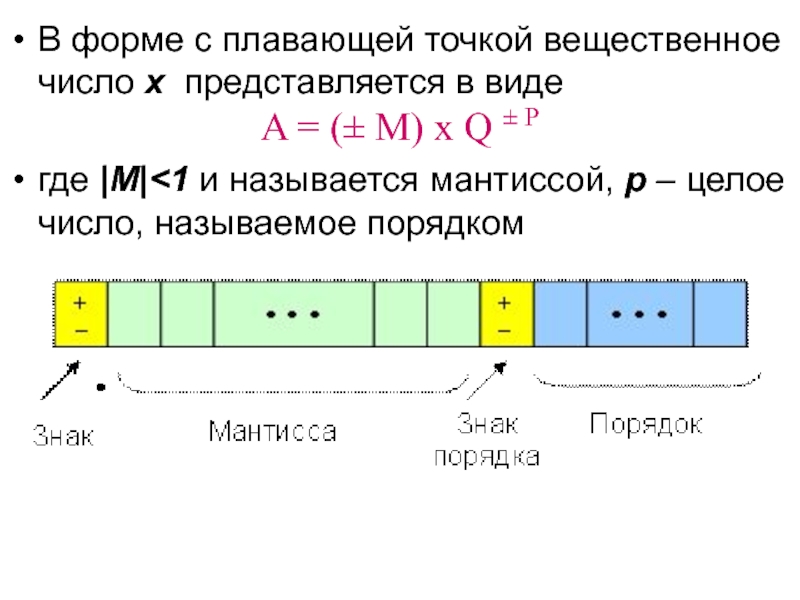
первым разрядом числа Слайд 5В форме с плавающей точкой вещественное число х представляется в
виде
A = (± M) x Q ± P
где |M|
называется мантиссой, p – целое число, называемое порядком Слайд 6Количество позиций, отводимых для мантиссы, определяет точность представления чисел, а
количество позиций, отводимых для порядка – диапазон представления чисел.
Обычно мантисса
записывается в нормализованном виде, то есть так, чтобы отсутствовали незначащие нули в старших разрядах:0.0011101 ненормализованное представление,
0.1110100 нормализованное представление.
Слайд 8Персональный компьютер IBM PC с математическим сопроцессором позволяет работать со
следующими действительными типами (диапазон значений указан по абсолютной величине):
Слайд 9Алгоритм для получения представления действительного числа в памяти ЭВМ:
1) перевести
модуль данного числа в двоичную систему счисления;
2) нормализовать двоичное число,
т.е. записать в виде M ⋅ 2p, где M — мантисса (ее целая часть равна 1(2)) и p — порядок, записанный в десятичной системе счисления;3) прибавить к порядку смещение и перевести смещенный порядок в двоичную систему счисления;
4) учитывая знак заданного числа (0 — положительное; 1 — отрицательное), выписать его представление в памяти ЭВМ.
Слайд 10Теперь мы можем записать внутреннее представление числа 25,324 в форме
с плавающей точкой.
1)Переведем его в двоичную систему счисления с
24 значащими цифрами. 25,32410= 11001,01010010111100011012
2)Запишем в форме нормализованного двоичного числа с плавающей точкой:
0,110010101001011110001101*10101
Здесь мантисса, основание системы счисления (210=102) и порядок (510=1012)записаны в двоичной системе.
3) Вычислим машинный порядок.
Мр2 = 101 + 100 0000 = 100 0101.
4) Запишем представление числа в ячейке памяти.
Знак числа
порядок
мантисса
31
0
Слайд 11Пример. Запишем код числа –312,3125.
1) Двоичная запись модуля этого числа
имеет вид 100111000,0101.
2) Имеем 100111000,0101 = 1,001110000101 ⋅ 28.
3) Получаем смещенный порядок 8 + 1023 = 1031. Далее
имеем 1031(10) = 10000000111(2).4) Окончательно
110000000111001110000101000000000000000000000000000000000000000063520