Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Комбинационные асинхронные устройства
Содержание
- 1. Комбинационные асинхронные устройства
- 2. Лекция 3. Комбинационные асинхронные устройстваКомбинационные схемы:Выходы комбинационных
- 3. Лекция 3. Комбинационные асинхронные устройстваСхема является комбинационной,
- 4. Лекция 3. Комбинационные асинхронные устройстваСхема является комбинационной,
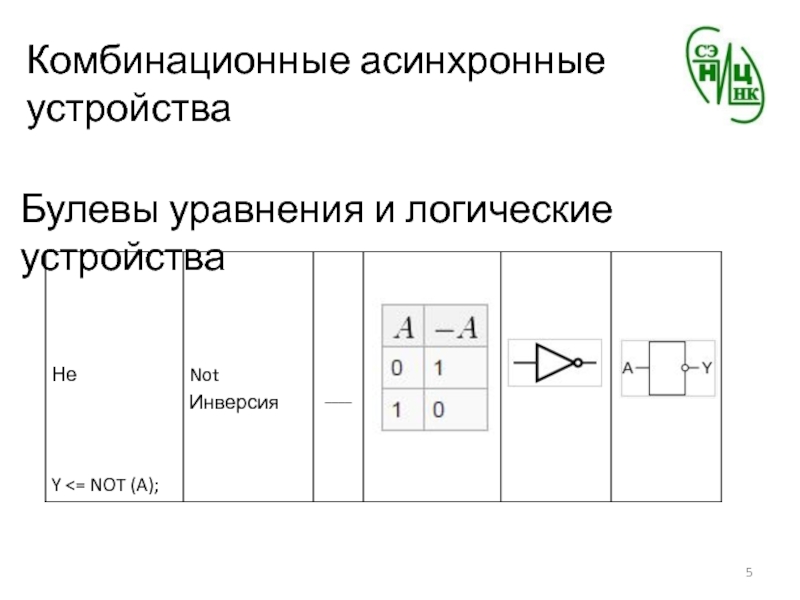
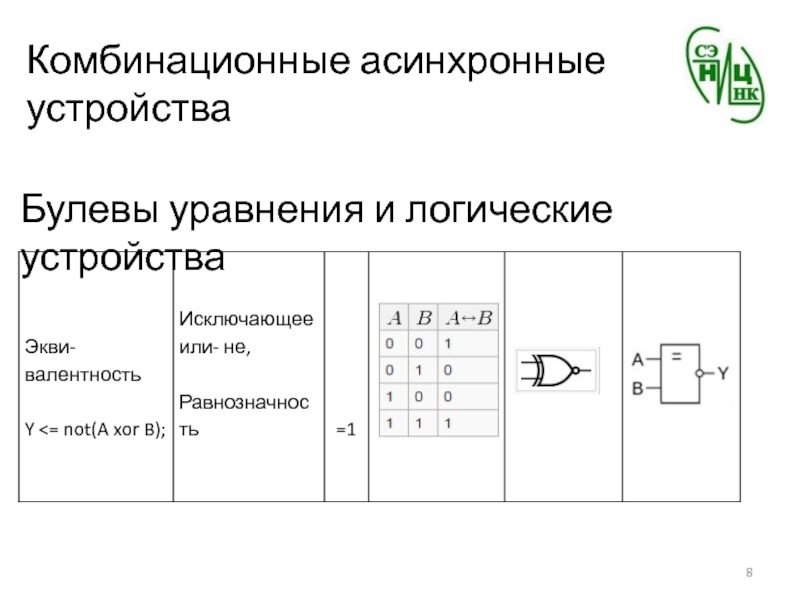
- 5. Комбинационные асинхронные устройстваБулевы уравнения и логические устройства
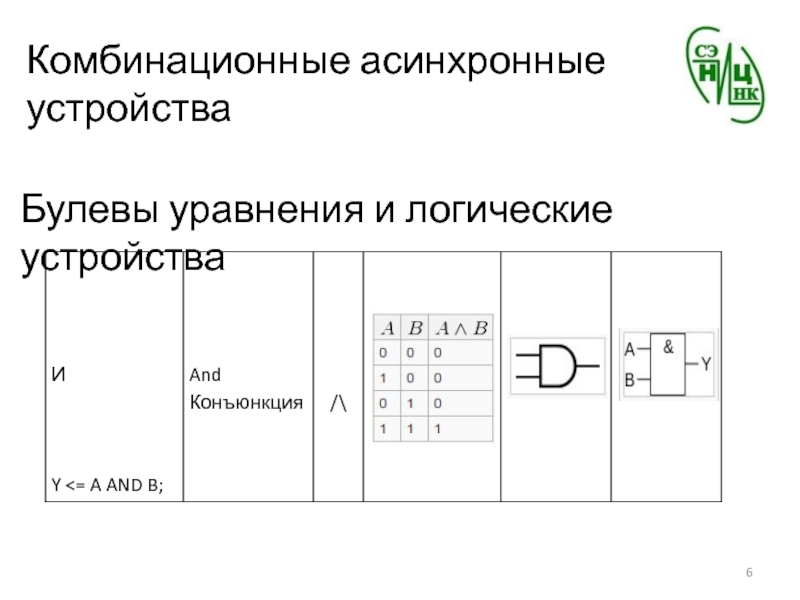
- 6. Комбинационные асинхронные устройстваБулевы уравнения и логические устройства
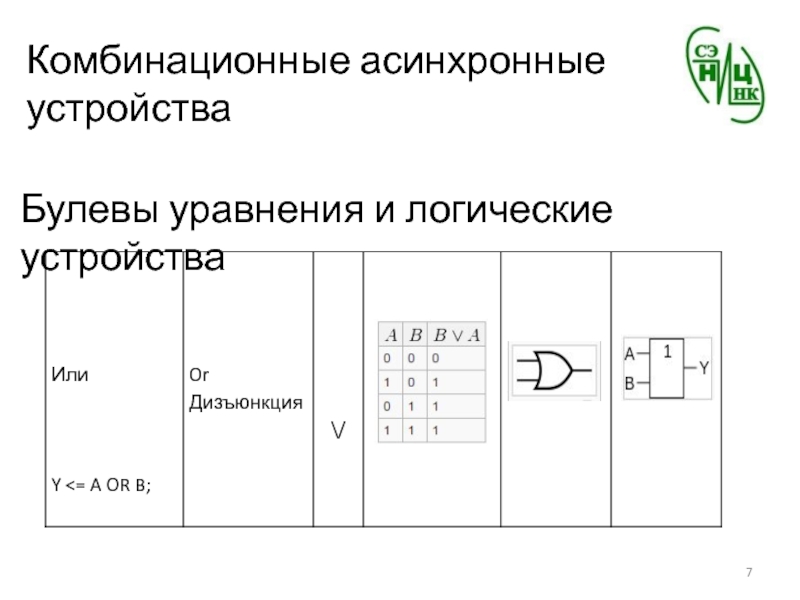
- 7. Комбинационные асинхронные устройстваБулевы уравнения и логические устройства
- 8. Комбинационные асинхронные устройстваБулевы уравнения и логические устройства
- 9. Комбинационные асинхронные устройстваБулевы уравнения и логические устройства
- 10. Комбинационные асинхронные устройстваБулевы уравнения и логические устройстваПорядок операций при анализе булевых уравненийИнверсияИИли
- 11. Комбинационные асинхронные устройстваБулевы уравнения и логические устройстваМинтерм
- 12. Комбинационные асинхронные устройстваБулевы уравнения и логические устройстваДизъюнктивная
- 13. Комбинационные асинхронные устройстваБулевы уравнения и логические устройстваДизъюнктивная
- 14. Комбинационные асинхронные устройстваБулевы уравнения и логические устройстваКонъюктивная
- 15. Комбинационные асинхронные устройстваБулевы уравнения и логические устройстваКонъюктивная
- 16. Комбинационные асинхронные устройстваБулевы уравнения и логические устройстваКонъюктивная
- 17. Комбинационные асинхронные устройстваБулевы уравнения и логические устройстваАксиомы булевой алгебры
- 18. Комбинационные асинхронные устройстваБулевы уравнения и логические устройстваТеоремы булевой алгебры для одной переменной
- 19. Комбинационные асинхронные устройстваБулевы уравнения и логические устройстваТеоремы булевой алгебры для одной переменной: схемотехнический эквивалент
- 20. Комбинационные асинхронные устройстваБулевы уравнения и логические устройстваТеоремы
- 21. Комбинационные асинхронные устройстваБулевы уравнения и логические устройстваТеоремы булевой алгебры для одной переменной: схемотехнический эквивалент
- 22. Комбинационные асинхронные устройстваБулевы уравнения и логические устройстваТеоремы булевой алгебры для нескольких переменных
- 23. Комбинационные асинхронные устройстваБулевы уравнения и логические устройстваТеорема де Моргана: схемотехнические эквиваленты
- 24. Комбинационные асинхронные устройстваБулевы уравнения и логические устройстваТеорема
- 25. Комбинационные асинхронные устройстваБулевы уравнения и логические устройстваПример минимизации логического выражения
- 26. Комбинационные асинхронные устройстваБулевы уравнения и логические устройстваОт логики к логической схемеNOTA
- 27. Комбинационные асинхронные устройстваПравила рисования логических схемВходы изображаются
- 28. Комбинационные асинхронные устройстваКарты КарноКарты Карно представляют собой
- 29. Комбинационные асинхронные устройстваКарты КарноТаблица истинности и карта
- 30. Комбинационные асинхронные устройстваКарты КарноКаждая клетка карты Карно
- 31. Комбинационные асинхронные устройстваКарты КарноКак и раньше, мы
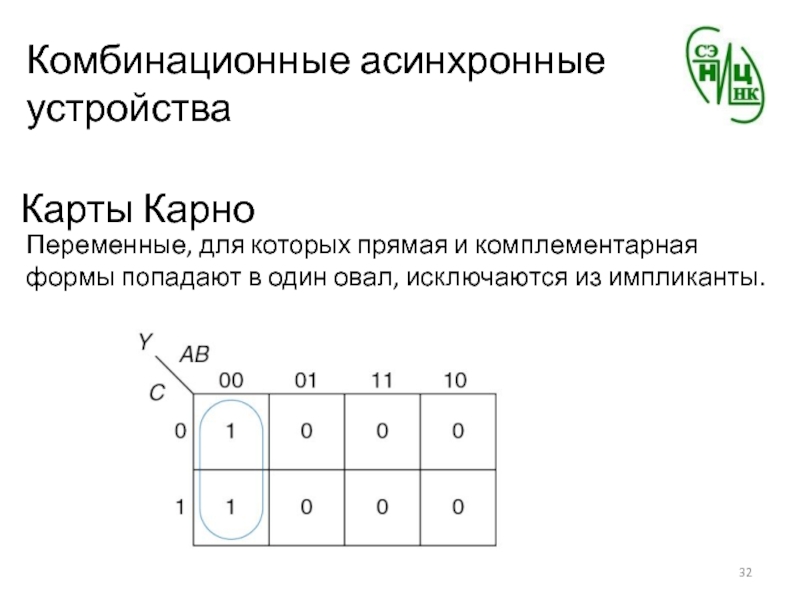
- 32. Комбинационные асинхронные устройстваКарты КарноПеременные, для которых прямая
- 33. Комбинационные асинхронные устройстваКарты КарноКарты Карно обеспечивают простой
- 34. Комбинационные асинхронные устройстваКарты КарноПравила для нахождения минимального
- 35. Комбинационные асинхронные устройстваПример разработкиЗадача: разработать декодер семисегментного
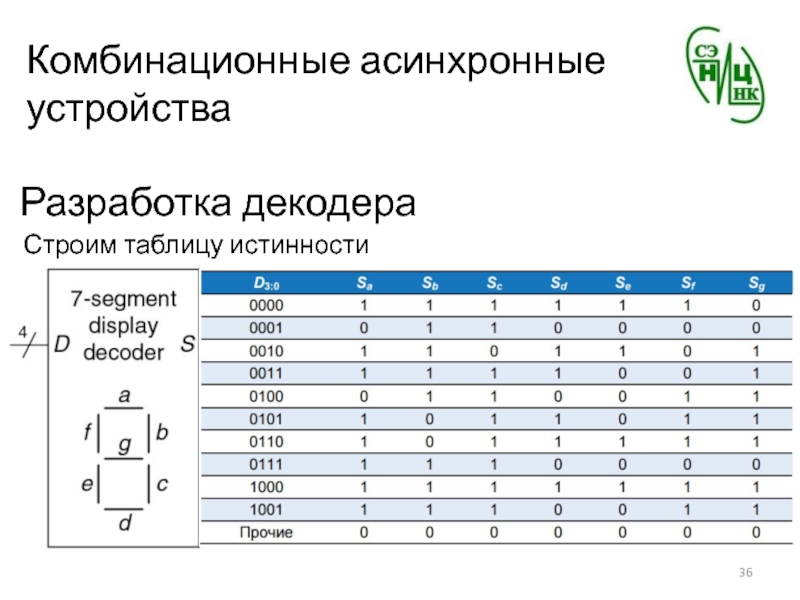
- 36. Комбинационные асинхронные устройстваРазработка декодераСтроим таблицу истинности
- 37. Комбинационные асинхронные устройстваРазработка дешифратораКаждый из семи выходов
- 38. Комбинационные асинхронные устройстваРазработка декодераОбводим первичные импликанты и записываем оптимизированные уравнения
- 39. Комбинационные асинхронные устройстваРазработка декодераОстается зарисовать схемы, соответствующие разработанным уравнениям или VHDL код:SA
- 40. Комбинационные асинхронные устройстваМультиплексорМультиплексор передает на выход один
- 41. Комбинационные асинхронные устройстваМультиплексор-- Поведенческое описание на VHDLprocess(S,
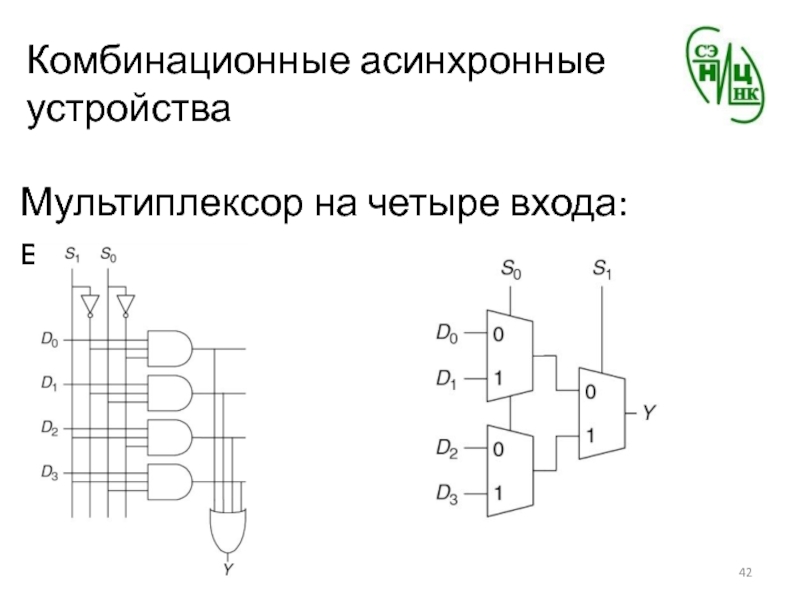
- 42. Комбинационные асинхронные устройстваМультиплексор на четыре входа: варианты
- 43. Комбинационные асинхронные устройстваМультиплексор на четыре входа: VHDL-
- 44. Комбинационные асинхронные устройстваДешифраторВ общем случае у дешифратора
- 45. Комбинационные асинхронные устройстваДешифратор 2 х 4-- описание на VHDLY0
- 46. Комбинационные асинхронные устройстваКомпаратор равенствавыдает один выходной сигнал,
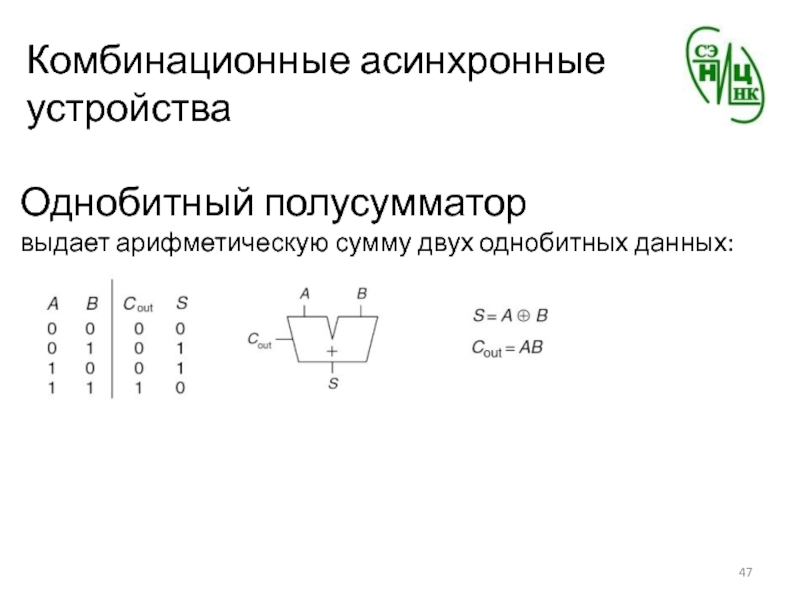
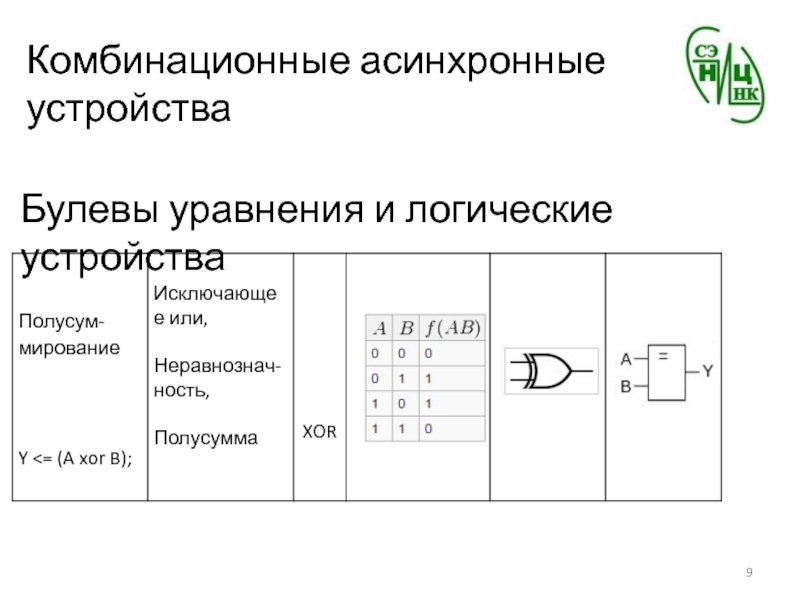
- 47. Комбинационные асинхронные устройстваОднобитный полусумматорвыдает арифметическую сумму двух однобитных данных:
- 48. Комбинационные асинхронные устройстваОднобитный полный сумматорвыдает арифметическую сумму двух однобитных данных с переносом от младшего разряда:
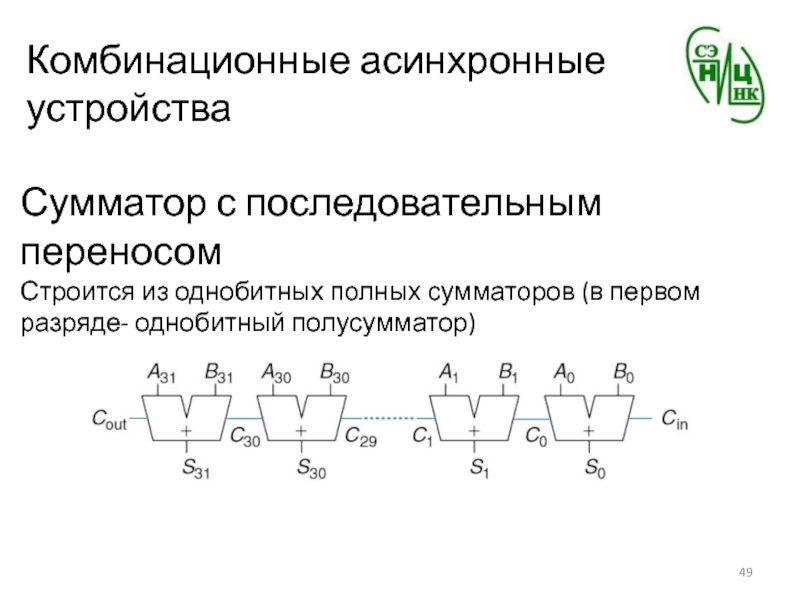
- 49. Комбинационные асинхронные устройстваСумматор с последовательным переносомСтроится из однобитных полных сумматоров (в первом разряде- однобитный полусумматор)
- 50. Cпасибо за внимание!
- 51. Скачать презентанцию
Лекция 3. Комбинационные асинхронные устройстваКомбинационные схемы:Выходы комбинационных схем зависят только от текущих значений на входах; Другими словами, такие схемы комбинируют текущие значения входных сигналов для получения значения на выходе.
Слайды и текст этой презентации
Слайд 2Лекция 3. Комбинационные асинхронные устройства
Комбинационные схемы:
Выходы комбинационных схем зависят только
от текущих значений на входах;
текущие значения входных сигналов для получения значения на выходе.
Слайд 3Лекция 3. Комбинационные асинхронные устройства
Схема является комбинационной, если
она состоит из
соединенных между собой элементов и выполнены
следующие условия:
- Каждый элемент схемы
сам является комбинационным;- Каждое соединение схемы является или входом, или подсоединено к одному выходу другого элемента схемы;
- Схема не содержит циклических путей: каждый путь в схеме проходит через любое соединение не более одного раза.
Слайд 4Лекция 3. Комбинационные асинхронные устройства
Схема является комбинационной, если
она состоит из
соединенных между собой элементов и выполнены
следующие условия:
- Каждый элемент схемы
сам является комбинационным;- Каждое соединение схемы является или входом, или подсоединено к одному выходу другого элемента схемы;
- Схема не содержит циклических путей: каждый путь в схеме проходит через любое соединение не более одного раза.
Слайд 10Комбинационные асинхронные устройства
Булевы уравнения и логические устройства
Порядок операций при анализе
булевых уравнений
Инверсия
И
Или
Слайд 11Комбинационные асинхронные устройства
Булевы уравнения и логические устройства
Минтерм и Макстерм
Минтерм (minterm,
элементарная конъюнктивная форма) –
это произведение, включающее все входы функции.
Макстерм
(maxterm, элементарная дизъюнктивная форма) – это сумма всех входов функции.
Слайд 12Комбинационные асинхронные устройства
Булевы уравнения и логические устройства
Дизъюнктивная форма
Таблица истинности для
функции N переменных содержит 2N
строк, по одной для каждой
возможной комбинации значений входов. Каждой строке в таблице истинности соответствует минтерм, который имеет значение ИСТИНА
Слайд 13Комбинационные асинхронные устройства
Булевы уравнения и логические устройства
Дизъюнктивная форма
Просуммировав нужные нам
минтермы, получим логическое
выражение в совершенной
дизъюнктивной
форме.
Слайд 14Комбинационные асинхронные устройства
Булевы уравнения и логические устройства
Конъюктивная форма
Таблица истинности для
функции N переменных содержит 2N
строк, по одной для каждой
возможной комбинации значений входов. Каждой строке в таблице
истинности соответствует
макстерм, который имеет
значение ЛОЖЬ
Слайд 15Комбинационные асинхронные устройства
Булевы уравнения и логические устройства
Конъюктивная форма
Перемножив нужные нам
макстермы,
получим логическое выражение в
совершенной конъюктивной форме.
Слайд 16Комбинационные асинхронные устройства
Булевы уравнения и логические устройства
Конъюктивная и дизъюнктивная формы
Задача:
написать совершенную дизъюнктивную и
совершенную конъюктивную формы для функции
эквивалентности.
Слайд 17Комбинационные асинхронные устройства
Булевы уравнения и логические устройства
Аксиомы булевой алгебры
Слайд 18Комбинационные асинхронные устройства
Булевы уравнения и логические устройства
Теоремы булевой алгебры для
одной переменной
Слайд 19Комбинационные асинхронные устройства
Булевы уравнения и логические устройства
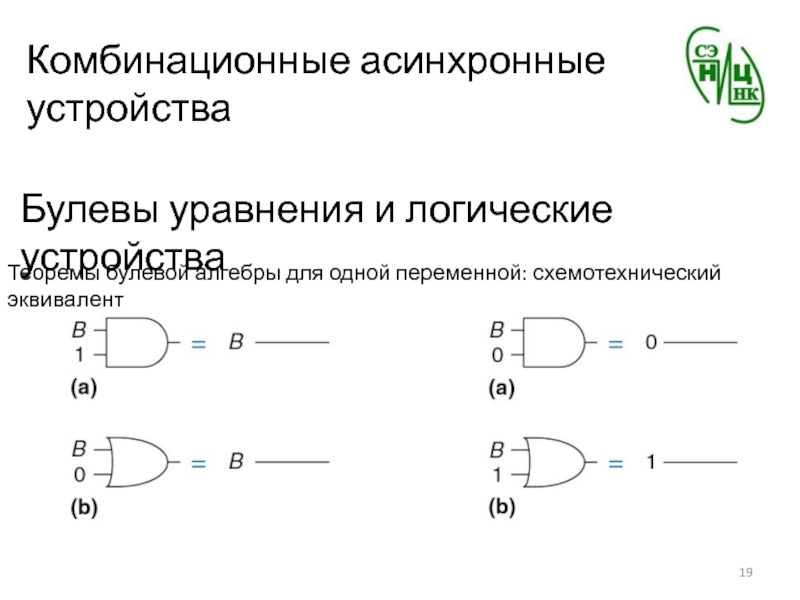
Теоремы булевой алгебры для
одной переменной: схемотехнический эквивалент
Слайд 20Комбинационные асинхронные устройства
Булевы уравнения и логические устройства
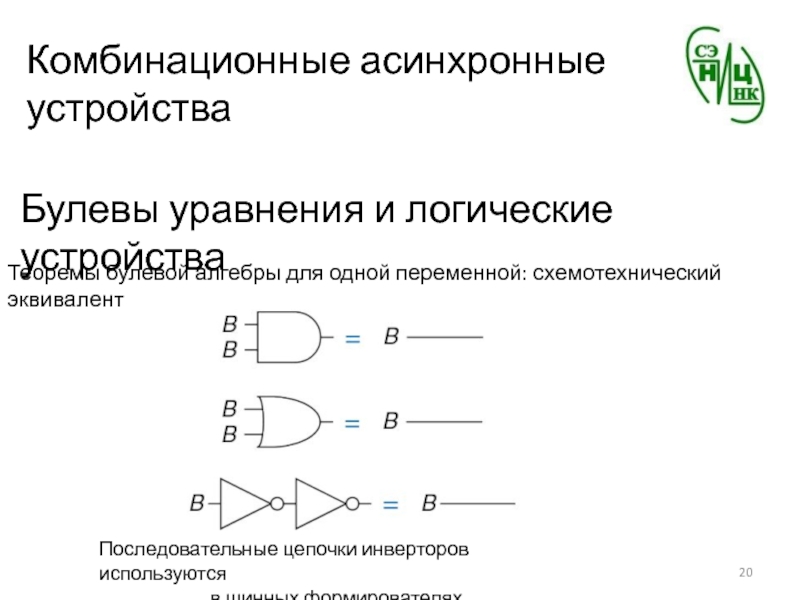
Теоремы булевой алгебры для
одной переменной: схемотехнический эквивалент
Последовательные цепочки инверторов используются
в шинных формирователях
Слайд 21Комбинационные асинхронные устройства
Булевы уравнения и логические устройства
Теоремы булевой алгебры для
одной переменной: схемотехнический эквивалент
Слайд 22Комбинационные асинхронные устройства
Булевы уравнения и логические устройства
Теоремы булевой алгебры для
нескольких переменных
Слайд 23Комбинационные асинхронные устройства
Булевы уравнения и логические устройства
Теорема де Моргана: схемотехнические
эквиваленты
Слайд 24Комбинационные асинхронные устройства
Булевы уравнения и логические устройства
Теорема де Моргана: словами
Перемещение
инверсии назад (от выхода) или вперед (от входов) меняет тип
элемента с И на ИЛИ и наоборот;Перемещение инверсии с выхода назад ко входам приводит к тому, что на всех входах появляется инверсия;
Перемещение инверсии со всех входов элемента к выходу приводит к появлению инверсии на выходе.
Слайд 25Комбинационные асинхронные устройства
Булевы уравнения и логические устройства
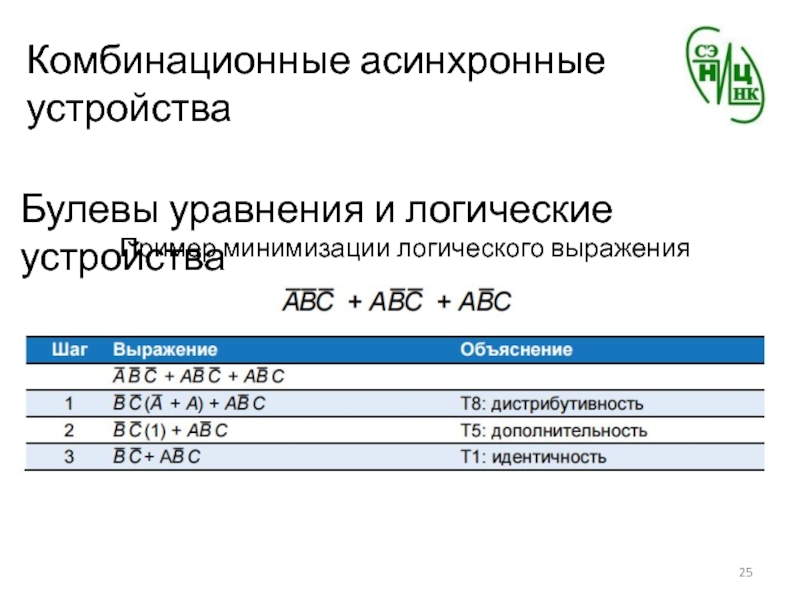
Пример минимизации логического выражения
Слайд 26Комбинационные асинхронные устройства
Булевы уравнения и логические устройства
От логики к логической
схеме
NOTA
NOT(b); MINTERM2 <= A AND NOTB AND NOTC;NOTC <= NOT(C); MINTERM3 <= A AND NOTB AND C;
Y <= MINTERM1 OR MINTERM2 OR MINTERM3;
Слайд 27Комбинационные асинхронные устройства
Правила рисования логических схем
Входы изображаются на левой (или
верхней) части схемы;
Выходы изображаются на правой (или нижней) части схемы;
Всегда,
когда это возможно, элементы необходимо изображать слева направо;Проводники лучше изображать прямыми линиями, чем линиями с множеством углов (неровные рваные линии отвлекают внимание: приходится следить за тем, куда ведут провода, а не думать о том, что делает схема);
Проводники всегда должны соединяться в виде буквы «Т»;
Проводники, пересекающиеся без точки, не имеют соединения друг с другом.
Слайд 28Комбинационные асинхронные устройства
Карты Карно
Карты Карно представляют собой наглядный метод для
упрощения булевых уравнений. Карты Карно очень удобны в случаях, когда
уравнение содержит до четырёх переменных. Но, что более важно, они дают понимание сути при работе с логическими выражениями.Логическая минимизация осуществляется путем склейки термов. Два терма, включающие в себя импликанту P и два логических значения некоторой переменной A, объединяются, при этом переменная A исключается. Карты Карно позволяют легко находить термы, которые можно склеить, располагая их в виде таблицы.
Слайд 29Комбинационные асинхронные устройства
Карты Карно
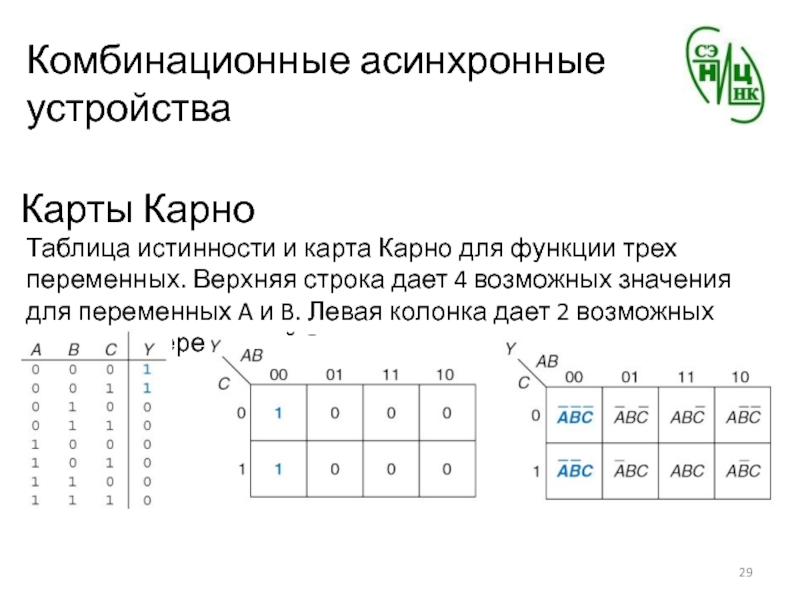
Таблица истинности и карта Карно для функции
трех переменных. Верхняя строка дает 4 возможных значения для переменных
A и B. Левая колонка дает 2 возможных значения переменной C.
Слайд 30Комбинационные асинхронные устройства
Карты Карно
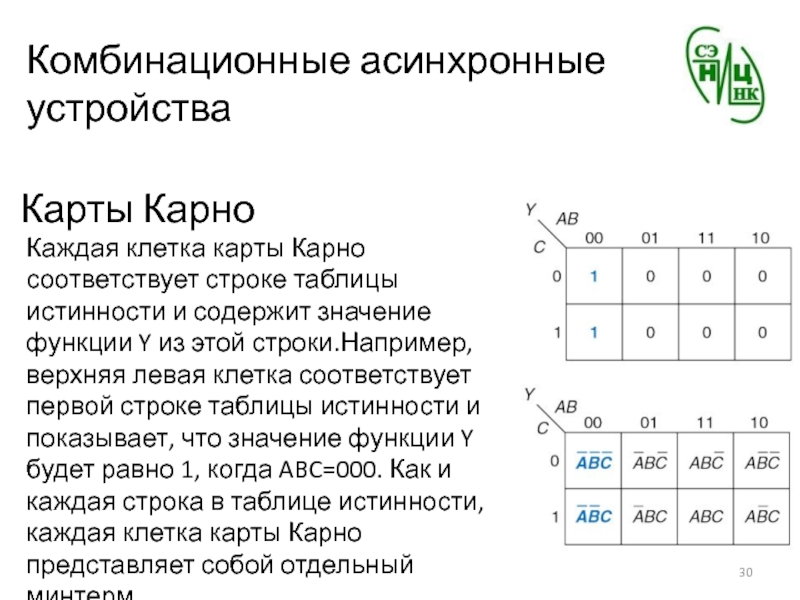
Каждая клетка карты Карно соответствует строке таблицы
истинности и содержит значение функции Y из этой строки.Например, верхняя
левая клетка соответствует первой строке таблицы истинности и показывает, что значение функции Y будет равно 1, когда ABC=000. Как и каждая строка в таблице истинности, каждая клетка карты Карно представляет собой отдельный минтерм.
Слайд 31Комбинационные асинхронные устройства
Карты Карно
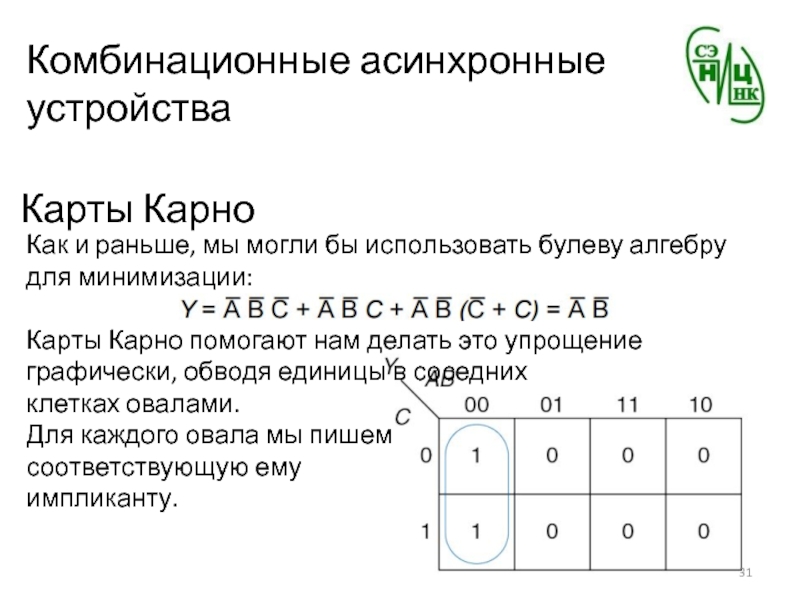
Как и раньше, мы могли бы использовать
булеву алгебру для минимизации:
Карты Карно помогают нам делать это упрощение
графически, обводя единицы в соседних клетках овалами.
Для каждого овала мы пишем
соответствующую ему
импликанту.
Слайд 32Комбинационные асинхронные устройства
Карты Карно
Переменные, для которых прямая и комплементарная формы
попадают в один овал, исключаются из импликанты.
Слайд 33Комбинационные асинхронные устройства
Карты Карно
Карты Карно обеспечивают простой визуальный способ минимизации
логических выражений. Просто обведите все прямоугольные блоки с единицами на
карте, используя наименьшее возможное число овалов. Каждый овал должен быть максимально большим. Затем прочитайте все импликанты, которые обведены.Максимально возможный овал является первичной импликантой.
Слайд 34Комбинационные асинхронные устройства
Карты Карно
Правила для нахождения минимального уравнения из карт
Карно: Использовать меньше всего овалов, необходимых для покрытия всех 1;
Все
клетки в каждом овале обязаны содержать 1;Каждый овал должен охватывать блок, число клеток которого в каждом направлении равно степени двойки (то есть 1, 2 или 4);
Каждый овал должен настолько большим, насколько это возможно;
Овал может связывать края карты Карно;
Единица на карте Карно может быть обведена сколько угодно раз, если это позволяет уменьшить число овалов, которые будут использоваться.
Слайд 35Комбинационные асинхронные устройства
Пример разработки
Задача: разработать декодер
семисегментного индикатора.
Декодер получает
на вход четырехбитные
данные D[3:0] и формирует семь выходов для
управления светодиодами для показа цифр
от 0 до 9.
Семь выходов часто называют сегментами
от a до g, или Sa–Sg
![Комбинационные асинхронные устройстваПример разработкиЗадача: разработать декодер семисегментного индикатора. Декодер получает на вход четырехбитные данные D[3:0] и формирует](/img/thumbs/c19fb05cca40ee265a6e5b2b6623fa5e-800x.jpg "Комбинационные асинхронные устройства Комбинационные асинхронные устройстваПример разработкиЗадача: разработать декодер семисегментного индикатора. Декодер получает на")
Слайд 37Комбинационные асинхронные устройства
Разработка дешифратора
Каждый из семи выходов является независимой функцией
от четырех переменных. Карты Карно для выходов Sa и Sb:
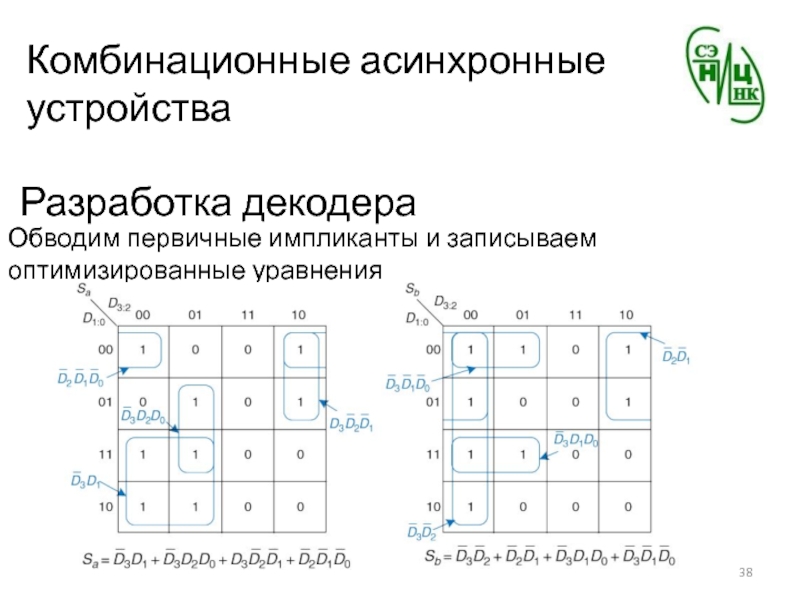
Слайд 38Комбинационные асинхронные устройства
Разработка декодера
Обводим первичные импликанты и записываем оптимизированные уравнения
Слайд 39Комбинационные асинхронные устройства
Разработка декодера
Остается зарисовать схемы, соответствующие разработанным уравнениям или
VHDL код:
SA
(NOT(D3) AND D2 AND D0) OR (D3 AND NOT(D2) AND NOT(D1)) OR
(NOT (D2) AND NOT (D1) AND NOT (D0));
SB <= (NOT(D3) AND NOT(D2)) OR
(NOT(D2) AND NOT (D1)) OR
(NOT (D3) AND NOT(D1) AND NOT (D0));
Слайд 40Комбинационные асинхронные устройства
Мультиплексор
Мультиплексор передает на выход
один из нескольких входных сигналов
данных, основываясь на сигнале выбора:
Для двухвходового мультиплексора:
Если S =
0, выход Y = D0,
Если S = 1, то выход Y = D1.
S также называют управляющим
сигналом, так как он управляет
поведением мультиплексора. 
Слайд 41Комбинационные асинхронные устройства
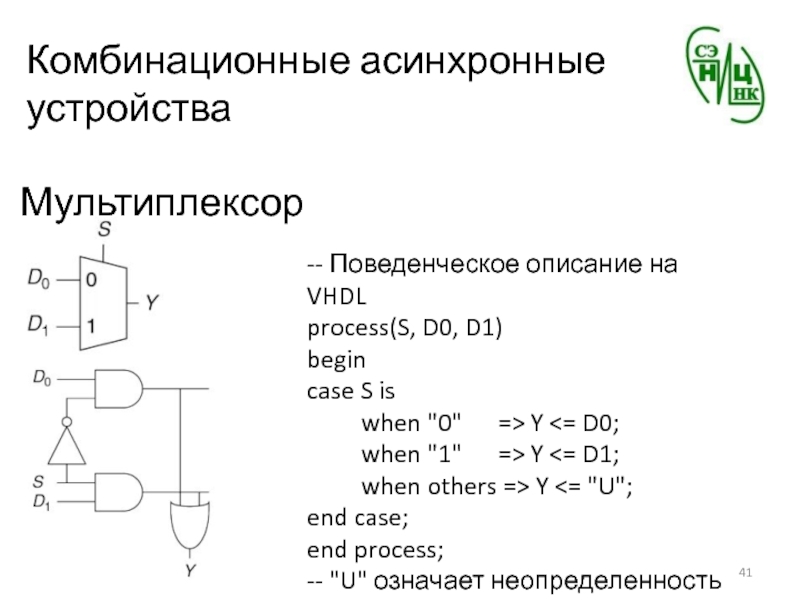
Мультиплексор
-- Поведенческое описание на VHDL
process(S, D0, D1)
begin
case S
is
when "0" =>
Y <= D0;when "1" => Y <= D1;
when others => Y <= "U";
end case;
end process;
-- "U" означает неопределенность
Слайд 43Комбинационные асинхронные устройства
Мультиплексор на четыре входа: VHDL- код
library ieee;
use ieee.std_logic_1164.all;
entity
mux4 is
port(a, b, c, d: in std_logic_vector(7 downto 0);
s:
in std_logic_vector(1 downto 0);x: out std_logic_vector(7 downto 0));
end mux4;
architecture cond_arch of mux4 is
begin
x <= a when (s = "00") else
b when (s = "01") else
c when (s = "10") else
d;
end cond_arch;
-- Конструкция when else должна быть исчерпывающей !
Слайд 44Комбинационные асинхронные устройства
Дешифратор
В общем случае у дешифратора имеется N входов
и 2N выходов. Он выдает единицу строго на один из
выходов в зависимости от набора входных значений.
Слайд 45Комбинационные асинхронные устройства
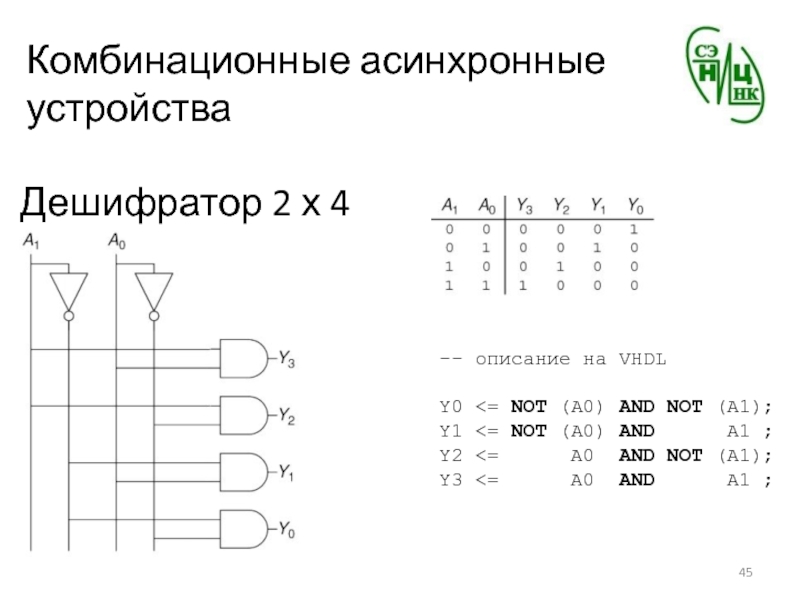
Дешифратор 2 х 4
-- описание на VHDL
Y0
NOT (A0) AND NOT (A1);
Y1
A1 ;Y2 <= A0 AND NOT (A1);
Y3 <= A0 AND A1 ;
Слайд 46Комбинационные асинхронные устройства
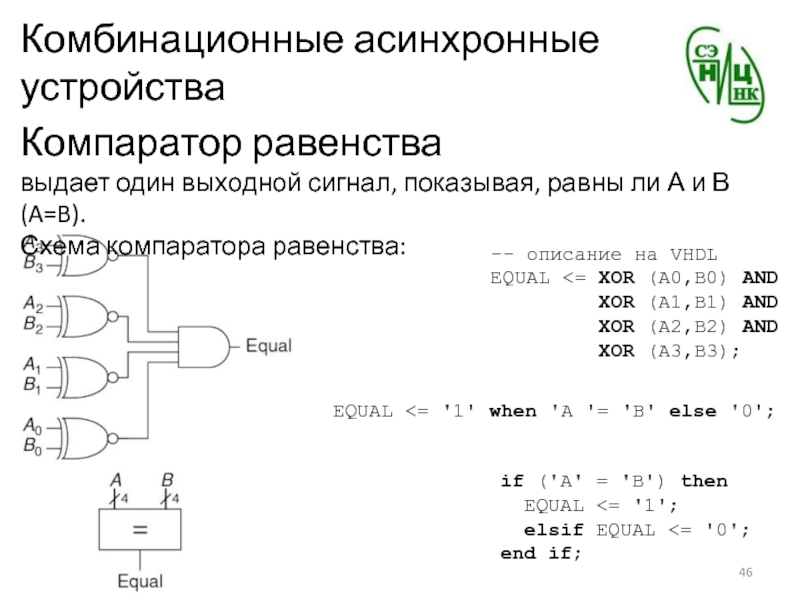
Компаратор равенства
выдает один выходной сигнал, показывая, равны ли
А и В (A=B).
Схема компаратора равенства:
-- описание на VHDL
EQUAL
XOR (A0,B0) AND
XOR (A1,B1) AND
XOR (A2,B2) AND
XOR (A3,B3);EQUAL <= '1' when 'A '= 'B' else '0';
if ('A' = 'B') then
EQUAL <= '1';
elsif EQUAL <= '0';
end if;
Слайд 47Комбинационные асинхронные устройства
Однобитный полусумматор
выдает арифметическую сумму двух однобитных данных:
Слайд 48Комбинационные асинхронные устройства
Однобитный полный сумматор
выдает арифметическую сумму двух однобитных данных
с переносом от младшего разряда:
Слайд 49Комбинационные асинхронные устройства
Сумматор с последовательным переносом
Строится из однобитных полных сумматоров
(в первом разряде- однобитный полусумматор)
