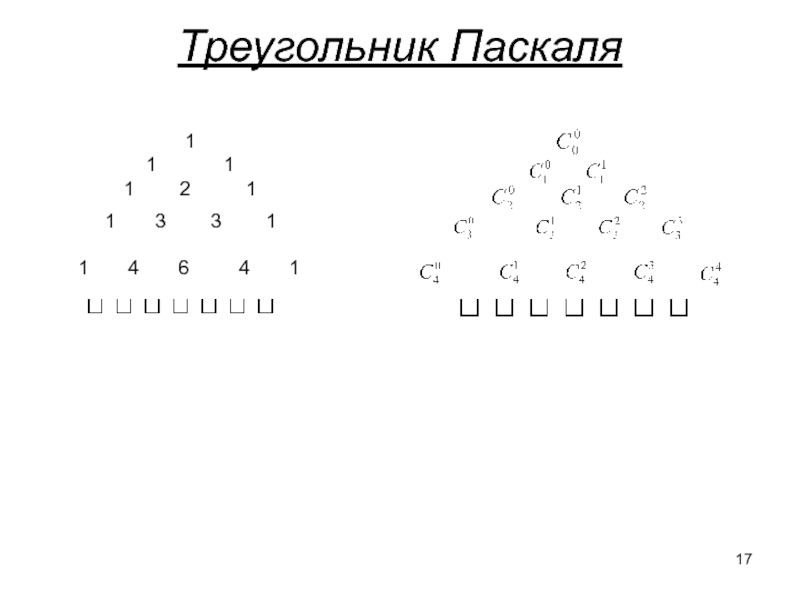
Слайд 2Комбинаторика
Комбинаторика – раздел математики, посвященный подсчету количеств разных комбинаций элементов
некоторого, обычно конечного, множества
Задачи:
1) Сколькими способами 6 разных папок
с документами можно расставить на полке?
2) При расследовании хищения установлено, что у преступника шестизначный номер телефона, в котором все цифры различны и нет нулей. Следователь, полагая, что перебор этих номеров достаточно будет одного - двух часов, доложил о раскрытии преступления. Прав ли он?
3) На иномарке, скрывшейся с места ДТП, был трехзначный номер, в котором первая цифра 2. Сколько номеров необходимо проверить по картотеке ГИБДД, чтобы найти нарушителя?
Слайд 3Принципы комбинаторики
Принцип сложения
Основные принципы комбинаторики:
Принцип сложения.
Принцип умножения.
Принцип сложения
Задача 1: В
группе 7 девушек и 8 юношей. Сколькими способами можно выбрать
1 человека для работы у доски?
Решение: 7+8=15
Задача 2: В группе 7 человек имеют «5» по математике, 9 человек – «5» по философии. В сессии 2 экзамена. Известно, что 4 человека сдали сессию отлично. Сколько человек имеют хотя бы одну пятерку в сессии?
Решение: 7+9-4=12
Слайд 4Принцип сложения
Принцип сложения: Если объект a можно получить n способами,
объект b – m способами, то объект «a или b»
можно получить n+m-k способами, где k – это количество повторяющихся способов.
Теоретико-множественная формулировка
Слайд 5Принцип умножения
Задача: На вершину горы ведут 5 дорог. Сколькими способами
можно подняться на гору и спуститься с нее?
Решение: 5∙5=25.
Принцип умножения:
если объект a можно получить n способами, объект b – m способами, то объект «a и b» можно получить m∙n способами.
Теоретико-множественная формулировка
Слайд 6Задачи
Из 3 экземпляров учебника алгебры, 5 экземпляров учебника геометрии
и 7 экземпляров учебника истории нужно выбрать по одному экземпляру
каждого учебника. Сколькими способами это можно сделать?
Решение. По принципу умножения
Слайд 7Задачи
От дома до школы существует 6 маршрутов. Сколькими способами
можно дойти до школы и вернуться, если дорога «туда» и
«обратно» идет по разных маршрутам?
Решение. По принципу умножения
Слайд 8Задачи
В корзине лежат 7 различных яблок и 5 апельсинов. Яша
выбирает из нее яблоко или апельсин, после чего Полина берет
яблоко и апельсин. В каком случае Полина имеет большую свободу выбора: если Яша взял яблоко или если он взял апельсин?
Решение. Если Яша взял яблоко, то по принципу умножения Полина может осуществить свой выбор
способами. Если Яша взял апельсин,
то - способами.
В первом случае у Полины свобода выбора большая.
Слайд 9Замечание
Например,
Считают, что 0!=1
читается «n факториал» и вычисляется по
формуле
Слайд 10Определение 1
Перестановкой n элементного множества называется упорядоченный набор неповторяющихся элементов
этого множества длины n.
Пример:
перестановки:
Число размещений n – элементного множества
обозначают Pn и вычисляется по формуле:
Задача: В команде 6 человек. Сколькими способами можно осуществить построение?
Перестановки без повторений
Слайд 11Перестановки с повторениями
Определение 2
Число перестановок n – элементов, в котором
элементов i –того типа (
) вычисляется по формуле
Задача: Сколько слов можно составить, переставив буквы в слове «экзамен», а в слове «математика»?
Решение:
Слайд 12Размещение без повторений
Определение 3
k -размещением без повторений элементов множества
А называется упорядоченный набор длины k попарно различных элементов множества
А.
Пример: - 2 размещения:
Число k- размещений n элементного множества обозначается
и вычисляется по формуле:
Задача: В соревновании участвуют 12 команд, сколькими способами они могут занять призовые места?
Слайд 13Размещения с повторениями
Определение 4
k – размещением с повторениями n–элементного множества
называется упорядоченный набор длины k элементов данного множества.
Пример
2- размещения
с повторениями:
Число k – размещений с повторениями вычисляется по формуле:
Задача: Сколько существует номеров машин?
Слайд 14Сочетания
Определение 1
k-сочетанием множества А называется неупорядоченный набор попарно различных
элементов множества А длины k. Другими словами k-сочетание – это
k-элементное подмножество множества А
Пример: . 2- сочетания:
Число k- сочетаний n-элементного множества обозначается и вычисляется по формуле
Слайд 15Свойства сочетаний
1)
Доказательство:
2)
Доказательство:
Слайд 16Свойства сочетаний
3) Бином Ньютона:
Следствия из бинома Ньютона:
получается из
бинома Ньютона при
получается из бинома Ньютона при
Равенство
Равенство
Слайд 18Сочетание с повторениями
Определение 2
k-сочетанием с повторениями n элементного множества,
называется неупорядоченный набор элементов данного множества длины k.
Пример: А=
2 сочетания с повторениями:
Число k-сочетание с повторениями n – элементного множества обозначается:
Слайд 19Сочетания с повторениями
Теорема 3
Число k-сочетание с повторениями n – элементного
множества вычисляется по формуле:
Доказательство:
Лемма. Число наборов из m нулей
и n единиц равно
Закодируем k - сочетания с повторениями наборами из 0 и 1, отделяя нулями группы элементов одного типа. Количество 1 равно k, а количество нулей
(n-1). Число таких кодов равно
Слайд 22Задачи
1)Сколькими способами можно составить список из 8 студентов, если у
них различные инициалы?
Решение
Задача сводится к подсчету числа перестановок ФИО.
Слайд 23Задачи
2)Сколькими способами можно составить список 8 студентов, так, чтобы два
указанных студента располагались рядом?
Решение
Можно считать двоих указанных студентов за один
объект и считать число перестановок уже 7 объектов, т.е.
Так как этих двоих можно переставлять местами друг с другом, необходимо умножить результат на 2!
Слайд 24Задачи
3) Сколькими способами можно разделить 11 спортсменов на 3 группы
по 4, 5 и 2 человека соответственно?
Решение. Сделаем карточки: четыре
карточки с номером 1, пять карточек с номером 2 и две карточки с номером 3. Будем раздавать эти карточки с номерами групп спортсменам, и каждый способ раздачи будет соответствовать разбиению спортсменов на группы. Таким образом нам необходимо посчитать число перестановок 11 карточек, среди которых четыре карточки с одинаковым номером 1, пять карточек с номером 2 и две карточки с номером 3.
Слайд 25Задачи
4) Сколькими способами можно вызвать по очереди к доске 4
учеников из 7?
Решение. Задача сводится к подсчету числа размещений из
7 элементов по 4
Слайд 26Задачи
5)Сколько существует четырехзначных чисел, у которых все цифры различны?
Решение. В
разряде единиц тысяч не может быть нуля, т.е возможны 9
вариантов цифры.
В остальных трех разрядах не может быть цифры, стоящей в разряде единиц тысяч (так как все цифры должны быть различны), поэтому число вариантов вычислим по формуле размещений без повторений из 9 по 3
По правилу умножения получим
Слайд 27Задачи
6)Сколько существует двоичных чисел, длина которых не превосходит 10?
Решение. Задача
сводится к подсчету числа размещений с повторениями из двух элементов
по 10
Слайд 28Задачи
7)В лифт 9 этажного дома зашли 7 человек. Сколькими способами
они могут распределиться по этажам дома?
Решение. Очевидно, что на первом
этаже никому не надо выходить. Каждый из 7 человек может выбрать любой из 8 этажей, поэтому по правилу умножения получим
Можно так же применить формулу для числа размещений с повторениями из 8 (этажей) по 7(на каждого человека по одному этажу)
Слайд 29Задачи
8)Сколько чисел, меньше 10000 можно написать с помощью цифр 2,7,0?
Решение.
Так как среди цифр есть 0, то, например запись 0227
соответствует числу 227, запись 0072 соответствует числу 72, а запись 0007 соответствует числу 7. Таким образом, задачу можно решить, используя формулу числа размещений с повторениями
Слайд 30Задачи
1) В почтовом отделении продают 10 сортов открыток. Сколькими способами
можно купить в нем 8 различных открыток? Сколькими способами можно
купить 8 открыток?
2) Сколькими способами можно раздать 5 одинаковых апельсинов, 3 банана, 7 яблок между 4 людьми?
Слайд 31Задачи
3) Сколькими способами можно закодировать дверь?
4) Сколько существует трехзначных чисел?
5)
Абонент забыл последние 3 цифры телефонного номера. Помня, что эти
цифры различны, он набирает номер наугад. Сколько номеров ему нужно перебрать, если он невезучий человек?
Слайд 32Задачи
6) В компьютерном салоне продают мониторы 5 марок. Сколькими способами
организация может купить в нем 3 монитора различных марок? Сколькими
способами можно купить 3 монитора?
Решение. Ответ на первый вопрос получим с помощью формулы числа сочетаний без повторений, так как мониторы различные
На второй вопрос ответим, используя формулу числа сочетаний с повторениями, так как не сказано, что мониторы различных марок, значит марки могут повторяться
Слайд 33Задачи
7)В группе 8 юношей и 9 девушек. Сколькими способами можно
выбрать группу студентов, состоящей из 4 юношей и 3 девушек?
Решение.
Четырех юношей выберем из 8, троих девушек – из 9. По правилу умножения получим
Слайд 34Задачи
8)Используя бином Ньютона, раскрыть скобки .
Решение.
Слайд 35Задачи
9)Сколькими способами можно раздать 7 одинаковых апельсинов между тремя детьми?
Решение.
Так как апельсины одинаковые, их вообще нельзя использовать в качестве
7 различных элементов множества.
Рассмотрим множество, состоящее из троих детей. Будем выбирать детей для апельсинов. Используем формулу числа сочетаний с повторениями, так как одному ребенку может достаться несколько апельсинов, а может не достаться ни одного.
Слайд 36Задачи
10) Сколькими способами можно распределить 5 одинаковых принтеров, 3 телефонных
аппарата, 7 мониторов между 4 фирмами?
Решение. Распределим сначала принтеры, затем
телефонные аппараты, и, наконец, мониторы. Используя правило умножения, получим