Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
КОНСТРУИРОВАНИЕ АЛГОРИТМОВ АЛГОРИТМИЗАЦИЯ И ПРОГРАММИРОВАНИЕ
Содержание
- 1. КОНСТРУИРОВАНИЕ АЛГОРИТМОВ АЛГОРИТМИЗАЦИЯ И ПРОГРАММИРОВАНИЕ
- 2. Ключевые слова последовательное построение алгоритма вспомогательный алгоритм формальные параметры фактические параметры рекурсивный алгоритм
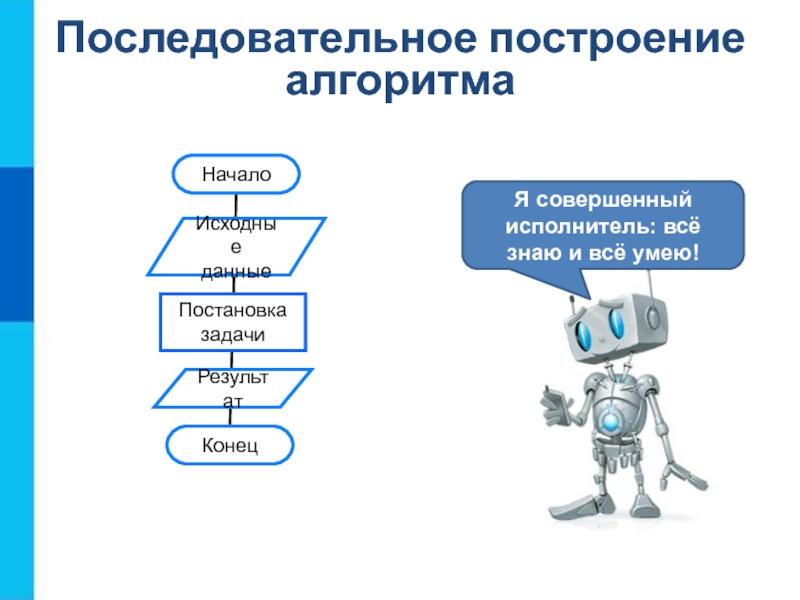
- 3. Последовательное построение алгоритмаЯ совершенный исполнитель: всё знаю и всё умею!
- 4. Последовательное построение алгоритмаУпрощение командпостановки задачиЗадача разбивается на
- 5. Разработка алгоритма методом последовательного уточнения для исполнителя
- 6. Укрупнённый план действий Робота 1. Закраска всех
- 7. 1. Закраска всех клеток коридора, находящихся левее
- 8. 2. Возвращение Робота в коридор в исходную
- 9. 3. Закраска всех клеток коридора, находящихся правее
- 10. 4.Возвращение Робота в коридор в исходную точку:
- 11. алгнач влево нц пока сверху
- 12. Вспомогательный алгоритм Вспомогательный алгоритм – алгоритм, целиком
- 13. Алгоритм вычисления степени y = ax, где
- 14. Блок-схема решения задачи:
- 15. Формальные параметры используются при описании алгоритма. Фактические
- 16. Схема вызова вспомогательного алгоритма
- 17. Пример. Алгоритм вычисления степени с натуральным показателем
- 18. Снежинка КохаПример. Рассмотрим алгоритм построения геометрической фигуры,
- 19. Самое главноеМетод последовательного построения алгоритма: исходная задача
- 20. Вопросы и задания4. Известен рост каждого из
- 21. Вопросы и задания5. В ряду из десяти
- 22. Вопросы и задания9. Какие алгоритмы называют рекурсивными?Приведите
- 23. Вопросы и заданияабв10. Составьте алгоритмы, под управлением которых Робот закрасит указанные клетки.
- 24. Опорный конспектМетод последовательного построения алгоритма – один
- 25. Скачать презентанцию
Слайды и текст этой презентации
Слайд 2Ключевые слова
последовательное построение алгоритма
вспомогательный алгоритм
формальные параметры
фактические
параметры
Слайд 4Последовательное построение алгоритма
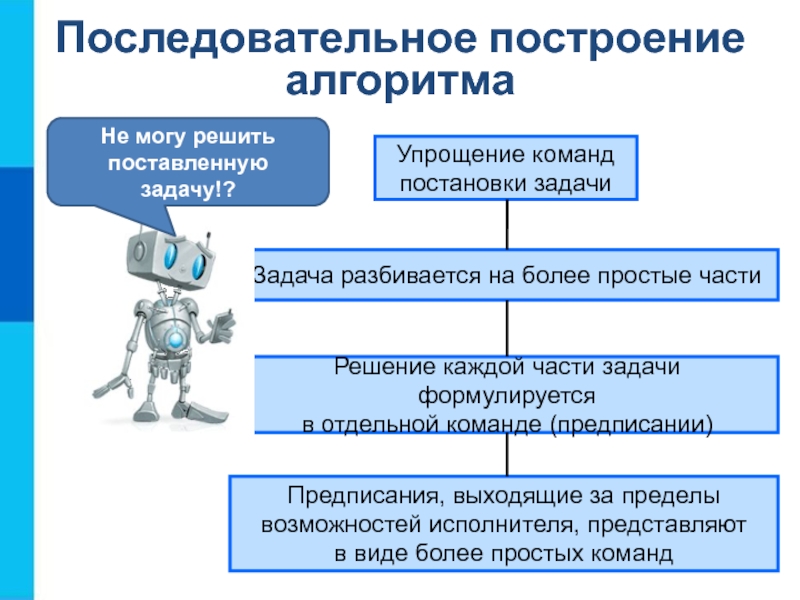
Упрощение команд
постановки задачи
Задача разбивается на более простые части
Решение
каждой части задачи формулируется
в отдельной команде (предписании)
Предписания, выходящие за пределы
возможностей
исполнителя, представляют в виде более простых команд
Не могу решить поставленную задачу!?
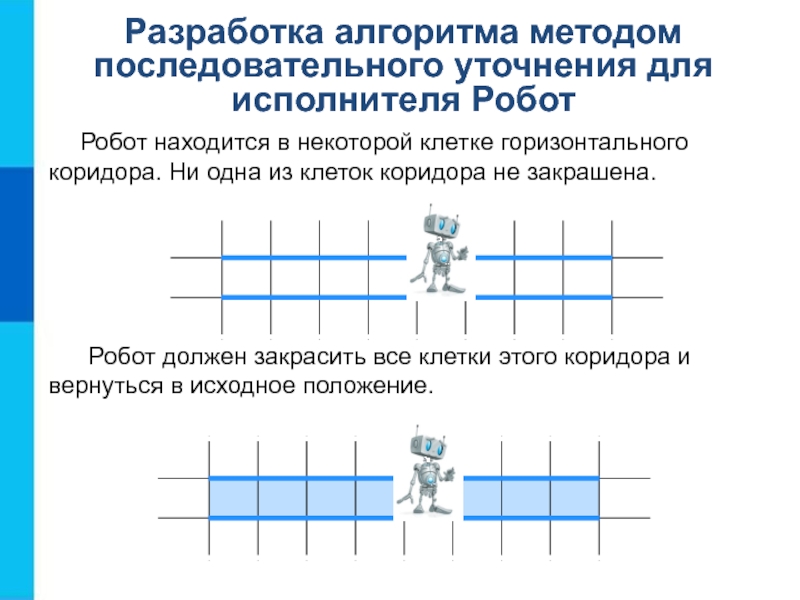
Слайд 5Разработка алгоритма методом последовательного уточнения для исполнителя Робот
Робот находится
в некоторой клетке горизонтального коридора. Ни одна из клеток коридора
не закрашена.Робот должен закрасить все клетки этого коридора и вернуться в исходное положение.
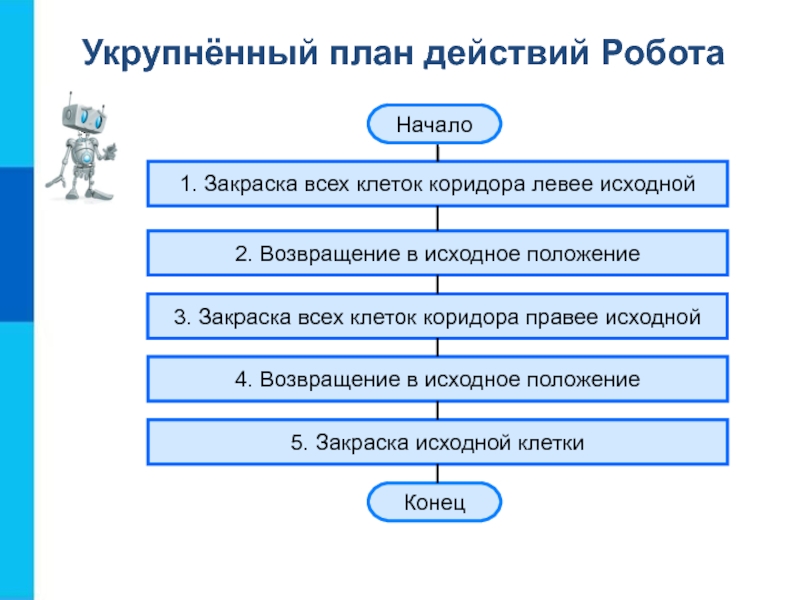
Слайд 6Укрупнённый план действий Робота
1. Закраска всех клеток коридора левее
исходной
2. Возвращение в исходное положение
3. Закраска всех клеток коридора правее
исходной4. Возвращение в исходное положение
5. Закраска исходной клетки
Начало
Конец
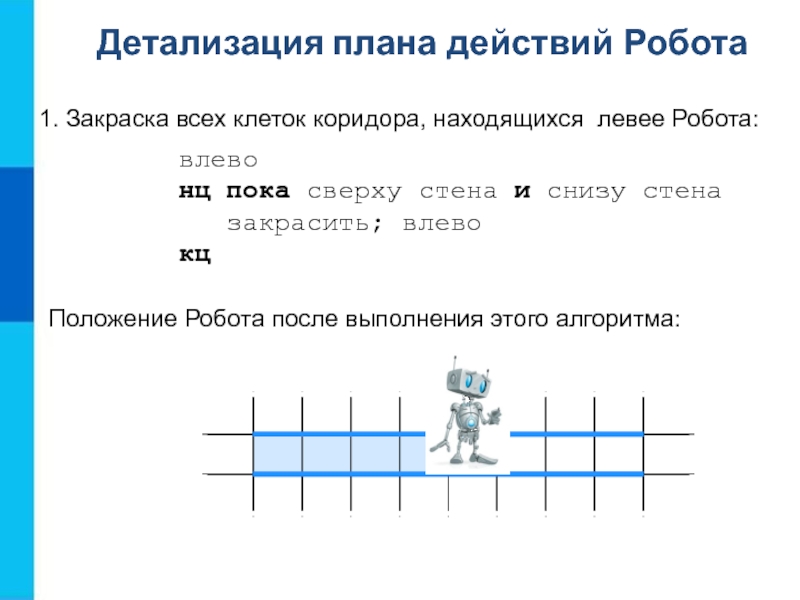
Слайд 71. Закраска всех клеток коридора, находящихся левее Робота:
Детализация плана действий
Робота
влево
нц пока сверху стена и снизу стена
закрасить; влево
кц
Положение
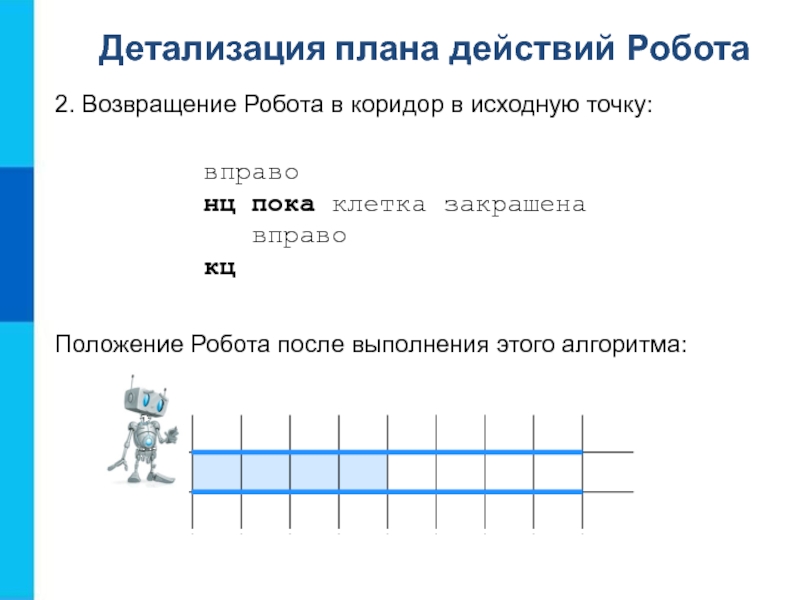
Робота после выполнения этого алгоритма:Слайд 82. Возвращение Робота в коридор в исходную точку:
вправо
нц пока
клетка закрашена
вправо
кц
Детализация плана действий Робота
Положение Робота после выполнения
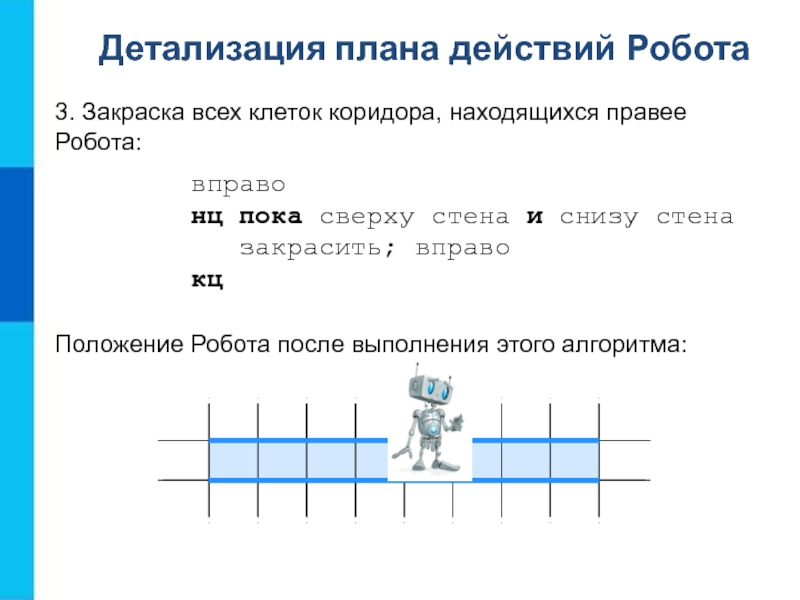
этого алгоритма:Слайд 93. Закраска всех клеток коридора, находящихся правее Робота:
вправо
нц пока сверху
стена и снизу стена
закрасить; вправо
кц
Детализация плана действий Робота
Положение
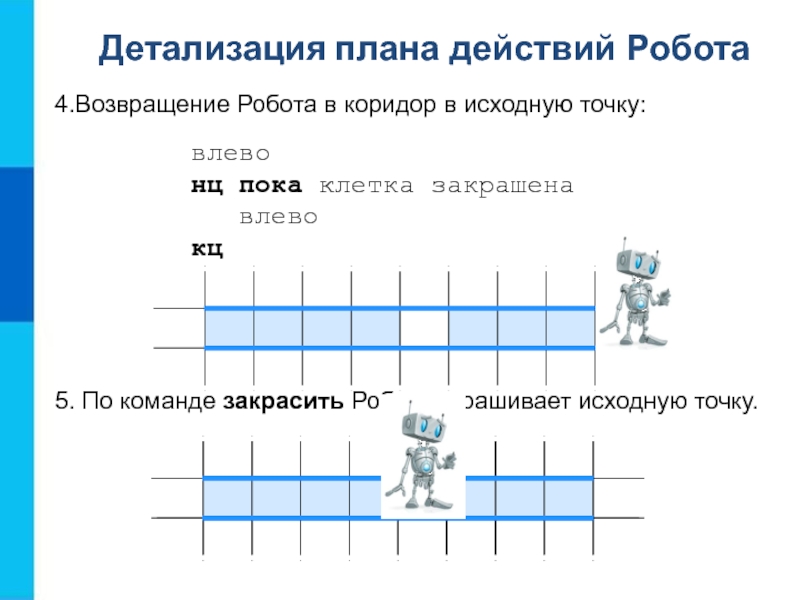
Робота после выполнения этого алгоритма:Слайд 104.Возвращение Робота в коридор в исходную точку:
влево
нц пока клетка
закрашена
влево
кц
5. По команде закрасить Робот закрашивает исходную точку.
Детализация плана действий Робота
Слайд 11алг
нач
влево
нц пока сверху стена и снизу
стена
закрасить; влево
кц
вправо
нц
пока клетка закрашенавправо
кц
вправо
нц пока сверху стена и снизу стена
закрасить; вправо
кц
влево
нц пока клетка закрашена
влево
кц
закрасить
кон
Программа для Робота
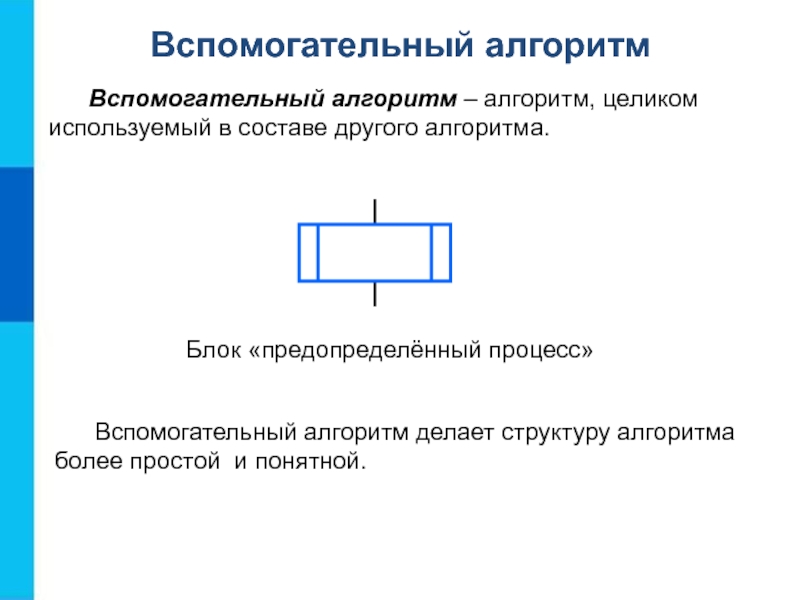
Слайд 12Вспомогательный алгоритм
Вспомогательный алгоритм – алгоритм, целиком используемый в составе
другого алгоритма.
Блок «предопределённый процесс»
Вспомогательный алгоритм делает структуру алгоритма более простой
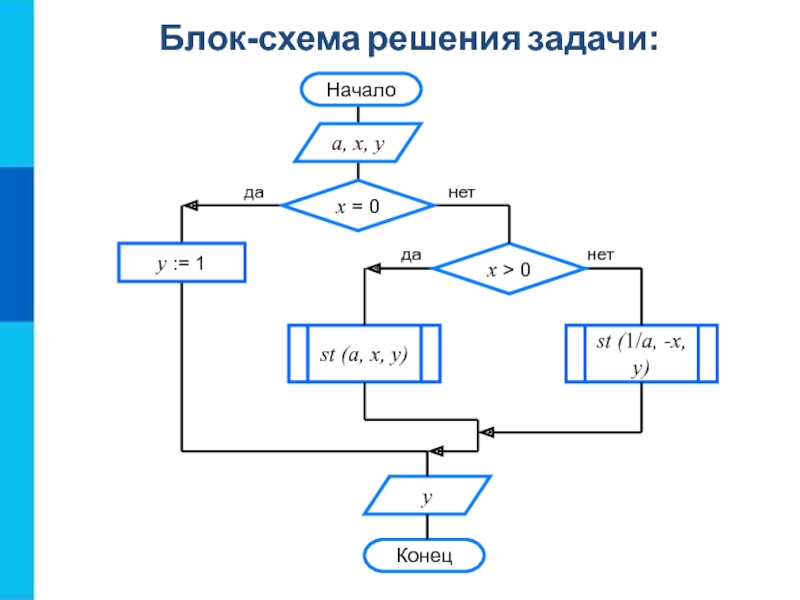
и понятной.Слайд 13Алгоритм вычисления степени
y = ax, где x – целое
число, a ≠ 0.
1,
при x = 0y = ax, при x >0,
, при x <0.
Обозначим алгоритм возведения числа в степень st(a, n, y).
Это вспомогательный алгоритм.
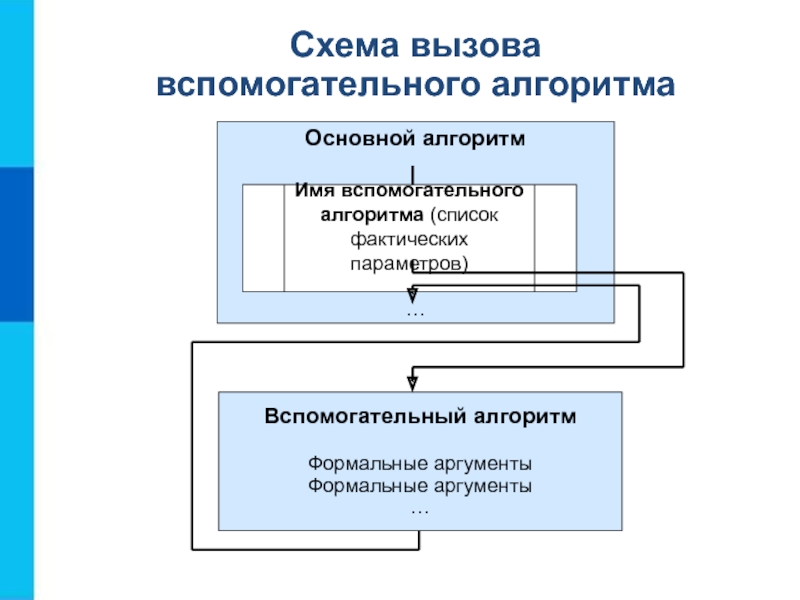
Слайд 15Формальные параметры используются при описании алгоритма.
Фактические параметры – те
величины, для которых будет исполнен вспомогательный алгоритм.
Типы, количество и
порядок следования формальных и фактических параметров должны совпадать.Формальные и фактические параметры
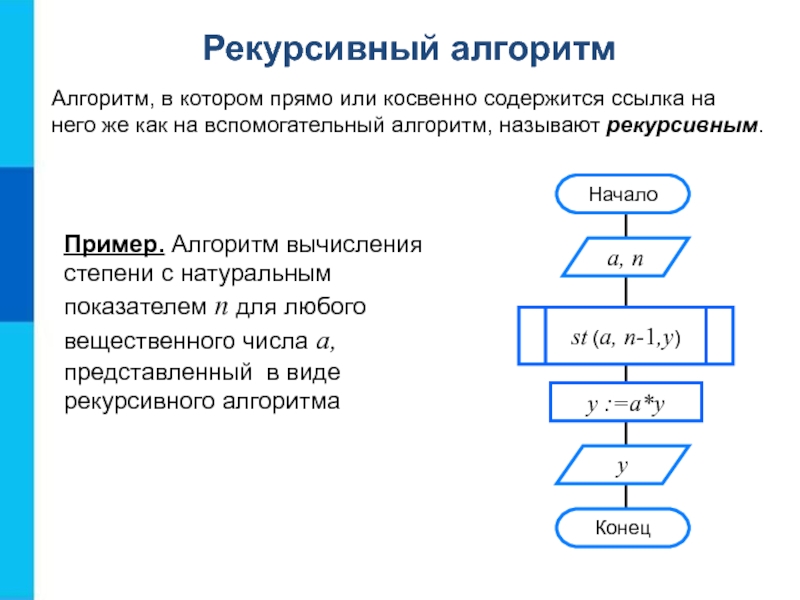
Слайд 17Пример. Алгоритм вычисления степени с натуральным показателем n для любого
вещественного числа а, представленный в виде рекурсивного алгоритма
Рекурсивный алгоритм
Алгоритм, в
котором прямо или косвенно содержится ссылка на него же как на вспомогательный алгоритм, называют рекурсивным.Слайд 18Снежинка Коха
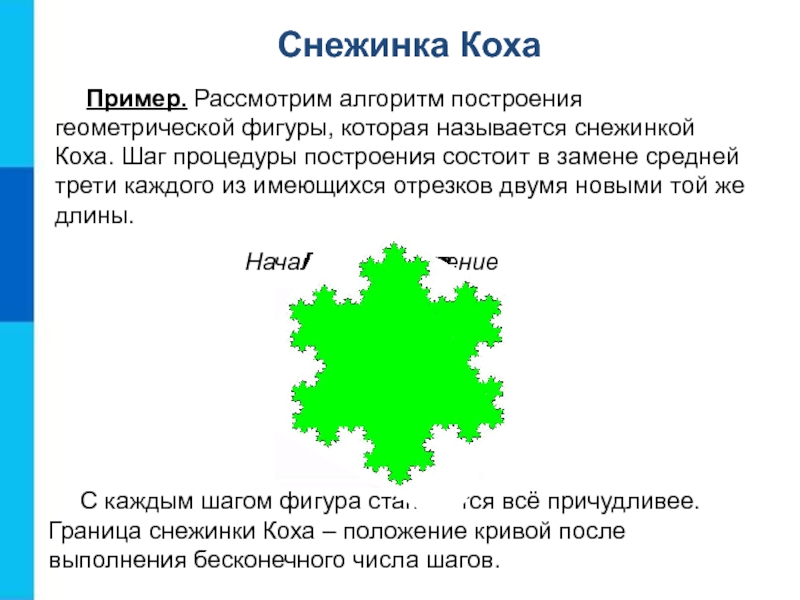
Пример. Рассмотрим алгоритм построения геометрической фигуры, которая называется снежинкой
Коха. Шаг процедуры построения состоит в замене средней трети каждого
из имеющихся отрезков двумя новыми той же длины.С каждым шагом фигура становится всё причудливее. Граница снежинки Коха – положение кривой после выполнения бесконечного числа шагов.
Начальное положение
Первый шаг
Второй шаг
Третий шаг
Слайд 19Самое главное
Метод последовательного построения алгоритма:
исходная задача разбивается на несколько
частей, каждая из которых проще всей задачи, и решение каждой
части формулируется в отдельной команде;если получаются команды, выходящие за пределы возможностей исполнителя, то они представляются в виде совокупности ещё более простых предписаний;
процесс продолжается до тех пор, пока все предписания не будут понятны исполнителю.
Вспомогательный алгоритм – алгоритм, целиком используемый в составе другого алгоритма.
Алгоритм, в котором прямо или косвенно содержится ссылка на него же как на вспомогательный алгоритм, называют рекурсивным.
Слайд 20Вопросы и задания
4. Известен рост каждого из N учеников 9А
класса и М учеников 9Б класса.
Опишите укрупнёнными блоками алгоритм
сравнения среднего роста учеников этих классов.3. Какая связь между методом последовательного построения алгоритма и такими процессами, как написание сочинения или подготовка к многодневному туристическому походу?
2. В чём заключается метод последовательного уточнения при построении алгоритма?
1. Почему при решении сложной задачи затруднительно сразу конкретизировать все необходимые действия?
Слайд 21Вопросы и задания
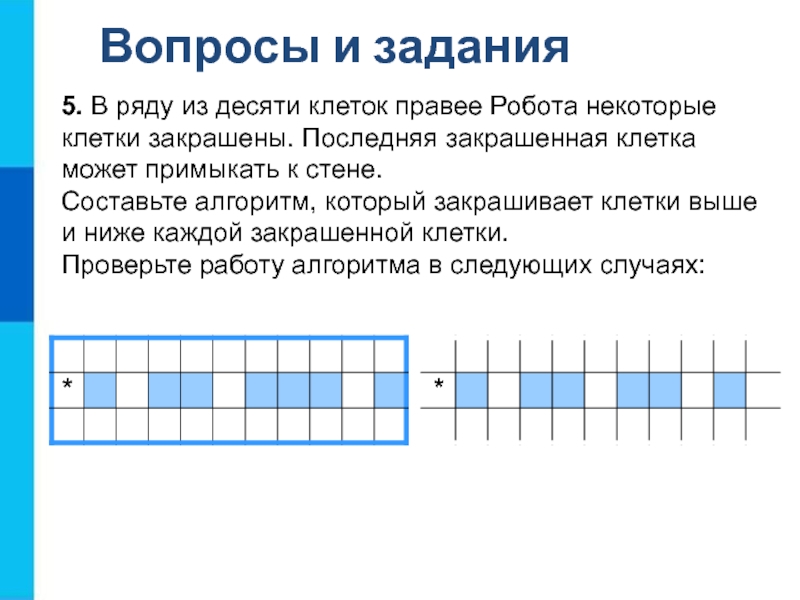
5. В ряду из десяти клеток правее Робота
некоторые клетки закрашены. Последняя закрашенная клетка может примыкать к стене.
Составьте алгоритм, который закрашивает клетки выше и ниже каждой закрашенной клетки.
Проверьте работу алгоритма в следующих случаях:
Слайд 22Вопросы и задания
9. Какие алгоритмы называют рекурсивными?
Приведите пример рекурсии из
жизни.
8. Сталкивались ли вы с идеей формальных и фактических параметров
при изучении математики и физики?Приведите пример.
7. Опишите процесс выполнения команды вызова вспомогательного алгоритма в основном алгоритме.
6. Для чего нужны вспомогательные алгоритмы?
Слайд 23Вопросы и задания
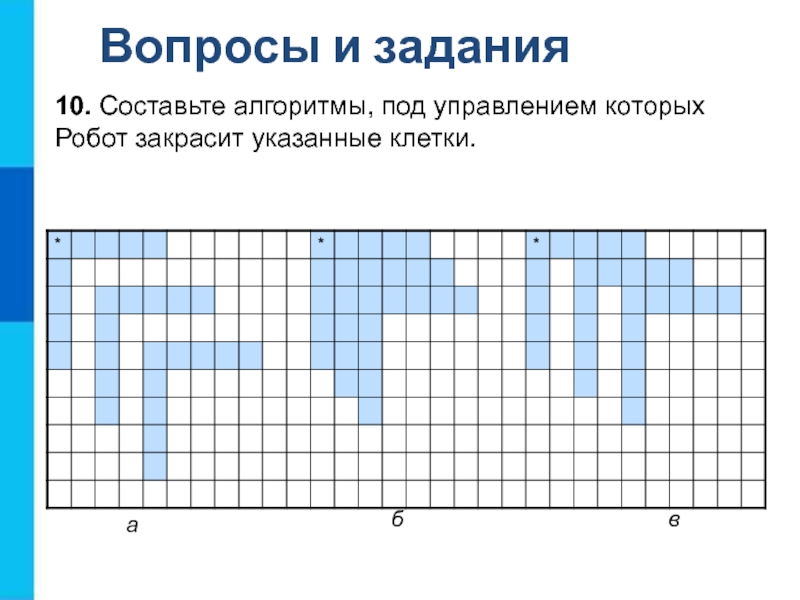
а
б
в
10. Составьте алгоритмы, под управлением которых Робот закрасит
указанные клетки.
Слайд 24Опорный конспект
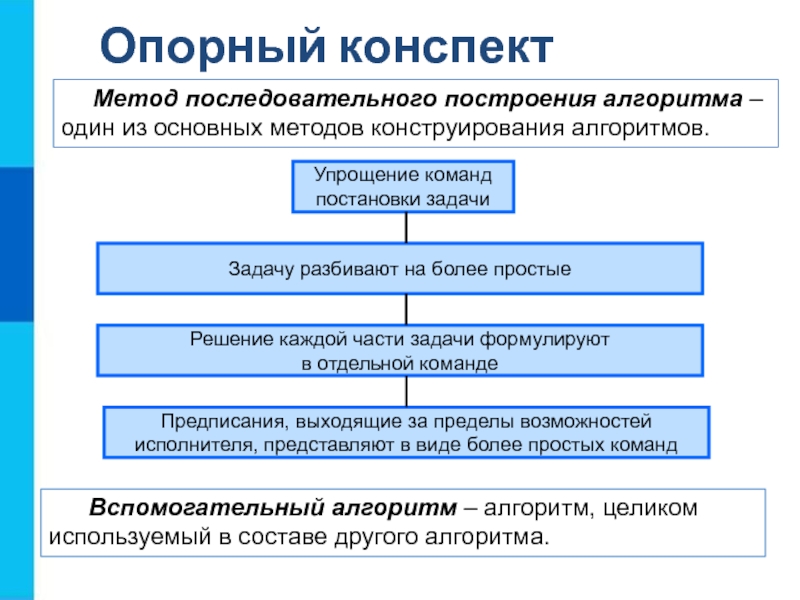
Метод последовательного построения алгоритма – один из основных методов
конструирования алгоритмов.
Упрощение команд
постановки задачи
Задачу разбивают на более простые
Решение каждой части
задачи формулируютв отдельной команде
Предписания, выходящие за пределы возможностей
исполнителя, представляют в виде более простых команд
Вспомогательный алгоритм – алгоритм, целиком используемый в составе другого алгоритма.