Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Координаты вектора в пространстве
Содержание
- 1. Координаты вектора в пространстве
- 2. Цели обучения:10.4.5 - уметь находить координаты и длину вектора в пространстве
- 3. Критерии оценивания– умеет находить координаты вектора в
- 4. Актуализация изученного материалаОпределение вектора в пространствеЧто называют
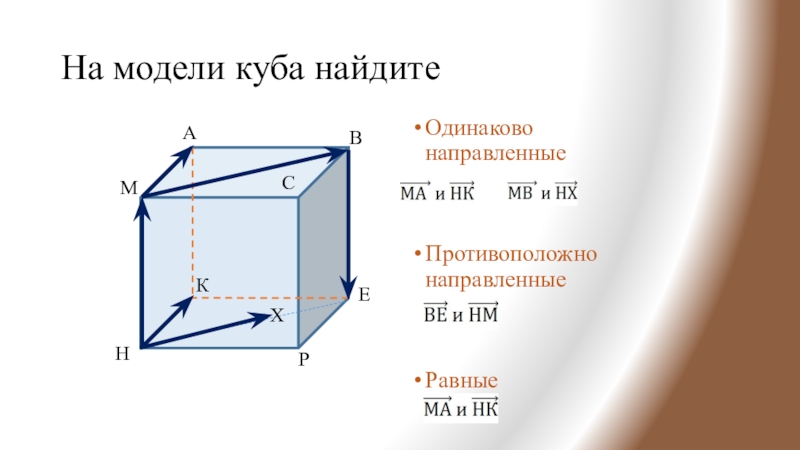
- 5. Одинаково направленныеПротивоположно направленныеРавные На модели куба найдитеХ
- 6. ОпределениеВеличины, которые характеризуются, не только числом, но
- 7. Определение
- 8. Front work Дескрипторы- записывает разложение векторов по координатным векторам;- определяет координаты векторов.
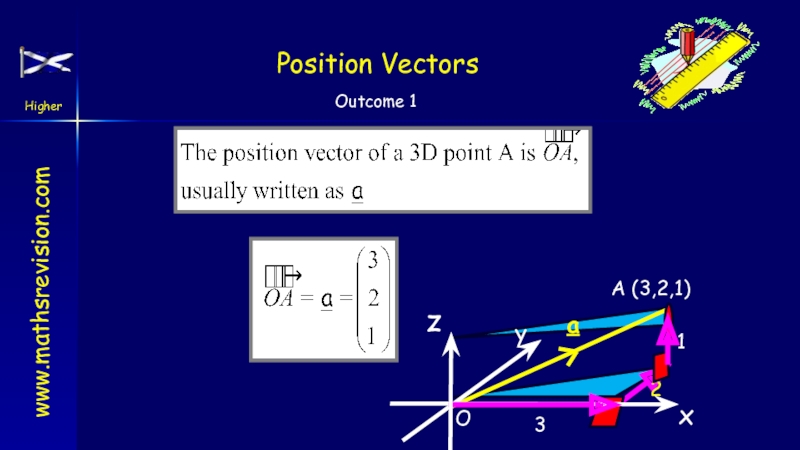
- 9. Position Vectorsza231xyA (3,2,1)
- 10. Координаты вектораА(х1;у1;z1) B(x2;y2;z2) (x2-х1;y2-у1;z2-z1)Пример:определить
- 11. Равные векторыАВРавные векторы имеют равные соответствующие координаты
- 12. Front work Дано: А(2;7;-3); В(1;0;3); С(-3;-4;5); М(-2;3;-1)
- 13. Длина вектораФормула:
- 14. Определить длину если М(9;3;-6) и С(-5; 4;-1)
- 15. ОРТ вектораОртом данного вектора называется вектор, который
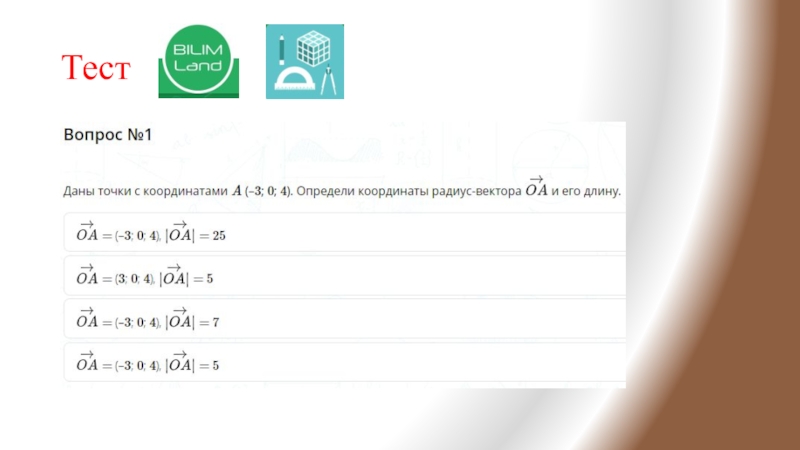
- 16. Тест
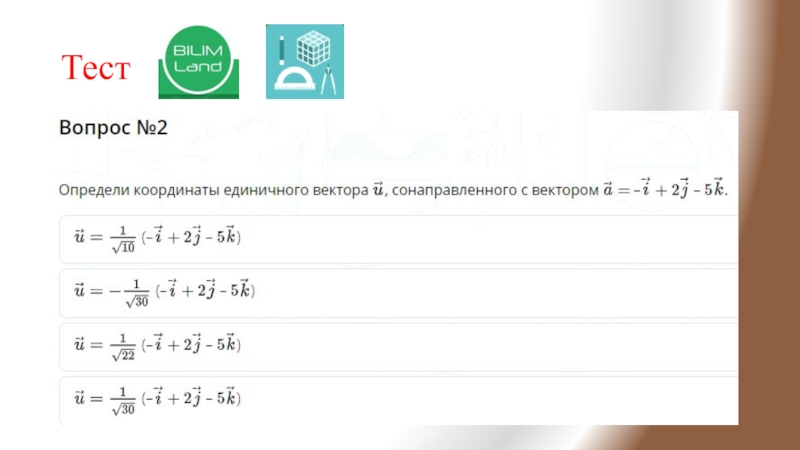
- 17. Тест
- 18. Тест
- 19. Тест
- 20. Дескрипторы;- использует формулу нахождения координат вектора;- использует
- 21. Скачать презентанцию
Цели обучения:10.4.5 - уметь находить координаты и длину вектора в пространстве
Слайды и текст этой презентации
Слайд 3Критерии оценивания
– умеет находить координаты вектора в пространстве;
– умеет решать
задачи с использованием координат векторов;
–– знает различные обозначения для векторов
в пространстве;– знает формулу длины вектора в пространстве;
– умеет вычислять длину вектора в пространстве;
Слайд 4Актуализация изученного материала
Определение вектора в пространстве
Что называют модулем вектора?
Какие векторы
называют равными?
Чем характеризуется вектор?
Что такое единичный вектор?
Слайд 6Определение
Величины, которые характеризуются, не только числом, но еще и направлением,
называются векторными величинами, или просто векторами.
Векторами являются, например, скорость, ускорение, сила.
Геометрически
векторы изображаются направленными отрезками.Определение. Направленный отрезок называется вектором.
Вектор характеризуется следующими элементами:
начальной точкой;
направлением;
длиной («модулем вектора»).
Длиной вектора называется расстояние между его начальной и конечной точками.
Слайд 8Front work
Дескрипторы
- записывает разложение векторов по координатным векторам;
- определяет
координаты векторов.
Слайд 10Координаты вектора
А(х1;у1;z1) B(x2;y2;z2)
(x2-х1;y2-у1;z2-z1)
Пример:
определить координаты
,
если М(9;3;-6) и С(-5; 4;-1)
(-5-9; 4-3; -1-(-6))(-14;1;5)
Координаты вектора в пространстве
А
В
Слайд 11Равные векторы
А
В
Равные векторы имеют равные соответствующие координаты
(х;y;z) (a;b;c)
Если х=а,у=b, z=с, то
=С
М
Слайд 12Front work
Дано: А(2;7;-3); В(1;0;3); С(-3;-4;5); М(-2;3;-1)
Определить: пары
равных векторов
Решение:
Равны соответствующие координаты у
векторов
, , значит, они попарно равны
Слайд 14Определить длину
если М(9;3;-6) и С(-5; 4;-1)
(-5-9; 4-3; -1-(-6))
(-14;1;5)
| |=?
Front work
Слайд 15ОРТ вектора
Ортом данного вектора называется вектор, который сонаправлен с данным
вектором и имеет модуль, равный единице.
Слайд 20
Дескрипторы;
- использует формулу нахождения координат вектора;
- использует формулу нахождения длины
вектора;
- находит длины векторов;
- определяет вид треугольника.
