Корреляционный анализ

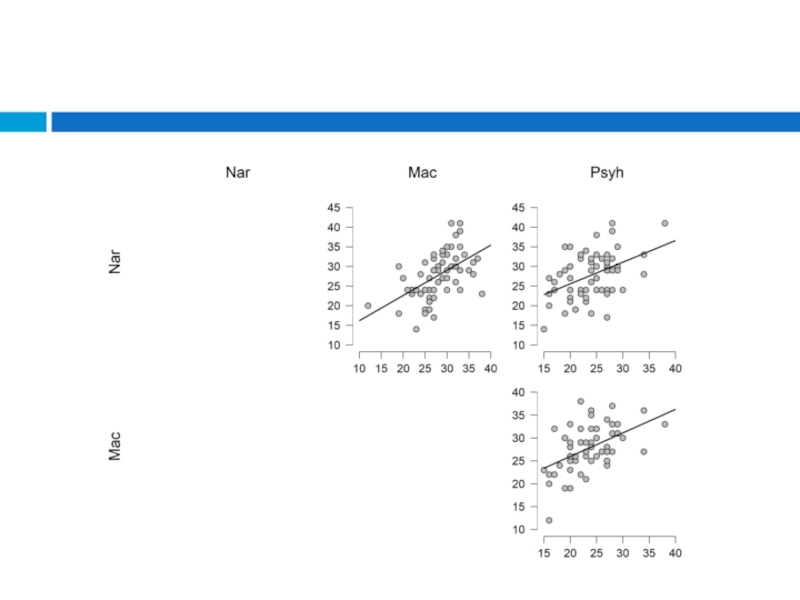
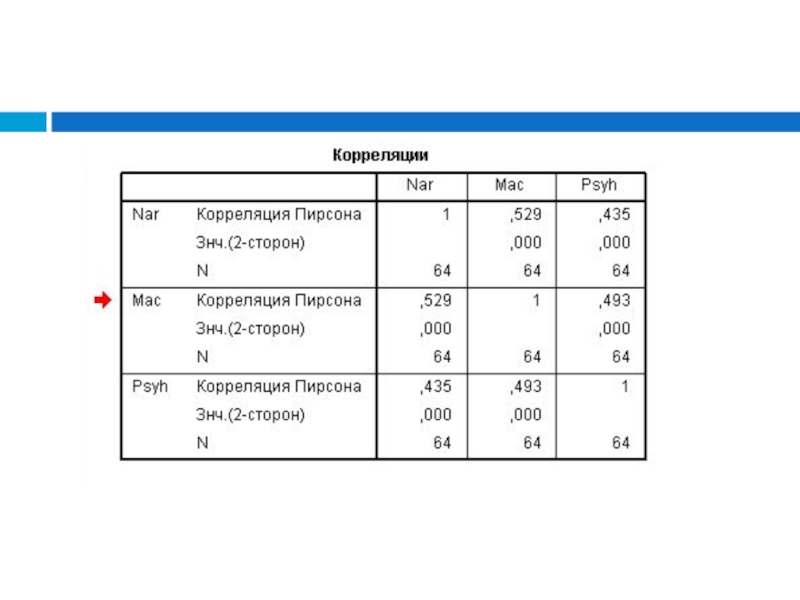
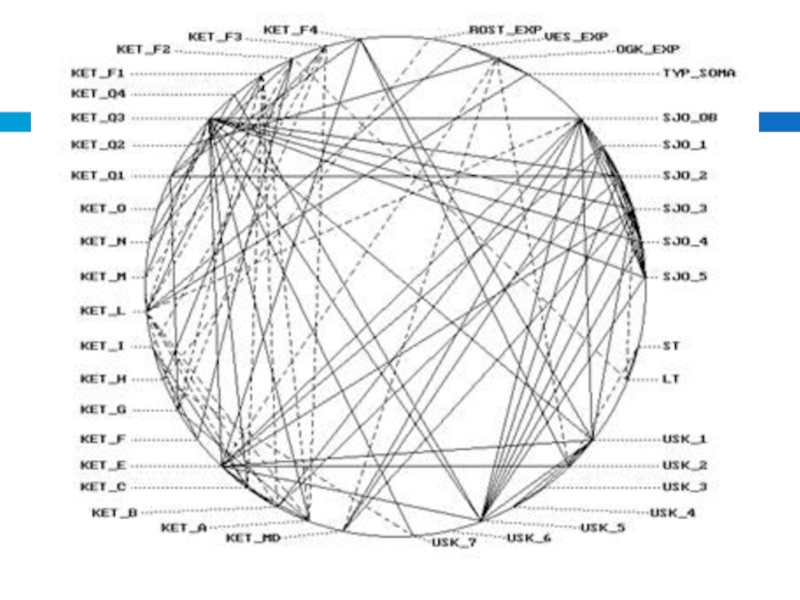
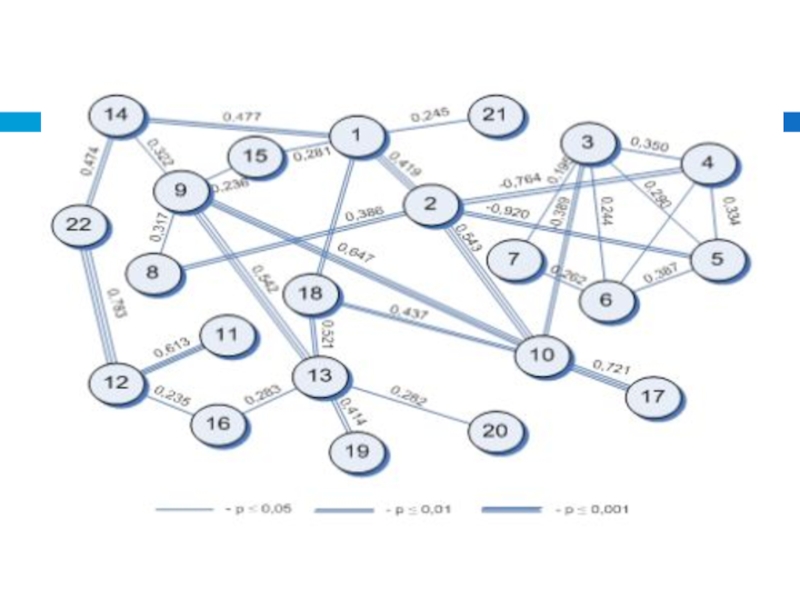
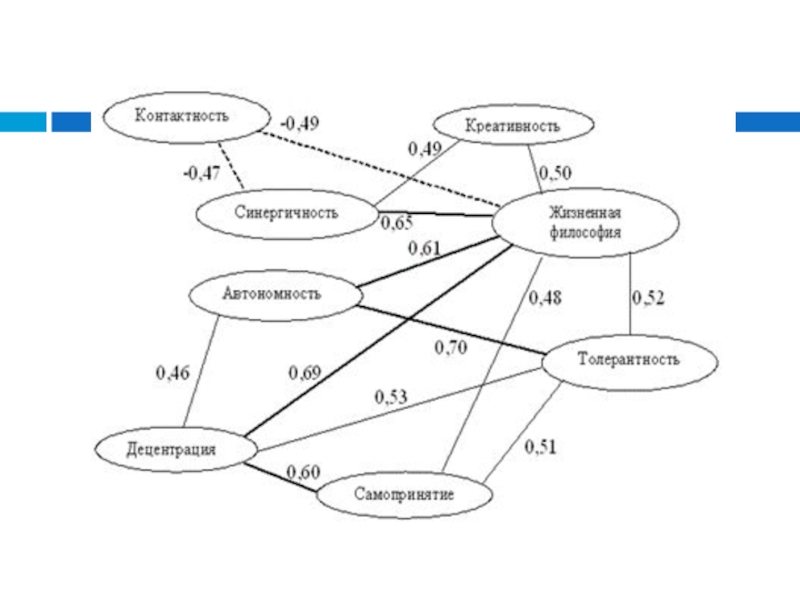
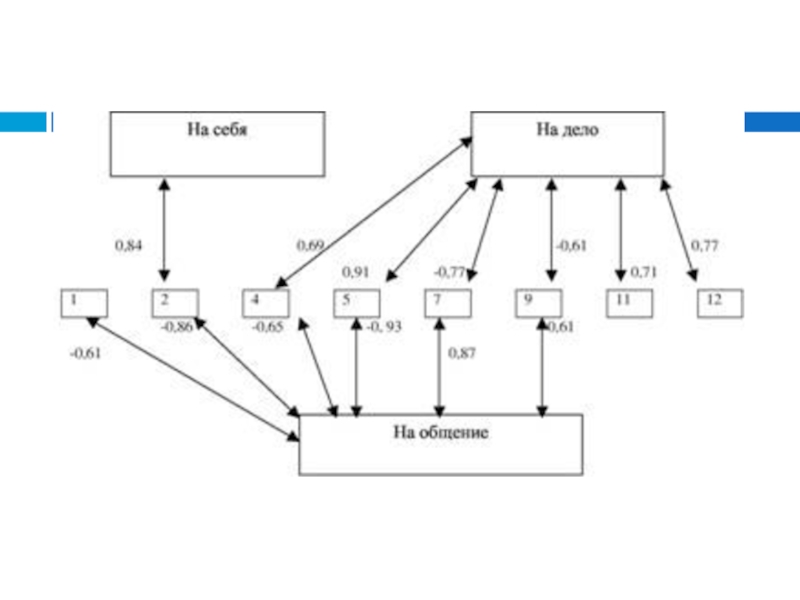
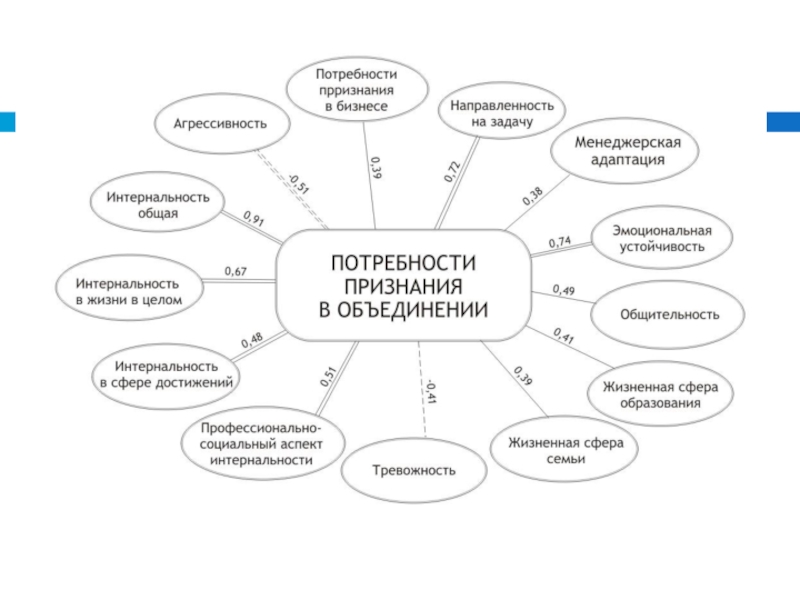
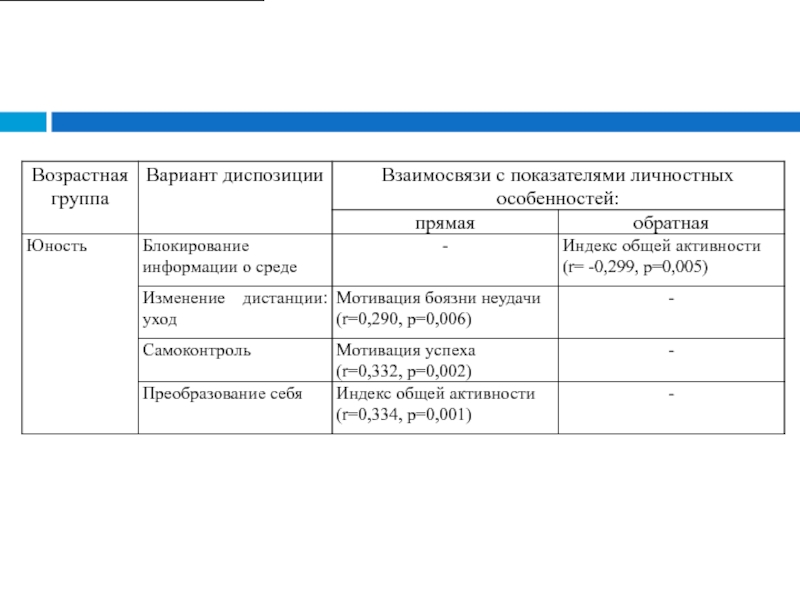
мера взаимосвязи (совместной изменчивости) двух переменных.

Автор термина и основоположник корреляционного

анализа – Френсис Гальтон.
Наиболее распространенные коэффициенты корреляции разработал Карл Пирсон.

увеличением или уменьшением одной переменной Х, вторая переменная Y в

среднем либо также растет, либо убывает.

Нелинейная корреляция – при увеличении одной величины, характер изменения второй не линеен, а описывается другими законами.

вероятностной взаимосвязи переменных; принимает значения в диапазоне от –1 до

+ 1.

Сила связи достигает максимума при условии взаимно однозначного соответствия. Показателем силы связи является абсолютная (без учета знака) величина коэффициента корреляции.

Направление связи определяется прямым или обратным соотношением значений двух переменных. Показателем направления связи является знак коэффициента корреляции.

увеличением переменной Х переменная Y в среднем также увеличивается.

Отрицательная корреляция

– если с увеличением переменной Х переменная Y в среднем имеет тенденцию к уменьшению.

степени влияют на корреляцию Пирсона, т.к. величина этого коэффициента прямо

пропорциональна отклонению значения переменной от среднего.

Влияние «третьей» переменной – корреляция между двумя переменными обусловлена не связью между соответствующими свойствами, а влиянием некоторой общей причины совместной изменчивости этих переменных (например: обратная связь роста и длины волос, третья переменная – пол).

Нелинейные связи – при уменьшении или увеличении значений одной из переменной связь меняет свое направление (например: связь активации и продуктивности деятельности). В подобных случаях выборку разделяют на подгруппы.

криволинейным связям.

Условия применения:
Сравниваемые переменные должны быть получены в интервальной шкале

или шкале отношений.
Распределения переменных должны быть близки к нормальному.
Число варьирующих признаков в сравниваемых переменных должно быть одинаковым.
Таблицы уровней значимости рассчитаны от 5 до 1000 человек. Оценка уровня значимости осуществляется при числе степеней свободы k= n-2
Выборка должна составлять от 30 респондентов

непараметрическим показателям связи между переменными, измеренными в ранговой шкале.

Условия применения:
Сравниваемые

переменные должны быть получены в порядковой (ранговой) шкале, но могут быть также измерены в шкале интервалов и отношений.
Характер распределения не имеет значения.
Число варьирующих признаков в сравниваемых переменных должно быть одинаковым.
Таблицы для определения критических значений рас читаны от 5 до 40 человек, при большем числе используются таблицы Пирсона. Нахождение критических значений осуществляется при k=n.
Выборка от 5 человек и более.

из множества Р переменных, измеренных в количественной шкале на одной

выборке.

Основные характеристики корреляционной матрицы:
она является квадратной;
она симметрична относительно главной диагонали;
на главной диагонали располагаются единицы, т.к. корреляция признака с самим собой равна единице.

визуальный анализ корреляционных плеяд – графического изображения структуры статистически значимых

связей.

- среднезначимая положительная взаимо-связь (р≤0,05)
____ высокозначимая отрицательная взаимо-связь (р≤0,01)
- -

- - - - - среднезначимая отрицательная взаимо-связь (р≤0,05)

Данные связи ожидаемы, так как подтверждают внутреннюю согласованность и валидность

теста.

Межкорреляционные взаимосвязи – связи между показателями разных методик. Это основная задача данного вида математической процедуры.