Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Кратчайшие пути в графе
Содержание
- 1. Кратчайшие пути в графе
- 2. 28.04.2014Кратчайшие пути 1Кратчайшие пути в графеПуть p
- 3. 28.04.2014Кратчайшие пути 1Вычисление расстояний и нахождение путейПусть
- 4. 28.04.2014Кратчайшие пути 1Пример2 – вес ребра w(i, j) [1] – расстояние d(u,v)[8] = 4 + [4]
- 5. 28.04.2014Кратчайшие пути 1Пример[4] = − 4 + [8][8] = 5 + [3][3] = 3 + [0]
- 6. 28.04.2014Кратчайшие пути 1Алгоритм нахождения кратчайшего пути
- 7. 28.04.2014Кратчайшие пути 1Алгоритм нахождения кратчайшего пути
- 8. 28.04.2014Кратчайшие пути 1Задачи вычисления длин кратчайших путей
- 9. 28.04.2014Кратчайшие пути 1Задачи вычисления расстояний от фиксированной
- 10. 28.04.2014Кратчайшие пути 1Релаксация (ослабление) ребра u →
- 11. 28.04.2014Кратчайшие пути 1Релаксация входящих ребер относительно вершины
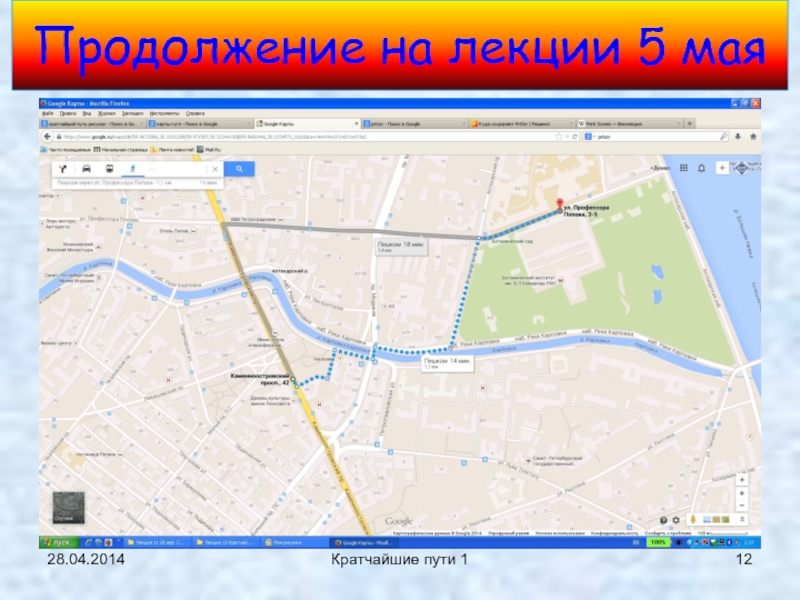
- 12. Продолжение на лекции 5 мая28.04.2014Кратчайшие пути 1
- 13. 28.04.2014Кратчайшие пути 1
- 14. Алгоритм Дейкстры (Dijkstra E.W. - 1959)28.04.2014Кратчайшие пути 1
- 15. 28.04.2014Кратчайшие пути 1Алгоритм ДейкстрыW [ *, *
- 16. 28.04.2014Кратчайшие пути 1for (∀ v ∈V) DL[v]
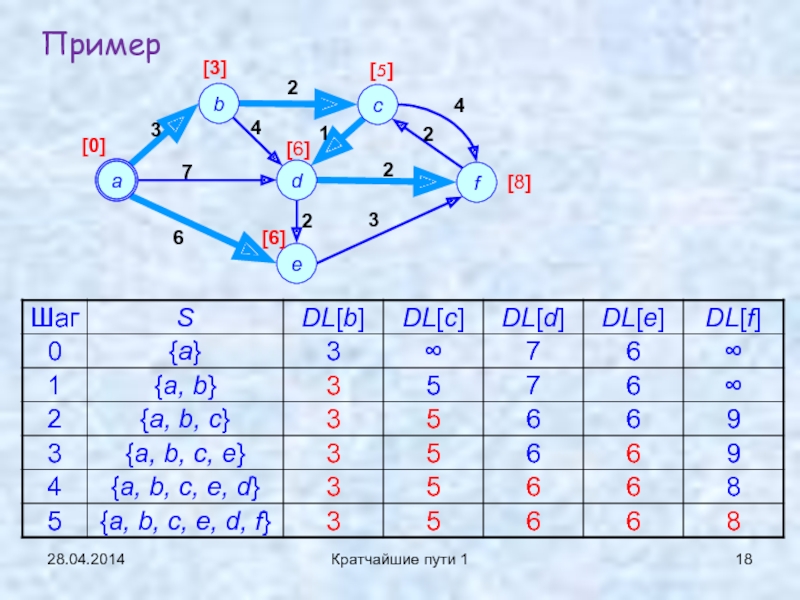
- 17. 28.04.2014Кратчайшие пути 1Пример
- 18. 28.04.2014Кратчайшие пути 1Пример
- 19. 28.04.2014Кратчайшие пути 1Корректность алгоритма: см. инвариант цикла
- 20. 28.04.2014Кратчайшие пути 11) Множество T представляется пирамидой
- 21. СледующийАлгоритм Форда-Беллмана 28.04.2014Кратчайшие пути 1
- 22. 28.04.2014Кратчайшие пути 1Алгоритм Форда-Беллмана нахождения расстояний от
- 23. 028.04.2014Кратчайшие пути 1Алгоритм Форда-БеллманаПример непригодности алгоритма Дейкстры
- 24. 28.04.2014Кратчайшие пути 1for (∀ v ∈ V)
- 25. 28.04.2014Кратчайшие пути 1Вариант сложности O (nm)for (∀ v ∈ V) DL[v]=W[s,v]; DL[s] =0;for (k=1; k
- 26. 28.04.2014Кратчайшие пути 1Пример. n = 6 Шаг 0
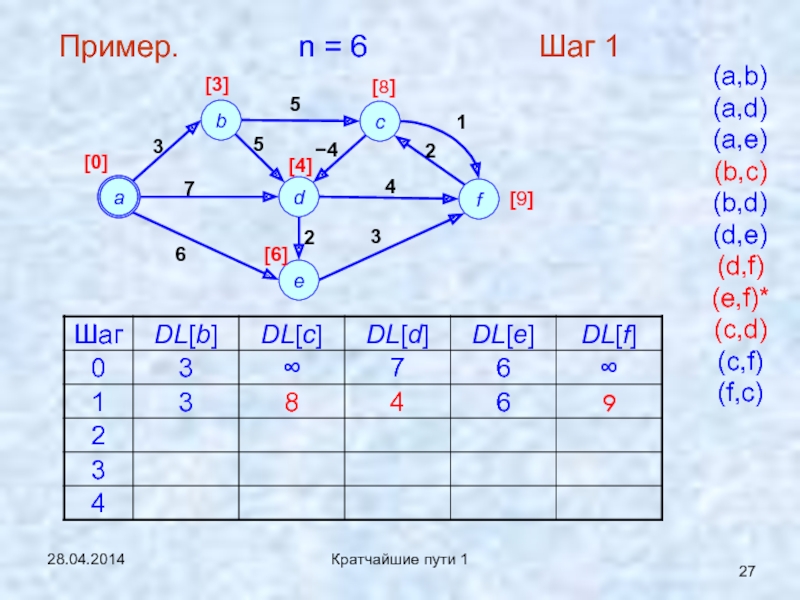
- 27. 28.04.2014Кратчайшие пути 1Пример. n = 6 Шаг 1(a,b)(a,d)(a,e)(b,c)(b,d)(d,e)(d,f)(e,f)*(c,d)(c,f)(f,c)
- 28. 28.04.2014Кратчайшие пути 1Пример. n = 6 Шаг 2(a,b)(a,d)(a,e)(b,c)(b,d)(d,e)(d,f)(e,f)(c,d)(c,f)(f,c)
- 29. 28.04.2014Кратчайшие пути 1Пример. n = 6 Шаг 3(a,b)(a,d)(a,e)(b,c)(b,d)(d,e)(d,f)(e,f)(c,d)(c,f)(f,c)
- 30. 28.04.2014Кратчайшие пути 1Индуктивное утверждение (“инвариант”) цикла for (k=1; k
- 31. 28.04.2014Кратчайшие пути 1 Если P( [1..k) )
- 32. 28.04.2014Кратчайшие пути 1После очередной итерацииd(s,v) ≤ DL[v]
- 33. 28.04.2014Кратчайшие пути 1Кратчайшие пути между всеми парами вершинСм. лекцию 12
- 34. Примечание 28.04.2014Кратчайшие пути 1
- 35. 28.04.2014Кратчайшие пути 1КОНЕЦ ЛЕКЦИИКОНЕЦ ЛЕКЦИИКОНЕЦ
- 36. Скачать презентанцию
Слайды и текст этой презентации
Слайд 128.04.2014
Кратчайшие пути 1
Лекция 11.2
Раздел: Алгоритмы на графах
Тема лекции:
Кратчайшие пути
в графе
Слайд 228.04.2014
Кратчайшие пути 1
Кратчайшие пути в графе
Путь p в графе G
= (V, E):
p: u ⇒ v ≡ u
= u1 → u2 → u3 → … → uk = vВзвешенный граф G = (V, E, W),
где w(i, j) = w(vi, vj) - произвольны.
Длина пути:
p: u ⇒ v, p ∈ P(u, v) – множество путей между u и v
Приложения… W(u, v) = − log2 Prob(u, v)
Слайд 328.04.2014
Кратчайшие пути 1
Вычисление расстояний и нахождение путей
Пусть вычислены все расстояния
d (u, v),
в т.ч. d (s, t).
Как найти
путь p: s ⇒ t ? u
d (s, t) = d (s, u) + w (u, t)
Часть кратчайшего пути тоже кратчайший путь! v1~>vi~>vj~>vk (1 ≤ i ≤ j ≤ k)
Слайд 628.04.2014
Кратчайшие пути 1
Алгоритм нахождения кратчайшего пути
по расстояниям между вершинами
/*Дано:
s, t – фиксированные вершины; s, t ∈V;
DL [ *
] – расстояния от вершины s до каждой вершины графа; DL[v]=d(s,v);W[u, v] – матрица весов ребер, u, v ∈V;
Результат: St – стек, содержащий кратчайший путь от s до t,
т.е. последовательность вершин s=v0, v1, … , vk=t
*/
Create(st); st ← t; v = t;
while (v != s) {
u = вершина, для которой DL[v]=DL[u]+W[u,v];
St ← u;
v=u;
}
Слайд 728.04.2014
Кратчайшие пути 1
Алгоритм нахождения кратчайшего пути
продолжение
Детализация строки
u = вершина,
для которой DL[v]=DL[u]+W[u,v];
Встать в начало Adj_In[v];
do
u = очередной элемент
из Adj_In[v];while (d (s, t) != d (s, u) + w [ u, t ])
Adj_In[v] – список смежности входящих ребер
Adj_Out[v] – список смежности исходящих ребер
Adj_In[v]
Adj_Out[v]
Сложность
O(m)
Слайд 828.04.2014
Кратчайшие пути 1
Задачи вычисления длин кратчайших путей (расстояний)
Стартовая вершина s
фиксирована, конечная вершина t фиксирована. Найти d (s, t).
Стартовая вершина
s фиксирована. Найти d (s, v) для ∀ v ∈ V \ s.Найти d (s, t) : ∀ s, t ∈ V & (s ≠ t ). Т.е. найти расстояния между всеми парами вершин.
Замечание: неизвестен ни один алгоритм решения задачи 1, который был бы более эффективным, чем известные алгоритмы, решающие задачу 2
Слайд 928.04.2014
Кратчайшие пути 1
Задачи вычисления расстояний от фиксированной вершины
Общая схема большинства
алгоритмов:
рассматриваются временные пометки вершин dl [v], которые являются верхними
ограничениями для расстояний: dl [v] ≥ d (s, v) .Улучшение оценки dl [v]:
void Relax (vert u, vert v)
// релаксация (ослабление) ребра u → v
{ if (dl [v] > dl [u] + W [ u, v ] ) dl [v] = dl [u] + W [ u, v ];
} //Relax
т.е. dl [v] := min (dl [v], dl [u] + W [ u, v ])
Слайд 1028.04.2014
Кратчайшие пути 1
Релаксация (ослабление) ребра u → v
1
dl [u]
dl [v]
w
[u,v]
dl [u]
dl [v]
w [u,v]
Relax (u, v);
for (∀u ∈ Adj_In[v]) Relax(u,
v);dl [a]
dl [b]
w [b,v]
w [a,v]
Релаксация входящих ребер относительно вершины v
Слайд 1128.04.2014
Кратчайшие пути 1
Релаксация входящих ребер относительно вершины v :
for (∀u
∈ Adj_In[v]) Relax(u, v);
В результате
dl [v] = min (
dl [u] + W [ u, v ] ⎢ ∀u ∈ Adj_In[v] )Инициализация: dl [v] = W [ s, v ] или dl [v] = ∞, dl [s] = 0.
Утверждение 1.
Если dl [v] = d (s, v), то релаксация не изменит dl [v] .
Утверждение 2.
Если u лежит на кратчайшем пути s ⇒ v и dl [u] = d (s, u), то после Relax(u, v) будет dl [v] = d (s, v).
Задачи вычисления расстояний от фиксированной вершины
Слайд 1528.04.2014
Кратчайшие пути 1
Алгоритм Дейкстры
W [ *, * ] ≥ 0
Идея
алгоритма: V = S + T, S ∩ T=
∅Инвариант:
( ∀ v∈S : DL[v] = d(s,v) ) &
( ∀ v∈T : DL[v] = длина кратчайшего из тех путей из s в v, в которых все вершины, кроме v, принадлежат множеству S )
S
T
s
Вершина u с минимальной пометкой
S:=S+{u}; T:=T \ {u}
Слайд 1628.04.2014
Кратчайшие пути 1
for (∀ v ∈V) DL[v] =W[s,v];
DL[s] =0;
T
= V \ {s}; // S = {{s}}
while
(T ≠ ∅) {u = вершина x∈T, такая, что DL[x] = min { DL[p] : p ∈T };
T =T \ {u}; // S =S+{u}
for (∀ v ∈T) Relax (u,v);
} //while
Алгоритм Дейкстры
Дано: Орграф G= DL[v] = min { DL[v], DL[u]+W[u,v] }
W[u, v] – матрица весов дуг, u, v ∈V; W[u, v] ≥ 0
Результат: Расстояния от источника s до всех вершин графа DL[v]=d(s,v), v ∈V;
Слайд 1928.04.2014
Кратчайшие пути 1
Корректность алгоритма: см. инвариант цикла while;
от противного
Алгоритм
Дейкстры
T
s
u
u′
Пусть u = arg min { DL[p] : p ∈T
}; но DL[u] > d(s,u).Тогда ∃ u′ ∈T : DL[u′ ] = d(s,u′ ) ≤ d(s,u) < DL[u] !
(и u′ - первая вершина из T на пути s ⇒ u)
(противоречие) Сложность O (n 2)
Слайд 2028.04.2014
Кратчайшие пути 1
1) Множество T представляется
пирамидой Heap(T) с приоритетами
DL[v];
при этом Inv Heap(T): (∀u∈T:
(u=отец (v)) → (DL[u] ≤ DL[v]) ).Тогда min(T) – в корне Heap(T), и исключение u из T есть удаление корня Heap(T) с восстановлением пирамидальности.
2) Используются списки смежности AdjOut[*].
Тогда обновление DL[v] после выбора вершины u реализуется следующим образом:
for (∀v∈ AdjOut[u])
if (DL[u] + W[u,v] < DL[v]) {
DL[v] = DL[u]+W[u,v];
Восстановить пирамидальность Heap(T) вверх от узла v;
}
Алгоритм Дейкстры (модификация O(m log n) )
Вершина u с минимальной пометкой
Каждая дуга графа анализируется один раз (!) и может вызвать действие O(log n)
Слайд 2228.04.2014
Кратчайшие пути 1
Алгоритм Форда-Беллмана
нахождения расстояний от источника
до остальных
вершин в графе,
не содержащем контуров отрицательной длины
Дано:
Орграф G=
с выделенным источником s∈V; ⎢V ⎢= n ;W[u, v] – матрица весов дуг, u, v ∈V;
(граф не содержит контуров отрицательной длины)
Результат:
Расстояния от источника s до всех вершин графа
DL[v] = d(s,v), v ∈V;
Слайд 230
28.04.2014
Кратчайшие пути 1
Алгоритм Форда-Беллмана
Пример непригодности алгоритма Дейкстры при произвольных весах
b
2
1
Но
Relax (b, c) дает DL[c] = 0 !!!
Слайд 2428.04.2014
Кратчайшие пути 1
for (∀ v ∈ V) DL[v] =W[s,v];
DL[s] = 0;
for (k=1; k
for (∀ v ∈ V \ {s})
for (∀ u ∈ V) Relax (u, v);
Алгоритм Форда-Беллмана
DL[v] = min { DL[v], DL[u]+W[u,v] }
Сложность O (n 3)
Слайд 2528.04.2014
Кратчайшие пути 1
Вариант сложности O (nm)
for (∀ v ∈ V)
DL[v]=W[s,v];
DL[s] =0;
for (k=1; k
(∀ e ∈ E) Relax (u, v); //e=(u, v) Алгоритм Форда-Беллмана
Примечание: если ещё раз (дополнительно) выполнить тело цикла “for (k=1; …)” и проверить уменьшение в Relax, то можно обнаружить в графе цикл отрицательной длины (в обоих вариантах)
Слайд 2728.04.2014
Кратчайшие пути 1
Пример. n = 6
Шаг 1
(a,b)
(a,d)
(a,e)
(b,c)
(b,d)
(d,e)
(d,f)
(e,f)*
(c,d)
(c,f)
(f,c)
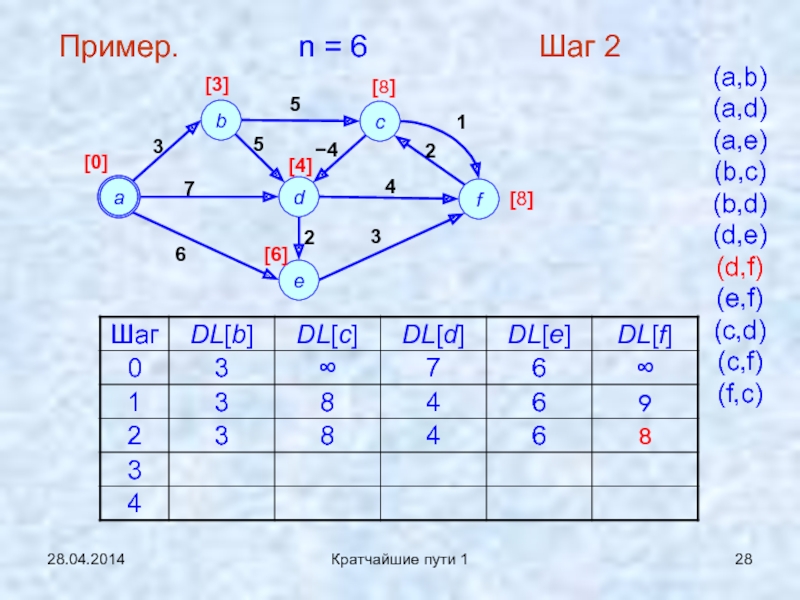
Слайд 2828.04.2014
Кратчайшие пути 1
Пример. n = 6
Шаг 2
(a,b)
(a,d)
(a,e)
(b,c)
(b,d)
(d,e)
(d,f)
(e,f)
(c,d)
(c,f)
(f,c)
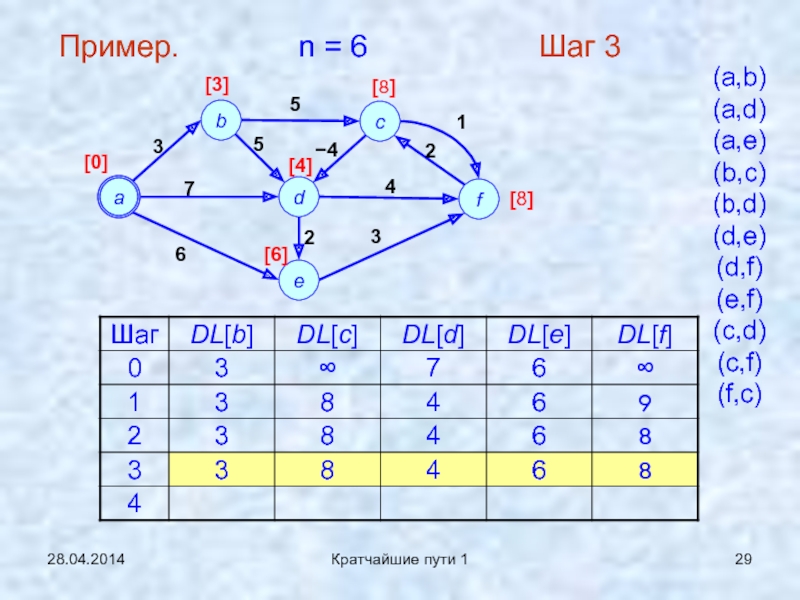
Слайд 2928.04.2014
Кратчайшие пути 1
Пример. n = 6
Шаг 3
(a,b)
(a,d)
(a,e)
(b,c)
(b,d)
(d,e)
(d,f)
(e,f)
(c,d)
(c,f)
(f,c)
Слайд 3028.04.2014
Кратчайшие пути 1
Индуктивное утверждение (“инвариант”) цикла
for (k=1; k
2); k++) {…} :
P( [1..k) ) ≡ ( d(s,v) ≤
DL[v] ≤ d[ k | v ] ) - инвариант точки входа тела цикла,P( [1..k] ) ≡ ( d(s,v) ≤ DL[v] ≤ d[k+1| v ] ) - инвариант точки выхода тела цикла,
где d[ k | v ] – длина кратчайшего из путей из s в v, содержащих не более k дуг.
Рекуррентное соотношение:
d[k+1| v ] = min {d[ k | u ] + W[u,v] ⎢ u ∈ V }
Алгоритм Форда-Беллмана
s
u
v
Сами величины d[k|v] в алгоритме не используются!
Они нужны только для записи утверждений.
Типичное соотношение динамического программирования
Слайд 3128.04.2014
Кратчайшие пути 1
Если P( [1..k) ) и P( [1..k]
) действительно инварианты, то для остановки необходимо, чтобы после k
итераций было бы k + 1 = n − 1 (т.к. путь без циклов в графе с n вершинами может иметь не более n − 1 дуг ).Отсюда k = n − 2
Покажем, что действительно тело внешнего цикла переводит P( [1..k) ) в P( [1..k] )
Корректность алгоритма Форда-Беллмана
Слайд 3228.04.2014
Кратчайшие пути 1
После очередной итерации
d(s,v) ≤ DL[v] ≤ { по
алгоритму, с учетом того, что пометки DL[u] могли уже уменьшиться
на предыдущих шагах циклов внутри одной итерации по k }≤ min {DL[u] + W[u,v] ⎢ u ∈ V } ≤
≤ min {d[ k | u ] + W[u,v] ⎢ u ∈ V } = d[ k + 1 | u ]
Корректность алгоритма Форда-Беллмана
по предположению индукции
новая
старая



![Кратчайшие пути в графе 28.04.2014Кратчайшие пути 1Пример2 – вес ребра w(i, j) [1] – расстояние d(u,v)[8] = 4 + [4] 28.04.2014Кратчайшие пути 1Пример2 – вес ребра w(i, j) [1] – расстояние d(u,v)[8] = 4 + [4]](/img/thumbs/f02d6115616dd39bdfe68c8496b7ff1c-800x.jpg)
![Кратчайшие пути в графе 28.04.2014Кратчайшие пути 1Пример[4] = − 4 + [8][8] = 5 + [3][3] = 3 + [0] 28.04.2014Кратчайшие пути 1Пример[4] = − 4 + [8][8] = 5 + [3][3] = 3 + [0]](/img/thumbs/758b30df7cfa942f7d8bf754d0673090-800x.jpg)

![Кратчайшие пути в графе 28.04.2014Кратчайшие пути 1Алгоритм нахождения кратчайшего пути продолжениеДетализация строкиu = вершина, для 28.04.2014Кратчайшие пути 1Алгоритм нахождения кратчайшего пути продолжениеДетализация строкиu = вершина, для которой DL[v]=DL[u]+W[u,v];Встать в начало Adj_In[v];do](/img/thumbs/53006e67e6a517fdba518533b39014a9-800x.jpg)

![Кратчайшие пути в графе 28.04.2014Кратчайшие пути 1Задачи вычисления расстояний от фиксированной вершиныОбщая схема большинства алгоритмов: 28.04.2014Кратчайшие пути 1Задачи вычисления расстояний от фиксированной вершиныОбщая схема большинства алгоритмов: рассматриваются временные пометки вершин dl [v],](/img/thumbs/e9e87b55d12f6c92a7ae7c412bed51e1-800x.jpg)
![Кратчайшие пути в графе 28.04.2014Кратчайшие пути 1Релаксация (ослабление) ребра u → v1dl [u]dl [v]w [u,v]dl 28.04.2014Кратчайшие пути 1Релаксация (ослабление) ребра u → v1dl [u]dl [v]w [u,v]dl [u]dl [v]w [u,v]Relax (u, v);for (∀u](/img/thumbs/1235547ef8f68e1bc62944a5d480ec81-800x.jpg)
![Кратчайшие пути в графе 28.04.2014Кратчайшие пути 1Релаксация входящих ребер относительно вершины v :for (∀u ∈ 28.04.2014Кратчайшие пути 1Релаксация входящих ребер относительно вершины v :for (∀u ∈ Adj_In[v]) Relax(u, v);В результате dl [v]](/img/thumbs/4211cb70a6912852c1454f886d2d4bca-800x.jpg)


![Кратчайшие пути в графе 28.04.2014Кратчайшие пути 1Алгоритм ДейкстрыW [ *, * ] ≥ 0Идея алгоритма: 28.04.2014Кратчайшие пути 1Алгоритм ДейкстрыW [ *, * ] ≥ 0Идея алгоритма: V = S + T,](/img/thumbs/71f1f5d5243162050158cf2fd65324c5-800x.jpg)
![Кратчайшие пути в графе 28.04.2014Кратчайшие пути 1for (∀ v ∈V) DL[v] =W[s,v];DL[s] =0; T = 28.04.2014Кратчайшие пути 1for (∀ v ∈V) DL[v] =W[s,v];DL[s] =0; T = V \ {s}; // S](/img/thumbs/af6936aac7a2d93d474608642832ca2e-800x.jpg)

![Кратчайшие пути в графе 28.04.2014Кратчайшие пути 1Корректность алгоритма: см. инвариант цикла while; от противногоАлгоритм ДейкстрыTsuu′Пусть 28.04.2014Кратчайшие пути 1Корректность алгоритма: см. инвариант цикла while; от противногоАлгоритм ДейкстрыTsuu′Пусть u = arg min { DL[p]](/img/thumbs/948c8b310d723dfe8cb44524422a8898-800x.jpg)
![Кратчайшие пути в графе 28.04.2014Кратчайшие пути 11) Множество T представляется пирамидой Heap(T) с приоритетами 28.04.2014Кратчайшие пути 11) Множество T представляется пирамидой Heap(T) с приоритетами DL[v]; при этом Inv Heap(T):](/img/thumbs/ff1334c0f8ba17bf2514b175719d62c0-800x.jpg)


![Кратчайшие пути в графе 028.04.2014Кратчайшие пути 1Алгоритм Форда-БеллманаПример непригодности алгоритма Дейкстры при произвольных весахb21Но Relax 028.04.2014Кратчайшие пути 1Алгоритм Форда-БеллманаПример непригодности алгоритма Дейкстры при произвольных весахb21Но Relax (b, c) дает DL[c] = 0](/img/thumbs/e6d105fbaf2c70b79c26cc3441be5720-800x.jpg)
![Кратчайшие пути в графе 28.04.2014Кратчайшие пути 1for (∀ v ∈ V) DL[v] =W[s,v]; DL[s] = 0; for (k=1; k 28.04.2014Кратчайшие пути 1for (∀ v ∈ V) DL[v] =W[s,v]; DL[s] = 0; for (k=1; k](/img/thumbs/15ccfd3237632190e2bcf738dc33a0a6-800x.jpg)
![Кратчайшие пути в графе 28.04.2014Кратчайшие пути 1Вариант сложности O (nm)for (∀ v ∈ V) DL[v]=W[s,v]; DL[s] =0;for (k=1; k 28.04.2014Кратчайшие пути 1Вариант сложности O (nm)for (∀ v ∈ V) DL[v]=W[s,v]; DL[s] =0;for (k=1; k](/img/thumbs/779b49b0ea6ecc05ae95fb06b9cf15b8-800x.jpg)


![Кратчайшие пути в графе 28.04.2014Кратчайшие пути 1 Если P( [1..k) ) и P( [1..k] ) 28.04.2014Кратчайшие пути 1 Если P( [1..k) ) и P( [1..k] ) действительно инварианты, то для остановки необходимо,](/img/thumbs/4faeea7abcf7baf9350f0ddf097b01a3-800x.jpg)
![Кратчайшие пути в графе 28.04.2014Кратчайшие пути 1После очередной итерацииd(s,v) ≤ DL[v] ≤ { по алгоритму, 28.04.2014Кратчайшие пути 1После очередной итерацииd(s,v) ≤ DL[v] ≤ { по алгоритму, с учетом того, что пометки DL[u]](/img/thumbs/aeed28c2bd9540591782a26cb3a1e051-800x.jpg)