Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
КРАЙГИНГ-интерполяция Даниель Криге (статистическая интерполяция)
Содержание
- 1. КРАЙГИНГ-интерполяция Даниель Криге (статистическая интерполяция)
- 2. Основные определенияКрайгинг-интерполяция основана на понятии регионализированной переменной.Регионализованная
- 3. Пространственные данныеНа практике, как правило, даже реализация
- 4. Гипотеза универсального крайгингаЕсли СФ допускает представление
- 5. Ключевым понятием метода является
- 6. Чем интересен этот вид интерполяции в задачах
- 7. Среднее случайной функцииСреднее случайной функции или математическое
- 8. Вариограмма – структурная функцияДля описания статистической структуры
- 9. Вариограммное облакоВариограммное облако это график всех пар
- 10. Экспериментальная вариограммаДискретная функция, описывающая поведение среднего значения
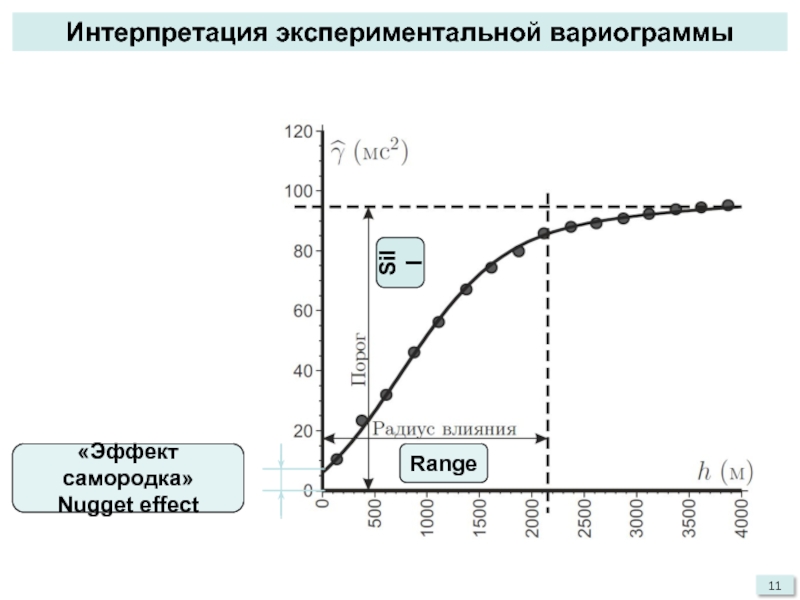
- 11. Интерпретация экспериментальной вариограммыSillRange«Эффект самородка»Nugget effect
- 12. Поведение в окрестности нуляа) параболическое поведение –
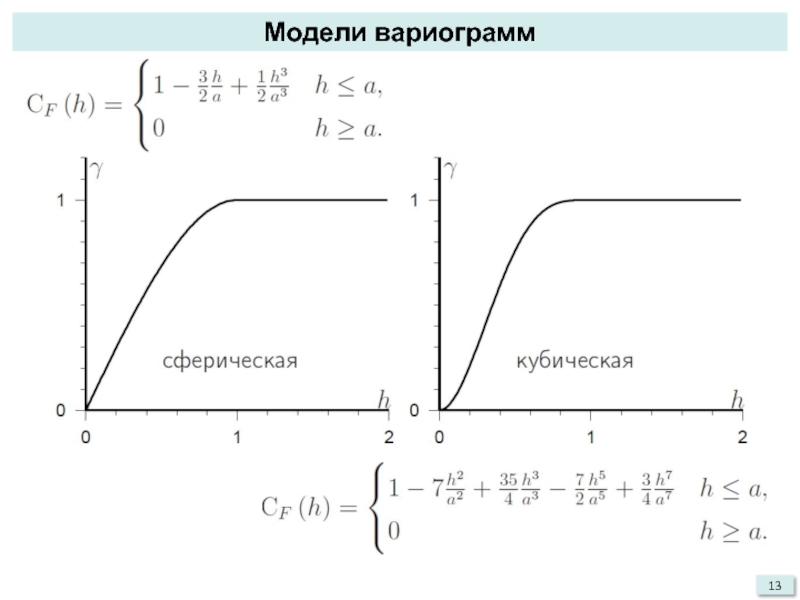
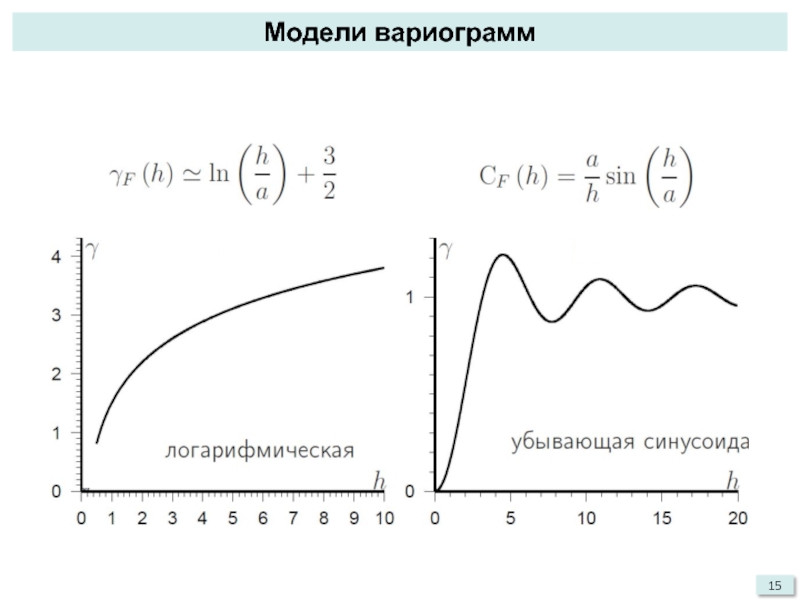
- 13. Модели вариограмм
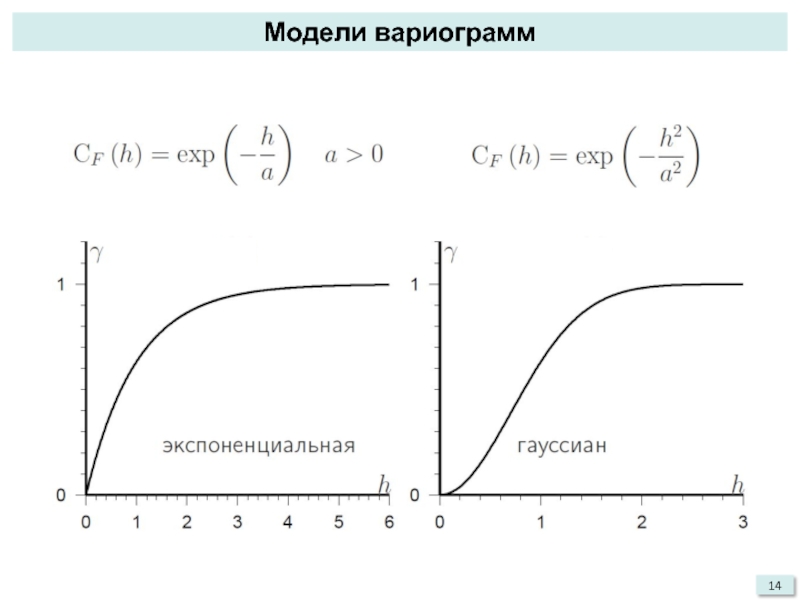
- 14. Модели вариограмм
- 15. Модели вариограмм
- 16. Скачать презентанцию
Основные определенияКрайгинг-интерполяция основана на понятии регионализированной переменной.Регионализованная переменная – функция зависящая от координат пространства f (r), характеризующаяся двумя особенностями:локальная случайная особенность, которая может быть описана случайной переменной,пространственная зависимость, описываемая корреляционными соотношениями
Слайды и текст этой презентации
Слайд 1КРАЙГИНГ-интерполяция
Даниель Криге
(статистическая интерполяция)
Функция определена на ограниченном множестве точек.
Необходимо получить оценку
фунции в любой точке плоскости.
задача не имеет единственного решения.Слайд 2Основные определения
Крайгинг-интерполяция основана на понятии регионализированной переменной.
Регионализованная переменная – функция
зависящая от координат пространства f (r), характеризующаяся двумя особенностями:
локальная случайная
особенность, которая может быть описана случайной переменной,пространственная зависимость, описываемая корреляционными соотношениями между парами случайных переменных.
Геостатистика – методология изучения регионализованных переменных с помощью вероятностных методов.
Слайд 3Пространственные данные
На практике, как правило, даже реализация случайной функции не
известна во всей области D, она описывается набором значений
е известным в определённом конечном счётном множестве точек. Этот набор называется пространственными данными или регионализованными данными.Слайд 4Гипотеза универсального крайгинга
Если СФ допускает представление
- среднее СФ которое может быть представлено в виде
- некоторые известные функции, - коэффициенты- стационарная в широком смысле с нулевым средним СФ
Слайд 5 Ключевым понятием метода является модельная полувариограмма (l), описывающая функцию полу-расхождения
интерполируемых значений в зависимости от расстояния l между ними. Весовые
множители определяются из условия минимума погрешности прогноза, вычисляемой по формуле:Слайд 6Чем интересен этот вид интерполяции в задачах интерпретации сейсмических данных?
Не
создает краевых эффектов
Допускает учесть погрешность наблюдений
Допускает оценить погрешность интерполяции
Слайд 7Среднее случайной функции
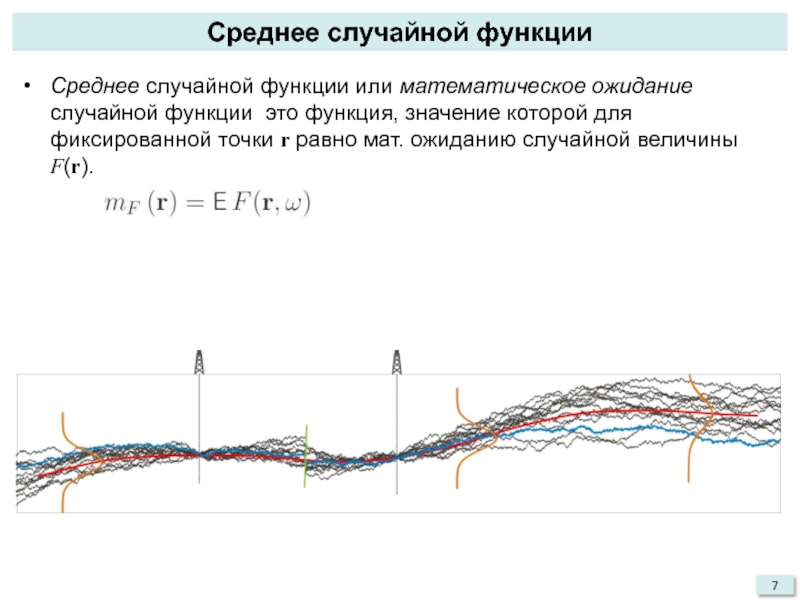
Среднее случайной функции или математическое ожидание случайной функции
это функция, значение которой для фиксированной точки r равно мат.
ожиданию случайной величины F(r).Слайд 8Вариограмма – структурная функция
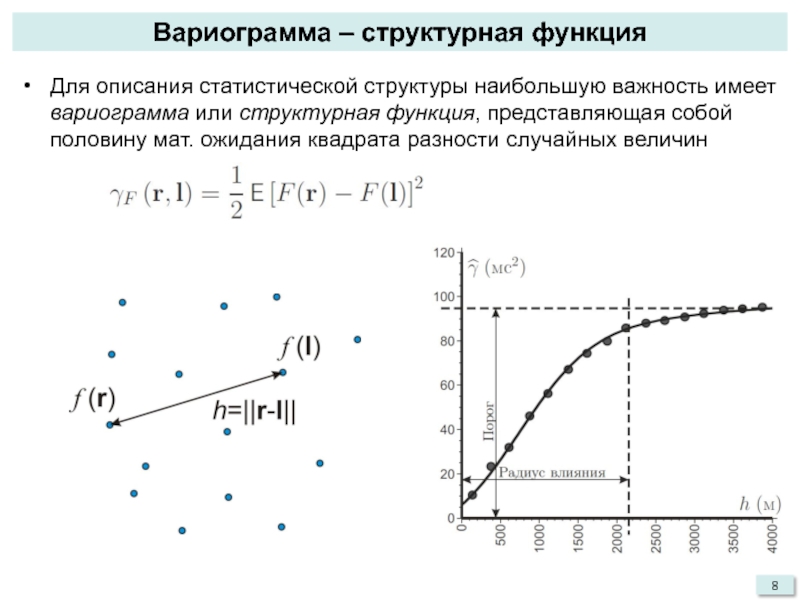
Для описания статистической структуры наибольшую важность имеет
вариограмма или структурная функция, представляющая собой половину мат. ожидания квадрата
разности случайных величинСлайд 9Вариограммное облако
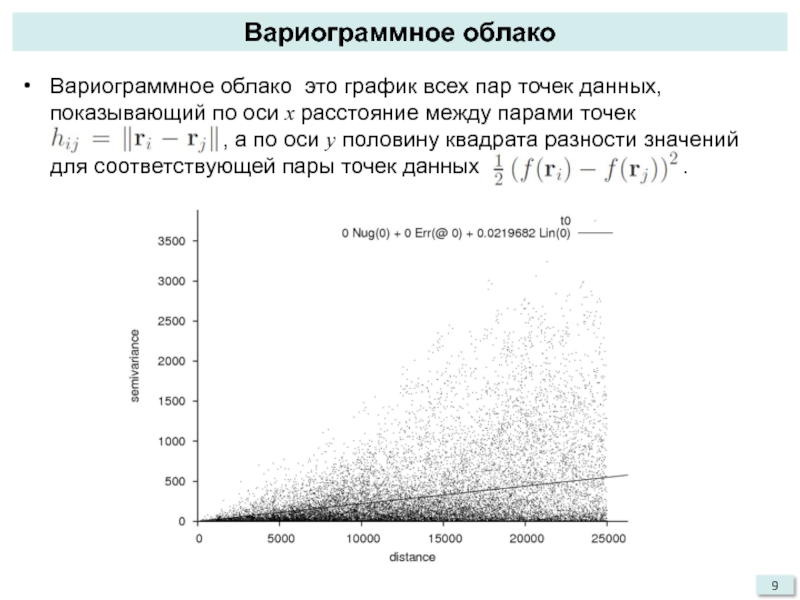
Вариограммное облако это график всех пар точек данных, показывающий
по оси x расстояние между парами точек
a , а по оси y половину квадрата разности значений для соответствующей пары точек данных .Слайд 10Экспериментальная вариограмма
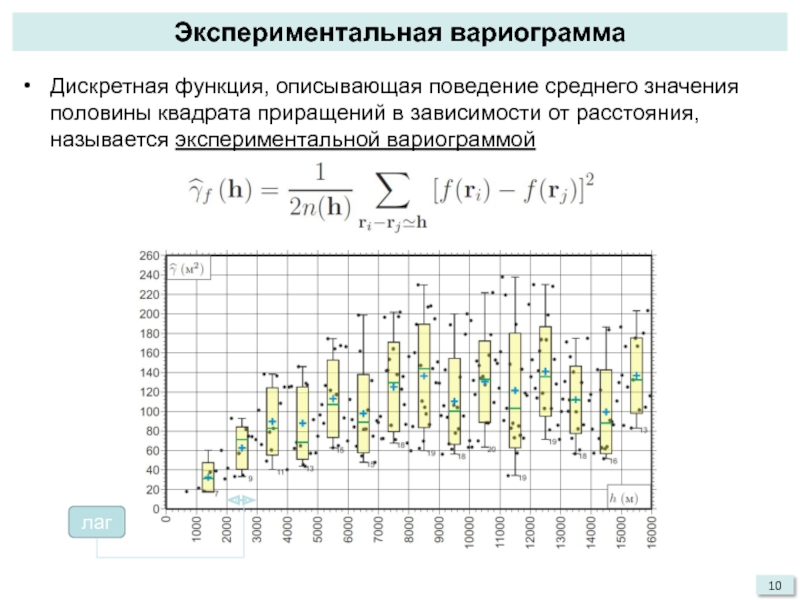
Дискретная функция, описывающая поведение среднего значения половины квадрата приращений
в зависимости от расстояния, называется экспериментальной вариограммой
лаг
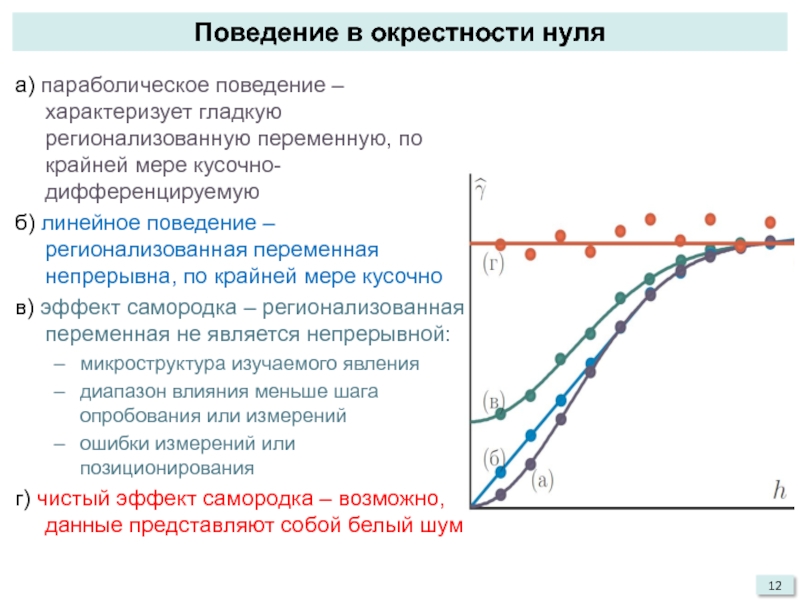
Слайд 12Поведение в окрестности нуля
а) параболическое поведение – характеризует гладкую регионализованную
переменную, по крайней мере кусочно-дифференцируемую
б) линейное поведение –регионализованная переменная непрерывна,
по крайней мере кусочнов) эффект самородка – регионализованная переменная не является непрерывной:
микроструктура изучаемого явления
диапазон влияния меньше шага опробования или измерений
ошибки измерений или позиционирования
г) чистый эффект самородка – возможно, данные представляют собой белый шум