Криптографические методы и средства для защиты информации 2

другой – секретный.
1)Если открытый ключ используется для шифрования, а

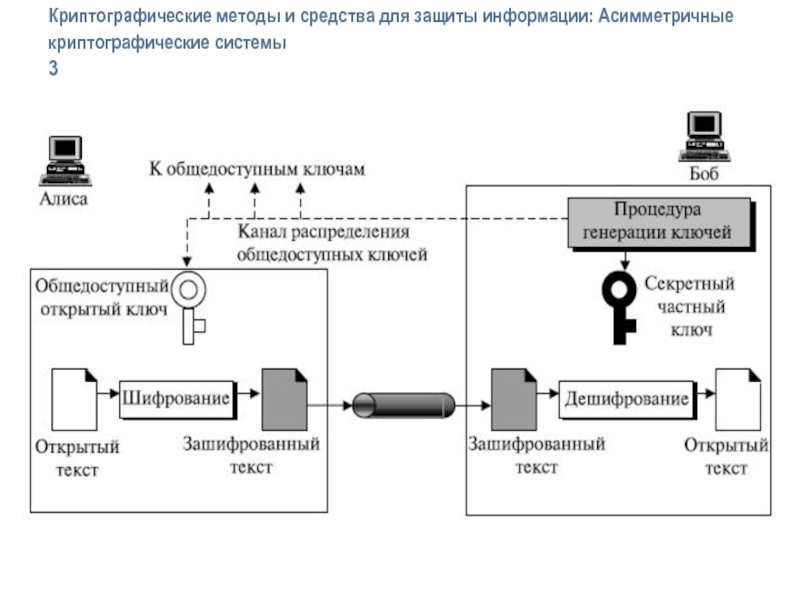
секретный ключ – для расшифрования, то такие криптосистемы называются криптосистемами с открытым ключом.
C = Eko( P ), P = Dkc( C ) = Dkc(Eko( P ))
2)Если секретный ключ используется для шифрования, а открытый ключ – для расшифрования, то имеет место система электронной подписи (ЭП). Владелец секретного ключа может зашифровать (подписать) текст, а проверить правильность подписи (расшифровать) может любой пользователь, имеющий в своем распоряжении открытый ключ.
C = Ekc( P ), P = Dko( C ) = Dko(Ekc( P ))

Криптографические методы и средства для защиты информации: Асимметричные криптографические системы 1

преобразования и два различных, но взаимосвязанных друг с другом ключа:

открытый, доступный каждому для шифрования, другой - секретный ключ доступен только одному лицу для расшифрования.
Методы шифрования должны обладать двумя свойствами:
законный получатель сможет выполнить обратное преобразование и расшифровать сообщение
злоумышленник или криптоаналитик противника, перехвативший сообщение, не сможет восстановить по нему открытый текст без таких затрат времени и средств, которые сделают эту работу нецелесообразной.

Криптографические методы и средства для защиты информации: Асимметричные криптографические системы 2

3

Меркле-Хеллмана)

Дискретное возведение в степень (метод Эль-Гамаля)
 
Криптографические методы и средства для

защиты информации: Асимметричные криптографические системы 4

правило, по которому связывают (отображают) один элемент во множестве A, называемый

доменом, и один элемент во множестве B, называемый диапазоном.
Обратимая функция — функция, которая связывает каждый элемент в диапазоне с точно одним элементом в домене.
Односторонняя функция (OWF — One Way Function) — функция, которая обладает следующими двумя свойствами:
f вычисляется просто. Другими словами, при данном x может быть легко вычислен  y = f (x).
f -1 вычисляется трудно.
Другими словами, при данном y, вычисление 
x= f ~1 (y) неосуществимо.

Криптографические методы и средства для защиты информации: Асимметричные криптографические системы 5

т.к. законный получатель не сможет расшифровать.
Она должна иметь «потайную лазейку»,

т.е. должен существовать эффективный способ ее вычисления в обоих направлениях. При этом знание прямого преобразования не позволит легко найти обратное преобразование.
"Лазейка" в односторонней функции
"Лазейка" в односторонней функции (TOWF — Trapdoor One Way) — односторонняя функция с третьим свойством:
При данном  y и ловушке (секретной) x может быть легко вычислен.
Вычисление ключей осуществляется получателем сообщения, который оставляет у себя ключ для расшифрования - секретный, открытый ключ он высылает отправителю сообщений любым доступным способом или публикует, не опасаясь огласки.
Особенность этих методов заключается в том, что функции шифрования и расшифрования являются обратимыми только тогда, когда они обеспечиваются строго определенной парой ключей. При этом открытый ключ определяет конкретную реализацию функции «ловушки», а секретный ключ дает информацию о «ловушке».

Криптографические методы и средства для защиты информации: Асимметричные криптографические системы 6

– прямое преобразование.
Эффективного алгоритма для обратной операции – извлечения корня

m-ой степени по модулю n для произвольных m и n не найдено. Это проблема дискретного логарифмирования для больших чисел.
Один из методов использует алгоритм извлечения корня при известном разложении числа n на простые множители, это и позволяет отнести функцию F(x) к классу односторонних функций с «потайной лазейкой».
Число Y является открытым ключом Число Y открыто передается или публикуется.
Число m является секретным ключом.

Криптографические методы и средства для защиты информации: Асимметричные криптографические системы 7

криптоалгоритм Меркле-Хеллмана.
Пусть задан набор целых положительных чисел А=(а1,а2…аn) и известна

некоторая величина Z. Задачей является нахождение таких чисел аi , если это возможно, сумма которых равна числу Z.
В простейшем случае это число Z указывает размер рюкзака , а каждое из чисел аi – размер предмета, который нужно уложить в рюкзак. Задачей является нахождение такого набора предметов, чтобы рюкзак был полностью заполнен.
Пример: Z=3231 и набор из 10 чисел
А=(43, 129, 215, 473, 903,302, 561, 1165,697, 1523)
Заметим, что число Z получится при сложении только некоторых чисел аi.
В принципе решение может быть найдено полным перебором подмножеств А и проверкой , какая из ∑ аi равна числу Z. В нашем примере этот перебор состоит из 210 комбинаций, включая пустое множество.
Решение Z= 3231= 129 + 473 +909 + 561 + 1165.

Криптографические методы и средства для защиты информации: Асимметричные криптографические системы 8

операциях с большими (скажем, 100-значными) простыми числами и их произведениями.

В 1976 году преподаватели Стэнфордского университета, Витфильд Диффи (Whitfield DifFie) и Мартин Хелман (Martin Heliman), предложили систему под названием "шифрование с применением открытого ключа". Этот метод предполагает наличие двух ключей при каждом сеансе кодирования и хорошо отрекомендовал себя даже в незащищенных сетях. Каждый пользователь создает два ключа. Каждый ключ представляет собой произвольный набор цифр объемом в некоторых случаях более чем в 500 цифр. Оба ключа связаны между собой таким образом, что сообщение можно зашифровать с помощью одного ключа и расшифровать с помощью другого, однако расшифровать сообщение с помощью ключа, использовавшегося для его зашифровки, нельзя.

Криптографические методы и средства для защиты информации: Асимметричные криптографические системы 9

разработали алгоритм для реализации метода криптографии на основе открытого ключа.

Криптосистема получила название RSA, по первым буквам фамилий ее авторов — Рона Ривеста (Ron Rivest), Эйди Шамира (Adi Shamir) и Леонарда Эдлемана (Leonard Adleman) (http://www.rsa.org/).

Криптографические методы и средства для защиты информации: Асимметричные криптографические системы 10

«Юлий Цезарь» В. Шекспира «ITS ALL GREEK TO ME», она

сначала была записана в виде целого числа Х стандартным способом (A=01, B=02,…..Z=26,пробел =00), затем зашифрована
Xe mod m, где m – 129-разрядное целое число, e=9007.
Шифротекст и числа e и m были опубликованы.
Конечно, многие математики пытались найти способ раскрыть алгоритм криптосистемы с открытым ключом с помощью вычислений (часто весьма объемных), однако пока что никому не удалось найти решение этой математической проблемы. Декодирующие программы используют метод "грубой силы", проверяя все возможные комбинации. Теоретически такой подход позволяет добиться успеха, однако необходимый объем вычислений делает такой вариант нереальным при условии, конечно, что открытый ключ имеет достаточную длину.
Лишь в 1994 году через 17 лет фраза была расшифрована, для этого потребовалось 220 дней, были задействованы 600 человек и 1600 компьютеров, соединенных через Интернет.

Криптографические методы и средства для защиты информации: Асимметричные криптографические системы 11

P и Q и вычисляет два произведения N =

PxQ , M = (P – 1)x(Q – 1)
Затем выбирается случайное число E, взаимно простое с M и вычисляется D, удовлетворяющее условию (E x D = 1) mod M
Получатель публикует E и N, как свой открытый ключ, сохраняя D, как секретный ключ.
Отправитель сообщение X представляет в виде набора блоков
xi = (x1, x2, ……xl), 0 < xi < M, затем шифрует его с использованием E и N.
Каждое xi возвести в степень E по модулю N, получится шифрованное сообщение:
(x1 E mod N), (x2 E mod N),……. (x1 E mod N)
Для расшифрования полученного сообщения Получатель, используя свой секретный ключ D, вычисляет для каждого блока
(xi ED mod N), т.к. (ExD = 1) mod M, то утверждается xi ED mod N = xi

Криптографические методы и средства для защиты информации: Асимметричные криптографические системы 12

. Пример:

13

в системе с открытым ключом;
как средство аутентификации пользователей в системах

ЭЦП;
как средство для распределения ключей в составных системах.

Криптографические методы и средства для защиты информации: Асимметричные криптографические системы 14