Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Критерии подобия. π-теорема и ее следствия. Определение критериев подобия с
Содержание
- 1. Критерии подобия. π-теорема и ее следствия. Определение критериев подобия с
- 2. Основы научных исследований1. Критерии подобия Критерии подобия
- 3. Основы научных исследованийНапример, критериями практического подобия двух
- 4. Основы научных исследованийПри создании крупных машин первоначально
- 5. Основы научных исследованийЛопастная машина состоит из подвода,
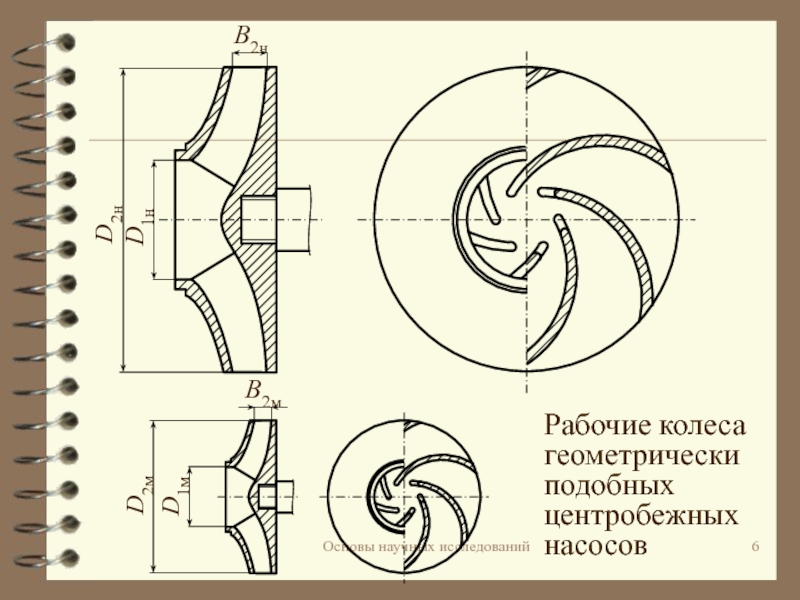
- 6. Основы научных исследованийРабочие колеса геометрически подобных центробежных насосов
- 7. Основы научных исследований2. π-теорема и ее следствияВ
- 8. Основы научных исследованийИз теоремы следует два важных
- 9. Основы научных исследованийПредположим, что процессы в объекте
- 10. Основы научных исследованийСложен также анализ результатов эксперимента,
- 11. Основы научных исследованийДля получения данных, одинаково достоверных
- 12. Основы научных исследований3. Определение критериев подобия с
- 13. Основы научных исследованийНа втором этапе выбирается система
- 14. Основы научных исследованийИспользуя размерности основных единиц, можно
- 15. Основы научных исследованийНа третьем этапе определяются критерии
- 16. Основы научных исследованийПример. Определение критериев подобия процесса
- 17. Основы научных исследованийШар помещен в трубопровод настолько
- 18. Основы научных исследованийФормулы размерностей фундаментальных переменныхСила взаимодействия шара и потока жидкостиСкорость жидкостиПлотность жидкостиДинамическая вязкость жидкостиДиаметр шараFM L T-2vL T-1ρM L-3μM L-1 T-1dL
- 19. Основы научных исследованийКритерий (безразмерная комбинация) в общем
- 20. Основы научных исследованийЕсли зависимость справедлива относительно пере-менных,
- 21. Основы научных исследованийВыразим переменные b, c и
- 22. Основы научных исследованийТак как μ / ρ = γ — кинематический
- 23. Скачать презентанцию
Слайды и текст этой презентации
Слайд 1Критерии подобия. π-теорема и ее следствия. Определение критериев подобия с
использованием теории размерностей.
Слайд 2Основы научных исследований
1. Критерии подобия
Критерии подобия — безразмерные комбинации,
которые составлены из физических величин, описывающих процессы в исследуемых объектах
Критерии
подобия должны обладать четким физическим смысломОбозначаются критерии буквой π
В соответствии с теорией подобия при эксперимен-тах необходимо измерять все величины, входящие в состав критериев
Обрабатывать результаты следует в виде зависимо-стей между критериями подобия. Полученные таким образом зависимости будут справедливы не только для данного эксперимента, но и для всех подобных объектов
Слайд 3Основы научных исследований
Например, критериями практического подобия двух однотипных лопастных машин,
работающих в установившихся режимах, являются безразмерный напор π1 и безразмерная
подача π2Зависимость безразмерного напора от безразмерной подачи представляет собой безразмерную (типовую) напорную характеристику лопастной машины
Она не связана с размерами, частотой вращения ротора и плотностью жидкости, а характеризует только особенности гидродинамической схемы и является одинаковой для всего семейства лопастных машин
H — напор насоса
Q — подача насоса
n — частота вращения ротора
D2 — диаметр рабочего колеса
Слайд 4Основы научных исследований
При создании крупных машин первоначально изготовляет несколько небольших
моделей различных гидродинамических схем и проводят их испытания
Пропорциональность сходственных параметров,
входящих в условия однозначности, для лопастных машин, работающих в установившихся режимах, выполняется при их геометрическом подобии, которое требует одинаковости форм и одинакового отношения сходственных размеров. Определяя критерии π1 и π2 для различных режимов, строят график зависимости π1 от π2 — безразмерную характеристику, а затем по законам подобия опре-деляют размеры, частоту вращения и строят зависи-мость напора от подачи для натурной машины
Геометрическое подобие является обязательным условием практического подобия большинства объектов
Слайд 5Основы научных исследований
Лопастная машина состоит из подвода, рабочего колеса и
отвода. Два рабочих колеса, например, радиальной машины, будут геометрически подобными,
если число и форма лопаток у них будут одинаковыми, а сходственные размеры будут находиться в соотношениигде D1н, D2н, B2н и D1м, D2м, B2м — диаметр входа, диаметр и ширина колеса соответственно натурной и модельной машин
Для геометрического подобия лопастных машин, кроме рабочих колес, должно быть соблюдено подобие их подводов и отводов
Слайд 7Основы научных исследований
2. π-теорема и ее следствия
В соответствии с π-теоремой,
если процесс в объекте характеризуется m фундаментальными физическими величинами, для
выражения размерностей которых используется k основных единиц, то этот процесс можно описать m – k безразмерными комбинациями, составленными из этих величинСлайд 8Основы научных исследований
Из теоремы следует два важных вывода:
1. Уравнения, описывающие физические
процессы, могут быть выражены уравнениями связи между безразмерными комбинациями —
критериями подобия. Последние уравнения будут справедливы для всех подобных объектов2. Число независимых критериев равно m – k, т.е. меньше числа размерных физических переменных на число основных единиц. Уменьшение числа переменных, которыми описывают процесс, ведет к уменьшению объема экспериментальных исследований и делает результаты более наглядными
Слайд 9Основы научных исследований
Предположим, что процессы в объекте описывают-ся m = 5 фундаментальными
физическими величи-нами. Одна из них выходная — параметр и четыре
входных — факторыРешено экспериментальным путем установить связь между выходной и входными величинами, не прибегая к безразмерным комбинациям
Пусть при постановке опытов каждый фактор будет фиксироваться на пяти уровнях. В этих условиях для перебора всех возможных сочетаний необходи-мое число опытов, равное сложности объекта, составит C = 54 = 625. Выполнить такое количество опытов весьма затруднительно
Слайд 10Основы научных исследований
Сложен также анализ результатов эксперимента, поскольку необходимо получить
зависимость в виде функции четырех переменных. Подобрать такую зависимость весьма
сложно. Кроме того, результаты опытов практически невозможно будет представить графическиПерейдем к безразмерным комбинациям. Предположим, что число основных единиц k = 3 — это очень часто встречающийся случай при иссле-довании механических и гидравлических систем
В условиях рассматриваемого примера в соответ-ствии с π-теоремой после перехода к критериям подобия число безразмерных переменных составит m – k = 5 – 3 = 2. Одна из них — безразмерный параметр, вторая — обобщенный безразмерный фактор
Слайд 11Основы научных исследований
Для получения данных, одинаково достоверных с данными экспериментов
без использования критериев подобия, в последнем случае достаточно будет поставить
не 625, а всего 5 опытов.При переходе к безразмерным комбинациям упрощается анализ и графическое представление информации. Зависимость безразмерного параметра от обобщенного безразмерного фактора описыва-ется функцией одной переменной и будет представ-лена на графике одной линией
Известны два способа определения критериев подобия: с помощью анализа размерностей и по уравнениям процесса
Слайд 12Основы научных исследований
3. Определение критериев подобия с использованием теории размерностей
Решение
этой задачи состоит из трех этапов:
На первом этапе выбираются фундаментальные
переменные — параметры и факторы.Для правильного выбора факторов (входных переменных) необходимо глубокое проникновение в суть исследуемого объекта. Часто это требует не только изучения априорной информации, но и постановки предварительных экспериментов. Если после выбора фундаментальных переменных система безразмерных комбинаций не получается, то необходимо возвратиться к анализу объекта исследования.
Слайд 13Основы научных исследований
На втором этапе выбирается система основных единиц для
выражения размерностей фундамен-тальных переменных
В качестве основных рекомендуется принимать основные единицы
СИ:длины
l
L
метр
массы
m
M
килограмм
времени
t
T
секунда
силы тока
I
I
ампер
температуры
θ
K
кельвин
количества
вещества
n
N
моль
силы света
J
J
кандела
Слайд 14Основы научных исследований
Используя размерности основных единиц, можно составить формулы размерностей
всех фундаментальных переменных.
Например, известно, что сила определяется зависимостью
F = ma
Формула размерности силы
определяется как произ-ведение формул размерности массы и ускоренияЗаписав формулы размерностей всех фундаменталь-ных переменных, описывающих процессы в объекте, устанавливают, какие размерности основных единиц в них входят. Эти единицы и будут составлять систему основных единиц в условиях конкретной задачи
Слайд 15Основы научных исследований
На третьем этапе определяются критерии подобия с использованием
теории размерностей.
Для размерной функциональ-ной зависимости
размерности левой и правой частей
должны быть равны:или
Слайд 16Основы научных исследований
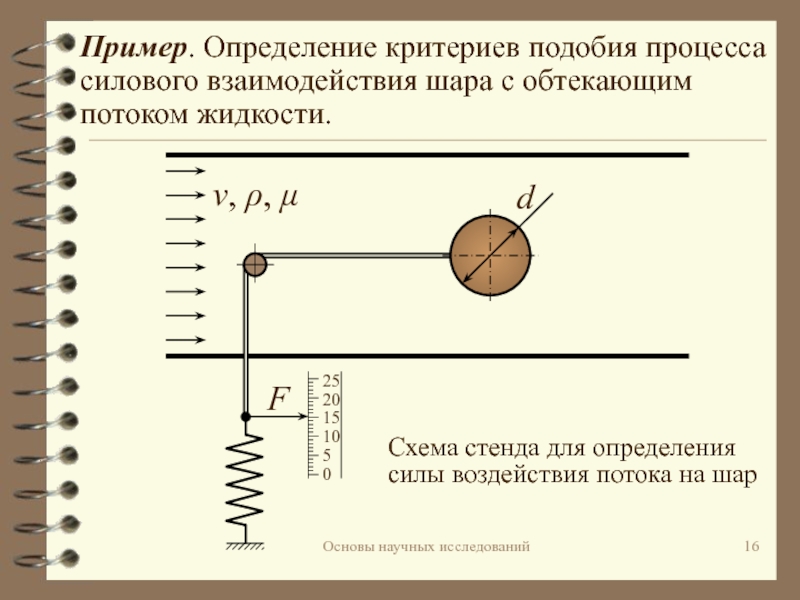
Пример. Определение критериев подобия процесса силового взаимодействия шара
с обтекающим потоком жидкости.
Схема стенда для определения силы воздействия потока
на шарv, ρ, μ
F
Слайд 17Основы научных исследований
Шар помещен в трубопровод настолько большого внутреннего диаметра,
что стеснением им потока можно пренебречь. Гибкой нитью шар связан
через блок с пружинным динамометром.Усилие F зависит от свойств шара и потока.
Если шероховатостью шара можно пренебречь, его свойства определяются одной переменной — диаметром d.
Свойства потока оцениваются средней скоростью v, плотностью ρ и вязкостью μ жидкости. Таким образом, в рассматриваемое случае фундаментальных переменных пять: параметр F и факторы d, v, ρ и μ.
Слайд 18Основы научных исследований
Формулы размерностей фундаментальных переменных
Сила взаимодействия шара и потока
жидкости
Скорость жидкости
Плотность жидкости
Динамическая вязкость жидкости
Диаметр шара
F
M L T-2
v
L T-1
ρ
M L-3
μ
M L-1 T-1
d
L
Слайд 19Основы научных исследований
Критерий (безразмерная комбинация) в общем случае может быть
представлен произведением фундаментальных переменных в определенных степенях.
где x, y,
z, u, w — показатели степенейВ рассматриваемом случае
Показатели могут быть целыми, дробными, положи-тельными и отрицательными числами. Они могут принимать и нулевое значение. В последнем случае критерий не будет зависеть от соответствующей фундаментальной переменной
Представим искомую зависимость в виде
где a, b, c, e, f — неизвестные показатели степеней
Слайд 20Основы научных исследований
Если зависимость справедлива относительно пере-менных, то она будет
справедлива и относительно размерностей. Подставим в уравнение вместо пере-менных их
размерности. Левую часть уравнения представим произведением размерностей в нулевых степеняхЧтобы последнее выражение было справедливым, должны выполняться условия равенства показате-лей степени для каждой из трех основных единиц
для M
для L
для T
Слайд 21Основы научных исследований
Выразим переменные b, c и e через a
и f и подставим в искомую зависимость
Объединим члены, имеющие одинаковые
показатели степенейe = – a – f ;
c = –2a – f ;
b = –2a – f
В качестве критериев подобия
могут быть приняты комплексы:
— безразмерное усилие
Усилие, действующее со стороны потока на шар, делится на произведение площади квадрата, сторона которого равна диаметру шара (d 2) и удвоенного скоростного давления ρv2
Слайд 22Основы научных исследований
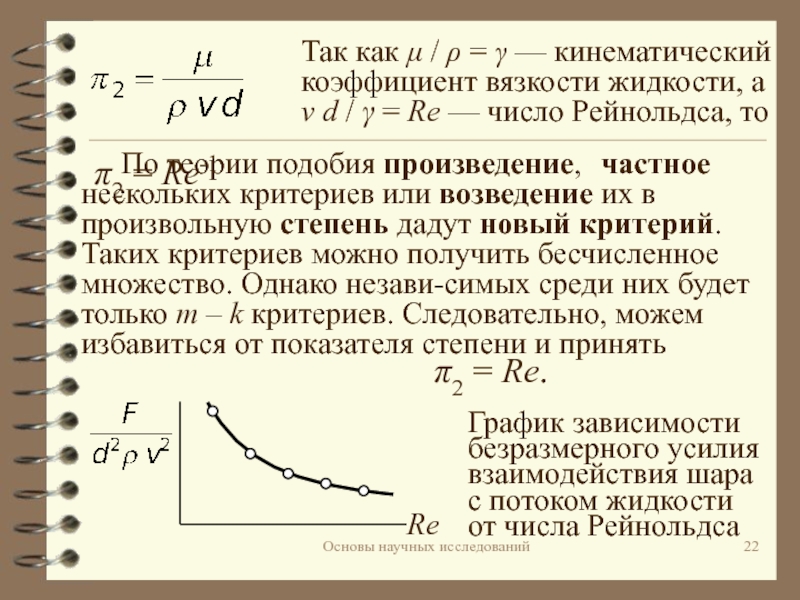
Так как μ / ρ = γ — кинематический коэффициент вязкости жидкости,
а v d / γ = Re — число Рейнольдса, то
π2 = Re-1
По теории подобия
произведение, частное нескольких критериев или возведение их в произвольную степень дадут новый критерий. Таких критериев можно получить бесчисленное множество. Однако незави-симых среди них будет только m – k критериев. Следовательно, можем избавиться от показателя степени и принять π2 = Re.
График зависимости безразмерного усилия взаимодействия шара
с потоком жидкости
от числа Рейнольдса