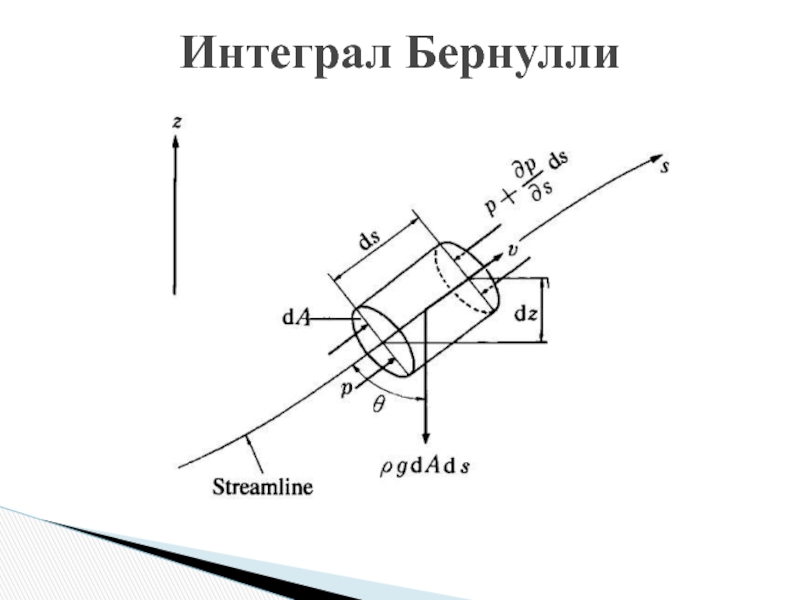
«жидкая» в том смысле, что ее вязкость несущественна. Таким образом
мы делаем приближение, которое описывает некое идеальное вещество, а не реальную жидкость.Об огромной разнице, возникающей в зависимости от того, рассматриваем ли мы вязкость или нет, в свое время хорошо знал Джон фон Нейманн. Известно ему было и то, что во времена наибольшего расцвета гидродинамики, т. е. примерно до 1900 г., основные усилия были направлены на решение красивых математических задач в рамках именно этого приближения, которое ничего не имеет общего с реальными жидкостями. Поэтому теоретиков, которые занимались подобными веществами, он называл людьми, изучающими «сухую воду». Они отбрасывали важнейшее свойство жидкости
Идеальная жидкость