Курс лекций по сопротивлению материалов

материала и геометрии объекта. Внешние силы. Метод сечений. Внутренние усилия.

Напряжения. Перемещения и деформации.
Центральное растяжение-сжатие. Принцип Сен-Венана. Напряжения и деформации. Коэффициент Пуассона. Закон Гука. Модуль упругости. Напряжения на наклонных площадках. Внутренние усилия при растяжении-сжатии.
Перемещения при растяжении сжатии. Учет собственного веса. Статически неопределимые системы при растяжении сжатии.
Испытание материалов на растяжение-сжатие. Характеристики прочности и пластичности. Идеализированные диаграммы. Потенциальная энергия деформации (полная, удельная).
Диаграмма сжатия. Основные механические характеристики. Особенности разрушения пластических и хрупких материалов при растяжении-сжатии малоуглеродистой стали и чугуна.
Основные сведения о расчете конструкций. Методы допускаемых напряжений и предельных состояний.
Основные типы опор и балок. Чистый и поперечный изгиб. Внутренние усилия при изгибе. Дифференциальные зависимости. Построение эпюр поперечных сил и изгибающих моментов.
Изгиб балок. Основные допущения. Нормальные напряжения при чистом изгибе. Момент сопротивления при изгибе. Условие прочности по нормальным напряжениям. Понятие рационального сечения при изгибе.
Вывод формулы касательных напряжений при поперечном изгибе. Распределение касательных напряжений для некоторых типов поперечных сечений. Условие прочности на сдвиг. Понятие центра изгиба.
Понятие о чистом сдвиге. Закон Гука при сдвиге. Связь между модулями упругости при растяжении и сдвиге. Кручение стержней круглого поперечного сечения. Напряжения и перемещения. Анализ напряженного состояния.

и его интегрирование.
Основы расчета статически неопределимых балок по методу

сил. Степень статической неопределимости, основная система, уравнения совместности деформаций.
Сложное сопротивление. Построение эпюр внутренних усилий в пространственном ломанном стержне.
Одновременное действие продольной силы и изгибающих моментов. Определение нормальных напряжений и положения нулевой линии. Косой изгиб.
Общие понятия о теориях прочности. Критерий разрушения путем отрыва (хрупкое разрушение). Краткие сведения от первой и второй теориях прочности. Теория прочности Мора.
Критерий пластического состояния. Третья и четвертая теории прочности. Оценка прочности с применением теорий прочности. Понятия о новых теориях прочности и механики разрушения.
Понятие об устойчивых и неустойчивых формах равновесия. Формула Эйлера. Учет влияния способов закрепления концов стержня.
Пределы применимости формулы Эйлера. Формула Ясинского. Порядок определения критической нагрузки. Практический метод расчета сжатых стержней по нормам.

Рекомендуемая литература
1 Ицкович Г.М. Сопротивление материалов: Учеб. пособие.-9-е изд., стер.-М.: Высш. шк., 2001. –368с.: ил.
2 Сопротивление материалов. Учеб. Пособие / Н.А. Костенко, С.В. Балясникова, Ю.Э. Волошановская и др.; Под. Ред. Н.А. Костенко. –М.: Высш. Шк., 2000.-430с.:ил
3 Ицкович Г.М., Минин Л.С., Винокурова А.И. Руководство к решению задач по сопротивлению материалов: Учеб. пособие для вузов/ Под ред. Л.С. Минина.-3-е изд., перераб. и доп. –М.: Высш. шк., 2001.-592 с.:ил.
4 Эрдеди А.А. Эрдеди Н.А. Теоретическая механика. Сопротивление материалов.: Учеб пособие.-4-е изд., перераб. и доп.-М.: Высш.шк.; Издательский центр "Академия",2001.-318с.

материала и геометрии объекта. Внешние силы. Метод сечений. Внутренние усилия.

Введение
Сопротивление материалов является частью более общей науки – механики твердого деформируемого тела, в которую входят: теория упругости, теории пластичности и ползучести, теория сооружений, строительная механика, механика разрушения и др. Задачей сопротивления материалов является изучение методов расчета простейших элементов конструкций и деталей машин на прочность, жесткость и устойчивость.
















Прочностью называется способность элемента конструкции сопротивляться воздействию приложенных к нему сил не разрушаясь.
Жесткостью называется способность элемента конструкции сопротивляться воздействию приложенных к нему сил, получая лишь малые упругие деформации.
Устойчивостью называется способность элемента конструкции сохранять первоначальную форму равновесия под действием приложенных сил.
Реальные тела не являются абсолютно твердыми и под действием приложенных к ним сил изменяют свою первоначальную форму и размеры, то есть деформируются. Деформации тела, исчезающие после снятия внешних сил, называются упругими, а не исчезающие – остаточными или пластическими.
Определение размеров деталей или внешних нагрузок, при которых исключается возможность разрушения деталей, является целью расчета на прочность.
Определение размеров деталей или внешних нагрузок, при которых исключается возможность появления недопустимых с точки зрения нормальной работы конструкции деформаций этих деталей, является целью расчета на жесткость.

Механика твердого деформируемого тела

Строительные конструкции

Теория пластичности и ползучести

Теория сооружений

Механика подземных сооружений

Строительная механика

Механика грунтов

Сопротивление материалов

Детали машин

Прикладная механика

Теория упругости

Механика разрушения

Реальный объект и расчетная схема
Реальный объект, освобожденный от несущественных особенностей, не влияющих заметным образом на работу системы в целом, называется расчетной схемой. Переход от реального объекта к расчетной схеме осуществляется путем схематизации свойств материала, системы приложенных сил, геометрии реального объекта, типов опорных устройств и т.д.
Схематизация свойств материала
Реальные материалы обладают разнообразными физическими свойствами и характерной для каждого из них структурой.
С целью упрощения расчетов в сопротивлении материалов используются следующие допущения о свойствах материала.
1. Материал считается однородным, если его свойства во всех точках одинаковы.
2. Материал считается изотропным, если его свойства во всех направлениях одинаковы.

Изотропными являются аморфные материалы, такие как стекло и смолы.
Анизотропными являются пластмассы, текстолит и т.п.
Металлы являются поликристаллическими телами, состоящими из большого
количества зерен, размеры которых очень малы (порядка 0,01 мм).
Каждое зерно является анизотропным, но вследствие малых размеров зерен
и беспорядочного их расположения металлы проявляют свойство изотропии.

идеальной упругости, вследствие которой деформируемое тело полностью восстанавливает свою форму

и размеры после снятия нагрузки независимо от величин нагрузок и температуры тела.
4. Форма и размеры упругого тела меняются прямо пропорционально изменению нагрузок, то есть подчиняется закону Гука (1660 г.).

5. Материал обладает свойством сплошности, то есть способностью сплошь (без пустот) заполнять пространство, ограниченное
поверхностью тела. Вследствие этого материал считается непрерывным, что позволяет использовать для определения напряжений и деформаций
математический аппарат дифференциального и интегрального исчисления.
6. Упругие тела являются относительно жесткими, благодаря чему перемещения точек тела весьма малы по сравнению с размерами
самого тела. Эта гипотеза служит основанием для использования при расчете начальных (исходных) размеров тела (по недеформированной схеме).

Схематизация геометрии реального объекта – упрощает геометрию реально существующих тел, составляющих конструкцию.
Большинство сооружений, механизмов и машин можно расчленить на отдельные тела простой геометрической формы:
Брус - тело, два измерения которого малы по сравнению с третьим (стержни, стойки, валы, балки). Брус может иметь различную форму поперечного сечения (круглое, кольцевое, прямоугольное, коробчатое, двутавровое и др.). Поперечное сечение образуется при разрезе бруса плоскостью, перпендикулярной продольной оси, а продольная ось является линией, соединяющей центры тяжести поперечных сечений, и может быть прямой или криволинейной. Брус является основным объектом рассмотрения в курсе сопротивления материалов.
Следующие тела являются объектами рассмотрения в других разделах механики твердого деформируемого тела (теория пластин и оболочек, теория упругости и др.):
Оболочка, пластина - тело, одно измерение которого мало по сравнению с двумя другими (тонкостенные резервуары, оболочки перекрытия, плиты, стенки).
Массив - тело, все три измерения которого мало отличаются друг от друга (фундаментные блоки, шарик подшипника,
тело гравитационной плотины).

Схематизация силового воздействия – представляет модель механического действия внешних сил на объект
от других тел или сред. К внешним силам относятся также и реакции связей, определяемые методами теоретической механики.
Схематизация силового воздействия сводится к рассмотрению трех типов нагрузки:
Сосредоточенная сила – сила, рассматриваемая в курсе теоретической механики как вектор, характеризуемый модулем (величиной),
направлением действия и точкой приложения. Здесь такая сила является условной, поскольку механическое взаимодействие деформируемых тел
не может осуществляться в точке (площадь контакта не равна нулю). Условность состоит в том, что в случае малости площадки контакта по
сравнению с размерами объекта, сила считается приложенной в точке. Если же определяются контактные напряжения, например, в головке
рельса, то учитывается фактическое распределение нагрузки на рельс по площадке контакта, размеры которой зависят от величины сжимающей
силы (равнодействующей давления). Сосредоточенная сила измеряется в ньютонах (Н).
Объемные силы – силы, распределенные по объему (силы тяжести, силы инерции), приложенные к каждой частице объема. Для этих сил
схематизация часто состоит в задании простого закона изменения этих сил по объему.
Объемные силы определяются их интенсивностью, как предел отношения равнодействующей
сил в рассматриваемом элементарном объеме к величине этого объема, стремящего к нулю: и измеряются в Н/м3.

или другого тела), характеризуемые
интенсивностью давления, как предел отношения равнодействующей
сил на

рассматриваемой элементарной площадке к величине площади
этой площадки, стремящейся к нулю:

и измеряются в Н/м2.
Для этих сил схематизация часто
состоит в задании простого закона
изменения этих сил по поверхности.

Линейно распределенная нагрузка – силы, распределенные по некоторой
линии (длине), характеризуемая интенсивностью нагружения, как предел
отношения равнодействующей сил на рассматриваемой элементарной
длине линии к величине длины этой линии,
стремящейся к нулю:

и измеряются в Н/м.
Для этих сил условность состоит
в представлении области контакта
в виде линии нулевой толщины.
Характер изменения часто задается
в виде простого закона (постоянного, линейного).

По характеру воздействия на сооружения внешние силы делятся на статические и динамические. Динамическая нагрузка быстро изменяется
во времени (при движении подвижного состава, колебания, удар). При медленном изменении нагрузки можно пренебречь силами инерции и
деформациями, возникающими в объекте, и такая нагрузка может условно считаться статической. По времени действия на сооружения нагрузки
делятся на постоянные (вес пролетного строения, вес мостового полотна) и временные (нагрузка от проходящего подвижного состава, ветровая
или снеговая нагрузка). Временные нагрузки регламентируются специальными документами (СНиП, ТУ).

Внутренние силы – Под действием внешних сил на объект происходит изменение расстояний между частицами (атомами) рассматриваемого тела и сил взаимодействия между ними. В результате возникают так называемые внутренние силы, которые можно определить методом сечений:

F3

F4

1. Пусть брус под действием сил F1,F2, … находится
в равновесии. Для рассматриваемого объекта
удовлетворяются уравнения равновесия:

2. Проведем сечение плоскостью, совпадающей
с поперечным сечением бруса, в котором отыскиваются
внутренние силы.

3. Отбросим одну из частей (например, левую) и заменим ее действие на оставшуюся часть бруса
совокупностью реактивных сил, распределенных некоторым образом по поверхности поперечного
сечения.

4. Полученную систему внутренних сил можно упростить приведением к главному вектору и главному моменту, выбрав в качестве центра приведения центр тяжести поперечного сечения.

5. Разложим главный вектор и главный момент на составляющие по осям x, y, z: Rx, Ry, Rz и Mx, My, Mz.

z

x

y

O

R

Rx

Ry

Rz

M0

Mz

Mx

My

6. Полученные компоненты имеют в сопротивлении материалов специальные названия, соответствующие видам деформации:
Rz = N – нормальная сила, Rx = Qx, Ry = Qy – поперечные силы и Mz – крутящий момент, Mx, My – изгибающие моменты.

N

Qy

Qx

7. Поскольку оставленная часть бруса должна остаться в равновесии, полученные внутренние силовые факторы могут быть определены:
из уравнений равновесия, составленных для этой части:

Или, как легко можно доказать:

– мера, характеризующая распределение внутренних сил по сечению.
Поскольку внутренние

силы, представляют собой поверхностные силы, приложенные к поперечному сечению
оставленной части, то интенсивность этих сил, называемое полным напряжением, определяется как указано ранее:
Размерность этого напряжения совпадает с размерностью поверхностной нагрузки (Н/м2, МПа = 106 Н/м2).

Полное напряжение, как и равнодействующая внутренних сил, приложенных на элементарной площадке, является векторной величиной
и может быть разложено на две составляющие: перпендикулярное к рассматриваемой площадке – нормальное напряжение σn и
касательное к площадке – касательное напряжение n:

p

σn

n

n

Касательное напряжение, в свою очередь, может быть разложено на две составляющие,
параллельные координатным осям x, y, связанным с поперечным сечением - nx , ny :

ny

nx

z

x

y

При анализе напряжений в окрестности рассматриваемой точки выделяется бесконечно малый
объемный элемент (параллелепипед со сторонами dx, dy, dz), по каждой грани которого действуют,
в общем случае, три напряжения, например, для грани, перпендикулярной оси x (площадка x) – σx, xy, xz :

x

y

z

σz

zy

zx

σx

σy

xy

xz

yz

yx

Компоненты напряжений по трем перпендикулярным граням элемента образуют
систему напряжений, описываемую так называемым тензором напряжений:

Здесь первый столбец представляет компоненты напряжений на площадках,
нормальных к оси x, второй и третий – к оси y и z соответственно. Первый
индекс указывает площадку (“место”) действия, второй – направление. Для
нормальных напряжений индексы совпадают и один индекс опускается.

Связь внутренних усилий и напряжений – Внутренние усилия в сечении, как было показано выше,
связаны уравнениями равновесия с внешними силами, приложенными к оставленной части бруса при его сечении. С другой стороны внутренние усилия есть результат приведения к центру поперечного сечения внутренних сил, приложенных к элементарным площадкам (напряжений), выполняемое сложением, которое для элементарных сил сводится к интегрированию по площади поперечного сечения.

x

y

Выполнение этой операции
для каждого из внутренних усилий
приводит к следующим
интегральным выражениям:

σz

zy

zx

O

x

y

z

N

Qy

Qx

Mz

Mx

My

Таким образом, в целом связь внешних сил, внутренних усилий и напряжений такова:

Внешние силы

Внутренние усилия

Напряжения

Уравнения равновесия

Интегральные соотношения

Напомним, что опорные реакции конструкции включаются в число внешних сил.
Для определения этих реакций в статически неопределимых системах уравнений
равновесия недостаточно и следует дополнительно рассматривать перемещения,
связанные с внутренними усилиями и напряжениями, а также физические соотношения
упругости.
Задача определения напряжений в силу интегральности соотношений с внутренними
усилиями всегда статические неопределима и необходимо дополнительно рассматривать
деформации тела с целью определения закона распределения напряжений по сечению.

формы и размеров тела под действием нагрузки.
Полное перемещение точки в

пространстве раскладывается на компоненты u, v и w, параллельные осям x, y и z, соответственно.
Перемещения рассматриваемой точки зависит от деформации всех нагруженных областей тела и включают в себя перемещения как жесткого
целого ненагруженных областей. Таким образом, перемещения не могут характеризовать степень деформирования в окрестности
рассматриваемой точки.
■ Деформация в точке – мера деформирования материала в ее окрестности. Выделим в рассматриваемой точке тела элементарный
объем (параллелепипед со сторонами dx, dy, dz) и рассмотрим его возможные изменения размеров и формы.

y

z

x

Пусть за счет деформации длины его ребер получат абсолютные удлинения dx, dy и dz:

dx

dz

dy

dx

dz

dy

Относительные линейные деформации в точке:

Кроме линейных деформаций, связанных с изменением размеров линейных элементов возникают угловые деформации или
углы сдвига, связанные с изменением формы.
Например, в плоскости xy могут возникать малые
изменения первоначально прямых углов параллелепипеда:

Такие угловые деформации в общем случае могут иметь место во всех трех
плоскостях. Все относительные деформации весьма малы и имеют для реальных
материалов порядок ≈10-4-10-3.
Таким образом, совокупность относительных линейных и угловых деформаций определяют деформированное
состояние в точке и образуют тензор деформаций, подобный тензору напряжений:
Примечание: Половинные углы сдвига используются в целях получения аналогичных формул преобразования с тензором напряжений.

В зависимости от того, какие из компонент относительных деформаций имеют нулевое значение
в рассматриваемой области или для всего тела различают следующие простые виды деформаций:
Линейная деформация – εz ≠ 0, углы сдвига равны нулю, остальными линейными относительными деформациями пренебрегается
(характеризуется абсолютным и относительным удлинением).
Плоская деформация – εz ≠ 0, εx ≠ 0 или εy ≠ 0, остальные относительные деформации равны нулю (характеризуется абсолютным и
относительным сужением площади поперечного сечения). Эти виды деформаций обычно реализуются при растяжении-сжатии.
Объемная деформация – εz ≠ 0, εx ≠ 0, εy ≠ 0, углы сдвига равны нулю(характеризуется абсолютным и относительным изменением объема).
Чистый сдвиг – линейные относительные деформации равны нулю, углы сдвига не равны нулю (характеризуется изменением формы,
изменение объема не происходит). Это вид деформации также возникает при кручении.
В соответствии с видом деформации вначале последовательно изучают такие простейшие напряженно-деформированные состояния как
растяжение-сжатие, чистый сдвиг и кручение, чистый изгиб. Далее изучаются более сложные – поперечный изгиб, сложное сопротивление,
продольный изгиб.

усилия, вызывающие в них деформации растяжения или сжатия (стойки, элементы

ферм, тяги, тросы и т.п.). При этом в местах приложения условно сосредоточенных сил характер распределения деформаций достаточно сложный и отличается от распределения деформаций на удалении от этой локальной области. Размер этой области равен примерно наибольшему из размеров поперечного сечения.
Принцип Сен-Венана - Если совокупность некоторых сил, приложенных к небольшой части поверхности тела, заменить статически эквивалентной системой других сил, то такая замена не вызовет существенных изменений в условиях нагружения частей тела, достаточно удаленных от мест приложения исходной системы сил.
Как показывает опыт, за пределами этой области деформации практически постоянны и поперечные сечения перемещаются параллельно своим начальным положениям. На основании этого вводится гипотеза плоских сечений (Я. Бернулли):
Поперечные сечения стержня, плоские и перпендикулярные оси стержня до деформации, остаются плоскими и перпендикулярными после деформации.

Напряжения и деформации – Как было ранее сказано, задача определения напряжений всегда является статически неопределимой.
Такие задачи решаются последовательным рассмотрением статической, геометрической и физической сторон.
В данном случае имеем статическое уравнение, связывающее внутреннее усилие – продольную силу с напряжением:.

Для вычисления интеграла необходимо знать закон изменения напряжений по сечению. Этот закон можно установить
изучением непосредственно наблюдаемых перемещений (деформаций). Поскольку принимается гипотеза плоских сечений, то при отсутствии
внешней распределенной продольной нагрузки деформации постоянны по сечению и по длине стержня (геометрия) . Из введенного ранее
определения деформаций в точке :

где l – абсолютная продольная деформация (удлинение), l - длина (базовая длина) стержня.

Опытным путем установлена фундаментальная (физическая) связь усилий и удлинений (Р. Гук) и в дальнейшем, напряжений и деформаций (Коши, Навье) в виде:

где Е – модуль упругости (физическая постоянная материала, определяемая экспериментально).

Подстановка последнего соотношения – закона Гука в интегральное выражение c учетом постоянства деформации и напряжения дает:

Нормальное напряжение в поперечном сечении прямо пропорционально величине продольного усилия и обратно пропорционально площади сечения.

Абсолютную деформацию (удлинение) стержня также можно определить через продольное усилие:

Формула для абсолютного удлинения справедлива лишь при постоянной по длине стержня продольной силе
и неизменной площади поперечного сечения! В случае переменной продольной силы, например, при учете собственного
веса вертикальных стержней, и/или переменной площади необходимо использовать интегральное выражение:

Центральное растяжение-сжатие. Принцип Сен-Венана. Напряжения и деформации. Коэффициент Пуассона. Закон Гука. Модуль упругости. Напряжения на наклонных площадках. Внутренние усилия при растяжении-сжатии.

сечении стержня возникает лишь один силовой
фактор – продольная сила N.

В соответствии с методом сечений величина и направление продольной силы может быть найдены из
уравнения равновесия в проекции на ось, совпадающую с осью стержня, составленного для оставленной части:

Продольная сила считается положительной, если она вызывает растяжение, т.е. направлена от сечения (в сторону внешней нормали), и отрицательной, если она вызывает сжатие, т.е. направлено к сечению.

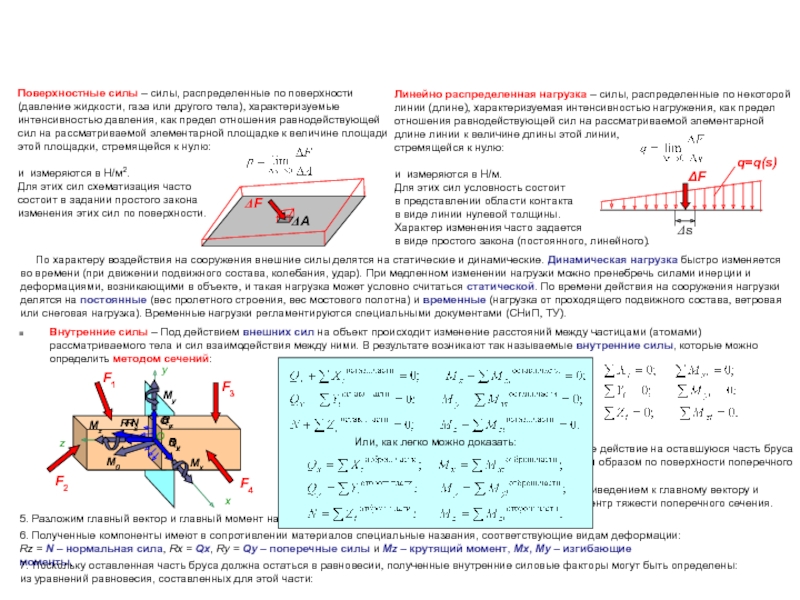
■ Определение внутренних усилий – Внутренние усилия определяются методом сечений в совокупности точек по длине бруса с целью
обнаружения их максимальных значений. График изменения внутреннего усилия по оси бруса называется эпюрой.
Общий порядок построения эпюр внутренних усилий:
Если необходимо, то определяются опорные реакции так, как это делается в курсе теоретической механики (выбрать объект, отбросить
связи, заменить отброшенные связи реакциями, составить уравнения равновесия). Реакции можно не находить, если они не входят в число
внешних сил, приложенных по одну сторону от рассматриваемых сечений.
Определяется число участков по длине бруса, на которых нагрузка или геометрия бруса не изменяется. Границей участка является любой
фактор, влияющий на резкое (скачкообразное) изменение рассматриваемого внутреннего усилия (начало или конец бруса, перелом оси бруса,
место расположения опоры, точка приложения внешней сосредоточенной силы или другого фактора, например, сосредоточенного момента,
начало или конец распределенной нагрузки).
На каждом из участков проводится сечение, отстоящее от начала участка на некотором произвольном (переменном) расстоянии. Для
каждого сечения указывается текущая координата (z) от начала участка или от начала бруса и записываются пределы изменения координаты.
При выборе начала локальных координат в начале участка нижний предел всегда равен нулю.
Для рассматриваемого сечения определяется выражение внутреннего усилия в функции от координаты z рассмотрением равновесия
оставленной части или используя установленные определения для вычисления внутреннего усилия по внешним силам, расположенным по одну
сторону от сечения.
По полученным выражениям строится эпюра изменения усилия подстановкой верхнего и нижнего пределов, и если необходимо,
других значений координат в разрешенном интервале, обычно в середине интервала.

Пусть прямолинейный брус нагружен продольными силами F1, F2:

Реакции левой опоры можно не определять, т.к. в этом примере можно ограничиться рассмотрением
лишь сил, приложенных к правым оставленным частям (справа от сечений).

2. Число участков - 3

3. Проведем сечение I-I на первом участке и определим текущую координату сечения и пределы ее
изменения: 0  z1  a.

4. Отбросим левую часть, заменим ее действие продольной силой NI-I
и составим уравнение равновесия в проекции на ось z :

NI-I

Из уравнения равновесия получаем выражение для продольной силы на участке 1 :

Повторяем шаги 3 и 4 для следующих участков:

3. Проведем сечение II-II на втором участке и определим текущую координату сечения и пределы ее
изменения: 0  z2  b.

4. Отбросим левую часть, заменим ее действие продольной силой NII-II
и составим уравнение равновесия в проекции на ось z :

NII-II

Из уравнения равновесия получаем выражение для продольной силы на участке 2 :

Аналогично получаем для участка 3 (0  z3  c):

Полученные выражения показывают, что продольная сила в сечении равна алгебраической сумме
проекций на ось бруса сил, взятых по одну сторону от сечения!

Знак слагаемых положителен, если рассматриваемая сила направлена
от сечения, т.е. будучи приложена к сечению вызывает растяжение части бруса по другую сторону
от сечения.

Используя полученные выражения для продольной силы построим эпюру продольных сил:
При построении эпюры N, положительные значения обычно откладываются вверх от базисной линии
или вправо, если она вертикальна.
Пусть F1=250 кН, F2=100 кН. Откладывая не каждом из участков значения продольной силы в некотором
выбранном масштабе получаем эпюру N:

Обратите внимание, что скачки на эпюре N располагаются в точках приложения внешних
сосредоточенных сил и равны величинам этих сил. Соответственно скачок на левом конце
эпюры дает величину опорной реакции.

(удлинением), определяемой законом Гука,
возникает поперечная деформация (сужение поперечного сечения), выражающаяся

в уменьшении поперечных размеров стержня.
Относительные поперечные деформации вычисляются как где b, h – размеры поперечного сечения.

Экспериментально установлено, что имеется линейная связь
между продольной и поперечной деформацией: где μ – коэффициент пропорциональности, называемый
коэффициентом Пуассона.
Коэффициент Пуассона для данного материала в пределах упругих деформаций имеет постоянное значение
и находится в пределах от 0 до 0,5.

По закону Гука, определяющему связь нормальных напряжений с продольными деформациями:
Тогда

Как упоминалось ранее, в общем случае нагружения по граням выделенного
элемента возникают нормальные и касательные напряжения. Последние,
вызывая деформации сдвига, не влияют на линейные деформации,
поскольку не изменяют длин сторон элемента. Используя принцип независимости
действия сил, справедливый для изотропного и линейно упругого материала,
можно записать обобщенный закон Гука, учитывающий одновременное действие
нормальных напряжений по всем граням элемента:

Напряжения по наклонным площадкам – При растяжении стержня в его
поперечном сечении возникают только нормальные напряжения. Посмотрим
какие напряжения возникают в сечении, не перпендикулярном оси стержня.



1. Отбросим правую часть и заменим ее действие главным вектором внутренних сил R :
Из уравнения равновесия в проекции на ось стержня R = F.

R

2. Разложим это внутреннее усилие на нормальную и касательную к сечению составляющие N и Q:

N

Q



3. Вычислим нормальные и
касательные напряжения
по наклонному сечению
площадью A =A/cos:

Здесь по-прежнему предполагается равномерное распределение напряжений по сечению.

С учетом того, продольная сила N в поперечном сечении равна внешней растягивающей силе F, отношение F/A = N/A есть нормальное напряжение в поперечном сечении. Тогда получаем:

Анализ полученных соотношений показывает:
1. При  = 0 (наклонная площадка совпадает с поперечным сечением):
Касательные напряжения отсутствуют, а нормальные напряжения
максимальны.
2. При  = 45о касательные напряжения максимальны,
а нормальные напряжения равны касательным.

3. При  = 90о (продольная площадка) нормальные и касательные напряжения обращаются
в ноль (продольные волокна не давят друг на друга и не сдвигаются).
4. На двух взаимно перпендикулярных площадках касательные напряжения
равны по абсолютной величине.

F. Выделим на расстоянии z участок длиной dz. Удлинение этого

участка dz равно перемещению второй его границы относительно первой dw.
Деформация на этом участке определяется выражением,
представляющим собой дифференциальное уравнение:

Разделим переменные и сведем решение этого уравнения
к интегрированию левой и правой частей:

Подставим пределы и выражение для деформации,
следующего из закона Гука:

Здесь w0 – перемещение левой границы рассматриваемого участка на расстоянии z0, EA – жесткость стержня при растяжении-сжатии,
N – продольное усилие.

В случае постоянства продольного усилия и площади поперечного сечения имеем:

Отсюда, как частный случай, получается выражение для абсолютного удлинения стержня (w0 = 0, z0 = 0, z = l):

Общая формула вычисления перемещений показывает, что перемещения исчисляются нарастающим итогом, т.е. к перемещению, вычисляемому
на рассматриваемом участке [z0 ,z] (второе слагаемое), добавляется перемещение сечения, соответствующего левой границе, и представляющего
перемещение всего участка, как жесткого целого (твердого тела). Если на каждом из участков продольное усилие и площадь поперечного сечения постоянны, то определение перемещения любого сечения или конца стержня сводится к простому суммированию удлинений каждого
из участков от неподвижного сечения до рассматриваемого.

Учет собственного веса – Рассмотрим стержень, нагруженный собственным весом (длина стержня l, объемный вес материала стержня ).

Продольное усилие от собственного веса в произвольном сечении на расстоянии z равно весу нижерасположенной части стержня
и линейно зависит от координаты. Эпюры продольной силы и нормальных напряжений имеют вид треугольников:

Перемещение произвольного сечения на расстоянии z имеет квадратичную зависимость от координаты:

Определим перемещения конца стержня и сечения на расстоянии половины длины:

Здесь G – вес стержня.

Таким образом, учет равномерно распределенной продольной нагрузки (собственный веса) может быть
выполнен непосредственным интегрированием по рассматриваемому участку или использованием
выражения, подобного абсолютному удлинению стержня при постоянной продольной силе,
в котором сила уменьшена вдвое! (см. результат определения перемещения конца стержня).

Например, второй результат (перемещение сечения посредине длины стержня) может быть получен,
как сумма перемещений рассматриваемого сечения стержня от действия собственного веса верхней
части, учитываемого как распределенная нагрузка, и перемещения его от веса нижней части,
действующего на верхнюю часть как внешняя сила:

Перемещения при растяжении сжатии. Учет собственного веса. Статически неопределимые системы при растяжении сжатии.

число наложенных связей больше числа независимых уравнений равновесия. Как указывалось

выше, такие задачи решаются последовательным рассмотрением статической, геометрической и физической сторон, в результате чего получается полная система уравнений, позволяющая найти искомые усилия. Общий порядок решения определяется вышесказанным, конкретные шаги и особенности рассмотрим на примерах:
Пример 1. Стержень переменного сечения (2A и A) жестко заделан с двух сторон и нагружен продольной силой. Построить эпюры N и σ.

1. Выбираем объект равновесия, отбрасываем связи и заменяем их действие реакциями:

RA

RB

2. Статика : Составляем уравнение равновесия:

Это единственное уравнение равновесия, которое можно составить для линейной системы сил.
Следовательно система один раз статически неопределима.

3. Геометрия:
Составляем уравнение совместности деформаций:

Это уравнение устанавливает неизменность общей длины стержня при любых воздействиях, которую обеспечивали связи (жесткие заделки) до их удаления.

4. Физика: Записываем соотношения связи деформаций с усилиями:

Получили полную систему уравнений, решающую данную задачу (5 уравнений и 5 неизвестных – 2 реакции и 3 перемещения) .

Такой же результат можно получить с использованием статически определимой
системы, образованной из заданной статически неопределимой отбрасыванием
“лишней” связи, и принципа независимости действия сил:

RB

Подставим полученное соотношение
в уравнение равновесия:

Это уравнение устанавливает неизменность общей длины стержня, которую обеспечивала “лишняя” связь (правая жесткая заделка) до ее удаления, или равенство перемещений и их противоположное направление при отдельном действии внешней нагрузки и реакции этой связи.

или

Записываем соотношения связи деформаций
(перемещений) с усилиями:

Получили полную систему уравнений, решающую данную задачу
(4 уравнения и 4 неизвестных – 2 реакции и 2 перемещения) .

Подставляем соотношения упругости в уравнения совместности:

Составляем уравнение совместности деформаций:

Подставим полученное соотношение
в уравнение равновесия и получим
величину второй реакции (RB).

Подставляем перемещения в уравнения совместности:

Эпюра нормальных напряжений также строится
вычислением значений напряжений по участкам:
σ1 = N1 / A1= 3F/8A,
σ2 = N2 / A2= F/8A,
σ3 = N3 / A3= F/4A.
В сечении резкого изменения площади получился скачок.

Если имелся первоначальный зазор, например между правым концом
стержня и заделкой, или напротив натяг (первоначальный размер стержня
превышает расстояние между опорами), то это учитывается лишь
в уравнениях совместности деформаций:
или (>0 зазор, <0 натяг)

Если вместо силового нагружения, или дополнительно к нему, действует
температурная нагрузка (нагрев), то это учитывается введением
температурных удлинений в уравнения совместности деформаций.

машин и механизмов необходимо знать прочностные и деформационные свойства материалов.

Их определяют экспериментально на специальных испытательных машинах. Из всех прочих свойств (твердость, сопротивляемость ударным нагрузкам, противодействие высоким или низким температурам и т.п.) основными является сопротивление на растяжение и сжатие, дающие наибольшую и важнейшую информацию о механических свойствах металлов.
Испытание на растяжение – проводят на разрывных или универсальных машинах, имеющих специальные
захваты для передачи усилия. Используются стандартные образцы специальной формы
(l0 – длина рабочей части, l0/ a0 = 5 – короткие, l0/ a0 = 10 – длинные):

При испытаниях на сжатие применяются цилиндрические образцы
с отношением высоты к диаметру h/d = 1,5 – 3.
Образцы устанавливаются на опорную поверхность
с использованием смазки для ослабления влияния
сил трения.

Диаграммы растяжения пластичных и хрупких материалов – Характерной
диаграммой пластичных материалов является диаграмма растяжения низкоуглеродистой
стали (< 0,25% С):

Все машины снабжены устройством для автоматической записи
в определенном масштабе диаграммы-графика зависимости величины
растягивающей силы от удлинения образца.
Современные машины компьтеризированы и имеют средства управления процессом
нагружения по различным задаваемым программам, вывода данных на экран
и сохранения их в файлах для последующей обработки:

1. В начальной стадии (OA, до Fпц) нагружения удлинение
растет прямопропорционально величине нагрузки
(на этой стадии справедлив закон Гука):

O

A

2. Далее (AB, до Fуп) деформации начинают расти чуть
быстрее и не линейно, но остаются малыми и упругими
(исчезающими после снятия нагрузки).

B

3. При дальнейшем нагружении (BС, до Fт) криволинейная часть переходит
в горизонтальную площадку CD, на которой деформации растут без увеличения
нагрузки (текучесть). Зона BCD – зона общей текучести.

С

D

4. При дальнейшем нагружении (DE, до Fмакс) изменяется структура металла и материал
вновь может воспринимать возрастание нагрузки (упрочнение) вплоть до максимальной.

E

5. Далее (EK, до Fк) в наиболее слабом месте возникает и развивается локальное
уменьшение поперечного сечения (шейка). Зона EK – зона местной текучести.

K

Fк

В точке K образец внезапно разрушается
с резким ударным звуком, но без световых эффектов.

Испытание материалов на растяжение-сжатие. Характеристики прочности и пластичности. Идеализированные диаграммы. Потенциальная энергия деформации (полная, удельная).

связывающая нагрузку с удлинением не может непосредственно характеризовать прочность и

пластичность материала, поскольку нагрузка зависит от площади поперечного сечения образца, а удлинение – от базовой его длины. Для получения объективных механических характеристик материала, не зависящих от сечения и длины образца, необходимо перейти к напряжениям и относительным удлинениям. Для этого нагрузка делится на начальную или текущую площадь поперечного сечения образца, а по оси абсцисс откладывается соответствующее относительное удлинение для каждой их характерных точек.

В результате получается диаграмма напряжений, подобная диаграмме растяжения:

В этой диаграмме характерные точки определяют следующие механические свойства
материала:
1. Предел пропорциональности σпц – наибольшее напряжение, до которого
существует пропорциональная зависимость между нагрузкой и деформацией
(для Ст3 σпц =195-200 МПа).

2. Предел упругости σуп – наибольшее напряжение, при котором в материале
не обнаруживается признаков пластической (остаточной) деформации
(для Ст3 σуп =205-210 МПа).

3. Предел текучести σт – наименьшее напряжение, при котором образец
деформируется без заметного увеличения растягивающей нагрузки
(для Ст3 σт =220-250 МПа).

4. Предел прочности или временное сопротивление σв – напряжение,
соответствующее наибольшей нагрузке, предшествующей разрушению
образца (для Ст3 σв =370-470 МПа).

5. Истинный предел прочности или истинное сопротивление разрыву σи
– напряжение, соответствующее разрушающей силе FK, вычисленное для
площади поперечного сечения образца в месте разрыва A1 (для Ст3
σв =900-1000 МПа). Поскольку на участке EK образуется шейка и площадь
поперечного сечения быстро уменьшается, напряжение увеличивается (EK1)
при регистрируемом падении усилия.

Механизм разрушения: в области шейки образуются мелкие продольные трещины,
которые затем сливаются в одну центральную трещину, перпендикулярную оси растяжения,
далее трещина распространяется к поверхности шейки, разворачиваясь примерно на 450,
и при выходе на поверхность образует коническую часть излома.
В результате получается поверхность излома в виде “конуса” и “чашечки”. Стадия
образования конической поверхности показывает, что материал в вершине трещины
начинает разрушаться по механизму скольжения (по площадкам максимальных
касательных напряжений), характерному для хрупких материалов.

при его сопротивлении переменным динамическим нагрузкам, а также технологическим свойством

при его обработке (штамповка и др.).
К характеристикам пластичности относятся:

1. Относительное удлинение после разрыва  (%) – отношение
приращения расчетной длины образца после разрыва к ее
первоначальному значению (для Ст3  = 25-27 %).

2. Относительное сужение после разрыва ψ (%) – отношение
уменьшения площади поперечного сечения образца
в месте разрыва к начальной площади поперечного
сечения (для Ст3 ψ =60-70 %).

Идеализированные диаграммы – При решении статически неопределимых задач
рассматривается физическая сторона задачи, в которой необходимо иметь
аналитическую зависимость между напряжениями и деформациями. Такую зависимость,
представляемой полученной экспериментально диаграммой напряжений, сложно
получить в аналитическом виде и использовать в расчетах.

lK

В связи с этим используются упрощенные (идеализированные) диаграммы, отражающие
основные закономерности. В частности, для пластичных материалов часто применяется
диаграмма Прандтля, состоящая всего из двух прямолинейных участков.
Как видно, диаграмма Прандтля распространяет зону действия закона Гука до предела
текучести, после чего предполагается (задается), что материал испытывает далее
текучесть вплоть до разрушения.

ε

Потенциальная энергия деформации – Эта величина характеризует способность
материала совершить работу при переходе его из деформированного состояния
в исходное. При деформации внешние силы совершают работу W, которая превращается
в потенциальную энергию внутренних упругих сил U (например, при сжатии пружины).
При снятии нагрузки внутренние силы возвращают материал в исходное
(недеформированное) состояние (пружина распрямляется).
Таким образом, для упругих материалов процесс полностью обратим:

При статическом растяжении образца силой F
элементарная работа на малом перемещении
равна:

dl

Полная работа равна:

- площадь, ограниченная кривой растяжения

В пределах соблюдения закона Гука потенциальная энергия деформации равна:

l

В случае переменной величины продольной силы и/или площади поперечного сечения по длине стержня:

Таким образом, удельная потенциальная энергия численно равна площади треугольника на диаграмме напряжений ( в пределах соблюдения закона Гука).

отличается от его поведения при растяжении.
Диаграмма низкоуглеродистой стали –

Начальный участок диаграммы является прямолинейным ( до точки A) и совпадает с аналогичным участком диаграммы растяжения. Это свидетельствует о том, что модуль упругости у стали можно принимать одинаковым при растяжении и сжатии. Нелинейный участок до площадки текучести также совпадает с подобным участком на диаграмме растяжения.
Значения предела пропорциональности и предела текучести при растяжении и сжатии практически одинаковы. Площадка текучести при сжатии выражена очень слабо и после нее кривая уходит все более круто вверх вследствие развития значительных пластических деформаций, приводящих к увеличению площади поперечного сечения. Образец сплющивается принимая бочкообразную форму.
На этом испытания заканчивают, т.к. образец разрушить не удастся, не удается определить и
предел прочности.

■ Диаграмма чугуна – Начальный участок диаграммы имеет почти линейную зависимость,
на этом участке форма и размеры образца меняются незначительно. При приближении
к максимальной нагрузке кривая становится более пологой и образец принимает слегка
бочкообразную форму. При достижении нагрузкой наибольшего значения появляются трещины
под углом примерно 450 и наступает разрушение по площадкам с наибольшими касательными
напряжениями (хрупкое разрушение).
Другие хрупкие материалы (камень, бетон) имеют подобную диаграмму и такой характер
разрушения. Хрупкие материалы сопротивляются сжатию значительно лучше, чем растяжению,
например, предел прочности серого чугуна на сжатие 560-900 МПа, а на растяжение – 120-190 МПа.

■ Диаграмма древесины – Древесина – анизотропный материал. Сопротивляемость при сжатии
зависит от расположения волокон относительно направления сжимающей силы.
При сжатии вдоль волокон на участке OA древесина работает почти упруго, деформации растут
пропорционально увеличению сжимающей силы. Далее деформации начинают расти более быстро,
чем усилие, вследствие возникновения пластических деформаций в отдельных волокнах.
Разрушение происходит при максимальной нагрузке в результате потери местной устойчивости
ряда волокон, сопровождаемой сдвигом с образованием продольных трещин.

При сжатии поперек волокон на участке OB древесина работает почти упруго,
деформации растут пропорционально увеличению сжимающей силы. Далее
деформации начинают расти очень быстро при малом увеличении силы, вследствие
уплотнения (спрессовывания) отдельных волокон. При наличии сучков и других
пороков (трещин) образец может разрушиться раскалыванием.
Разрушающая нагрузка определяется условно при достижении деформации сжатия,
при которой высота образца уменьшается на треть исходной высоты .

B

Диаграмма сжатия. Основные механические характеристики. Особенности разрушения пластических и хрупких материалов при растяжении-сжатии малоуглеродистой стали и чугуна.

состояний – Основной задачей расчета конструкции является обеспечение ее прочности

в условиях эксплуатации. Прочность конструкции, выполненной из хрупких материалов, считается обеспеченной, если во всех поперечных сечениях фактические напряжения меньше предела прочности материала. Величины нагрузки, напряжения в конструкции и механические характеристики материала не могут быть установлены совершенно точно из-за того, что имеют место такие факторы, как случайный характер нагружения, приближенность расчета, погрешность испытаний, разброс механических свойств реальных материалов и т.д.
Поэтому необходимо, чтобы наибольшие напряжения, полученные в результате расчета (расчетные напряжения) не превышали некоторой величины, меньшей предела прочности. Эта величина называется допускаемым напряжением и устанавливается делением предела прочности на коэффициент, больший единицы, называемый коэффициентом запаса.
В соответствии с этим условие прочности:



где - наибольшие расчетные растягивающие и сжимающие напряжения в конструкции;

- допускаемые напряжения при растяжении и сжатии соответственно.

Итак, условие прочности по методу допускаемых напряжений
при проверке напряжений при растяжении-сжатии стержней имеет вид:

Допускаемые напряжения связаны с пределами прочности
на растяжение и сжатие отношениями:

где nВ – нормативный (требуемый) коэффициент запаса прочности по отношению к пределу прочности, определяемый в зависимости от класса конструкции (капитальная, временная и т.п.), от предполагаемого (задаваемого) срока службы, от характера нагрузки (статическая, динамическая и т.п.), от условий работы конструкции, от качества изготовления материалов и других факторов. Величина nВ в большинстве случаев принимается в диапазоне от 2, 5 до 5.

Для конструкций из пластических материалов, имеющих одинаковые
пределы прочности на растяжение и сжатие, условие прочности:

Допускаемые напряжения: где nТ – нормативный (требуемый) коэффициент запаса прочности по отношению
к пределу текучести (nТ = 1,5 – 2,5).

где max – наибольшие по абсолютной величине
сжимающие или растягивающие напряжения в конструкции.

При подборе сечения принимаемые сечения должны удовлетворять
неравенству, вытекающему из условия прочности:

При определении грузоподъемности вычисляется
допускаемая продольная сила
в наиболее нагруженном стержне:

По полученной допускаемой силе определяется далее величина
допускаемой нагрузки [F]. Условие прочности принимает вид:

Основные сведения о расчете конструкций. Методы допускаемых напряжений и предельных состояний.

опорной плоскости, так и по касательной (не препятствует повороту).

Реакция неподвижного
шарнира

проходит через центр шарнира перпендикулярно оси шарнира и имеет произвольное направление.

Реакцию неподвижного
шарнира можно разложить на две составляющие, например, Rx и Ry, параллельные координатным осям.

Другие схематические изображения
шарнирно-неподвижной опоры:

Жесткое защемление (жесткая заделка) – ограничивает как поступательные, так и вращательные движения (линейные и угловые перемещения) объекта. В случае плоской системы сил (плоская заделка)
ограничиваются перемещения по осям x, у и поворот в плоскости x, у.

В жесткой плоской заделке возникает три реактивных усилия: две составляющие реактивные силы RAx и RAy,
а также реактивный момент (пара сил) MA .

В сопротивлении материалов и далее в строительной механике горизонтальные и вертикальные реакции для сокращения наименования часто обозначают как HA (horizontal) и VA (vertical).
В случае пространственной системы сил возникают три реакции по направлению трех координатных осей и три реактивных момента (пар сил) относительно этих осей.

Схематизация опорных устройств – упрощает реальные конструкции опорных устройств с сохранением функций
ограничения перемещений. Схематизация большинства из опорных устройств рассмотрена в курсе теоретической механике
и сводится к к нескольким типам опор:
Шарнирно-подвижная (катковая) опора – ограничивает перемещение объекта
по нормали к опорной плоскости (не препятствует повороту и перемещению
по касательной к опорной плоскости).

Реакция подвижного
шарнира проходит через центр шарнира перпендикулярно оси шарнира и плоскости опирания.

Другие схематические изображения
шарнирно-подвижной опоры:

Основные типы опор и балок – Стержни, работающие главным образом на изгиб, называются балками. Балки являются простейшими
несущими конструкциями в мостах, промышленных и гражданских сооружениях. Балки опираются на другие конструкции или основание (стены,
колонны, устои и др.).

Основные типы балок – различаются способом закрепления:
Консоль – один конец жестко защемлен, второй свободен.
Простая (двух опорная) – по обоим концам шарнирные опоры.
Консольная (двух опорная) – простая балка с консольными частями.
Составная балка – составленная из двух или более простых, консольных балок и консолей.

Во всех случаях число связей должно быть достаточным для обеспечения неподвижности балки (плоские системы – 3, пространственные – 6)
и способы постановки связей должны исключать мгновенную изменяемость системы.
Примеры мгновенно-изменяемых систем:

A

Основные типы опор и балок. Чистый и поперечный изгиб. Внутренние усилия при изгибе. Дифференциальные зависимости. Построение эпюр поперечных сил и изгибающих моментов.

Уравнения равновесия могут быть составлены в виде одной из трех

форм:




Поскольку найденные опорные реакции участвуют в дальнейших расчетах (построение эпюр внутренних усилий, определение
напряжений и перемещений) следует активно пользоваться этими формами уравнений так, чтобы в каждое из уравнений входила лишь одна
определяемая реакция, чтобы исключить подстановку ранее найденных и не проверенных реакций. После независимого вычисления всех
реакций обязательно должна быть сделана проверка составлением такого уравнения равновесия, в котором бы присутствовали все или
большинство из найденных реакций. Поскольку балки несут преимущественно вертикальную нагрузку, то в общем случае рекомендуется
воспользоваться формой II и проверить вертикальные реакции составлением уравнения в проекциях на вертикальную ось.
Помните, что неверно найденные реакции в любом случае приведут к неверным результатам при построении эпюр, определении
напряжений и перемещений!

Внутренние усилия при изгибе – При изгибе возникают в общем случае изгибающие моменты Mx, My и поперечные силы Qx , Qy.
Если в поперечном сечении возникает только один изгибающий момент Mx, то такой изгиб называется чистым.
В большинстве случаев дополнительно к изгибающему моменту возникает поперечная сила Qy, и такой изгиб
называется поперечным.
Если внешняя нагрузка и реактивные усилия лежат в одной плоскости, то такой изгиб называется плоским.
Правила знаков для изгибающего момента – Изгибающий момент принимается положительным,
если он изгибает элемент балки так, нижние волокна оказываются растянутыми, т.е. ось балки искривляется
выпуклостью вниз.
Правила знаков для поперечной силы – Поперечная сила считается положительной, если она
стремится повернуть элемент балки по ходу часовой стрелки.

■ Дифференциальные зависимости при изгибе – связывают внутренние усилия между собой в сечении и нагрузкой. Выделим из балки элемент длиной dz, находящийся по действием внешней вертикальной равномерно распределенной нагрузкой q, и заменим действие отброшенных частей внутренними усилиями:

Выделенный элемент находится в равновесии
и удовлетворяет уравнения равновесия:

Из первого уравнения
получаем:

Производная от поперечной силы
по продольной координате равна
интенсивности распределенной нагрузки.

Из второго уравнения, пренебрегая малыми
второго порядка получаем:
Производная от изгибающего момента
по продольной координате равна поперечной силе.

не отличается от построения эпюры продольных сил и крутящих моментов.

Положительные значения поперечной силы Qy откладываются вверх от горизонтальной базовой линии, а отрицательные – вниз. Положительные значения изгибающих моментов Mx откладываются вниз – со стороны растянутого волокна. Таким образом расположение ординат эпюры Mx указывают, какие волокна растянуты.
Примечание: Это правило принято в строительных и транспортных вузах в то время, как в машиностроительных и авиационных вузах используется обратное правило (положительный момент откладывается со стороны сжатого волокна).

Пусть балка нагружена равномерно распределенной нагрузкой q, сосредоточенной силой F=qa и крутящим моментом M=qa2:

q

F

M

1. Определяем
опорные реакции:

HA

VA

VB

A

B

z

y

Из второго и третьего
уравнений получаем:

Выполняем контроль:

VB = 1,75qa

VA = 1,25qa

2. Количество участков – 3.

3. Проведем сечение I-I на первом участке и определим текущую координату сечения и пределы ее
изменения: 0  z1  2a.

4. Отбросим правую часть, заменим ее действие поперечной силой QyI-I и изгибающим моментом MxI-I
и составим уравнения равновесия в проекциях и в моментах относительно оси x, проходящей через
центр текущего сечения (т.е. относительно точки С) :

y

Отсюда получаем:

3. Проведем сечение II-II на втором участке и определим текущую координату сечения и пределы ее
изменения: 0  z2  2a.

Повторяем шаги 3 и 4 для следующих участков:

4. Отбросим правую часть, заменим ее действие поперечной силой QyII-II и изгибающим моментом MxII-II
и составим уравнения равновесия в проекциях и в моментах относительно оси x, проходящей через
центр текущего сечения (т.е. относительно точки D) :

Отсюда получаем:

Аналогично получаем для участка 3 (0  z3  2a):

Используя полученные выражения для поперечной силы и изгибающего момента построим эпюру поперечных сил и изгибающих моментов, подставляя значения реакций и координаты начала и конца участков. В случае квадратичного изменения величины (изгибающий момент на первом участке) дополнительно подставляется координата точки внутри интервала, например, посредине.
Откладывая не каждом из участков значения поперечных сил и изгибающего момента
в некотором выбранном масштабе получаем эпюры Qy и Mx:

Свойства эпюр:
1. Равномерно распределенная нагрузка на участке
своего действия вызывает на эпюре Q наклонную
прямую линию, падающую в сторону действия нагрузки,
а на эпюре M – параболу с выпуклостью в ту же сторону.
2. Сосредоточенная сила вызывает на эпюре Q
скачок в точке приложения силы в сторону действия силы,
а на эпюре М – перелом в ту же сторону.
3. Сосредоточенный момент не вызывает на эпюре Q
в точке его приложения никаких особенностей,
а на эпюре M вызывает скачок в ту же сторону.
Смотрите и удивляйтесь!

его оси) испытывают лишь деформации растяжения-сжатия
и не оказывают давления

друг на друга (гипотеза об отсутствии сдавливания продольных волокон).

Нормальные напряжения при чистом изгибе – Как указывалось ранее, задача определения напряжений является статически неопределимой, для решения которой необходимо последовательно рассмотреть три стороны задачи:

В общем случае балка может испытывать изгиб под действием изгибающих моментов относительно осей x и y.
Если один из них равен нулю, а другой лежит в главной плоскости сечения (плоскости, проходящей через ось стержня
и одну из главных центральных осей инерции) , то такой изгиб называется плоским изгибом. Если при этом изгибающий момент постоянный,
и это означает отсутствие поперечной силы, то такой изгиб называется чистым изгибом.

z

z

Mx

Mx

2. Каждое поперечное сечение стержня, плоское до деформаций, остается плоским и нормальным
к деформированной оси стержня после деформации (гипотеза плоских сечений).

Первая гипотеза пренебрегает влиянием нормальных напряжений σx и σy на продольную деформацию элемента,
вторая – деформациями сдвига. Обе гипотезы подтверждаются экспериментально на основной части длины стержня

1. Статика: Выделим малый элемент двумя нормальными к оси бруса сечниями и заменим действие
отброшенных частей нормальными напряжениями. Под их действием элемент находится в равновесии.

z

z

Ранее приведением распределенных сил к центру и центральным осям было получены интегральные
соотношения, связывающие нормальное усилие и изгибающий момент с нормальными напряжениями:

z

zdA

y

Из этих соотношений найти напряжения и положение нейтральной оси пока нельзя, поскольку закон изменения напряжений по высоте сечения неизвестен.

2. Геометрия: Согласно гипотезе плоских сечений, продольные волокна испытывают деформации
растяжения-сжатия, пропорциональные расстоянию от нейтральной оси. Нейтральная ось, как и
центральная ось стержня, изгибается и имеет радиус кривизны  (т. А – центр кривизны).

Mx

Так как нормальное усилие
при изгибе равно нулю, то:

Последнее указывает на то, что в сечении возникают напряжения разного знака и следует предполагать,
что существуют волокна, в которых напряжения равны нулю (нейтральная ось).

Абсолютное удлинение волокна, находящегося
на произвольном расстоянии от нейтральной
оси, из подобия треугольников равно:

A

3. Физика: По закону Гука:

Подставим напряжение
в выражение
для нормальной силы:

Таким образом, нормальное напряжение линейно зависит
от расстояния до нейтральной оси. При y0 > 0 – сжатие.

-

+

Этот интеграл представляет собой статический момент площади и равенство
его нулю означает, что нейтральная ось проходит через центр тяжести.

Подставим напряжение
в выражение для изгибающего
момента (y0  y ) :

Замечание: Знак минус учитывает правило
знаков для изгибающего момента и напряжений.

z0

= Ix

Изгиб балок. Основные допущения. Нормальные напряжения при чистом изгибе. Момент сопротивления при изгибе. Условие прочности по нормальным напряжениям. Понятие рационального сечения при изгибе.

напряжений при изгибе следует, что наибольшие (положительные – растягивающие) и

наименьшие (отрицательные – сжимающие) напряжения в поперечном сечении возникают в точках, наиболее удаленных от нейтральной оси, расположенных по обе стороны от нее:

При симметричном сечении относительно нейтральной оси абсолютные
величины наибольших растягивающих и сжимающих напряжений равны
и могут быть определены по формуле: В других случаях необходимо специально искать ymax , но формула остается в силе.

Величина, зависящая только от размеров и формы поперечного сечения, называется осевым моментом сопротивления:

Моментом сопротивления удобно пользоваться при расчете на прочность (подбор сечения) балки при изгибе.
Конечно для этого моменты сопротивления предварительно вычисляются для типовых и прокатных сечений по предыдущей формуле.

С использованием осевого момента сопротивления максимальные напряжения вычисляются как:

Момент сопротивления типовых и прокатных сечений:
1. Прямоугольное сечение:

2. Круглое сечение:

3. Для прокатных сечений все геометрические характеристики,
в том числе и моменты сопротивления, уже вычислены и содержатся
в специальных таблицах – сортаментах.

Во всех случаях, кроме круглого сечения, следует использовать моменты сопротивления, соответствующие ориентации
Плоскости действия изгибающего момента. Например, при действии на балку прямоугольного сечения момента My
при вычислении максимальных нормальных напряжений необходимо использовать Wy:

Условие прочности по нормальным напряжениям:

Максимальные напряжения не должны превышать
расчетных или допускаемых напряжений.

Отсюда при подборе сечения определяется требуемая
величина момента сопротивления для прокатных сечений
или характерных размеров для других сечений:

В случае, например, прямоугольного сечения
необходимо задать один из размеров или соотношение
между ними. Пусть h / b = k.
Тогда требуемая высота сечения:

формулы напряжений при изгибе следует, что наибольшие (положительные – растягивающие)

и наименьшие (отрицательные – сжимающие) напряжения в поперечном сечении зависят от величины осевого момента инерции или осевого момента сопротивления:


При изменении размеров сечения изменяются как осевой момент сопротивления, так площадь сечения. При этом величина осевого момента сопротивления зависит, например, для прямоугольного сечения, от квадрата высоты сечения, а площадь – линейно. Увеличение площади увеличивает расход материала на изготовление балки. Более рациональным сечением считается такое сечение, при котором отношение момента сопротивления к площади имеет большее значение. Для этого следует возможно большую часть площади поперечного сечения располагать как можно дальше от нейтральной оси. Ниже показаны 5 поперечных сечений балки, составленных из неравнобоких уголков и листа, площадь всех сечений одинакова, а моменты сопротивления различны:

В связи с тем, что площади этих сечений одинаковы,
наиболее рациональным из них является то,
у которого момент сопротивления Wx больше.

■ Добиться снижения веса балки можно также путем изменения размеров
сечения по ее длине в соответствии с изменением величины изгибающего
момента.
Поскольку эпюра изгибающего момента имеет в общем случае криволинейное
очертание, то для получения рационального сечения размеры, например высота
или толщина полок, должны непрерывно изменяться.
Из технологических соображений вместо этого используют ступенчатое
изменение толщины, достигаемое приваркой или приклепыванием
дополнительных горизонтальных листов:
На рисунке изображена, так называемая, эпюра материалов,
ординаты которой равны произведению момента сопротивления
поперечного сечения на допускаемое напряжение:

балки, кроме изгибающего момента, действует также поперечная сила.
При прямом поперечном

изгибе изгибающий момент действует в плоскости, совпадающей с одной из главных плоскостей инерции поперечного
сечения балки. Поперечная сила при этом обычно параллельна плоскости действия изгибающего момента.

Выделим малый элемент двумя нормальными к оси бруса и заменим действие отброшенных частей
нормальными напряжениями и касательными напряжениями. Под их действием элемент находится в
равновесии.

Поскольку закон изменения касательных напряжений по сечению неизвестен,
то из этого уравнения найти касательные напряжения для известной поперечной силы нельзя.

■ Касательные напряжения при поперечном изгибе - В общем случае при поперечном изгибе балок произвольного профиля могут
возникать две компоненты полного касательного напряжения в сечении. Компонента zx для такого сечения не может быть найдена методами
сопротивления материалов. Касательные напряжения zy, возникающие в поперечном сечении, связаны с поперечной силой, действующей
в этом сечении бруса, интегральной зависимостью:

z

z

zy

При действии поперечной силы изгибающий момент в сечении, отстоящем на расстоянии dz от другого
сечения, имеет приращение dMx.

Mx

Qy

Согласно зависимости нормальные напряжения также получают приращения:

z+dz

z

zy

Отсечем от рассматриваемого элемента некоторую ее часть горизонтальной плоскостью и заменим
ее действие касательными напряжениями (нормальные напряжения в соответствии с гипотезой об
отсутствии сдавливания продольных волокон не рассматриваются).

yz

zy

Оставшийся элемент по-прежнему находится в равновесии. Уравнение равновесия в проекции на ось z:

или

Здесь Aотс – площадь отсеченной части поперечного сечения, A1 – площадь горизонтального сечения элемента, равная bdz.

Aотс

A1

Перенесем первый интеграл в правую часть и подставим в него выражение для нормальных напряжений:

Приращение изгибающего момента и осевой момент инерции сечения не зависят от площади
отсеченной части и их можно вынести за знак интеграла. Оставшееся подинтегральное выражение совпадает с выражением для статического момента площади отсеченной части поперечного сечения:

Полагая касательные напряжения постоянными по площади A1, что соответствует предположению постоянства деформаций сдвига по ширине поперечного сечения, учитывая закон парности касательных перемещений и дифференциальную
зависимость поперечной силы, получаем:

или

Формула Журавского

Вывод формулы касательных напряжений при поперечном изгибе. Распределение касательных напряжений для некоторых типов поперечных сечений. Условие прочности на сдвиг. Понятие центра изгиба.

модулями упругости при растяжении и сдвиге. Кручение стержней круглого поперечного

сечения. Напряжения и перемещения. Анализ напряженного состояния.

Понятие о чистом сдвиге – Кроме деформации растяжения или сжатия материал нагруженного элемента конструкции может испытывать деформацию сдвига. Примером этому может служить напряженно-деформированное состояние элемента стенки балки в произвольном сечении, рассмотренное в предыдущей лекции. Там же было показано, что в опорных сечениях на нейтральной оси на гранях элемента отсутствуют нормальные напряжения, а касательные напряжения максимальны.
Другим примером, можно сказать классическим, является кручение тонкостенной трубы,
при котором любой элемент находится только под действием касательных напряжений.
Напряженно-деформированное состояние, характеризуемое тем, что на гранях
элемента возникают только касательные напряжения, называют чистым сдвигом.

22

Закон Гука сдвиге – Деформации чистого сдвига экспериментально изучаются
путем кручения трубчатых образцов. Экспериментальная диаграмма сдвига,
связывающая напряжения и угол сдвига, для пластичной стали имеет такой же характер
изменения, как и диаграмма растяжения:

y

yz

До напряжения пц , называемого пределом пропорциональности
при сдвиге справедлива линейная зависимость
(закон Гука при сдвиге):

Здесь  - относительный сдвиг:

G – модуль сдвига.

■ Связь между модулем сдвига и модулем упругости при растяжении – Модуль сдвига и модуль
упругости при растяжении являются физическими постоянными материала, характеризующими
жесткость в каждом из этих двух видов деформации. Поскольку удлинение диагонали элемента,
вызванное сдвигом, может быть получено также растяжением этого волокна под действием
нормальных напряжений, эти константы должны быть связаны между собой некоторым соотношением:

Касательное напряжение, при котором угол сдвига возрастает при постоянном напряжении называется
пределом текучести при сдвиге.

Таким образом существует соотношение между модулем сдвига и модулем упругости при
растяжении с участием коэффициента Пуассона. Любую из этих величин можно определить,
если известны две другие.

Удлинение диагонали элемента вследствие деформации сдвига (dy = dz):

ds

ds

Удлинение диагонали элемента вследствие деформации растяжения (σ1 =  , σ2 = - ):

или

характерно тем, что в поперечных сечениях возникают касательные напряжения ,

приводящиеся к крутящему моменту Mz.

z

x

y

Mz

Деформация стержня при кручении выражается тем, что поперечные сечения поворачиваются вокруг оси стержня
z на некоторые углы  = (z) , называемые углами закручивания.



z



Касательные напряжения при кручении – Как указывалось ранее, задача
определения напряжений является статически неопределимой, для решения которой
необходимо последовательно рассмотреть три стороны задачи:

1. Статика: Выделим малый элемент двумя нормальными к оси бруса сечениями
и заменим действие отброшенных частей касательными напряжениями.
Под их действием элемент находится в равновесии.

Ранее приведением распределенных сил к центру и центральным осям было
получено интегральное соотношение, связывающие крутящий момент
с касательными напряжениями:

dz

dz





Касательное напряжение произвольного направления в каждой точке
плоскости поперечного сечения можно разложить по двум другим
направлениям, а именно, по радиусу , соединяющему точку с центром
тяжести сечения, и по перпендикуляру к этому радиусу. Момент
относительно центральной оси z будет создавать лишь вторая компонента,
обозначаемая одним символом . Тогда:





Из этого соотношения найти напряжение по известному крутящему моменту пока нельзя, поскольку закон изменения напряжений по радиусу сечения неизвестен.

2. Геометрия: Согласно гипотезе плоских сечений при своем повороте сечения остаются плоскими (справедливо лишь для круглых сечений).
Следующее допущение состоит в том, что все радиусы сечения остаются прямыми и поворачиваются на один тот же угол (угол закручивания).

Mz

z

Mz

Угол закручивания двух смежных сечений отличается на величину dφ.

dφ

Угол сдвига в произвольной точке сечения, находящейся
на расстоянии  от центральной оси,
равен отношению длины дуги KK1 к dz:

K

K1





Длина дуги KK1:

3. Физика: По закону Гука при сдвиге:

Подставляем в интеграл:

Подставляем в выражение
для напряжений:

Полученная формула показывает, что касательные напряжения линейно зависят
от расстояния рассматриваемого волокна до центральной оси и принимают
Максимальные значения при  =max:

Условие
прочности
при кручении: [] – допускаемое касательное
напряжение материала стержня,
W - полярный момент
сопротивления:

закону парности касательных напряжений полученная формула для касательных напряжений, возникающих

в поперечном сечении, одновременно определяет касательные напряжения в плоскости, перпендикулярной продольному диаметральному сечению:

Каждый прямоугольный элемент материала испытывает напряженное состояние чистого сдвига.

Mz

Mz





Определение углов закручивания – При выводе формулы касательных напряжений
при кручении была получена дифференциальная зависимость:

Угол закручивания определяется из этого
дифференциального соотношения интегрированием
левой и правой части:
где 0 – угол поворота при z = 0.

z

В частном случае при постоянном моменте Mz, постоянной жесткости GIpи неподвижном сечении в начале координат (φ0 = 0) получаем:

Этой формулой можно пользоваться при определении угла для вала постоянного или
ступенчато постоянного сечения, нагруженного сосредоточенными моментами.
При этом на каждом из участков, на котором крутящий момент, жесткость постоянны, угол закручивания изменяется по линейному закону. Как следует из общей формулы определения угла закручивания, при построении эпюры углов закручивания ординаты эпюры откладываются от уровня предыдущего угла закручивания, т.е. строятся нарастающим итогом, учитывая угол закручивания предыдущего участка.

Пример: Построить эпюру углов закручивания для стержня нагруженного сосредоточенными моментами:
M1=5M, M2=4M, где M – параметр нагрузки, Ip2/Ip1 = 2.

1

2

1. Сечение I-I (0 < z1< l):

2. Сечение II-II (0 < z2< l):

Расчеты на жесткость – Валы машин испытывают переменные (динамические) нагрузки. При малой
жесткости валов могут возникать нежелательные крутильные колебания. Поэтому, помимо условий прочности
должны выполняться условия жесткости, ограничивающие величину максимального угла закручивания,
отнесенного к длине (погонного угла закручивания):

неопределимости, основная система, уравнения совместности деформаций

■ Количество таких

“лишних” связей (разность числа искомых неизвестных усилий и числа независимых уравнений равновесия) характеризует
степень статической неопределимости системы. Степень статической неопределимости плоской системы может быть установлена рассмотрением
степени кинематической подвижности: W = 3Д – С – 2Ш – 3Ж, где Д – число дисков (твердых дел), С – число стержней, Ш – число шарниров,
Ж – число жестких заделок. При W = 0 система статически определима, при W < 0 – статически неопределима, при W > 0 – геометрически изменяема.

■ Иногда при достаточном числе связей они стоят так, что они не могут препятствовать определенным перемещениям. Такие системы
являются геометрически изменяемыми, как и системы с недостаточным числом связей. В некоторых случаях связи не включаются в работу
при малых перемещениях (деформациях) системы. Такие системы являются мгновенно изменяемыми системами. Для них характерно возникновение
значительных (близких к бесконечности) усилий в связях в положениях, в которых возможно равновесие.
Примеры:

Таким образом, последние две системы не могут нести нагрузку, методы выявления таких систем
изучаются в курсе строительной механики. Статически неопределимые системы обладают повышенной жесткостью и несущей
способностью. Поэтому они широко используются в строительной практике.

■ Расчет статически неопределимых систем методом сил основывается на использовании основной статически определимой системы,
образованной из исходной статически неопределимой системой отбрасыванием лишних связей. Действие отброшенных связей заменяется силами,
называемыми лишними неизвестными. Таким образом в уравнения равновесия системы войдут эти дополнительные неизвестные усилия.
Для нахождения лишних неизвестных составляются уравнения совместности деформаций ( или просто уравнений деформаций), смысл которых
заключается в том, перемещения в основной системе от действия нагрузки и лишних неизвестных усилий по направлению каждой из лишних
неизвестных должны отсутствовать (обращаться в ноль):

где n – количество лишних неизвестных.

деформаций могут быть записаны более подробно с выделением слагаемых от
действия

неизвестных сил и нагрузки:

Слагаемые от действия неизвестных
удобно представить в виде произведения
перемещения от единичного усилия
на величину этого усилия:

Здесь бij – перемещение по направлению
i –ого неизвестного от действия единичной силы
по направлению j – ого неизвестного:

Подставляя эти соотношения
в уравнения деформаций получим
систему канонических уравнений
метода сил:

Перемещения бij и  iq при изгибе определяются формулами Мора:

В случае учета деформаций сжатия-растяжения, например, при наличии в системе стержней, работающих только на сжатие-растяжение, формулы для перемещений содержат соответствующие дополнительные слагаемые:

Решением системы канонических уравнений
находятся неизвестные X1,…Xn, после чего
могут быть найдены внутренние усилия, также
как это делается в статически определимых системах.

Поскольку эпюры внутренних усилий от
единичных воздействий и нагрузки, построенные
для определения перемещений, уже имеются, то
расчетные эпюры могут быть построены
непосредственно суммированием воздействий
от найденных неизвестных усилий и нагрузки.
Например, для расчетной эпюры
изгибающих моментов:

Пример 1.

1. Выбираем основную систему (отбрасываем среднюю
опору и заменяем ее действие неизвестным усилием X1.

X1

2. Строим эпюру изгибающих моментов от нагрузки
в основной системе:

3. Строим эпюру изгибающих моментов в основной
системе от действия единичного усилия X1 = 1.

4. Запишем каноническое уравнение метода сил и
вычислим коэффициенты:

5. Вычислим величину X1 :

6. Построим эпюру M1X1 и сложим ее с эпюрой Mq:

прямого стержня, когда в сечении возникает лишь один вид внутреннего

усилия, относятся к простым деформациям стержня: осевое растяжение-сжатие, чистый сдвиг, чистый (плоский) изгиб, чистое кручение. В реальных конструкциях стержни могут подвергаться более сложным видам сопротивления, представляющих собой сочетание нескольких простых деформаций, происходящих одновременно. Таким образом, возможно появление в поперечном сечении различных комбинаций ненулевых компонент из шести внутренних усилий: N, Qx, Qy, Mx, My, Mz. Такие комбинации, например, возникают в поперечных сечениях пространственного ломаного стержня (рычаги сложной конфигурации, коленчатые валы и т.п.) даже при нагрузке, лежащей в одной плоскости.

■ Построение эпюр внутренних сил в пространственном ломаном стержне – Для определения
опасных сечений в таком стержне необходимо построить эпюры компонент внутренних усилий: N, Qx, Qy,
Mx, My, Mz. При построении эпюр следует руководствоваться следующими правилами:
1. Как и ранее, стержень разбивается на участки, границами которых являются сечения, в которых
приложены сосредоточенные усилия (сила, момент-пара сил), начинается или заканчивается равномерно
распределенная нагрузка (в том числе и распределенный крутящий момент). Границами участка являются
также начало и конец ломаного стержня. Теперь дополнительно границей участка следует считать
перелом оси стержня.

2. Вместо глобальной системы координат, с учетом пространственного изменения положения оси стержня
при переходе от участка к участку, удобно использовать локальные системы координат для каждого
из прямолинейных участков с началом, совпадающим с центром тяжести рассматриваемого поперечного
сечения. Ось z направляется по оси прямолинейного участка бруса, положительные направления осей
x и y, в общем могут выбираться произвольно, но рекомендуется для горизонтальных участков ось y
направлять вверх, ось x – вправо от оси y при взгляде навстречу оси z (правая система координат). Для других
(вертикальных, наклонных) участков положительное направление оси y можно выбирать произвольно,
ось x – по тому же правилу.

I

II

III

IV

V

z

x

y

y

x

z

y

z

x

x

y

z

F3

z

x

y

O

R

Rx

Ry

Rz

M0

Mz

Mx

My

N

Qy

Qx

3. Правило знаков для внутренних усилий. Напомним, что внутренние усилия определяются методом
сечений, в результате которого в поперечном сечении появляются напряжения, заменяющие действие
отброшенной части бруса, которые и приводятся в общем случае к шести компонентам внутренних усилий
N, Qx, Qy, Mx, My, Mz.

Поскольку внутренние усилия, приложенные к каждой из частей бруса (оставленной или отброшенной) имеют
противоположные друг к другу направления (аксиома действия и противодействия), то при определении знака
каждого из усилий используются не знаки проекций на оси, которые будут различны для каждой из частей, а
характер деформаций, которые остаются одинаковыми для обоих частей. Поэтому принимается:
продольная сила N - положительна, если приложенная к сечению сила растягивает рассматриваемую часть;
изгибающие моменты Mx, My – положительные, если приложенные к сечению силы растягивают нижние волокна бруса;
крутящий момент Mz - положителен, если при взгляде навстречу внешней нормали к сечению поворачивает его по часовой стрелке;
поперечные силы Qx, Qy - положительны, если при взгляде навстречу к заданной другой (парной) координатной оси, перпендикулярной оси
стержня, поворачивают сечение по часовой стрелке:

F4

Теперь на рисунке слева все внутренние усилия показаны положительными.

Сложное сопротивление. Построение эпюр внутренних усилий в пространственном ломанном стержне.

– Такая комбинация внутренних усилий характерна тем, что в поперечном

сечении возникают нормальные напряжения, которые могут вычисляться по отдельности и складываться в соответствии с принципом независимости действия сил:

Во многих учебниках, например [1], можно увидеть знаки + перед слагаемыми, которые
записываются ценою изменения направления осей x, у на противоположные или изменения
правил для знаков изгибающих моментов (моменты считаются положительными, если они
вызывают растяжение волокон, находящихся в первом квадранте, т.е. при x > 0 и y > 0).
Иногда формулу напряжений при совместном действии продольной силы и моментов
записывают в виде:

x

y

Далее, сохраняя обычную ориентацию координатных осей, будем использовать новое правило для знаков изгибающих моментов (моменты считаются положительными, если они вызывают растяжение волокон, находящихся в первом квадранте).
Тогда формула для напряжений принимает вид:

+

-

-

+

Выражение показывает, что напряжения в точке линейно зависят
от координат x, y. Для определения максимальных напряжений,
необходимо найти точку, максимально удаленную от нулевой
(нейтральной оси).

Здесь x, y – координаты точки, в которой отыскивается напряжение;
правила знаков изгибающих моментов соответствуют ранее принятым
правилам для плоского изгиба.

+

+

Здесь x, y – расстояния точки от координатных осей, в которой
отыскивается напряжение; изгибающие моменты берутся по модулю;
знаки слагаемых присваиваются по характеру деформаций
(растяжение или сжатие) от каждого из моментов.

N

My

Mx

+

+

Уравнение нулевой линии – Для получения уравнения нулевой линии
достаточно приравнять напряжения нулю:
Нулевую линию можно построить с помощью отрезков,
отсекаемых этой прямой на координатных осях, которые
определяются поочередным заданием нулевых значений
каждой из координат:

Таким образом, максимальное напряжение возникает в точке в правом верхнем углу
рассматриваемого прямоугольного поперечного сечения, которая наиболее удалена
от нулевой линии:

σmax

Этот же результат для данного простого сечения можно получить
без нахождения положения нулевой линии, рассматривая знаки
слагаемых напряжений в угловых точках :

+

+

-

-

+

-

+

+

+

+

Одновременное действие продольной силы и изгибающих моментов. Определение нормальных напряжений и положения нулевой линии. Косой изгиб

испытаниях материалов статической нагрузкой на центральное растяжение (сжатие) достигается предельное

состояние, характеризуемое наступлением текучести, появлением значительных остаточных деформаций и/или трещин. Для пластичным материалов за предельную или опасную величину напряжений принимается предел текучести Т, для хрупких – предел прочности В.
При эксплуатации конструкций в общем случае по площадкам элементарного объема возникают нормальные и касательные напряжения, пропорциональные увеличению нагрузки. Значение каждого из напряжений зависят от ориентации рассматриваемых площадок.

Вариацией углов поворота площадок можно определить площадки, свободные от касательных напряжений, на которых возникают максимальные нормальные напряжения. Такие площадки и напряжения называются главными (способы их определения для плоского напряженного состояния были рассмотрены на лекции 9 первой части курса).
Именно главные напряжения и могут служить объективной характеристикой напряженного состояния в точке, поскольку они являются инвариантами – величинами, независящими от ориентации площадок. В итоге при оценке прочности материала вместо рассмотрения 9 компонент напряженного состояния, зависящих от ориентации элементарных площадок, можно рассматривать всего 3 (1> 2> 3).

При работе конструкции под нагрузкой некоторые точки находятся в условиях плоского или пространственного
напряженного состояния, для которых возможны самые различные соотношения между главными напряжениями. Для
определения предельного (опасного) состояния в точке (и тем самым всей конструкции), следовало бы сравнить эти
напряжения с предельными. Однако, практически это сделать невозможно, поскольку провести эксперименты,
подобные испытаниям на центральное растяжение-сжатие до разрушения, пришлось бы сделать для каждого из
возможных соотношений между главными напряжениями, не говоря уже о том, что реализовать эти соотношения при
испытаниях технически трудно.

Таким образом, необходимо иметь возможность сопоставить прочность материала при плоском и
пространственном напряженном состоянии с результатами испытаний при одноосном растяжении-сжатии.
Эта задача решается с помощью выдвижения гипотезы о каком-то одном критерии, определяющим условие
перехода материала в опасное состояние, составляющим основу соответствующей теории прочности.
С использованием того или иного критерия главные напряжения, возникающие в конструкции, удается связать с
предельными механическими характеристиками, получаемыми при одноосном испытании. В результате определяется
некоторое эквивалентное напряжение, характеризующее рассматриваемое напряженное состояние, которое можно
сравнивать с предельным или допускаемым напряжением при одноосном растяжении-сжатии.

■ Критерий разрушения путем отрыва (хрупкое разрушение) – Возможно частичное или полное разрушение тела. Различают разрушение
вязкое и хрупкое, которое могут проявляться как одновременно, так и последовательно. Хрупкое разрушение происходит в результате быстрого
распространения трещины после незначительной пластической деформации или без нее. В последнем случае разрушение называется идеально
хрупким. При хрупком разрушении скорость распространения трещины велика (0,2-0,5 скорости звука), а излом имеет кристаллический вид. При
квазихрупком разрушении наблюдается некоторая пластическая зона перед краем трещины. Хрупкие трещины могут возникать при средних
напряжениях, не превышающих предел текучести. Часто трещины медленно растут и процесс их роста может составлять до 90% времени
“жизни” детали. Поэтому имеет значение не столько факт возникновения трещины, сколько темп ее роста.

Общие понятия о теориях прочности. Критерий разрушения путем отрыва (хрупкое разрушение). Краткие сведения от первой и второй теориях прочности. Теория прочности Мора

в опасное состояние – достижение деформациями предельного (опасного) значения.
С

использованием этого критерия
условие прочности имеет вид:

Здесь при вычислении максимальной деформации участвуют все три главные
напряжения:

Следовательно, условие прочности,
выраженное через главные напряжения принимает вид:

Теория учитывает все три главные напряжения, но экспериментально подтверждается лишь для хрупких материалов при условии,
что все главные напряжения отрицательны.
Таким образом, I и II вторая теории могут применяться лишь для хрупких материалов. Заметим, что хрупкие материалы часто обладают различными механическими характеристиками при растяжении и сжатии, Поэтому в этих случаях необходимо использовать соответствующие расчетные (допускаемые) напряжения.

I теория прочности - Теория наибольших нормальных напряжений: гипотеза перехода материала в опасное состояние – достижение одного из главных напряжений предельного (опасного) значения.
С использованием этого критерия
условие прочности имеет вид: Первое условие используется при 1> 2> 3 > 0, второе – при 3 < 0, если |3| > |1|

- при

- при

Теория учитывает лишь одно из главных напряжений, экспериментально подтверждается лишь для хрупких материалов при условии,
что одно из главных напряжений значительно больше других.

Поля нормальных и касательных напряжений у вершины трещины описываются некоторыми функциями,
полученные методами теории упругости, в которые входит коэффициент интенсивности напряжений,
имеющий различные значения в зависимости от типа деформации трещин:
I – трещина нормального отрыва;
II – трещина плоского сдвига;
III – трещина антиплоского сдвига.
Ниже рассматриваемые три теории прочности основываются на критерии разрушения путем отрыва.

Теория прочности Мора – использует предположение, что напряжение 2 мало влияет на прочность материала (в пределах 15%). Таким образом расчет прочности в общем случае трехосного напряженного состояния сводится к расчету прочности при двухосном напряженном состоянии.
Это не означает, что в условии для II теории просто следует приравнять 2 нулю. Здесь расчетное напряжение определяется с учетом двух испытаний: на растяжение - р и на сжатие - с.

состояниях материала при нескольких различных соотношениях между
напряжениями 3 и 1.

Изображая каждое из состояний кругами Мора получим некоторое семейство таких кругов:
для двухосного напряженного состояния – круги черного цвета;
для одноосных растяжения и сжатия – круги красного цвета;
для чистого сдвига – круг синего цвета.

+

+

-

-

Одноосное
сжатие

Одноосное
растяжение

Чистый
сдвиг

Двухосное
напряженное
состояние
(сжатие)

Двухосное
напряженное
состояние
(растяжение)

Для материалов, сопротивление которых при сжатии больше, чем при растяжении, огибающая
предельных напряжений (пунктирная кривая) приближается к положительной оси абсцисс
и пересекает ее в точке A, соответствующей двухосевому равномерному растяжению.
Эксперименты показывают, что при всестороннем сжатии материал не разрушается при любых,
сколь угодно больших напряжениях. Поэтому огибающая не пересекает ось абсцисс при сжимающих
напряжениях.

A

Уменьшая круги предельных напряжений в n раз (n – коэффициент запаса) получим область,
соответствующую допускаемым (безопасным) напряженным состояниям:

р

с

Поскольку получить достаточно большое количество опытных данных затруднительно, обычно
ограничиваются лишь двумя испытаниями ( на растяжение и на сжатие) и огибающие кривые
заменяют прямыми, касательными к кругам Мора, построенным по этим испытаниям:

Для такой упрощенной диаграммы предельных напряженных состояний возможно получить
аналитическое условие прочности из подобия прямоугольных треугольников:

1

3

0.5с

0.5р

0.5с

0.5р

0.5с-0.5р

0.5(3-1)

0.5(3+1)

Сократим на 0.5 и перемножим:

После сокращения, сложения и сокращения
на 2 получим:

Отсюда соотношение, удовлетворяющее линии
предельных циклов:

Следовательно, условие
прочности имеет вид:

Теория Мора хорошо
согласуется
с экспериментальными
данными
при σ1> 0, σ3< 0.
Недостатком теории
Мора является неучет
промежуточного главного
напряжения σ2.

было обнаружено, что в пластическом состоянии максимальное касательное напряжение имеет

одно и то же значение для данного материала. В результате в качестве следующей гипотезы перехода материала в предельное состояние можно выбрать достижение наибольших касательных напряжений предельного (опасного) значения (критерий пластичности). Эта гипотеза легла в основу III теории прочности.
С использованием этого критерия
условие прочности имеет вид:

В случае плоского
напряженного состояния:

При изгибе с кручением:

Экспериментальные данные показывают хорошее совпадение результатов для пластичных материалов. Недостатком III теории по-прежнему
является неучет среднего главного напряжения 2 .

■ IV теория прочности (энергетическая) – Первоначальной попыткой связать все три главных напряжения было выдвижение гипотезы перехода в предельное состояние удельной потенциальной энергии деформации некоторого предельного значения. Эксперименты показали, что при всестороннем сжатии пластические деформации не возникают, хотя при этом накапливается большая удельная потенциальная энергия. В связи с этим была выдвинута гипотеза о том, что предельное состояние обуславливается достижением
предельного значения лишь той части удельной потенциальной энергии деформации, которая связана с изменением формы:

где

- полная удельная потенциальная энергия.

Удельную потенциальную энергию, затрачиваемую
на изменение объема, можно получить из этого
выражения, полагая 1 =2 = 3= о:

Подстановка обобщенного закона Гука
дает следующее выражение для полной удельной
потенциальной энергии:

Удельная потенциальная энергия, затрачиваемая на изменение формы:

Примем:

Критерий пластического состояния. Третья и четвертая теории прочности. Оценка прочности с применением теорий прочности. Понятия о новых теориях прочности и механики разрушения

и вычитания дает:
или
Для одноосного растяжения при наступлении текучести 1 =

Т , 2 = 3 = 0 удельная потенциальная энергия
составляет величину:

Замечание: Эти же соотношения можно получить непосредственно
из выражения для полной удельной энергии деформации

задавая по главным площадкам напряжения, равные разности действующих главных напряжений и среднего напряжения: 1’ = 1 - о, 2’ = 2 - о, 3’ = 3 - о:


и подставляя значение среднего напряжения:

Приравнивая выражения удельной потенциальной энергии изменения формы для трехосного напряженного состояния и для одноосного, получаем эквивалентное напряжение:

или

При изгибе с кручением:

Как и теория III, энергетическая теория показывает хорошее совпадение результатов
с экспериментальными данными для пластичных материалов.

■ Понятия о новых теориях прочности и механики разрушения – Предельная поверхность, соответствующая условию появления массовых
пластических деформаций по IV теории, определяется уравнением:
Уравнение соответствует поверхности
кругового цилиндра радиуса , ось которого равно наклонена к координатным осям 1,2 и 3.

Критерий, использованный в III теории дает поверхность правильной шестигранной призмы, вписанной в цилиндр, т.е. предельная область почти
совпадает с областью по IV теории. Критерий наибольших нормальных напряжений (I теория) дает куб с ребрами, равными о.
Новейшие теории прочности основываются на выборе различных вариантов предельной поверхности f(1,2, 3) = 0, при которой наиболее полно
можно учесть особенности сопротивления данного класса материалов в условиях сложного напряженного состояния. Например, в композитных
(армированных) материалах разрушение может частично происходить за счет разрыва волокон, а частично за счет скалывания матрицы.
В случае ортотропных материалов, имеющих различные пределы прочности, или материалов имеющие различные пределы прочности при сжатии
и растяжении условия прочности содержат константы, определяемые из соответствующих испытаний, т.е. используется не одно расчетное
сопротивление, а два и больше.

прочности и жесткости еще не гарантируют способности конструкции выполнять предназначенные

им функции. В определенных условиях отдельные элементы конструкции могут потерять устойчивую форму равновесия, после чего резко изменяется геометрия системы. В результате этого, как правило, изменяется характер нагружения и величина внутренних усилий, что приводит к невозможности дальнейшей эксплуатации конструкции или просто к катастрофическому обрушению.

Есть восстанавливающая
сила (сила тяжести
возвращает шарик
к положению равновесия).
Положение равновесия
устойчивое.

Восстанавливающей
силы нет
и нет силы, выводящей
шарик из положения
равновесия.
Положение равновесия
безразличное.

Восстанавливающая
сила есть (реакция
упругой связи – пружины
возвращает шарик
к положению равновесия).
Положение равновесия
устойчивое.

Есть восстанавливающая
сила (реакция пружины)
и сила, выводящая шарик
из положения равновесия
(сила тяжести).
Необходим анализ.

Нет восстанавливающей
силы (сила тяжести
уводит шарик
от положения равновесия).
Положение равновесия
неустойчивое.

В зависимости от того, как ведет себя система при малом смещении ее из положения равновесия различают
a) устойчивое равновесие, b) неустойчивое равновесие и c) безразличное равновесие:

Определение: Если при малых возмущениях тело отклоняется от своего невозмущенного (исходного) состояния равновесия незначительно,
то такое состояние равновесия называется устойчивым. Если же состояние равновесия не обладает таким свойством, то оно называется
неустойчивым.
Вполне очевидно из приведенных примеров, что при малых возмущениях (отклонениях от положения равновесия) устойчивая система (a, d)
стремится вернуться в исходное положение и совершает колебательное движение относительно своего положения равновесия.
Малость возмущений является важным условием данного определения устойчивости. При большом возмущении возможен переход в другое
положение равновесия, далекое от первоначального положения равновесия. В этом случае систему считают устойчивой “в малом” и неустойчивой
“в большом”.

a

b

c

d

e

В упруго деформирующихся системах силы упругости препятствуют уходу системы из начального положения равновесия. При малых возмущениях могут возникать силы, выводящие систему из этого положения. Анализ устойчивости заключается в оценке соотношений между этими силами. Например: Жесткий стержень AB длиной l , нагруженный продольной силой F, удерживается в равновесии упругой связью (пружиной) жесткости c.

F

В результате случайного воздействия (возмущения) стержень отклонился
от вертикального положения на малый угол б (sinб =б, бsB =lб):

б

бsB

Освободим объект от связей и составим моментное уравнение равновесия :

RB

XA

YA

Соотношение
упругости:

При б  0 возможно равновесие, если F = cl =
= F* (F* - критическая сила).

Понятие об устойчивых и неустойчивых формах равновесия. Формула Эйлера. Учет влияния способов закрепления концов стержня

из начального положения равновесия, при котором возможно другое (отклоненное) положение

равновесия, сколь угодно близкое к первому. При значении этой силы меньшем критического (F < F*), система имеет только одно – тривиальное – положение равновесия (б = 0). При значении этой силы равной критическому (F = F*), система имеет смежные положения равновесия, отклоненные от начального и мало отличающиеся от него(б  0). При значении этой силы большем критического (F > F*) система не может оставаться в начальном положении равновесия, а будет занимать какие-то другие положения в зависимости от значения силы. Эти положения можно найти решением соответствующего нелинейного уравнения (без предположения о малости перемещений).

F

б

бsB

XA

YA

MA

Замечание: Полученное значение критической силы в рассмотренном примере пропорционально жесткости упругой
связи (линейной пружины) и длины жесткой балки. Если рассмотреть пример, приведенный в [1], в котором возвращающее
усилие реализуется в виде пары сил (реактивного момента MA = cбφ) от спиральной пружины, то критическая сила получается
обратно пропорциональной длине стержня, т.е. при большей длине критическая сила меньше. Это говорит о том, что
геометрия системы, характер и место приложения реактивного возвращающего усилия влияет на величину критической
силы. Например, если линейная пружина будет поставлена на высоте a < l от шарнирно неподвижной опоры A,
то критическая сила соответственно уменьшается.

Формула Эйлера. При сжатии продольной силой деформируемого стержня его ось может получить малое искривление и в поперечных сечениях его возникнет упругий изгибающий момент, противодействующий дальнейшему искривлению стержня, численно равный моменту сжимающей силы относительно центральной оси поперечного сечения, смещенного на малое расстояние от прямолинейной оси стержня:

F

YA

ZA

Mx

RB

z

y

y

= 0

Запишем приближенное дифференциальное уравнение упругой линии, полученное
при выводе формулы для нормальных напряжений с использованием уравнений равновесия,
и подставим значение
изгибающего момента:

Приведем его
к стандартному виду:
Здесь

Решение полученного однородного
дифференциального уравнения известно
и имеет вид:

Постоянные интегрирования определяются из граничных условий:
z = 0, y(0) = 0;
z = l, y(l) = 0.

Это уравнение имеет два решения:
С2 = 0 – прогиб тождественно равен нулю по всей длине стержня (прямолинейная форма равновесия);
С2  0 – тогда sin kl = 0. Последнее определяет формы упругой линии n = 1, 2, 3,…..
(криволинейных форм равновесия):

При n = 1 получаем
наименьшее значение
силы:

Формула Эйлера

Таким образом, Fкр представляет собой наименьшую (критическую) сжимающую силу,
при которой наряду с прямолинейной формой равновесия становится возможной другая
(изгибная) форма равновесия.
При n =1 стержень изгибается по полуволне синусоиды. Константа C2 остается
неопределенной (в рамках сделанных предположений о малости прогибов).
При n = 2 изгибная форма представляет собой полную волну синусоиды, при которой
величина критической силы увеличивается в 4 (!) раза. Но для реализации такой формы
изгиба необходимо поставить дополнительные горизонтальные связи в середине длины
сжимаемого стержня.

шарнирного опирания стержня по концам. На практике встречаются и другие

способы закрепления:

F

Для каждого из таких случаев необходимо
задать соответствующие граничные условия,
после чего можно получить необходимые
значения критической силы.
На практике поступают иначе: определяют
некоторую условную длину шарнирно опертого
по концам стержня, для которого критическая
сила будет равна критической силе для
рассматриваемого стержня. Эта условная
длина является длиной полуволны синусоиды,
которая может построена так, чтобы граничные
условия для данного стержня были выполнены:

l0=l

l0=2l

l0=0.7l

l0=0.5l

l0=l

l0=2l

Критическая сила для каждого из этих стержней
может быть получена по обобщенной формуле:
где μ – коэффициент
приведения длины (l0 = μl).

При вычислении критической силы для стержней, имеющих различные моменты инерции Ix  Iy, а также различное
закрепление концов в плоскостях yOz и xOz, следует предварительно определить гибкость стержня относительно
каждой из главных осей:
где μx, μy– коэффициенты приведения длины,
ix, iy– радиусы инерции сечения
относительно осей x и y.

φA=0

φA=0

φA=0

φB=0

φA=0

φB=0

φB=0

С использованием гибкости критическая сила определяется выражением:
Наименьшая критическая сила вычисляется относительно оси,
для которой гибкость стержня оказывается наибольшей.

Формула Эйлера в функции от гибкости

предположении, что выполняется
линейная зависимость деформации от напряжений (закон Гука). Между

тем полученная зависимость критической силы
от гибкости является гиперболической, при которой уменьшение гибкости приводит к таким большим значениям
критической силы, что напряжения могут превысить предел пропорциональности σпц. Таким образом критические
напряжение не должны
превосходить предел
пропорциональности:

Например, для стали 45 σпц = 195 МПа, E = 2.06∙105
МПа. Подставляя в это неравенство эти данные
получим предельную гибкость, больше которой
нельзя пользоваться формулой Эйлера:

Таким образом, гиперболой Эйлера можно
пользоваться только при гибкости большей
предельной, равной для данной стали 102, (показано
на графике жирной синей кривой).

Для стержней малой гибкости (для сталей  < 40-60) разрушение стержня происходит вследствие разрушения самого материала (для сталей – пластическое течение при напряжении σ = σт = 300 МПа). Таким образом, критические напряжения для таких стержней ограничиваются уровнем этого предельного напряжения (показано на графике жирной синей линией).

Для стержней средней гибкости (для сталей 40-60 <  < 102 ) теоретическое исследование устойчивости вследствие необходимости учета нелинейности существенно усложняется. Для практических расчетов Ф.С. Ясинским была предложена эмпирическая линейная зависимость, полученная на основе обработки экспериментальных данных, в виде: где a и b – константы, зависящие от материала
(сталь: a = 310 Мпа, b = 1.14 МПа,
дерево: a = 29.3 МПа, b = 0.194 МПа).

Таким образом, критические напряжения для стержней средней гибкости ограничиваются наклонной прямой (показано на графике жирной синей
линией, соединяющей предыдущие участки). В целом безопасные напряжения с учетом потери устойчивости находятся внутри области,
очерченной синим на графике.

Формула Ясинского

Формула Эйлера

Поскольку величина критической силы зависит от максимальной гибкости в одной из плоскостей, а применяемые формулы (Эйлера или Ясинского)
- в зависимости от диапазона, в который попадает гибкость (средняя или большая гибкость), то порядок определения критической силы
следующий: 1. Определяются коэффициенты приведения длины и максимальная гибкость из двух гибкостей относительно осей x, y.
2. Определяется для данного материала предельная гибкость и сравнивается с максимальной.
3. Если максимальная гибкость больше предельной, то используется формула Эйлера, если меньше – формула Ясинского.
(Для стержней малой гибкости критическая сила не вычисляется).

Пределы применимости формулы Эйлера. Формула Ясинского. Порядок определения критической нагрузки. Практический метод расчета сжатых стержней по нормам

стержней условие прочности имеет вид:
Здесь N – нормальное

усилие в стержне, R – расчетное сопротивление материала, Aнт – площадь поперечного сечения (нетто).
С учетом ограничения напряжения, связанного с потерей устойчивости, должно выполняться неравенство:
Здесь Aбр – площадь поперечного сечения брутто (без учета местных ослаблений – отверстия, канавки и пр.

Условие обеспечения определенного
запаса по устойчивости стержня:

Представим правую часть неравенства как
некоторую долю расчетного сопротивления:

Здесь коэффициент φ <1 определяет степень снижения расчетного сопротивления и называется коэффициентом продольного изгиба или коэффициентом уменьшения расчетного сопротивления для сжатых стержней. Поскольку он связан с величиной критических напряжений, то он зависит от гибкости стержня.
Значения коэффициента установлены Строительными нормами и правилами (СНИП) и приводятся в виде таблицы в функции от гибкости для различных марок стали и других материалов (чугун, дерево). Справа приведен фрагмент таблицы коэффициентов φ:

где ny – нормативный или требуемый коэффициент запаса,
[y] – допускаемое напряжение при расчете на устойчивость.

Таким образом, условие обеспечения определенного запаса по устойчивости стержня можно записать в виде, аналогичном условию прочности:
или
Замечания: 1. Во втором виде записи условия коэффициент  уменьшает площадь поперечного сечения и иногда его называют коэффициентом снижения грузоподъемности.
2. Во всех случаях коэффициент  учитывает уровень критических напряжений (или гибкости) в соответствии с изложенными выше правилами использования формулы Эйлера (или Ясинского). Следовательно, здесь не нужно находить предельную гибкость.

Подбор сечения сжатых стержней. При подборе сечения оказывается, что одно условие содержит два неизвестных: площадь поперечного
сечения и значение коэффициента продольного изгиба, поскольку  = (), а гибкость зависит от размеров сечения (конкретно радиуса инерции).
Всюду в литературе, в том числе в [1], описана последовательность подбора сечения сжатых стержней методом последовательных приближений:
1. Задается значение  , например,  = 0.5.

2. Вычисляется т р е б у е м а я п л о щ а д ь: и назначаются размеры.

3. Определяется радиус инерции:

4. Вычисляется гибкость:

5. По получившейся гибкости из
таблицы определяется действительное значение д.

6. Сравнивается полученное д с заданным ранее  и выполняется шаг 1
с заданием нового значения , например, равным среднему (полусумме) из них.

и Симпсона.
Способы вычисления интеграла Мора – Интеграл Мора, в котором

подинтегральное выражение есть произведение двух функций, может быть вычислен различными методами в зависимости от вида этих функций. Заметим, одна из них, связанная с эпюрой внутренних усилий от единичного сосредоточенного воздействия, всегда линейная.
1. Непосредственное интегрирование – практически не имеет ограничений по использованию.
2. Способ Верещагина – удобен на тех участках, на которых легко можно определить центр тяжести одной из эпюр (обычно это относится к эпюре от грузового воздействия).
3. Формула Симпсона – применима в случае квадратичного закона изменения эпюры от грузового воздействия Формула трапеций – применяется в случае линейности обоих эпюр.
4. Формула трапеций – применяется в случае линейности обоих эпюр.

Первый способ не требует никаких особых пояснений. Рассмотрим его на примере:

q

F1=1

1

M2=1

2

Грузовая эпюра на втором участке
тождественно равна нулю, так
что достаточно знать законы
изменения изгибающих моментов
лишь на первом участке.

Здесь отрицательное значение прогиба означает, что действительное
направление перемещения противоположно заданному направлению
единичной силы.

Здесь положительное значение угла поворота означает, что действительное направление угла поворота совпадает с заданным направлением единичного момента.

Способ Верещагина:

Вычисление интеграла вида может быть представлено
как “перемножение” эпюр, если одна из эпюр линейная, что мы и
имеем для эпюр изгибающих моментов от действия сосредоточенных
усилий.

l

a

z



dz

статический момент площади
эпюры Mq относительно оси y’

y’

zC

C

yC

yC

центра тяжести не справедливы для
“не чистой” квадратной параболы, являющейся результатом
сложения

линейной эпюры (от действия сосредоточенных
сил на границе участка) и параболической (от действия
равномерно распределенной нагрузки на участке).
Если это так, то следует разбить эту эпюру на две или три
более простых эпюры:

Пример. Вычислим прогиб и угол поворота сечения на конце консоли для предыдущего примера
способом Верещагина:

Формула Симпсона: Можно доказать, что разбиением сложной параболической эпюры, как было показано
выше, результат “перемножения” такой эпюры с линейной эпюрой выражается формулой:

e

f

Воспользуемся формулой Симпсона
для предыдущего примера:

Формула трапеций: Формула Симпсона в частном случае при линейности обеих эпюр (перемножение трапеций)
выражается формулой:

нагрузок возникающие напряжения, превышающие определенный предел, вызывают образование и накопление

повреждений. Этот необратимый процесс приводит к образованию трещины. Концентрация напряжений на краю трещины способствует дальнейшему ее развитию. При достижении длины трещины критического значения скорость продвижения трещины резко возрастает и конструкция разрушается изломом, идентичному хрупкому разрушению, даже при пластичных материалах. Последнее обстоятельство (факт хрупкого разрушения пластичных материалов) дало повод к предположению, что под влиянием переменных напряжений материал со временем постепенно перерождается, как бы “устает”.
Процесс постепенного накопления повреждений в материале под действием переменных напряжений, приводящих к образованию трещины и разрушению, называется усталостью.
Свойство материала противостоять усталости называется выносливостью.

Механизм усталостного разрушения – Процесс усталостного разрушения связан со структурной неоднородностью материала ( вариация размеров, формы и расположения отдельных зерен металла, ориентации кристаллографических плоскостей, наличие различных включений, дефекты кристаллической решетки и т.п.). При переменных напряжениях, даже не превосходящих в среднем по некоторой области предела пропорциональности, возникает в отдельных точках с неблагоприятным сочетанием неоднородностей, пластическая деформация – деформация сдвига по некоторым плоскостям под действием касательных напряжений с образованием микротрещин, которые далее под действием нормальных напряжений развиваются и сливаются между собой с образованием макротрещин.

Поверхность усталостного излома состоит из двух заметно
отличающихся друг от друга зон: зона постепенного развития
трещины – имеет гладкую поверхность с полосками, отражающими периоды роста трещины, зона хрупкого излома
– имеет крупнозернистое строение.
На рис.1 -3 показаны усталостное разрушение различных деталей – вала со шпоночной канавкой (трещина начала расти из левого ее угла), рельса (трещина начала расти на глубине 10 мм), вагонной оси (трещина начала расти из подповерхностного слоя).

1

2

3

Циклы напряжений и их параметры – Усталостная прочность материалов
при переменных напряжениях зависит от вида напряженного состояния и от характера
изменения напряжений в времени.
Определим напряжения в произвольной точке K на поверхности вагонной оси,
вращающейся с некоторой постоянной угловой скоростью z:

x

K

σа - максимальные напряжения в точках 1 (-), 2 (+)

zt

1

2

Возникновение и накопление усталостных повреждений. Механизм усталостного разрушения. Циклы напряжений и их параметры. Экспериментальное определение предела выносливости. Симметричный цикл и кривая усталости

оси показывает периодическое изменение величины (и знака!) во времени
с периодом

T (через промежуток времени T напряжение принимает одно и то же значение). Часть
графика напряжений, соответствующая полному периоду их изменений называется циклом
напряжений. В данном примере цикл симметричный (max = a, min = - a).

При наличии какой-то постоянной составляющей напряжений, например, при дополнительном
осевом сжатии или растяжении или вал имеет дисбаланс (неуравновешенную массу), цикл
становится асимметричным (|max|  |min| ):

Среднее напряжение цикла m = (max + min )/2:

m

Амплитуда напряжений цикла a = max - m = m - min = (max - min )/2.

Если знаки напряжений max и min различны, то такой цикл называется знакопеременным.

Если знаки напряжений max и min постоянны, то такой цикл называется знакопостоянным.

Если одно из напряженийmax или min равно нулю, то такой цикл называется отнулевым или
пульсирующим.

m

m

Любой цикл напряжений полностью характеризуется этими двумя параметрами.
Однако, асимметричность цикла удобно оценить отношением,
называемым коэффициентом асимметрии цикла:

Циклы, имеющие одинаковое значения коэффициента асимметрии называются подобными.

Экспериментальное определение предела выносливости. На настоящем этапе развития
науки о прочности нет возможности создать теоретические методы расчета на выносливость. В
связи с этим теория усталостной прочности строится на основе экспериментальных данных.
В результате большого числа испытаний для различных сталей и видов циклов получают
кривые усталости. Ее ординаты представляют собой значения максимальных напряжений
при которых происходит разрушение детали, а абсцисса – число циклов (N), которое
выдержала деталь до разрушения.

Образцы испытываются на
специальных машинах в зависимости
от вида нагружения. При испытании на
изгиб образец 1 закрепляется в патроне
2 шпинделя, передающего вращение,
поперечная нагрузка передается
с помощью пары подшипников 3, связанных
с грузовой траверсой. Счетчик оборотов
фиксирует число циклов.

получения первой точки (1) задается амплитудное напряжение a = 0.65-
0.75в.

При таком достаточно большом напряжении образец разрушается сравнительно
быстро и результат наносится на график:

Для следующего идентичного образца амплитудное напряжение снижается, образец
до своего разрушения работает дольше и полученный результат (точка 2) наносится на
график:

Для следующего идентичного образца амплитудное напряжение вновь снижается и
все действия повторяются:

Т.к. число циклов растет очень быстро, используется логарифмическая шкала по оси
абсцисс. Вместе с этим растет время испытания каждого следующего образца. С этим
и связана в первую очередь трудоемкость испытаний на выносливость. В процессе
длительных испытаний было установлено, что образцы, неразрушившиеся при N = 107
циклах, не разрушаются и при большем числе циклов. Собственно на это указывает
горизонтальность последних участков кривой, построенной по полученным точкам.
Напряжение r , соответствующее таким участкам, является характеристикой
усталостной прочности и называется пределом выносливости материала.

r

Число циклов, равное для стали N = 107, называется
базовым числом. При достижении числа циклов этого
значения испытания прекращаются.
Между прочим, вагонное колесо совершает примерно
такое число оборотов (циклов) на пути в 3 раза большем,
чем расстояние от Москвы до Владивостока.

Самым неблагоприятным циклом с точки зрения обеспечения выносливости является
симметричный цикл. Именно для такого цикла и проводятся чаще всего испытания на
выносливость. Полученный предел выносливости для симметричного цикла
обозначается как -1 ( коэффициент асимметрии r = -1). Эксперименты показывают,
что для сталей соотношение между пределом выносливости и пределом прочности
составляет:

При отсутствии данных о пределе выносливости для конкретной марки стали и при
невозможности проведения испытаний на усталость можно пользоваться этим
соотношением.
Замечание: Для цветных металлов кривая усталости не имеет горизонтального
участка и для них принимается в качестве базового числа N = 108. Соотношение
между пределом выносливости и пределом прочности:

практических случаях детали конструкций и машин работают под действием циклических

нагрузок, характеризуемых асимметричным циклом, то встает необходимость построения кривых усталости для каждого из возможных коэффициентов асимметрии. Это требует испытания уже не десятка образцов, а нескольких десятков.
Соответственно увеличивается время и трудоемкость испытаний, не говоря у же о том, что необходимы специальные приспособления, регулирующие величину постоянной составляющей нагрузки. Для некоторых марок стали такие испытания были проведены и на их основании были построены диаграммы предельных амплитуд в осях a , m:

Заметим, что в таких координатах, подобные циклы, для которых коэффициент
асимметрии одинаков, располагаются на лучах, проведенных из центра 0 диаграммы:

m

a

Для получения каждой из точек этой диаграммы требуется провести испытания
на выносливость, т.е. построить кривую усталости, при каждом конкретном
соотношении a, m, соответствующем определенному коэффициенту асимметрии:



Поскольку построение таких диаграмм предельных амплитуд для широкого набора
марок стали и других материалов представляет собой чрезвычайно трудоемкую
задачу, то используют схематизированные (упрощенные) диаграммы, строящиеся
по результатам двух или трех испытаний, одно из которых статическое на прочность.
Заметим, что точка A диаграммы соответствует пределу выносливости для
симметричного цикла (r = -1), а точка B – пределу прочности для хрупких
материалов, определяемому из статических испытаний (r = 1):

A

B

-1

B

Схематизированная диаграмма предельных циклов для хрупких
материалов представляет собой треугольную область:

0

0

Для пластичных материалов (сталь) предельным напряжением при
статическом нагружении является предел текучести, так что
схематизированная диаграмма предельных циклов для этих материалов
представляет собой также треугольную область, но с вершиной в точке C:

C

Т

Видно, что для пластичных материалов упрощенная диаграмма, построенная по
двум точкам мало соответствует действительной диаграмме предельных циклов.
Поэтому получила широкое распространение диаграмма, построенная с использованием
испытаний на усталость при отнулевом (пульсирующем) цикле (r = 0, точка D, a = m = 0.50):

D

45o

Через точки A и D проводится прямая:

Для пластичных материалов необходимо отсечь зону, в которой напряжения превышают предел текучести a + m > T :

a = 0.50

m = 0.50

45o

Т

Получившийся четырехугольник представляет диаграмму предельных циклов по трем испытаниям для пластичных материалов:

Асимметричные циклы и диаграмма предельных амплитуд. Факторы, влияющие на усталостную прочность. Диаграмма предельных амплитуд детали. Коэффициент запаса детали

деталей машин показывают, что
прочность при переменных напряжениях (предел выносливости) в

значительной мере зависит от формы (наличия концентраторов напряжений) и
размеров детали, состояния ее поверхности и действия окружающей среды (условия эксплуатации). При испытаниях на выносливость
используются стандартные образцы цилиндрической формы, диаметром 7-10 мм, имеющие полированную поверхность. Все другие образцы,
выполненные из тех же материалов, но отличающиеся от стандартных перечисленными качествами, при испытаниях показывают как правило
более низкий предел выносливость.

Концентрация напряжений – местное повышение уровня напряжений в местах резкого изменения размеров сечения,
около отверстий, выкружек и канавок. Оно оценивается теоретическим коэффициентом концентрации, полученным
методами теории упругости для каждого из видов концентраторов:


При циклическом изменении нагрузки в области концентрации напряжений зарождается и развивается трещина,
которая в дальнейшем приводит к усталостному разрушению. Для каждого из видов концентраторов должны быть проведены
соответствующие испытание на выносливость. Практически, вместо этого, влияние концентрации напряжений учитывается
введением эффективного коэффициента концентрации, определяемым, как отношение предела
выносливости стандартного (“гладкого”) образца к пределу выносливости образца с концентратором:

Хотя коэффициент kЭ должен определяться для каждого значения коэффициента
асимметрии, обычно ограничиваются данными для симметричного цикла:

Эффективный коэффициент концентрации меньше теоретического, что объясняется влиянием
микропластических деформаций на величину напряжений в зоне развития усталостной трещины. Этот
эффект зависит от материала и в общем мало связан с видом концентратора. В связи с трудоемкостью
испытаний на усталостную прочность часто эффективный коэффициент концентрации вычисляется
при помощи выражения: где q – коэффициент чувствительности материала
к концентрации напряжений.

Коэффициент чувствительности материала q сильно зависит от предела прочности и при больших его значениях (высокопрочные стали) приближается к 1, поэтому применение высокопрочных материалов при переменных нагрузках не всегда целесообразно. На графиках изменения q даны для различных значений  теоретического коэффициента концентрации. Для конструкционных сталей q ≈ 0.6-0.8. Для чугуна и бетона q = 0 и, следовательно, эти материалы не чувствительны к концентрации напряжений. Это объясняется тем, что структура таких материалов крайне неоднородна и вызывает внутреннюю (на уровне структурных составляющих) концентрацию напряжений, превышающую ту, которая создается геометрическими концентраторами, связанными с резким изменением размеров сечения.

Масштабный фактор – С увеличением площади поперечного сечения при прочих равных условиях усталостная прочность образцов снижается. Причинами этого являются большая вероятность появления дефектов и перенапряженных зерен металла, ухудшение качества металла в связи с увеличением объема поковки, а также проявлением некоторых особенностей
технологии обработки. Фактор учитывается введением масштабного коэффициента (  < 1),
определяемого как отношение пределов выносливости детали и стандартного образца (d0):

прочность, связаны с тем, что состояние поверхности в результате обработки

и эксплуатации может быть различным по степени присутствия микроскопических надрезов (обработка резцом), каверн (коррозия), которые провоцируют зарождение и развитие трещин. Естественно, что при повышении качества обработки (чистоты поверхности) усталостная прочность повышается, а при работе деталей в агрессивной среде – снижается. Для повышения усталостной прочности применяют в том числе такие технологические способы упрочнения поверхности, как наклеп поверхностного слоя (обдувка дробью, ультразвук, закалка токами высокой частоты), термоциклирование (электроконтактные технологии), напыление. В целях защиты от коррозии применяют различные антикоррозионные покрытия (окраска). Фактор качества поверхности учитывается введением коэффициента  < 1, определяемого как отношение пределов выносливости рассматриваемого образца и полированного :
Если одновременно учитывается влияние коррозии, то определяется соответствующий коэффициент (к < 1) и перемножается
с коэффициентом качества поверхности.

Диаграмма предельных амплитуд детали – Эта диаграмма строится на основе диаграммы предельных циклов, полученной по результатам испытания стандартных образцов, с учетом снижения предела выносливости для рассматриваемой детали, обусловленного только что рассмотренными факторами.

A

B

-1

B

O

C

Т

D

45o

aD = 0.50

45o

Т

Уравнение прямой AD можно получить используя
уравнение прямой, проходящей через две точки:

Коэффициент запаса детали для рассматриваемого рабочего цикла можно определить как
отношение отрезков прямой подобных циклов: или и

M

N

Для точки M:

σa

σm

σaM

σmM

m D= 0.50

При относительно больших значениях σm точка M попадает на прямую EC,
ограничивающую максимальное напряжение цикла пределом текучести
(или прочности). Тогда коэффициент запаса по пределу текучести:

E

Опыт показывает, что перечисленные
факторы влияют только на величины предельных
амплитуд a. Тогда для учета этих факторов нужно
пропорционально уменьшить амплитудные напряжения:

Для кручения диаграмма предельных амплитуд
имеет такой же вид, и коэффициент запаса
определяется аналогичным выражением:

При изгибе с кручением
используют эмпирическую
формулу:

вы
воспользовались этим материалом для подготовки к экзаменам
по рассмотренным разделам сопротивления

материалов.

Успеха всем!