Слайд 2 Список литературы
Абламская Л.В., Бабешко
Л.О., Бывшев В.А., Дрогобыцкий И.Н. и др. Экономико-математическое моделирование, «Экзамен»,
М., 2004, 2006.
Лабскер Л.Г., Ященко Н.А. Теория игр в экономике (практикум с решениями задач), «Кнорус», М., 2012.
Интрилигатор М. Математические методы оптимизации и экономическая теория, «Айрис Пресс», М., 2002.
Содержание курса
Структура экономических задач.
Метод математического моделирования решения экономических задач.
Основные
понятия и аксиома теории игр.
Минимаксные стратегии игроков и решение игры с седловой точкой.
Пример игры без седловой точки, смешанные стратегии игроков и основная теорема теории игр.
Алгоритмы решения игры при отсутствии седловой точки.
Игры с природой (элементы теории статистических решений).
Слайд 4§1. Структура экономических задач
Исходные данные:
Искомые неизвестные:
3. Взаимосвязи величин (1) и (2).
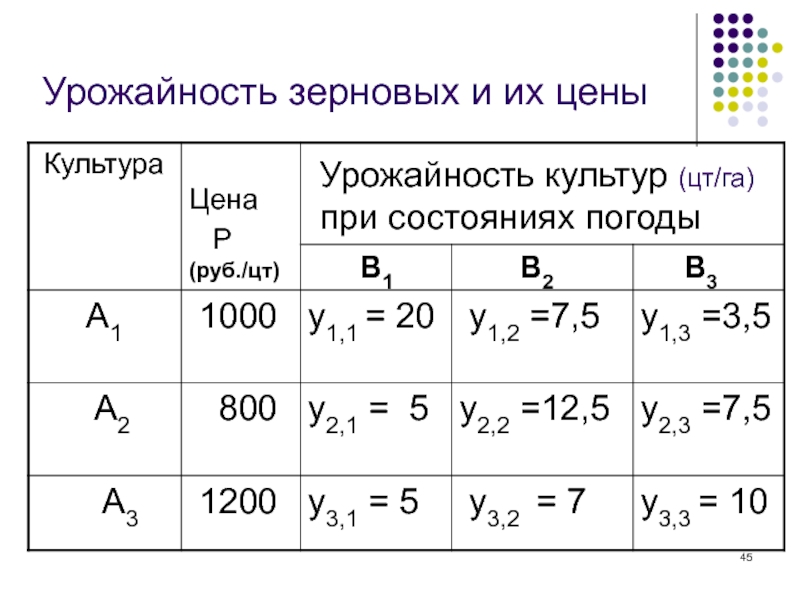
Слайд 5 Пример: задача об оптимальной посевной стратегии фермера
Фермер на своём участке земли может посеять
в текущем году одну из трёх культур: А1 - овёс, А2 - рожь, А3 – рис.
Урожайность каждой из этих культур зависит от погоды, которая может находится в одном из трёх состояний:
В1 - сухо, В2 - нормально, В3 – дождливо.
Уровни урожайности зерновых (yij) даны в следующей таблице вместе с их средними ценами.
Слайд 6Урожайность зерновых (цт/га) и их цены (руб./цт)
Урожайность культур при состояниях
погоды
Слайд 7Завершение формулировки задачи об оптимальной посевной стратегии фермера
Требуется:
выбрать оптимальную посевную стратегию фермера, предполагая, что о возможном состоянии
погоды отсутствует дополнительная информация.
Замечание. Посевная стратегия фермера считается оптимальной, если она приносит фермеру максимальный в определённом смысле доход.
Слайд 8Исходные данные и искомые неизвестные в задаче об оптимальной посевной
стратегии фермера
Исходные данные: 1) значения урожайности зерновых при различных
состояниях погоды:
2) Цены зерновых:
Искомые неизвестные: посевная стратегия Ai* , приносящая фермеру максимальный гарантированный доход
Слайд 9Взаимосвязи исходный данных и искомых неизвестных - значения дохода с
гектара для каждой посевной стратегии при возможных состояниях погоды:
Слайд 10§2. Метод математического моделирования в экономике
Метод математического моделирования (МММ)
решения экономических задач состоит в предварительном построении упрощённой схемы изучаемого
объекта (задачи или процесса),
составленной математическим языком и именуемой математической моделью, а затем - в вычислении по этой модели значений искомых величин (2):
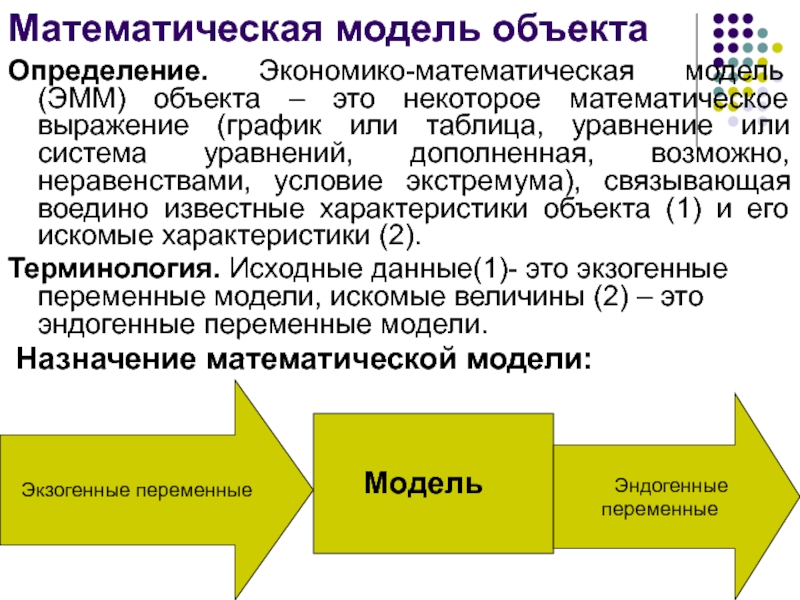
Слайд 11Математическая модель объекта
Определение. Экономико-математическая модель (ЭММ) объекта – это некоторое
математическое выражение (график или таблица, уравнение или система уравнений, дополненная,
возможно, неравенствами, условие экстремума), связывающая воедино известные характеристики объекта (1) и его искомые характеристики (2).
Терминология. Исходные данные(1)- это экзогенные переменные модели, искомые величины (2) – это эндогенные переменные модели.
Назначение математической модели:
Экзогенные переменные
Эндогенные переменные
Модель
Слайд 12Два класса ЭММ: дескриптивные модели и оптимизационные модели
Схема построения моделей обсуждается в книге: Бывшев В.А. Эконометрика,
2008.
Слайд 13Две формы ЭММ
Структурная форма:
дескриптивной модели –
(6),
оптимизационной модели – (7).
Приведённая форма (расчётная
схема) – (5).
Слайд 14§3. Основные понятия и аксиома теории игр
Участники конфликта (игроки) и
их стратегии
Ситуация игры и её исход
Слайд 15Пример конфликта (игры): ГНИ (игрок А) – Физическое лицо (игрок
В)
Y – налогооблагаемый доход игрока В за принятый отрезок времени.
Стратегии
игрока А:
А1 – проверять источники дохода В,
А2 - не проверять источники дохода В.
Стратегии игрока В:
В1 – утаивать доход Y,
В2 - не утаивать доход Y (платить налог Т).
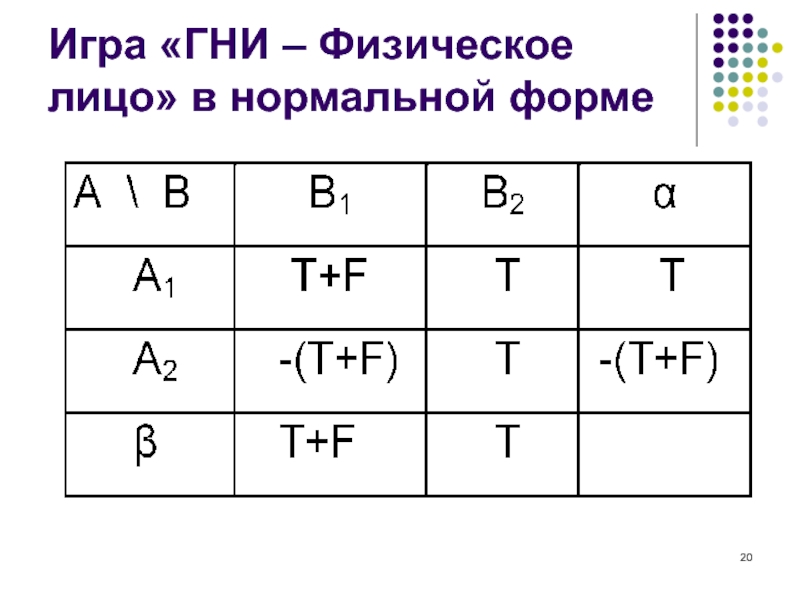
Слайд 16Продолжение примера игры «ГНИ – Физическое лицо»
Возможные ситуации игры:
(А1,В1), (А1,В2), (А2,В1), (А2,В2). (12)
Возможные
исходы игры:
R(А1,В1) = (T+F, - (T+F)),
R(А1,В2) = (T, - T), (13)
R (А2,В1) = (-(T+F), (T+F)),
R(А2,В2) = (T, - T).
Слайд 17Игра с нулевой суммой (антагонистическая игра)
Свойство игры с нулевой суммой:
Задание
исхода игры с нулевой суммой:
Платёжная матрица игры:
Слайд 18Пример. Платёжная матрица игры «ГНИ – Физическое лицо»
Слайд 20Игра «ГНИ – Физическое лицо» в нормальной форме
Слайд 21Аксиома (модель) поведения игроков
Ответ игрока А на выбранную игроком В
стратегию Bj:
Ответ игрока В на выбранную игроком А стратегию
Ai:
Слайд 22§4. Минимаксные стратегии игроков и решение игры с седловой точкой.
Порядок выбора оптимальной стратегии игрока А
Для каждой своей стратегии определить
гарантированный выигрыш αi:
Из величин (19) выбрать наибольшую (максимин),
и отметить соответствующую ей стратегию Аi(α).
Слайд 23Порядок выбора игроком B своей оптимальной стратегии
Для каждой своей стратегии
Вj определить
максимально возможный выигрыш βj игрока А:
Из
величин (21) выбрать наименьшую (минимакс):
и отметить соответствующую ей стратегию Вj(β).
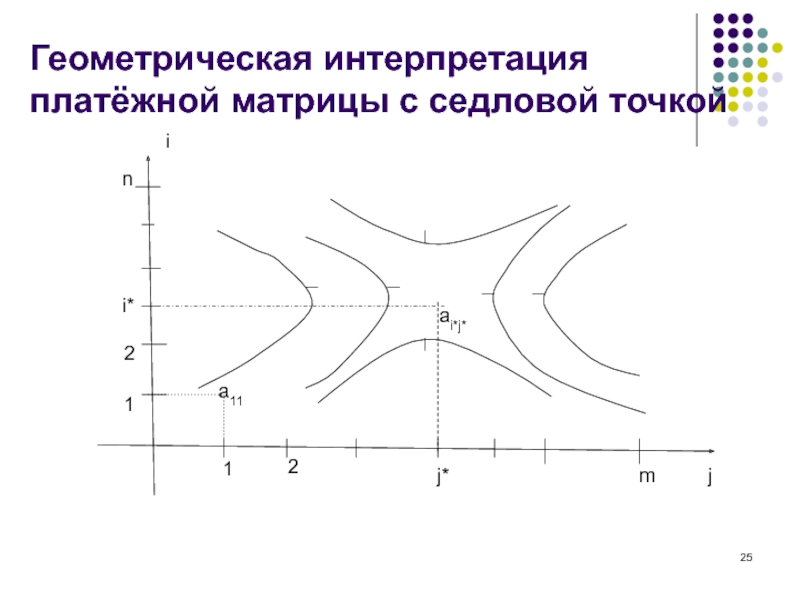
Слайд 24Оптимальные стратегии игроков в игре с седловой точкой
Теорема. Если
α = β, то игра имеет седловую точку и минимаксные
стратегии (Аi(α), Вj(β) ) являются оптимальными для игроков в следующем смысле:
Пример. Игра «ГНИ – Физическое лицо»:
Слайд 25Геометрическая интерпретация платёжной матрицы с седловой точкой
j
a11
ai*j*
1
2
j*
m
1
2
i*
n
i
Слайд 26 Терминология
Если игра
имеет седловую точку, то
величина v = α = β
именуется ценой игры,
набор называется решением игры,
стратегии Ai , Bj игроков именуются их чистыми стратегиями.
Замечание. В теоретико-игровой задаче исходными данными считается таблица с нормальной формой игры, а искомыми неизвестными – решение игры.
Слайд 27§5. Пример игры без седловой точки, смешанные стратегии игроков и
основная теорема теории игр
Пример (игра «загадай число»). Игроки
A и B ставят на кон по некоторому количеству денег M, затем записывают на своих листах выбранные ими по желанию натуральные числа (соответственно nA и nB) и, наконец, по команде открывают свои листы. Если сумма S = (nA + nB) оказывается чётным числом, то кон забирает игрок A, если же S нечётное число, то кон забирает игрок B.
Требуется определить оптимальные стратегии игроков в данной игре.
Слайд 28Стратегии игроков в игре «загадай число»
Стратегии игрока А:
А1 – выбрать чётное число nA,
А2 – выбрать нечётное число nA.
Стратегии игрока В:
В1 – выбрать чётное число nB,
В2 – выбрать нечётное число nB.
Слайд 29Запись игры «загадай число» в нормальной форме
Слайд 30Верхняя и нижняя цена игры «загадай число» в чистых стратегиях
и минимаксные стратегии игроков
Верхняя и нижняя цена игры:
α = -M; β = M.
Минимаксные стратегии игрока A: А1 и А2.
Минимаксные стратегии игрока B: B1 и B2.
Как в данной игре игроки должны выбирать свои стратегии?
Слайд 31Смешанные стратегии игроков
Определение. Смешанной стратегией игрока называется стратегия,
случайно выбираемая из множества его чистых стратегий, в соответствии с
заданными вероятностями такого выбора.
Смешанная стратегия игрока A:
Смешанная стратегия игрока B:
Слайд 32Средний выигрыш игрока A, верхняя и нижняя цена игры в
смешанных стратегиях
Средний выигрыш игрока A в смешанных стратегиях (выигрыш-функция игрока
А):
Нижняя цена игры в смешенных стратегиях (максимальный гарантированный средний выигрыш игрока А):
p q
Верхняя цена игры в смешанных стратегиях (минимальный гарантированный средний проигрыш игрока В):
q p
Слайд 33Пример: средний выигрыш игрока A в игре «загадай число» при
использовании игроками их смешанных стратегий
Платёжная матрица игры и смешанные
стратегии игроков:
Средний выигрыш игрока А в смешанных стратегиях:
Слайд 34Пример: расчёт нижней цены игры «Загадай число» в смешанных стратегиях
Расчёт
среднего гарантированного выигрыша игрока А:
q
Расчёт нижней цены игры в смешанных стратегиях (максимального гарантированного среднего выигрыша игрока А):
p p q
Слайд 35Пример: расчёт верхней цены игры «Загадай число» в смешанных стратегиях
Расчёт
максимального среднего проигрыша игрока В:
p
Расчёт верхней цены игры в смешанных стратегиях (минимального гарантированного среднего проигрыша игрока В):
q q p
Слайд 36Оптимальные стратегии игроков и цена игры без седловой точки
Теорема (основная
теорема теории игр (Дж. фон Нейман, 1928 г.). Для произвольной
игры с нулевой суммой, не имеющей седловой точки, существуют смешанные стратегии игроков , отклоняться от которых игрокам невыгодно в следующем смысле:
при этом
Слайд 37 Терминология и замечание
Если в
игре без седловой точки имеет место равенство α’ = β’,
то
величина v’ = α’ = β’ именуется ценой игры в смешанных стратегиях ,
набор называется решением игры в смешанных стратегиях,
стратегии игроков именуются их оптимальными смешанными стратегиями.
Замечание. Использование игроками смешанных стратегий предполагает многократное повторение игры.
Слайд 38§6. Алгоритмы решения игры при отсутствии седловой точки
Аналитическое решения игры
2 x 2
Слайд 39 Вычисление решения игры при помощи задачи линейного программирования
Если в
платёжной матрице С есть нулевые или отрицательные элементы, то ко
всем элементам ai,j платёжной матрицы прибавить величину
Решить задачу линейного программирования
Слайд 41 Продолжение алгоритма
Решить задачу линейного программирования
Слайд 43§ 7. Игры с природой (элементы теории статистических решений)
Определение. Игра
именуется «Игрой с природой», если один из игроков (игрок В)
на любую стратегию другого игрока (игрока А) отвечает некоторой фиксированной смешанной стратегией B’q, выбор которой не подчинён аксиоме оптимальности поведения игрока В в игре.
Замечание. В игре с природой игрок В именуется «природой». Стратегии игрока В именуются состояниями природы.
Слайд 44 Пример игры с природой (задача об оптимальной посевной стратегии
фермера)
Фермер (игрок А) на своём участке земли
может посеять в текущем году одну из трёх культур: А1 - овёс, А2 - рожь, А3 – рис.
Урожайность каждой из этих культур зависит от погоды (игрок В – природа), которая может находится в одном из трёх состояний:
В1 - сухо, В2 - нормально, В3 – дождливо.
Средние цены зерновых и их уровни урожайности (yij) при каждом состоянии погоды известны и даны в следующей таблице.
Слайд 45Урожайность зерновых и их цены
Урожайность культур (цт/га) при состояниях
погоды
Слайд 46Платёжная матрица (доходы фермера с гектара
)
Слайд 47Завершение формулировки задачи об оптимальной посевной стратегии фермера
Требуется:
выбрать оптимальную посевную стратегию фермера, предполагая, что
1) о возможных состояниях погоды отсутствует дополнительная информация,
2) известна дополнительная информация о состояниях погоды в виде их статистических вероятностей (q1, q2, q3).
Замечание. Посевная стратегия фермера считается оптимальной, если она приносит фермеру наибольший в определённом смысле доход.
Слайд 48Выбор стратегии в игре с природой по критерию Вальда
Максиминныйный критерий
Вальда. Игрок А должен выбирать свою максиминную стратегию Ai(α), приносящую
ему максимальный гарантированный выигрыш:
i j
Пример (задача о посевной стратегии фермера):
i j
Слайд 49Уровни риска стратегий игрока в игре с природой
Определение. Уровнем
риска стратегии Аi игрока А в ситуации (Ai,Bj) игры с
природой называется величина
Определение. Риском игрока А при выборе им стратегии Ai называется величина
j
Слайд 50Выбор стратегии в игре с природой по критерию Сэвиджа
Критерий минимального
риска Сэвиджа. Игрок А должен выбирать свою стратегию Ai(r), приносящую
ему минимальный уровень риска:
i j
Алгоритм выбора стратегии по критерию Сэвиджа
1) Определить при каждом состоянии природы максимальные выигрыши игрока А: β1, β2,…,βm.
Слайд 51Продолжение алгоритма выбора стратегии по критерию Сэвиджа
Составить согласно (36) матрицу
рисков R=(rij) и вычислить по правилу (37) уровни рисков всех
стратегий игрока.
Выбрать наименее рискованную стратегию Ai(r).
Пример. Выбор посевной стратегии фермера по критерию Сэвиджа.
Определяем при каждом состоянии природы максимальные доходы фермера: β1=20000, β2=10000,β3=12000.
Слайд 52Пример выбора стратегии по критерию Сэвиджа
Вычисляем матрицу рисков:
Вычисляем риски посевных
стратегий фермера:
r1= 8500, r2 = 16000,
r3=14000.
Выбираем наименее рискованную стратегию:
Слайд 53Выбор стратегии в игре с природой при известных вероятностях её
состояний
По известной платёжной матрице игры и известном смешанном состоянии природы
рассчитать для всех чистых стратегий Ai игрока А средние выигрыши:
Выбрать стратегию, обеспечивающую игроку А максимальный средний (ожидаемый) выигрыш:
Слайд 54 Обсуждённые вопросы
Структура экономических задач.
Метод
математического моделирования решения экономических задач.
Основные понятия теории игр и модель
поведения игроков.
Минимаксные стратегии игроков и решение игры с седловой точкой.
Пример игры без седловой точки, смешанные стратегии игроков и основная теорема теории игр.
Алгоритмы решения игры при отсутствии седловой точки.
Игры с природой (элементы теории статистических решений).