Курс линейной алгебры

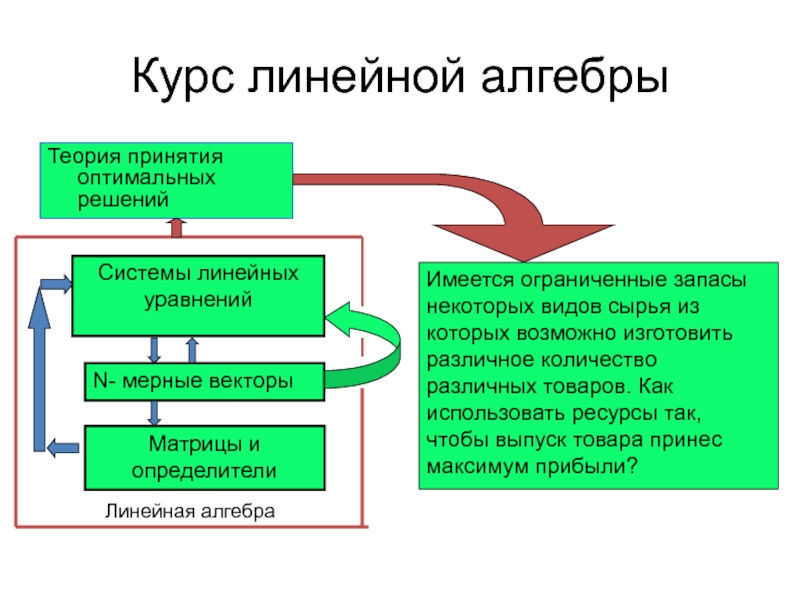
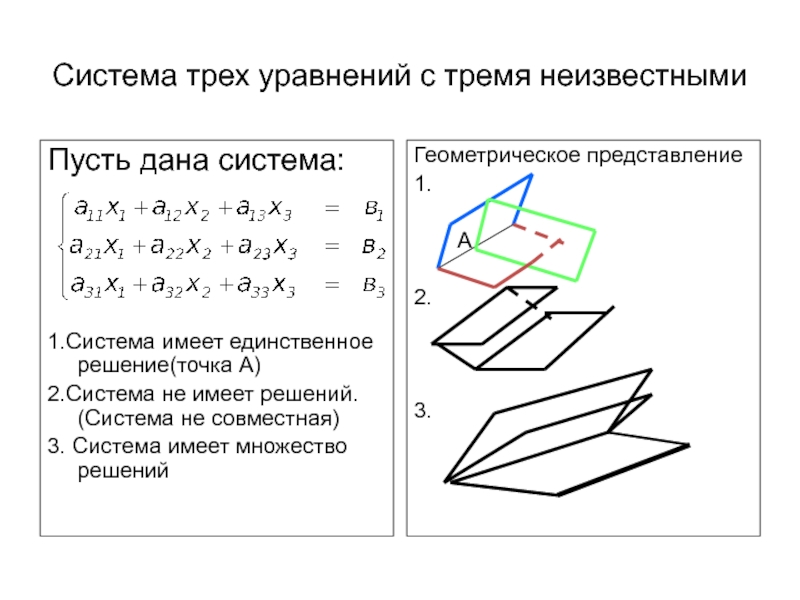
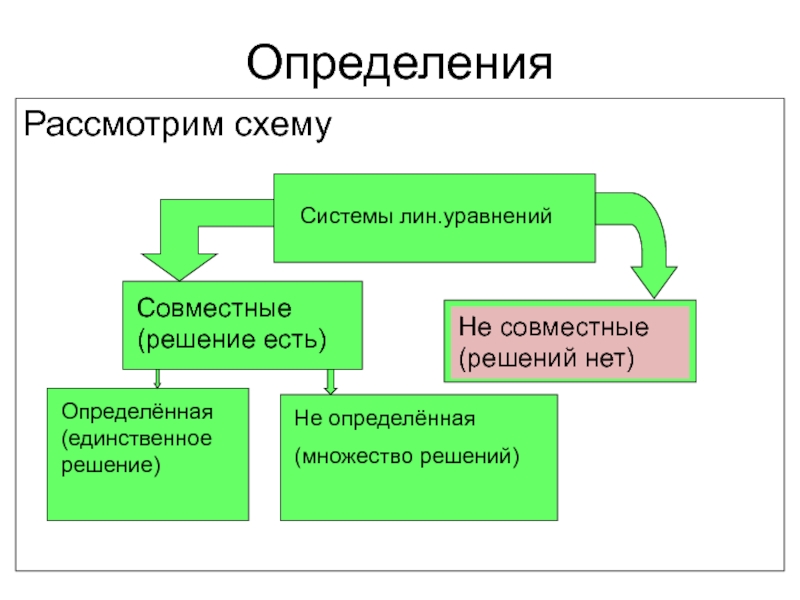
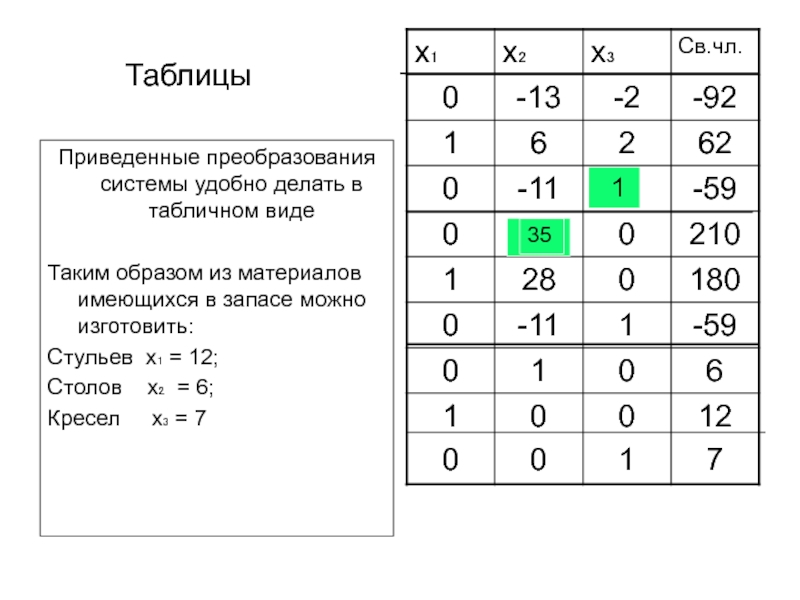
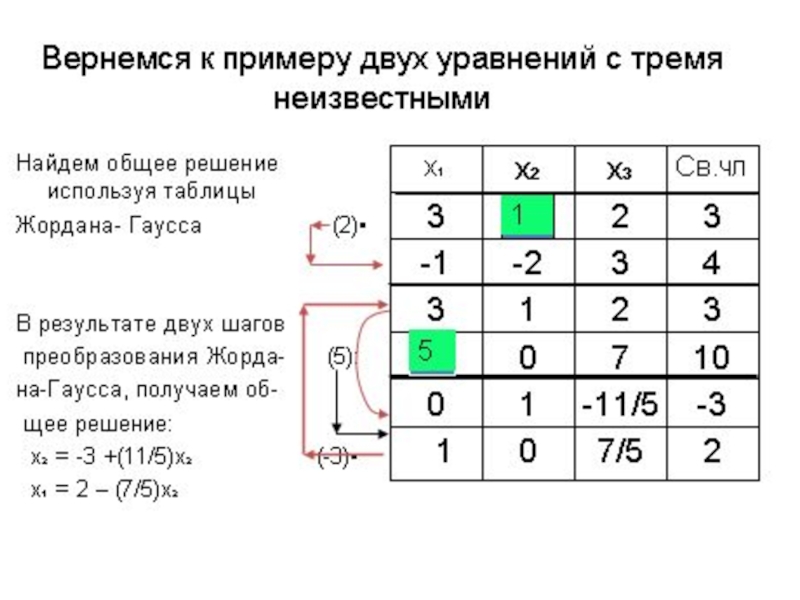
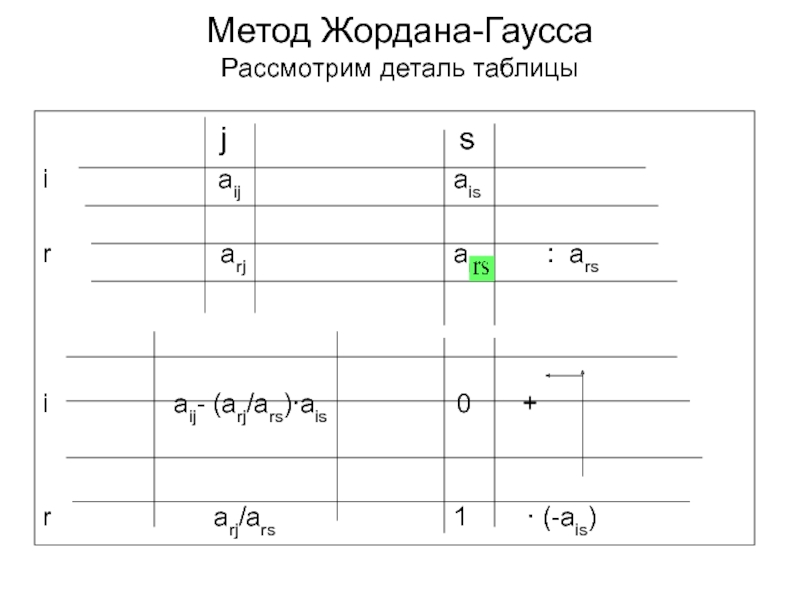
определители
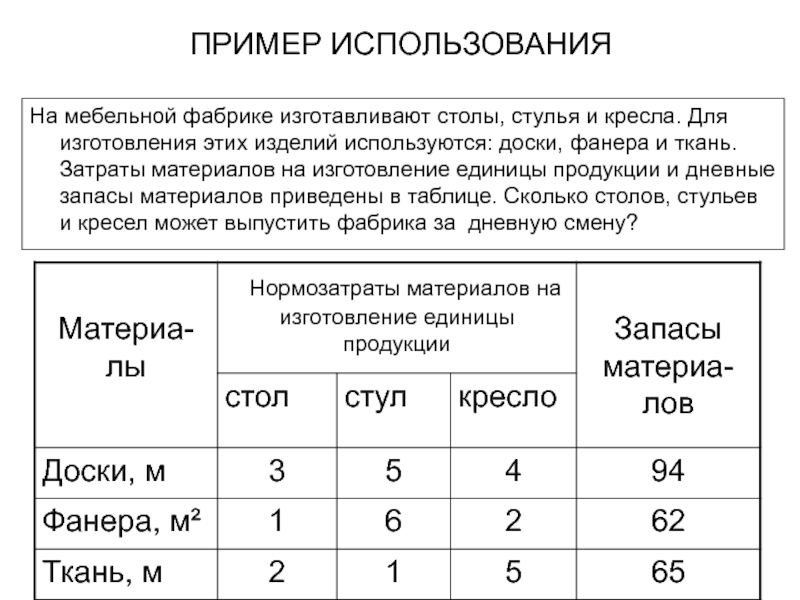
Имеется ограниченные запасы некоторых видов сырья из которых возможно изготовить

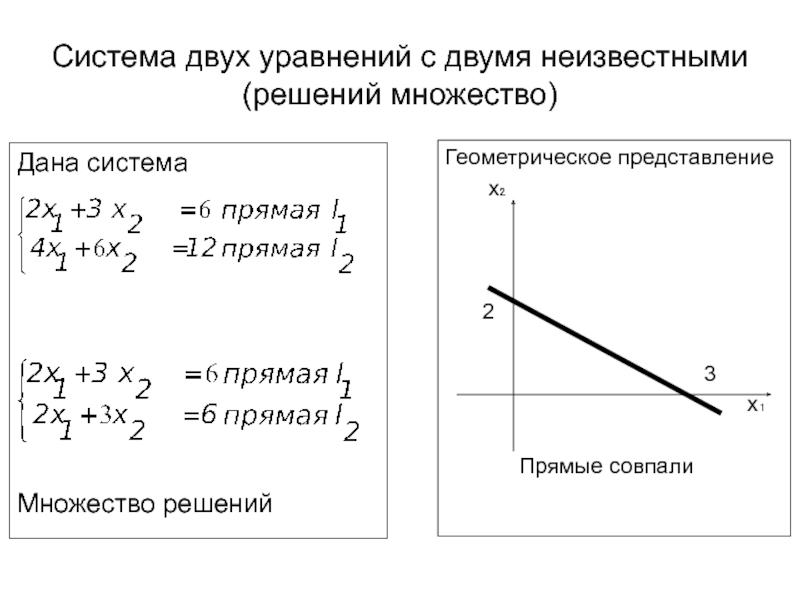
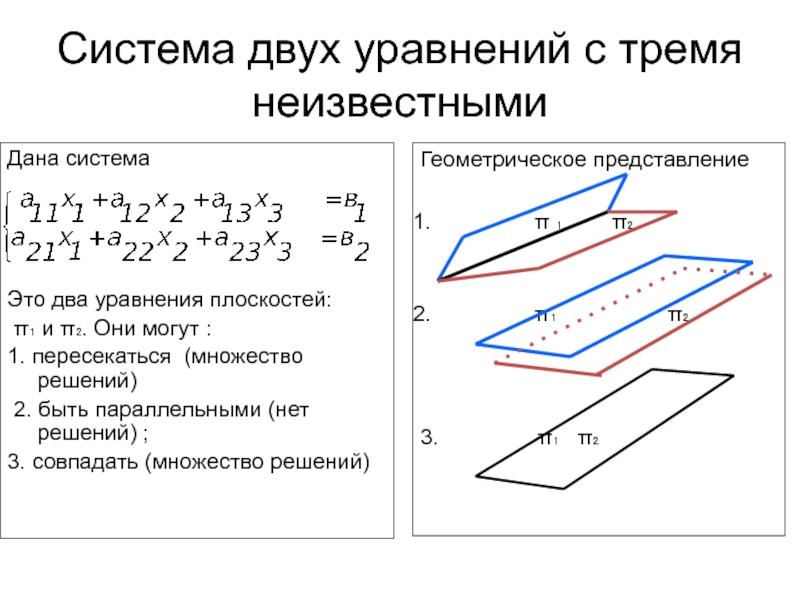
различное количество различных товаров. Как использовать ресурсы так, чтобы выпуск товара принес максимум прибыли?

Системы линейных уравнений

Линейная алгебра

проф. Сагитов Р.В.

изготовления этих изделий используются: доски, фанера и ткань. Затраты материалов

на изготовление единицы продукции и дневные запасы материалов приведены в таблице. Сколько столов, стульев и кресел может выпустить фабрика за дневную смену?

х₂

прямая l₁

х₀₂
х₀₁ прямая l₂ х₁

Решение системы – это пара чисел Х₀ = (Х₀₁; Х₀₂) при подстановке которых в систему уравнений, каждое уравнение превращается в правильное равенство

уравнений будет пара чисел Х=(3;-2)


Графическое представление

х₂
5/2
1
3 х₁
1 5/3
-2

решений не имеет. Система не совместная.




Графическое представление
х₂

2

1,5
2,25 3
х₁

представление
х₂



2

3
х₁

Прямые совпали

π₁ и π₂. Они могут :
1. пересекаться (множество решений)

2. быть параллельными (нет решений) ;
3. совпадать (множество решений)

Геометрическое представление

π ₁ π₂


π₁ π₂



3. π₁ π₂

Общим решением этой
системы будет набор

чисел: Х = (2 - 7/5∙х₃; -3 -11/5∙х₃; x₃), если свободной переменной x₃ придать частное значение, например х₃ = 0, то получим набор чисел, который называется частным решением Х =(2;3;0) . Придавая свободной переменной х₃ различные значения будем получать множество решений, соответствующих различным точкам лежащим на прямой пресечения плоскостей

решение(точка А)
2.Система не имеет решений. (Система не совместная)
3. Система имеет

множество решений

Геометрическое представление
1.

А

2.



3.

(решений нет)
Определённая (единственное решение)
Не определенная (множество решний)
Не определённая
(множество решений)

количество стульев, столов и кресел соответственно, которое возможно изготовить из

имеющихся запасов материалов, тогда математическая модель примет вид

в табличном виде

Таким образом из материалов имеющихся в запасе можно

изготовить:
Стульев х₁ = 12;
Столов х₂ = 6;
Кресел х₃ = 7

1

35

системы является набор чисел Х =(х1;х2;…хn) при подстановке которого в

систему каждое уравнение превращается в правильное равенство

Уравнение вида
0∙х1+ 0∙х2+… 0∙хn = 0 называется тривиальным

Уравнение вида
0∙х1+ 0∙х2+… 0∙хn = в называется противоречивым

Если система содержит противоречивое уравнение, то она не совместная

разрешенными
Переменные хm+1; хm+2 ; … хn называются свободными

являются решением другой и наоборот
Равносильные преобразования систем:
Вычеркивание тривиального уравнения;
Умножение любого

уравнения системы на число, не равное нулю;
Замена любого уравнения системы суммой с другим уравнением системы, умноженным на число, не равное нулю.

Равносильные системы линейных уравнений

Гаусс Иоганн Карл Фридрих
Мари Эдмон (1837-1922) (1777 – 1855) немецкий
Французский математик математик

j

s
i aij ais

r arj ars : ars



i aij- (arj/ars)∙ais 0 +


r arj/ars 1 ∙ (-ais)

j

s
i 3 7

r 5 8 : 8



i 3+(5/8)∙(-7) 0 +

r 5/8 1 ∙ (-7)

элементы аij‘ вычисляются по формулам

= 2
х1 – х2 + 2х3 – х4

= 2
4х1 + х2 + 3х3 - х4 = 6

всегда есть набор чисел Х = ( 0,0,…,0), который является

решением. Если m < n, то такие системы имеют ненулевые решения. Ниже будет показано, как найти эти решения.