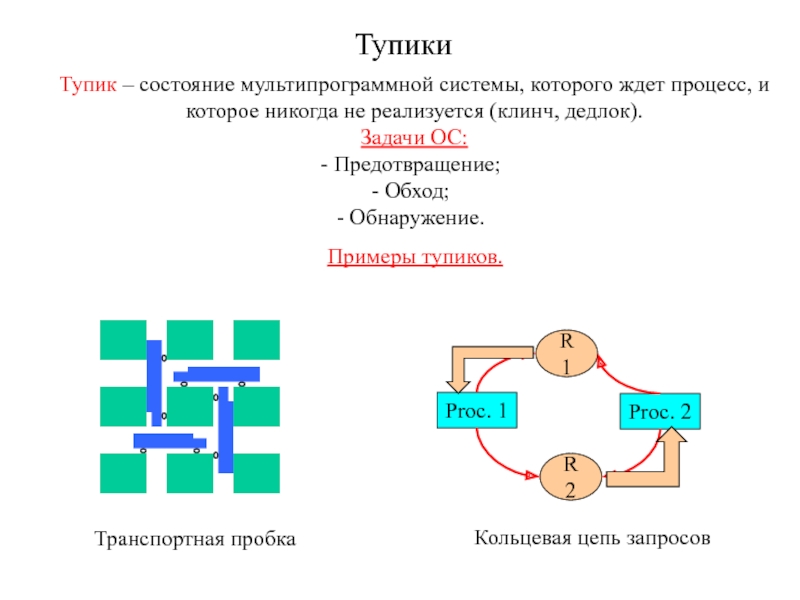
Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Курсовая работа по дисциплине: Теория электрической связи РАСЧЕТ ПРОЦЕССОВ
Содержание
- 1. Курсовая работа по дисциплине: Теория электрической связи РАСЧЕТ ПРОЦЕССОВ
- 2. Цель курсовой работы состоит в приобретении и
- 3. Цели заданий:В первых трех заданиях курсовой работы
- 4. Цели заданий:В заданиях № 7-9 ознакомиться и
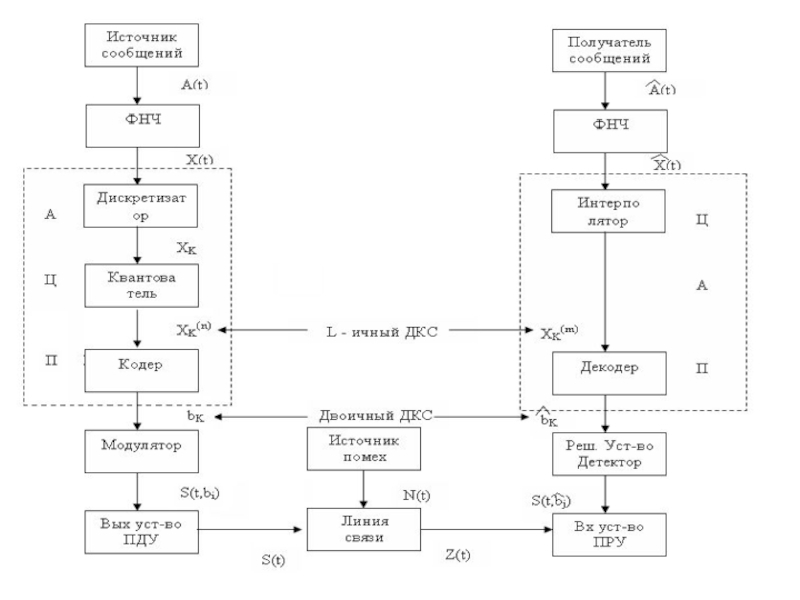
- 5. Задание 1Изобразить структурную схему электросвязи.Пояснить значения ее отдельных элементов.
- 6. Слайд 6
- 7. Источник сообщений – некоторый объект или система,
- 8. Квантователь – осуществляет квантование по уровню дискретизированных
- 9. Модулятор – устройство, предназначенное для согласования источника
- 10. Линия связи - совокупность физических цепей, имеющих
- 11. ПРУ – принимающее устройство или приемник, предназначенное
- 12. Декодер – устройство, восстанавливающее знаки сообщения из
- 13. Получатель сообщения – некоторый объект или система, принимающая информацию о состоянии или поведении источника сообщения.
- 14. Задание 2По заданной функции корреляции исходного сообщения:Рассчитать
- 15. Интервал корреляции – промежуток времени между сечениями
- 16. Расчетные формулы:
- 17. Пример Исходные данные:Мощность(дисперсия) сообщения Ра=2,2 ( В2)Коэффициент затухания
- 18. Вычислим интервал корреляции по формулеВычислим спектр плотности мощности получимпредварительно задав
- 19. Чтобы определить начальную энергетическую ширину спектра сообщения
- 20. Слайд 20
- 21. Как видно из графика Gmax=Ga(0) = 2.839∙10-4Вычислим
- 22. Слайд 22
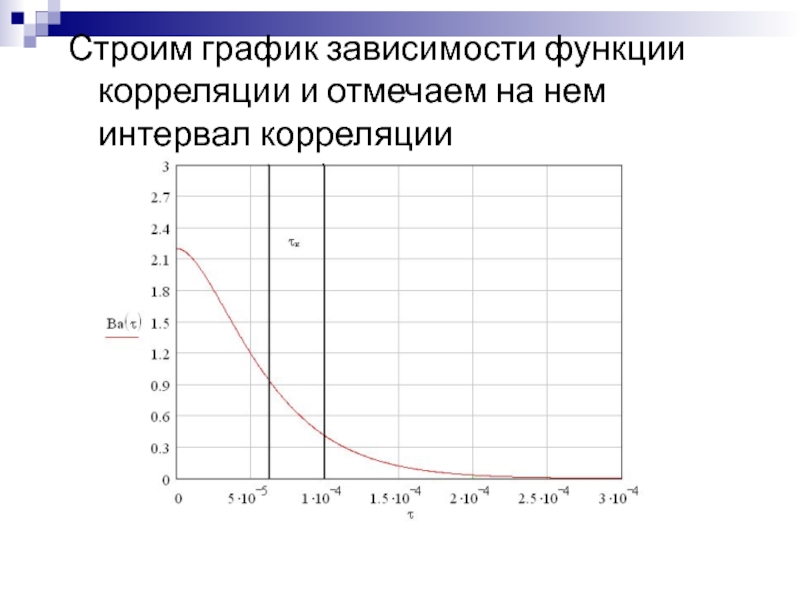
- 23. Строим график зависимости функции корреляции и отмечаем на нем интервал корреляции
- 24. Задание 3Считая, что исходное сообщение воздействует на
- 25. Расчетные формулы:Средняя мощность отклика ИФНЧ:Средняя квадратическая погрешность фильтрации (СКПФ):
- 26. По предложенным формулам вычислим среднюю мощность отклика
- 27. Получаем, что верхняя частота спектра:Fв = 3875
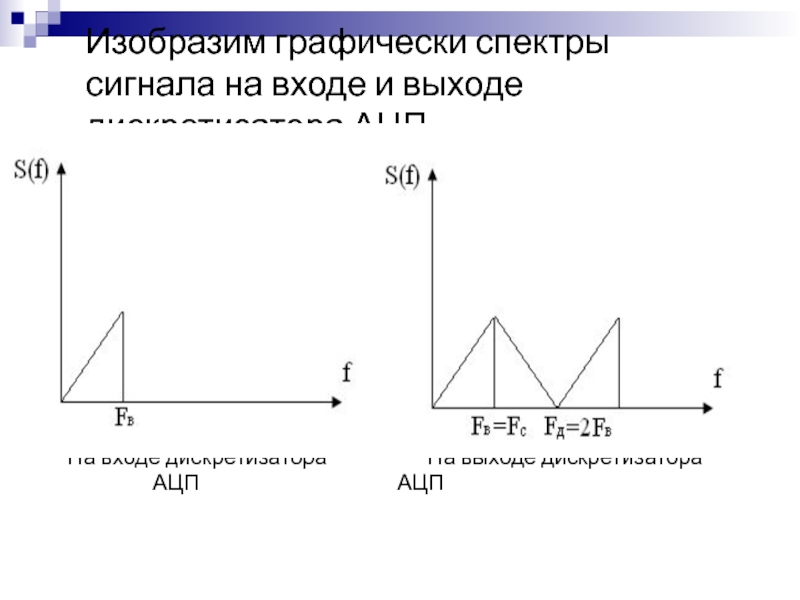
- 28. Изобразим графически спектры сигнала на входе и выходе дискретизатора АЦПНа входе дискретизатора На выходе дискретизатора АЦП АЦП
- 29. Задание 4Полагая, что последовательность дискретных отсчетов на
- 30. Расчетные формулы:Шаг квантования:Пороги квантования:Уровни квантования:
- 31. Средняя квадратическая погрешность квантования. где PХ
- 32. Коэффициент взаимной корреляции между входным и выходным
- 33. ПримерНапомним, что число уровней квантования L=16.Определим шаг
- 34. Рассчитаем среднюю квадратическую погрешность квантования (СКПК).
- 35. Распределение вероятностей дискретной случайной величины: Найдем интегральное распределение вероятностей:
- 36. Теперь найдем мощность крантованного процесс: Средняя квадратическая погрешность квантования:
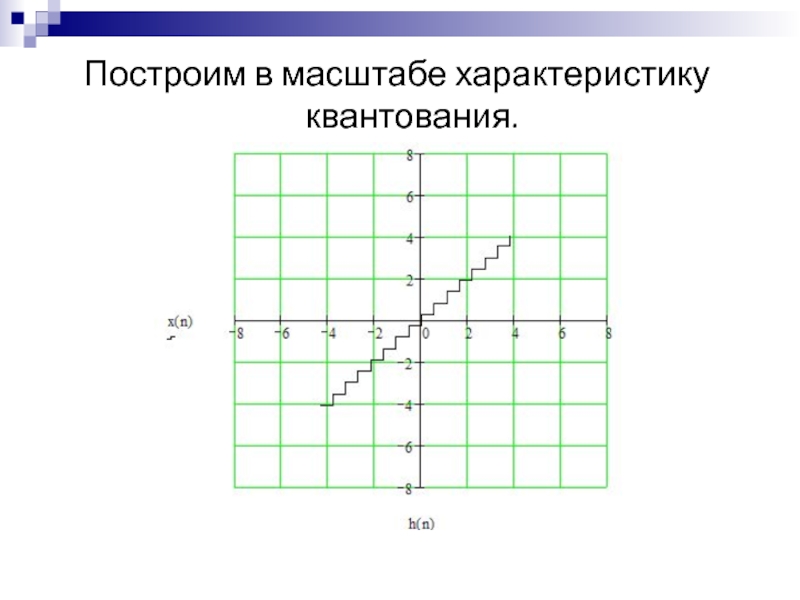
- 37. Построим в масштабе характеристику квантования.
- 38. Задание 5Рассматривая отклик квантователя как случайный дискретный
- 39. Расчетные формулы:Распределение вероятностей:Энтропия равна:
- 40. Производительность или скорость ввода информации в ДКС определяется: Избыточность последовательности источника:
- 41. Квантованная последовательность y=x (n) с учетом
- 42. Максимальная энтропия равна:Избыточность последовательности источника:
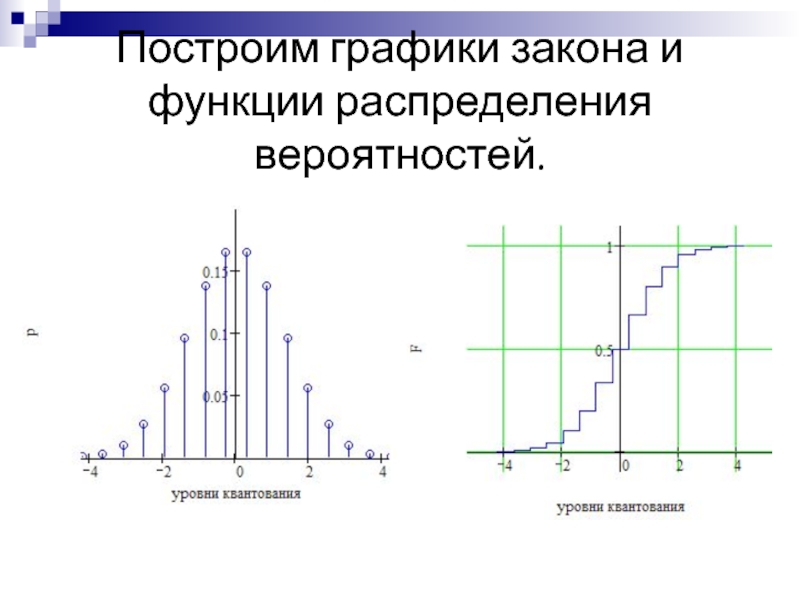
- 43. Построим графики закона и функции распределения вероятностей.
- 44. Задание 6Закодировать значение L- ичного дискретного сигнала
- 45. Расчетные формулы:Априорные вероятности передачи нуля и единицы:Ширина спектра сигнала ИКМ:
- 46. Процедура двоичного безызбыточного блочного кодирования отсчетов X(n):
- 47. ПримерАприорные вероятности передачи нуля и единицы:Рассчитаем ширину
- 48. Задание 7Пологая, что для передачи ИКМ сигнала
- 49. Задание 8Рассматривая НКС как аддитивный гауссовский канал
- 50. построить в масштабе четыре графика функций плотности
- 51. Задание 9С учетом заданного вида приема (детектирования)
- 52. Задание 10Рассматривая отклик декодера ПРУ как случайный
- 53. Задание 11Полагая ФНЧ на выходе ЦАП приемника
- 54. качественно изобразить сигналы на выходе декодера и
- 55. Задание 12В виду того, что выбор начальной
- 56. Привести блок схему программы решения этой задачи
- 57. Выводы:При расчете первых трех заданий ознакомились со
- 58. Выводы:В заданиях № 4-6 при заданных значениях
- 59. Выводы:При выполнении заданий 7, 8, 9 ознакомились
- 60. Контрольные вопросы:Объясните функцию ФНЧ в системе электросвязи.Из
- 61. Контрольные вопросы:Запишите соотношение для мощностей и амплитуд
- 62. Контрольные вопросы:Дайте расшифровку ФПВ.Раскройте понятие энтропии источника.Изобразите
- 63. Контрольные вопросы:Постройте график закона распределения вероятностей отклика
- 64. Скачать презентанцию
Цель курсовой работы состоит в приобретении и развитии навыков и умений анализа помехоустойчивости и эффективности систем передачи информации, а также в ознакомлении с цифровыми методами представления и передачи непрерывных сообщений.Для облегчения
Слайды и текст этой презентации
Слайд 1Курсовая работа по дисциплине: Теория электрической связи «РАСЧЕТ ПРОЦЕССОВ ОБРАБОТКИ СИГНАЛОВ В
ЦИФРОВОЙ СИСТЕМЕ ЭЛЕКТРОСВЯЗИ»
Слайд 2Цель курсовой работы состоит в приобретении и развитии навыков и
умений анализа помехоустойчивости и эффективности систем передачи информации, а также
в ознакомлении с цифровыми методами представления и передачи непрерывных сообщений.Для облегчения решения курсовой работы далее приводятся цели заданий, основные задачи, выводы и контрольные вопросы.
Слайд 3Цели заданий:
В первых трех заданиях курсовой работы необходимо исследовать передачу
и обработку сообщений по системе электросвязи, а именно, преобразование сигнала
из аналоговой формы в цифровую. Убедиться в том, что цифровой сигнал обладает высокой помехоустойчивостью.В заданиях № 4-6 изучить понятия: интервал квантования, порог и уровень квантования. Ознакомиться с видом характеристики квантования, законом и функцией распределения вероятностей. Изучить способы кодирования значений L-ичного дискретного сигнала.
Слайд 4Цели заданий:
В заданиях № 7-9 ознакомиться и изучить схему приемника
сигнала дискретной модуляции и принцип ее работы.
В последних трех заданиях
необходимо рассчитать числовые характеристики (дисперсию, мат. ожидание, скп, распределение вероятностей) на выходе ДКС и ЦАП приемников и решить оптимизационную задачу, привести блок-схему.Слайд 7Источник сообщений – некоторый объект или система, информацию о состоянии
или поведении которого необходимо передать на некоторое расстояние.
ФНЧ – фильтр
нижних частот, ограничивает спектр некоторой верхней частотой Fв.Дискретизатор – преобразовывает отсчеты первичного сигнала в определенные моменты времени непрерывной функции в совокупность мгновенных значений.
Слайд 8Квантователь – осуществляет квантование по уровню дискретизированных отсчетов, т.е. устанавливаются
уровни разрешенные для передачи.
Кодер – преобразует квантованные отсчеты в кодовые
комбинации, обозначающие соответствующие уровни (кодируются двоичным кодом).Слайд 9Модулятор – устройство, предназначенное для согласования источника сообщений с используемой
линией связи, т. е. формирования канального сигнала.
ПДУ – передающее устройство,
предназначенное для предотвращения внеполосных излучений, для фильтрации и усиления канального сигнала и установления требуемого отношения сигнал – шум.Слайд 10Линия связи - совокупность физических цепей, имеющих общую среду распространения
и служащих для передачи электрических сигналов от передатчика к приемнику.
Источник помех - любое мешающее внешнее или внутреннее воздействие на сигнал, вызывающее случайные отклонения принятого сигнала от передаваемого.
Слайд 11ПРУ – принимающее устройство или приемник, предназначенное для фильтрации входного
согнала от помех.
Детектор – выделяет закон изменения информационного параметра, при
этом на выход устанавливается РУ.РУ – решающее устройство, предназначенное для опознавания переданных двоичных символов.
Слайд 12Декодер – устройство, восстанавливающее знаки сообщения из кодовых комбинаций.
Интерполятор –
преобразовывает совокупность известных мгновенных значений сигнала в непрерывную функцию.
ФНЧ –
сглаживает квантованные отсчеты, соединяя близлежащие уровни.Слайд 13Получатель сообщения – некоторый объект или система, принимающая информацию о
состоянии или поведении источника сообщения.
Слайд 14Задание 2
По заданной функции корреляции исходного сообщения:
Рассчитать интервал корреляции, спектр
плотности мощности и начальную энергетическую ширину спектра сообщения;
Построить в масштабе
графики функции корреляции и спектра плотности мощности, отметить на них найденные параметры.Слайд 15Интервал корреляции – промежуток времени между сечениями случайного процессы, в
пределах которого еще наблюдается их статистическая взаимосвязь (корреляция).
Ширина спектра –
та область частот, в которой сосредоточена основная доля энергии сообщения (сигнала).Вспомним, что…
Слайд 17Пример
Исходные данные:
Мощность(дисперсия) сообщения Ра=2,2 ( В2)
Коэффициент затухания α=31 ( С-1)
Показатель
затухания функции ß= α∙103 (С-1)
Функция корреляции
Число уровней квантования L=16
Постоянная
энергетического спектра шума G0=0.003Отношение сигнал-шум по мощности на входе детектора h=4.6
Слайд 18Вычислим интервал корреляции по формуле
Вычислим спектр плотности мощности
получим
предварительно задав
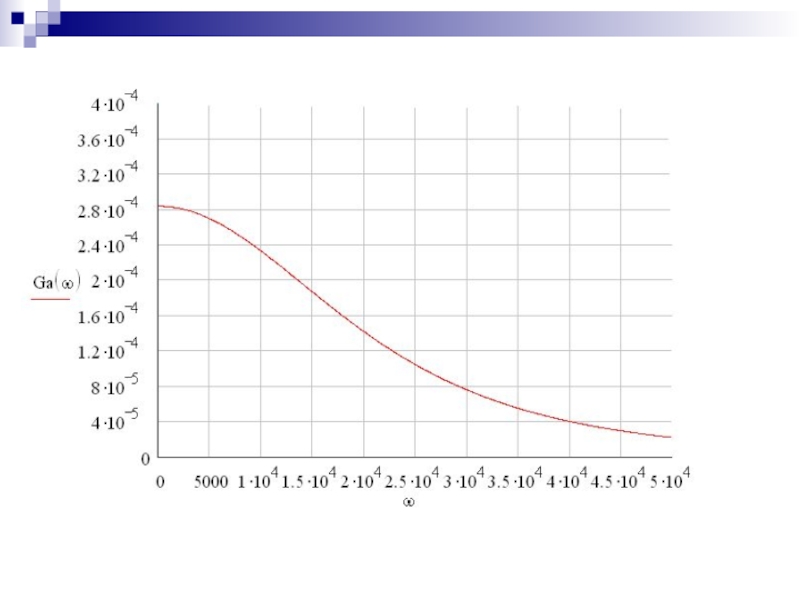
Слайд 19Чтобы определить начальную энергетическую ширину спектра сообщения необходимо определить максимальное
значение энергетического спектра Gmax . Эту величину определяют из графика
зависимости Ga(ω).Зададим предварительно интервал изменения частоты:
ω = 0,5∙10…5∙104
Строим график зависимости спектра плотности мощности от частоты
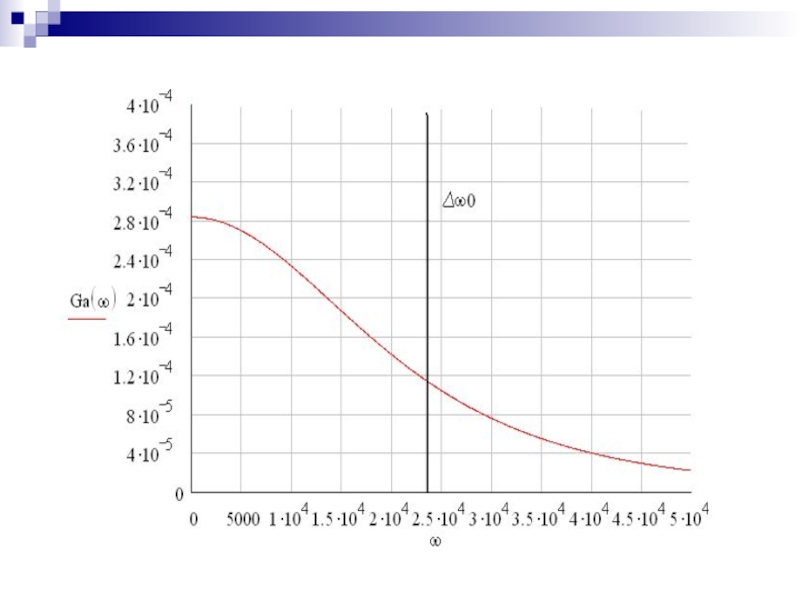
Слайд 21Как видно из графика Gmax=Ga(0) = 2.839∙10-4
Вычислим начальную энергетическую ширину
спектра сообщения по известной формуле:
получим
Обозначим на графике начальную энергетическую ширину
спектраСлайд 24Задание 3
Считая, что исходное сообщение воздействует на идеальный ФНЧ с
единичным коэффициентом передачи и полосой пропускания, равной начальной энергетической ширине
спектра сообщения:Рассчитать среднюю квадратическую погрешность фильтрации (СКПФ) сообщения, среднюю мощность отклика ИФНЧ, частоту и интервал временной дискретизации отклика ИФНЧ;
Качественно, с учетом найденных параметров, изобразить сигналы и спектры на входе и выходе дискретизатора АЦП.
Слайд 25Расчетные формулы:
Средняя мощность отклика ИФНЧ:
Средняя квадратическая погрешность фильтрации (СКПФ):
Слайд 26По предложенным формулам вычислим среднюю мощность отклика ИФНЧ и СКПФ,
получим:
Рх = 1,613 (B2)
СКПФ = 0,58721
Для вычисления частоты дискретизации необходимо
определить верхнюю частоту спектра:где
Слайд 27Получаем, что верхняя частота спектра:
Fв = 3875 Гц
Частота дискретизации в
два раза больше верхней частоты спектра, следовательно:
fд = 2Fв =
7750 ГцИнтервал дискретизации обратно пропорционален частоте дискретизации и равен:
Слайд 28Изобразим графически спектры сигнала на входе и выходе дискретизатора АЦП
На
входе дискретизатора На выходе дискретизатора
АЦП АЦП
Слайд 29Задание 4
Полагая, что последовательность дискретных отсчетов на выходе дискретизатора далее
квантуется по уровню с равномерной шкалой квантования:
Рассчитать интервал квантования, пороги
и уровни квантования, среднюю квадратическую
погрешность квантования (СКПК);Построить в масштабе характеристику квантования.
Слайд 31Средняя квадратическая погрешность квантования.
где PХ и PУ соответственно
мощности(дисперсии) входного и выходного сигналов квантователя; BХУ - коэффициент взаимной
корреляции.Для гауссового процесса:
Слайд 32Коэффициент взаимной корреляции между входным и выходным сигналами квантователя:
Мощность
квантованного процесса:
В результате получаем следующую формулу для среднеквадратической погрешности квантования:
Слайд 33Пример
Напомним, что число уровней квантования L=16.
Определим шаг квантования:
Пороги квантования:
Уровни квантования:
Слайд 34Рассчитаем среднюю квадратическую погрешность квантования (СКПК).
Гауссовский (нормальный) случайный
процесс:
Коэффициент взаимной корреляции между входным и выходным сигналами квантователя.
Слайд 35Распределение вероятностей дискретной случайной величины:
Найдем интегральное распределение вероятностей:
Слайд 36Теперь найдем мощность крантованного процесс:
Средняя квадратическая погрешность квантования:
Слайд 38Задание 5
Рассматривая отклик квантователя как случайный дискретный сигнал с независимыми
значениями на входе L- ичного дискретного канала связи (ДКС):
рассчитать закон
и функцию распределения вероятностей квантованного сигнала, а также энтропию, производительность и избыточность L-ичного дискретного источника;построить в масштабе графики рассчитанных закона и функции распределения вероятностей.
Слайд 40Производительность или скорость ввода информации в ДКС определяется:
Избыточность последовательности
источника:
Слайд 41Квантованная последовательность y=x (n) с учетом независимости её значений
определяется одномерным распределением вероятностей.
Найдем энтропию L-ичного источника:
Найдем производительность L-ичного источника:
Пример
Слайд 44Задание 6
Закодировать значение L- ичного дискретного сигнала двоичным блочным примитивным
кодом, выписать все кодовые комбинации кода и построить таблицу кодовых
расстояний кода; кроме того:рассчитать априорные вероятности передачи по двоичному ДКС символов нуля и единицы, начальную ширину спектра сигнала ИКМ;
изобразить качественно на одном графике сигналы в четырех сечениях АЦП: вход АЦП, выход дискретизатора, выход квантователя, выход АЦП.
Слайд 46Процедура двоичного безызбыточного блочного кодирования отсчетов X(n): Физические уровни X(n),
n=0,L-1, вначале перенумеровываются, т.е. заменяются их номерами X(n)=n, иначе, представляются
в виде десятичных чисел от 0 до 15. Затем эти десятичные числа представляют в двоичной системе счисления с основанием 2.Число кодовых символов:
Слайд 47Пример
Априорные вероятности передачи нуля и единицы:
Рассчитаем ширину спектра сигнала ИКМ:
k1 - постоянная, выбираемая в пределах от 1.5 до 2.
рекомендуется выбрать k1=1.667. Слайд 48Задание 7
Пологая, что для передачи ИКМ сигнала по непрерывному каналу
связи (НКС) используется гармонический переносчик:
рассчитать нормированный к амплитуде переносчика спектр
модулированного сигнала и его начальную ширину спектра;построить в масштабе график нормированного спектра сигнала дискретной модуляции и отметить на нем найденную ширину спектра.
Слайд 49Задание 8
Рассматривая НКС как аддитивный гауссовский канал с ограниченной полосой
частот, равной ширине спектра сигнала дискретной модуляции, и заданными спектральной
плотностью мощности помехи и отношением сигнал-шум:рассчитать приходящиеся в среднем на один двоичный символ мощность и амплитуду модулированного сигнала, дисперсию (мощность) аддитивной помехи в полосе частот сигнала, пропускную способность НКС;
Слайд 50построить в масштабе четыре графика функций плотности вероятностей (ФПВ) мгновенных
значений и огибающих узкополосной гауссовской помехи (УГП) и суммы гармонического
сигнала с УГП.Слайд 51Задание 9
С учетом заданного вида приема (детектирования) сигнала дискретной модуляции:
рассчитать
среднюю вероятность ошибки в двоичном ДКС, скорость передачи информации по
двоичному симметричному ДКС, показатель эффективности передачи сигнала дискретной модуляции по НКС;изобразить схему приемника сигналов дискретной модуляции и коротко описать принцип его работы, пояснить случаи, когда он выносит ошибочные решения.
Слайд 52Задание 10
Рассматривая отклик декодера ПРУ как случайный дискретный сигнал на
выходе L- ичного ДКС:
рассчитать распределение вероятностей дискретного сигнала на выходе
декодера, скорость передачи информации по L- ичному ДКС, относительные потери в скорости передачи информации по L- ичному ДКС;построить в масштабе график закона распределения вероятностей отклика декодера и сравнить его с законом распределения вероятностей отклика квантователя.
Слайд 53Задание 11
Полагая ФНЧ на выходе ЦАП приемника идеальным с полосой
пропускания, равной начальной энергетической ширине спектра исходного сообщения:
рассчитать дисперсию случайных
импульсов шума передачи на выходе интерполятора ЦАП, среднюю квадратическую погрешность шума передачи (СКПШ), суммарную начальную СКП восстановления непрерывного сообщения (ССКП), относительную СКП (ОСКП);Слайд 54качественно изобразить сигналы на выходе декодера и интерполятора ЦАП, а
также восстановленного сообщения на выходе системы электросвязи.
Слайд 55Задание 12
В виду того, что выбор начальной энергетической ширины спектра
исходного сообщения не приводит к минимуму ОСКП, решить оптимизационную задачу:
с помощью ЭВМ определить оптимальную энергетическую ширину спектра сообщения, доставляющую минимум относительной суммарной СКП его восстановления;Слайд 56Привести блок схему программы решения этой задачи на ЭВМ, распечатку
программы, составленную на (выбранном самостоятельно) алгоритмическом языке, а также распечатку
графика зависимости ОСКП от энергетической ширины спектра сообщения.Слайд 57Выводы:
При расчете первых трех заданий ознакомились со структурной схемой электросвязи,
изучили функцию корреляции, рассчитали интервал корреляции, спектр плотности мощности и
начальную энергетическую ширину спектра плотности сообщения, построили графики. Также в процессе выполнения заданий 1, 2, 3 рассчитали СКПФ сообщения, среднюю мощность отклика ИФНЧ и изобразили сигналы и спектры на входе и выходе дискретизатора ЦАП.Слайд 58Выводы:
В заданиях № 4-6 при заданных значениях числа уровней квантования
и средней мощности отклика рассчитали интервал, пороги и уровни квантования.
Изучили характеристики квантования, определили энтропию и функцию распределения вероятностей. Также рассчитали априорные вероятности передачи по двоичному ДКС, начальную ширину спектра сигнала ИКМ и построили графики.Слайд 59Выводы:
При выполнении заданий 7, 8, 9 ознакомились с принципами расчета
характеристик и параметров сигналов дискретной модуляции, узкополосного непрерывного гауссовского канала
связи, а также научились оценивать помехоустойчивость и эффективность приема сигналов дискретной модуляции.В процессе выполнения заданий 10.11,12 изучили числовые характеристики сигнала, рассчитали погрешности (СКПП, ССКП, ОСКП). Качественно изобразили графики, привели блок-схему программы решения оптимизационной задачи на алгоритмическом языке.
Слайд 60Контрольные вопросы:
Объясните функцию ФНЧ в системе электросвязи.
Из каких элементов состоит
АЦП?
Напишите формулу расчета интервала корреляции и формулу для определения спектральной
плотности.Что такое средняя квадратическая погрешность фильтрации (СКПФ)?
Изобразите качественный вид спектра на выходе дискретизатора АЦП.
Слайд 61Контрольные вопросы:
Запишите соотношение для мощностей и амплитуд в среднем приходящихся
на один двоичный символ для сигналов: ДАМ, ДЧМ, ДФМ.
Нарисуйте графики
сигналов: ДАМ, ДЧМ, ДФМ.Запишите выражения по которым строят амплитудные спектры сигналов дискретной модуляции.
Напишите формулу для определения скорости передачи информации по дискретному каналу связи.
Напишите выражение для определения энтропии ошибочных решений.
Слайд 62Контрольные вопросы:
Дайте расшифровку ФПВ.
Раскройте понятие энтропии источника.
Изобразите спектр сигнала на
выходе квантователя.
Запишите выражение для нахождения избыточности.
По какой формуле строится таблица
кодовых расстояний?Слайд 63Контрольные вопросы:
Постройте график закона распределения вероятностей отклика декодера.
Напишите формулу скорости
передачи информации по L-ичному ДКС.
Постройте график восстановления сообщения на выходе
системы электросвязи.Напишите формулу для расчета дисперсии случайных импульсов шума передачи.
Постройте график зависимости ОСКП фильтрации, квантования, передачи от энергетической ширины спектра сообщений.