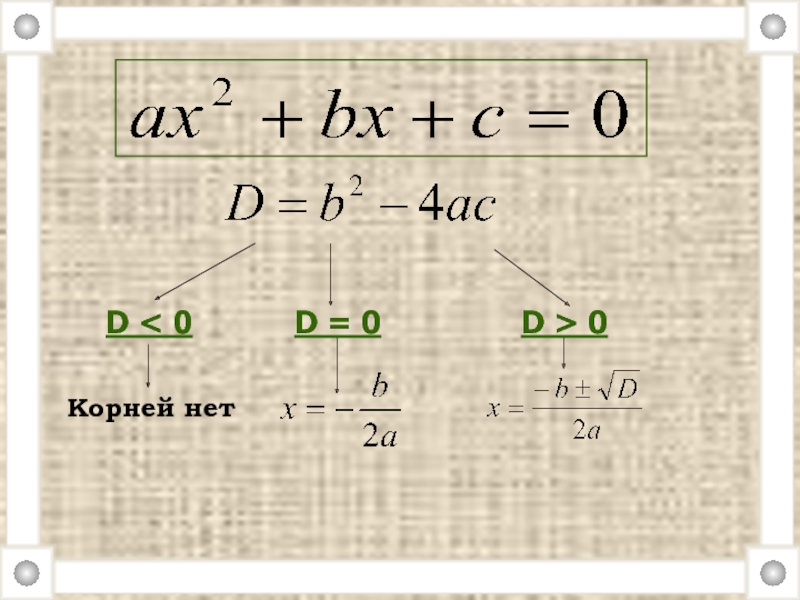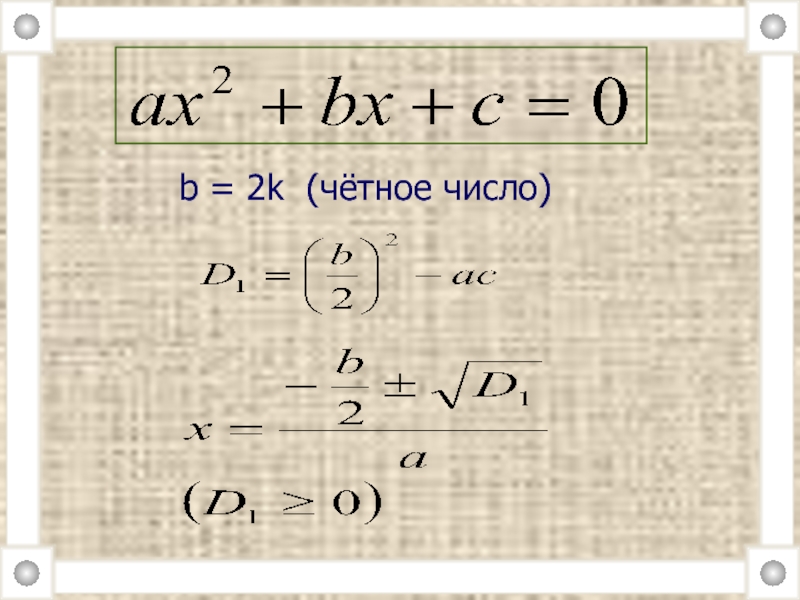Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Квадратные уравнения - методы решения
Содержание
- 1. Квадратные уравнения - методы решения
- 2. «Уравнение - это золотой ключ, открывающий все математические сезамы». С. Коваль.
- 3. 1. Теоретическая разминка.2. Энциклопедия квадратных уравнений.3. Думающий колпак. 4. Историческая справка.5. Копилка ценных мыслей.6. Домашнее задание.
- 4. Сформулируйте определение квадратного уравнения.2. Объясните, в
- 5. 1. Метод выделения квадрата двучлена.2. Метод «переброски» старшего коэффициента.3. На основании теорем.
- 6. Большим и указательным пальцами мягко оттягивают
- 7. Слайд 7
- 8. Слайд 8
- 9. Слайд 9
- 10. В 13 – 16 веках
- 11. Решите уравнение 3х2 + 5х + 2
- 12. подробнее
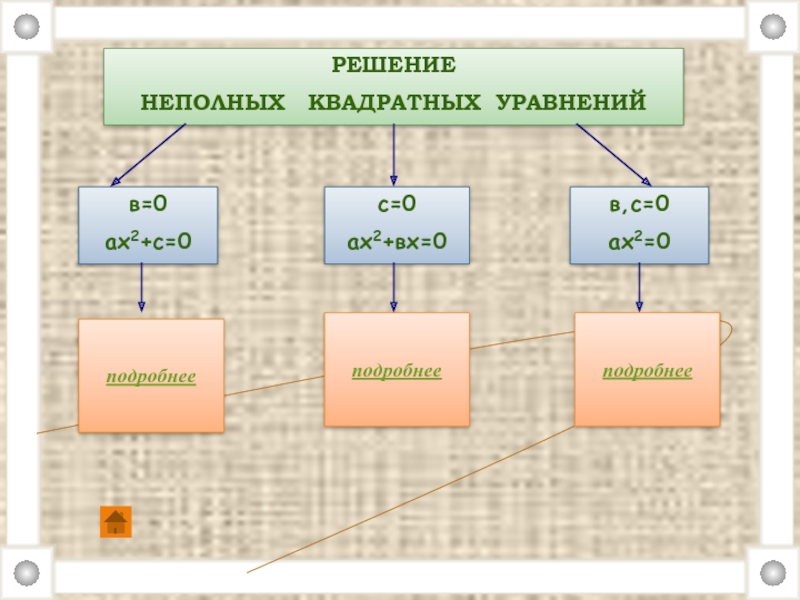
- 13. РЕШЕНИЕ НЕПОЛНЫХ КВАДРАТНЫХ УРАВНЕНИЙв=0ах2+с=0с=0ах2+вх=0в,с=0ах2=0подробнееподробнееподробнее
- 14. Алгоритм решения 1.Переносим с в правую часть
- 15. Выносим x за скобки:
- 16. 1. Делим обе части уравнения на а≠0.х2 = 02. Одно решение: х = 0.Алгоритм решенияПодведём итог!в,с=0ах2=0
- 17. Неполные квадратные уравнения:
- 18. D < 0D = 0D > 0Корней нет
- 19. b = 2k (чётное число)
- 20. x1 и х2 – корни уравнения x1 и х2 – корни уравнения
- 21. Суть метода:
- 22. Корни квадратных уравнений и связаны соотношениямииПример:Метод «переброски» старшего коэффициента.подробнее2х2 - 9х – 5 = 0.
- 23. На основании теорем: Если в квадратном уравнении a+b+c=0,
- 24. Метод выделения квадрата двучлена. (a +
- 25. Метод “переброски” старшего коэффициента ax2 +
- 26. Теорема 1. Если в квадратном уравнении
- 27. Теорема 2. Если в квадратном уравнении
- 28. Метод разложения на множители.Решите уравнение 4х2 +
- 29. 3. в=0ах2+с=02. с=0ах2+вх=01. в,с=0ах2=04. b - нечётноеах2+bx+с=05.
- 30. Слайд 30
- 31. Математик немного поэт. Т. Вейерштрасс
- 32. Скачать презентанцию
Слайды и текст этой презентации
Слайд 3
1. Теоретическая разминка.
2. Энциклопедия квадратных уравнений.
3. Думающий колпак.
4. Историческая
справка.
Слайд 4Сформулируйте определение квадратного уравнения.
2. Объясните, в чём заключается смысл
ограничения в определении квадратного уравнения (а ≠ 0).
3. Перечислите
виды квадратных уравнений.4. Какое квадратное уравнение называется неполным? Приведите пример.
5. Какое квадратное уравнение называется приведённым? Приведите пример.
6. Способы решения полного квадратного уравнения?
подробнее
подробнее
Слайд 5
1. Метод выделения квадрата двучлена.
2. Метод «переброски» старшего коэффициента.
3. На
основании теорем.
Слайд 6
Большим и указательным пальцами мягко оттягивают назад и прижимают, массируя,
раковины ушей.
УЧЕБНЫЕ ИНСТРУКЦИИ
• Держите голову прямо, чтобы подбородку
было удобно.
• Упражнение повторяют трижды или более раз.
Слайд 8
.
Впервые ввёл термин «квадратное уравнение» немецкий философ
- знаменитый немецкий философ, родился в 1679 г. в Бреславле, в семье простого ремесленника, изучал в Йене сначала богословие, потом математику и философию.Кристиан Вольф.
Кристиан Вольф -
Слайд 10 В 13 – 16 веках даются отдельные методы
решения различных видов квадратных уравнений. Слияние этих методов произвел в
1544 году немецкий математик –Это было настоящее событие в математике.
Михаэль Штифель.
Слайд 11
Решите уравнение 3х2 + 5х + 2 = 0:
используя
формулу дискриминанта – «3»,
двумя способами – «4»,
тремя способами
– «5».Дополнительно.
Решите уравнение (х2-х)2 - 14(х2-х) + 24 = 0 методом введения новой переменной.
Слайд 13
РЕШЕНИЕ
НЕПОЛНЫХ КВАДРАТНЫХ УРАВНЕНИЙ
в=0
ах2+с=0
с=0
ах2+вх=0
в,с=0
ах2=0
подробнее
подробнее
подробнее
Слайд 14Алгоритм решения
1.Переносим с в правую часть уравнения.
ах2 = -с.
2.Делим
обе части уравнения на а≠0.
х2= .
3.Если
>0 - два решения:х1 = и х2 = -
Если <0 - нет решений.
в=0
ах2+с=0
Слайд 15
Выносим x за скобки:
х (ах +
в) = 0.
2. «Разбиваем» уравнение
на два:
x
= 0, ах + в = 0.3. Два решения:
х = 0 и х = (а≠0).
Алгоритм решения
с=0
ах2+вх=0
Слайд 16
1. Делим обе части уравнения на а≠0.
х2 = 0
2. Одно
решение: х = 0.
Алгоритм решения
Подведём итог!
в,с=0
ах2=0
Слайд 21
Суть метода: привести квадратное уравнение
общего вида к неполному квадратному уравнению.
Пример: х2 - 6х + 5 = 0.Метод выделения квадрата двучлена.
подробнее
Слайд 22Корни квадратных уравнений
и
связаны соотношениями
и
Пример:
Метод «переброски» старшего коэффициента.
подробнее
2х2 -
9х – 5 = 0.
Слайд 23На основании теорем:
Если в квадратном уравнении a+b+c=0, то один из
корней равен 1, а
второй по теореме Виета
равен Если в квадратном уравнении a+c=b, то один из корней равен (-1),
а второй по теореме Виета равен
Примеры:
подробнее
200х2 + 210х + 10 = 0.
Слайд 24Метод выделения квадрата двучлена.
(a + b)2 = a2 +
2ab + b2,
(a - b)2 = a2 - 2ab
+ b2.Решим уравнение х2 - 6х + 5 = 0.
х2 - 6х + 5 = 0.
(х -3)2 – 4 = 0.
(х -3)2 = 4.
х – 3 = 2; х – 3 = -2.
х = 5, х =1.
Ответ: 5; 1.
Слайд 25Метод “переброски” старшего коэффициента
ax2 + bx + c =
0 и y2+ by + ac = 0
связаны соотношениями:
Решите
уравнение 2х2 - 9х – 5 = 0.у2 - 9у - 10 = 0.
D>0, по теореме, обратной теореме Виета, получаем корни: -1; 10,
далее возвращаемся к корням исходного уравнения: - 0,5; 5.
Ответ: 5; -0,5.
Слайд 26Теорема 1. Если в квадратном уравнении a + b +
c = 0, то один из корней равен 1, а
второй по теореме Виета равенРешите уравнение 137х2 + 20х – 157 = 0.
137х2 + 20х – 157 = 0.
a = 137, b = 20, c = -157.
a + b+ c = 137 + 20 – 157 =0.
x1 = 1,
Ответ: 1; .
.
Слайд 27Теорема 2. Если в квадратном уравнении a + c =
b, то один из корней равен (-1), а второй по
теореме Виета равенРешите уравнение 200х2 + 210х + 10 = 0.
200х2 + 210х + 10 = 0.
a = 200, b = 210, c = 10.
a + c = 200 + 10 = 210 = b.
х1 = -1, х2 = -
Ответ: -1; -0,05
Слайд 28Метод разложения на множители.
Решите уравнение 4х2 + 5х + 1
= 0.
4х2 + 5х + 1 = 0.
4х2 + 4х
+ х + 1 = 0.4х(х+1) + (х+1) = 0.
4х(х + 1) = 0.
Произведение двух множителей равно нулю, если хотя бы один из них равен нулю, а второй при этом не теряет смысла, или когда оба равны нулю.
4х = 0, х + 1 = 0.
х = 0, х = -1.
Ответ: 0; -1.
Слайд 29
3. в=0
ах2+с=0
2. с=0
ах2+вх=0
1. в,с=0
ах2=0
4. b - нечётное
ах2+bx+с=0
5. b - чётное
ах2+bx+с=0
6.
Теорема Виета.
7. Метод выделения квадрата двучлена.
8. Метод «переброски» старшего коэффициента.
9.
Т1 или Т2.10. Метод разложения на множители.
11. Метод введения новой переменной.