Lecture 5. Linear Regression. Regression model evaluation metrics

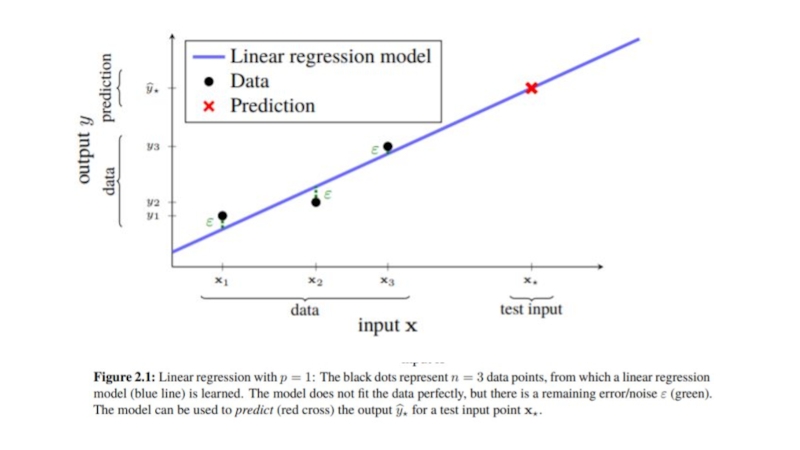
output variable y (a scalar) as an affine combination of

the input variables x1, x2, . . . , xp (each a scalar) plus a noise term ε,


(1)

We refer to the coefficients β0, β1, . . . βp as the parameters in the model, and we sometimes refer to β0 specifically as the intercept term. The noise term ε accounts for non-systematic, i.e., random, errors between the data and the model. The noise is assumed to have mean zero and to be independent of x. Machine learning is about training, or learning, models from data.
Regression to predict future outputs for inputs that we have not yet seen.

emphasis is rather on predicting some (not yet seen) output

y*? for some new input x* = [x*1 x*2 . . . x*p ] T. To make a prediction for a test input x* , we insert it into the model (1). Since ε (by assumption) has mean value zero, we take the prediction as



We use the symbol ^ on y * to indicate that it is a prediction, our best guess. If we were able to somehow observe the actual output from x *, we would denote it by y * (without a hat).

accuracy is an essential part of the process in creating

machine learning models to describe how well the model is performing in its predictions. Evaluation metrics change according to the problem type.
   The errors represent how much the model is making mistakes in its prediction. The basic concept of accuracy evaluation is to compare the original target with the predicted one according to certain metrics.

the total difference between the predicted values and the actual

ones is relatively small, the total error/loss will be smaller value and thus, signify a good model.
A Larger Loss Value If the difference between the actual and predicted values is large, the total error/value of loss function will be relatively larger as well to imply that the model is not trained well.

training a Regression Model is to find those values of

weights against which loss function can be minimized i. e difference between the predicted values and the true labels is minimized as much as possible.

are to the fitted regression line. It is also known

as the coefficient of determination, or the coefficient of multiple determination for multiple regression.
The definition of R-squared is fairly straight-forward; it is the percentage of the response variable variation that is explained by a linear model. Or:
R-squared = Explained variation / Total variation
R-squared is always between 0 and 100%:
0% indicates that the model explains none of the variability of the response data around its mean.
100% indicates that the model explains all the variability of the response data around its mean.
In general, the higher the R-squared, the better the model fits your data.

the variance while the one on the right accounts for

87.4%. The more variance that is accounted for by the regression model the closer the data points will fall to the fitted regression line. Theoretically, if a model could explain 100% of the variance, the fitted values would always equal the observed values and, therefore, all the data points would fall on the fitted regression line.