Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Лектор Янущик О.В. 20 1 3 г. Математический анализ Раздел: Определенный
Содержание
- 1. Лектор Янущик О.В. 20 1 3 г. Математический анализ Раздел: Определенный
- 2. ГЛАВА I. Определенный интеграл и его приложения
- 3. ЗАДАЧА 1 (о площади криволинейной трапеции). Пусть
- 4. ЗАДАЧА 2 (о пройденном пути). Пусть точка
- 5. 2. Определенный интеграл: определение и условие его
- 6. Пусть Число I называется пределом интегральных сумм
- 7. Функция f(x), для которой на [a;b] существует определенный
- 8. Замечание. Определяя определенный интеграл, полагали a b , то 2)
- 9. 3. Свойства определенного интеграла 1) Геометрический смысл
- 10. ДОКАЗАТЕЛЬСТВО4) Постоянный множитель k (k 0) можно выносить
- 11. 6) Если отрезок интегрирования [a;b] разбит точкой c
- 12. 9) Следствие свойств 8 и 3. Если
- 13. 11) Теорема о среднем. Если функция f(x) непрерывна на
- 14. §2. Вычисление определенных интегралов 1. Интеграл с
- 15. ТЕОРЕМА 1 (о производной определенного интеграла по
- 16. Имеем: Φ(x) – первообразная для функции f(x)
- 17. Полагая x = b получаем: (2)Формула (2) называется формулой Ньютона
- 18. Скачать презентанцию
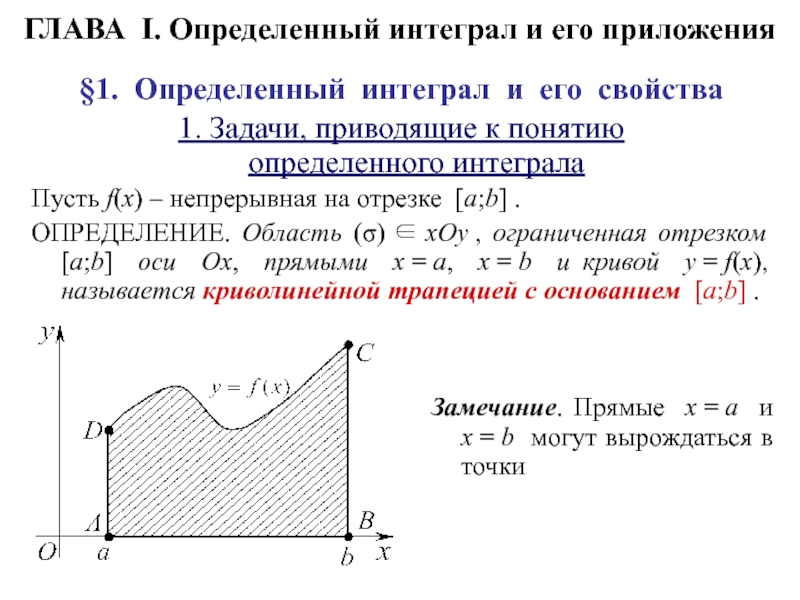
ГЛАВА I. Определенный интеграл и его приложения §1. Определенный интеграл и его свойства1. Задачи, приводящие к понятию определенного интеграла Пусть f(x) – непрерывная на отрезке [a;b] .ОПРЕДЕЛЕНИЕ. Область (σ) xOy , ограниченная отрезком
Слайды и текст этой презентации
Слайд 1 Лектор Янущик О.В.
2013 г.
Математический анализ
Раздел: Определенный
интеграл
Формула Ньютона - ЛейбницаСлайд 2ГЛАВА I. Определенный интеграл и его приложения
§1. Определенный интеграл
и его свойства
1. Задачи, приводящие к понятию
определенного интеграла
Пусть
f(x) – непрерывная на отрезке [a;b] .ОПРЕДЕЛЕНИЕ. Область (σ) xOy , ограниченная отрезком [a;b] оси Ox, прямыми x = a, x = b и кривой y = f(x), называется криволинейной трапецией с основанием [a;b] .
Замечание. Прямые x = a и x = b могут вырождаться в точки
Слайд 3ЗАДАЧА 1 (о площади криволинейной трапеции).
Пусть f(x) 0 , x[a;b] .
Найти площадь
S криволинейной трапеции (σ) .
Если Δxi = xi – xi–1 – длина отрезка [xi–1 ; xi] ,
то Пусть = max | [xi–1 ; xi] | . Тогда
Слайд 4ЗАДАЧА 2 (о пройденном пути).
Пусть точка движется по кривой
и ее скорость изменяется по закону v = f(t).
Найти путь S,
пройденный точкой за промежуток времени [T1 ; T2] .РЕШЕНИЕ.
1) Разобьем [T1 ; T2] на n частей точками
t0 = T1 , t1 , t2 , … , tn = T2 (где t0 < t1 < t2 < … < tn )
2) Выберем на [ti–1 ; ti] (i = 1,2,…n) произвольную точку i .
Если [ti–1; ti] мал, то можно считать, что точка двигалась в те- чение этого времени равномерно со скоростью f(i) .
пройденное расстояние: f(i) Δti , где Δti = ti – ti–1 .
3) Пусть = max | [ti–1; ti] | . Тогда
Слайд 52. Определенный интеграл: определение и условие его существования
Пусть f(x)
задана на отрезке [a;b] .
ОПРЕДЕЛЕНИЕ.
1) Разобьем [a;b] на n частей точками
x0 = a , x1 , x2 , … , xn = b ,
где x0
каждом отрезке [xi–1 ; xi] (i = 1,2,…n) выберем про-
извольную точку i и найдем произведение f(i) Δxi ,
где Δxi = xi – xi–1 – длина отрезка [xi–1 ; xi].
Сумма
называется интегральной суммой для функции f(x) на отрезке [a;b] .
Слайд 6Пусть
Число I называется пределом интегральных сумм In(xi,i) при
0 , если для любого >0 существует >0
такое, что для любого разбиения отрезка [a;b] у которого < , при любом выборе точек i выполняется неравенство| In(xi,i) – I | < .
Если существует предел интегральных сумм In(xi,i) при 0, то его называют определенным интегралом от функции f(x) на отрезке [a;b] (или в пределах от a до b).
ОБОЗНАЧАЮТ:
Называют: [a;b] – промежуток интегрирования,
a и b – нижний и верхний предел интегрирования,
f(x) – подынтегральная функция,
f(x)dx – подынтегральное выражение,
x – переменная интегрирования.
Слайд 7Функция f(x), для которой на [a;b] существует определенный интеграл, называется интегрируемой
на этом отрезке.
ТЕОРЕМА 1 (необходимое условие интегрируемости функции на
[a;b]). Если функция f(x) интегрируема на отрезке [a;b] , то она на этом отрезке ограничена.
ТЕОРЕМА 2 (достаточное условие интегрируемости функции на [a;b]).
Для интегрируемости функции f(x) на [a;b] , достаточно выполнения одного из условий:
1) f(x) непрерывна на [a;b];
2) f(x) ограничена на [a;b] и имеет на [a;b] конечное число точек разрыва;
3) f(x) монотонна и ограничена на [a;b].
Слайд 8Замечание. Определяя определенный интеграл, полагали a b ,
то
2) если a = b , то
Такое расширение определения согласуется с определением
определенного интеграла и его геометрическим (физическим) смыслом. Слайд 93. Свойства определенного интеграла
1) Геометрический смысл определенного интеграла.
Если f(x)
– непрерывна на [a;b] и f(x) 0 , x[a;b] , то
где S
– площадь криволинейной трапеции с основанием [a;b] и ограниченной сверху кривой y = f(x). 2) Физический смысл определенного интеграла
Если функция v = f(t) задает скорость движущейся точки в момент времени t , то
определяет путь S, пройденный точкой за промежуток времени [T1 ; T2] .
Слайд 10ДОКАЗАТЕЛЬСТВО
4) Постоянный множитель k (k 0) можно выносить за знак определенного
интеграла, т.е.
ДОКАЗАТЕЛЬСТВО
5) Определенный интеграл от алгебраической суммы двух (конечного числа)
функций равен алгебраической сумме интегралов от этих функций:ДОКАЗАТЕЛЬСТВО
Слайд 116) Если отрезок интегрирования [a;b] разбит точкой c на две части
[a;c] и [c;b], то
(1)
Замечание. Формула (1) будет иметь место и
в том случае, когда точка c лежит не внутри отрезка [a;b], а вне его. 7) Если f(x) > 0 (f(x) 0) x[a;b] , то
8) Если f(x) (x) x[a;b] , то
ДОКАЗАТЕЛЬСТВО – самостоятельно
Слайд 129) Следствие свойств 8 и 3.
Если m и M
– соответственно наименьшее и наибольшее значения функции f(x) на отрезке
[a;b], то10) Если f(x) – нечетная функция, то
Если f(x) – четная функция, то
Слайд 1311) Теорема о среднем.
Если функция f(x) непрерывна на [a;b], то в
интервале (a;b) найдется такая точка c, что справедливо равенство
ДОКАЗАТЕЛЬСТВО
Слайд 14§2. Вычисление определенных интегралов
1. Интеграл с переменным верхним пределом.
Формула
Ньютона-Лейбница
Пусть f(t) непрерывна на [a;b].
Тогда f(t) непрерывна на
[a;x], где a x b . f(t) интегрируема на [a;x], где a x b .
Рассмотрим интеграл
Имеем: , D(Φ(x)) = [a;b] .
Слайд 15ТЕОРЕМА 1 (о производной определенного интеграла по пере- менному верхнему пределу).
Функция Φ(x) дифференцируема на [a;b], причем
Φ (x) = f(x) .
ДОКАЗАТЕЛЬСТВО
СЛЕДСТВИЕ 2. Любая непрерывная на
[a;b] функция имеет на [a;b] первообразную. Слайд 16Имеем: Φ(x) – первообразная для функции f(x) на [a;b] .
Пусть F(x)
– еще одна первообразная для f(x) на [a;b] .
Тогда F(x)
и Φ(x) будут отличаться постоянным слагаемым(см. §23 теорема 2, I семестр), т.е.
(1)
где a x b , C – некоторое число.
Полагаем x = a . Тогда из (1) получим
0 = F(a) + C ,
C = – F(a) .
Следовательно, (1) можно переписать в виде
Слайд 17Полагая x = b получаем:
(2)
Формула (2) называется формулой Ньютона – Лейбница.
Разность F(b) – F(a)
принято сокращенно записывать в виде
Символ называют
знаком двойной подстановки. Используя это обозначение, формулу (2) можно переписать в виде
Замечание. В формуле (2) можно взять любую из перво- образных функции f(x), так как F(b) – F(a) не зависит от выбора первообразной.

![Лектор Янущик О.В.
20 1 3 г.
Математический анализ
Раздел: Определенный ЗАДАЧА 1 (о площади криволинейной трапеции). Пусть f(x) 0 , x[a;b] . Найти площадь S ЗАДАЧА 1 (о площади криволинейной трапеции). Пусть f(x) 0 , x[a;b] . Найти площадь S криволинейной трапеции (σ) . Если Δxi = xi – xi–1 –](/img/thumbs/4c80d1c43df66314f070fd27aca8efda-800x.jpg)

![Лектор Янущик О.В.
20 1 3 г.
Математический анализ
Раздел: Определенный 2. Определенный интеграл: определение и условие его существования Пусть f(x) задана 2. Определенный интеграл: определение и условие его существования Пусть f(x) задана на отрезке [a;b] .ОПРЕДЕЛЕНИЕ. 1) Разобьем [a;b] на n](/img/thumbs/b951d64bd3ea4132d22e14f69757f92a-800x.jpg)

![Лектор Янущик О.В.
20 1 3 г.
Математический анализ
Раздел: Определенный Функция f(x), для которой на [a;b] существует определенный интеграл, называется интегрируемой на Функция f(x), для которой на [a;b] существует определенный интеграл, называется интегрируемой на этом отрезке. ТЕОРЕМА 1 (необходимое условие](/img/thumbs/0786a4cb99cdbe5cfee16088f540961d-800x.jpg)

![Лектор Янущик О.В.
20 1 3 г.
Математический анализ
Раздел: Определенный 3. Свойства определенного интеграла 1) Геометрический смысл определенного интеграла. Если f(x) – 3. Свойства определенного интеграла 1) Геометрический смысл определенного интеграла. Если f(x) – непрерывна на [a;b] и f(x) 0 , x[a;b] ,](/img/thumbs/037ca28207e00e12d35f563072407bfc-800x.jpg)

![Лектор Янущик О.В.
20 1 3 г.
Математический анализ
Раздел: Определенный 6) Если отрезок интегрирования [a;b] разбит точкой c на две части [a;c] 6) Если отрезок интегрирования [a;b] разбит точкой c на две части [a;c] и [c;b], то (1)Замечание. Формула (1) будет](/img/thumbs/822121012ebc0e9ddc8ebd23867572ae-800x.jpg)

![Лектор Янущик О.В.
20 1 3 г.
Математический анализ
Раздел: Определенный 11) Теорема о среднем. Если функция f(x) непрерывна на [a;b], то в интервале 11) Теорема о среднем. Если функция f(x) непрерывна на [a;b], то в интервале (a;b) найдется такая точка c, что](/img/thumbs/35bdef96034ef553f4db27057b046b2d-800x.jpg)
![Лектор Янущик О.В.
20 1 3 г.
Математический анализ
Раздел: Определенный §2. Вычисление определенных интегралов 1. Интеграл с переменным верхним пределом. Формула §2. Вычисление определенных интегралов 1. Интеграл с переменным верхним пределом. Формула Ньютона-Лейбница Пусть f(t) непрерывна на [a;b].](/img/thumbs/e53e28175e9d5e188e42e0deba0fb3a8-800x.jpg)
![Лектор Янущик О.В.
20 1 3 г.
Математический анализ
Раздел: Определенный ТЕОРЕМА 1 (о производной определенного интеграла по пере- менному верхнему пределу). ТЕОРЕМА 1 (о производной определенного интеграла по пере- менному верхнему пределу). Функция Φ(x) дифференцируема на [a;b], причемΦ (x) = f(x) .ДОКАЗАТЕЛЬСТВОСЛЕДСТВИЕ](/img/thumbs/ecbb66922b08b28ec4059e3d06a5c605-800x.jpg)
![Лектор Янущик О.В.
20 1 3 г.
Математический анализ
Раздел: Определенный Имеем: Φ(x) – первообразная для функции f(x) на [a;b] .Пусть F(x) – Имеем: Φ(x) – первообразная для функции f(x) на [a;b] .Пусть F(x) – еще одна первообразная для f(x) на](/img/thumbs/bde35fc1f8bb68062abcd2cbd7c6924a-800x.jpg)




















