равномерного распределения энергии по степеням свободы.
Первое начало термодинамики.
Теплоемкость.
Уравнение Майера. Теплоемкость твердых тел. Закон Дюлонга-Пти. Адиабатический процесс, политропический процесс и его частные случаи, обратимые и необратимые процессы.
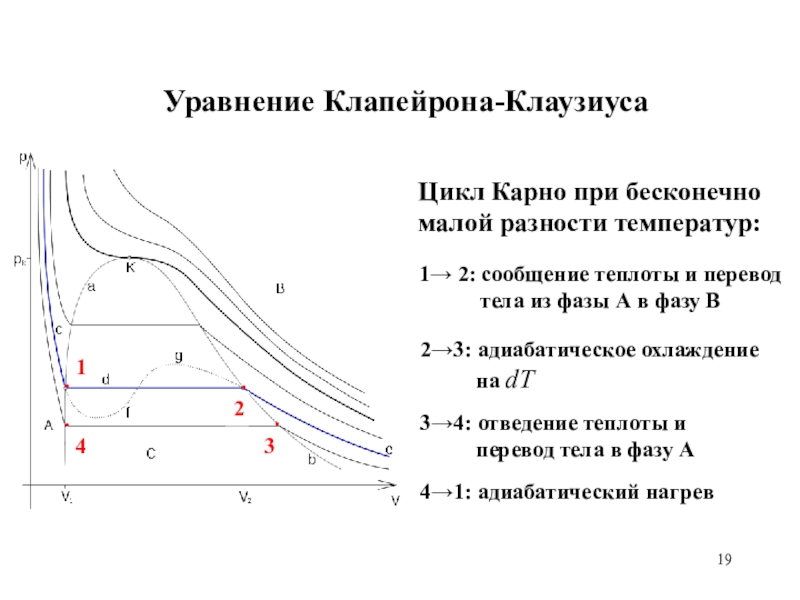
Преобразование теплоты в механическую работу. Цикл Карно и его коэффициент полезного действия.