Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Лекция 1 3
Содержание
- 1. Лекция 1 3
- 2. Способ вспомогательного проецированияВ этом способе используются дополнительные
- 3. Решение: 1. Найдем проекцию луча АА°(S‘)
- 4. 2. Поведем параллельно полученной проекции S‘2 прямую,
- 5. 3. Прямая КЕ перпендикулярна П2, следовательно тень
- 6. 4. Прямая КЕ параллельна П1, следовательно тень
- 7. Криволинейный участок контура собственной тени К-М1 цилиндра дает кривой участок падающей тени К1°- М1°. Е≡Е°2S‘S‘1S‘2●1°К°1П2S‘2M1≡M1°
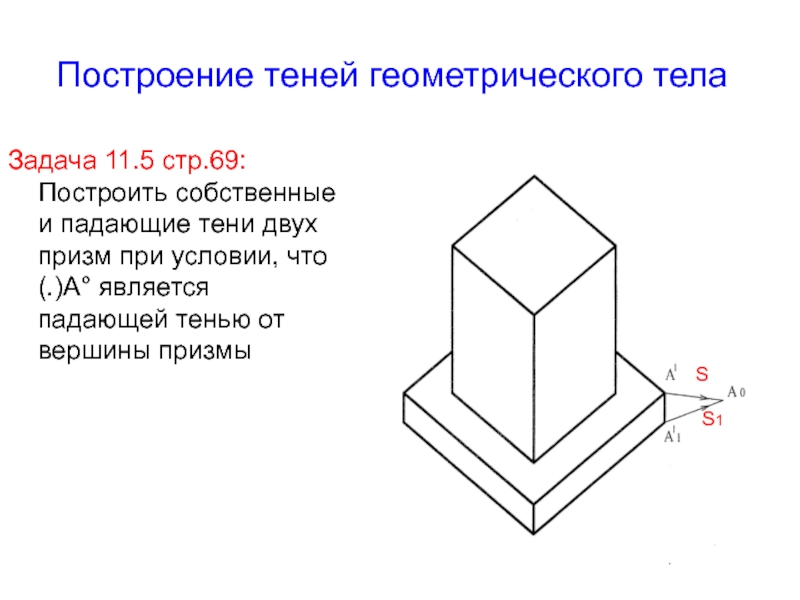
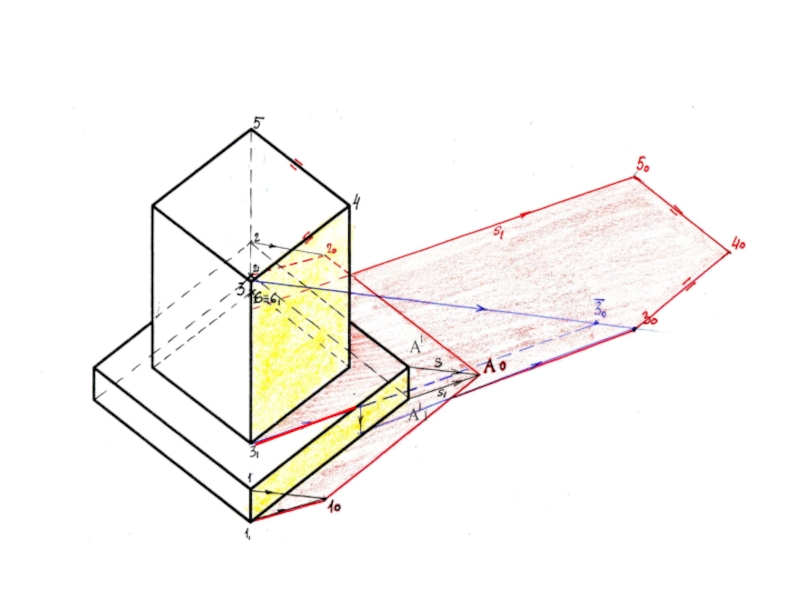
- 8. Построение теней геометрического телаЗадача 11.5 стр.69: Построить
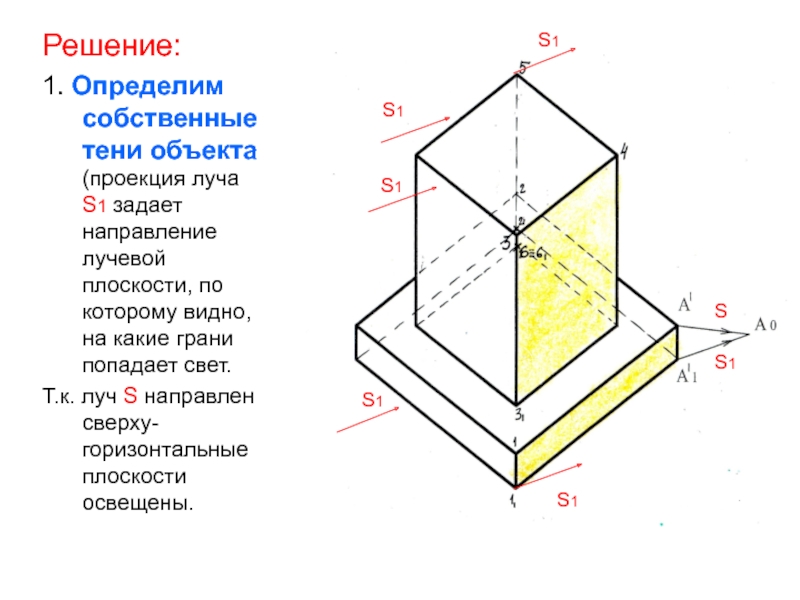
- 9. Решение: 1. Определим собственные тени объекта (проекция
- 10. В собственной тени находятся правые боковые и
- 11. 2. Находим падающие тени от нижнего объема:
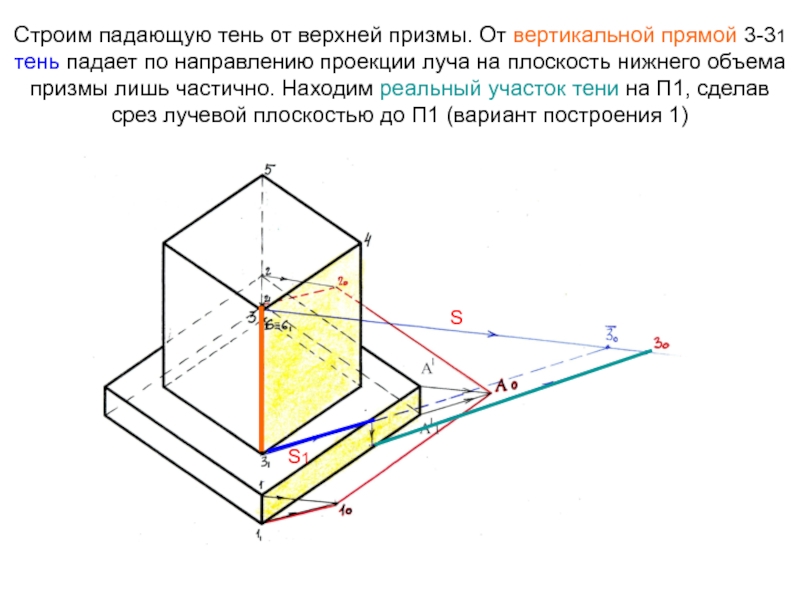
- 12. Строим падающую тень от верхней призмы. От
- 13. Вариант построения 2: срез лучевой плоскостью до
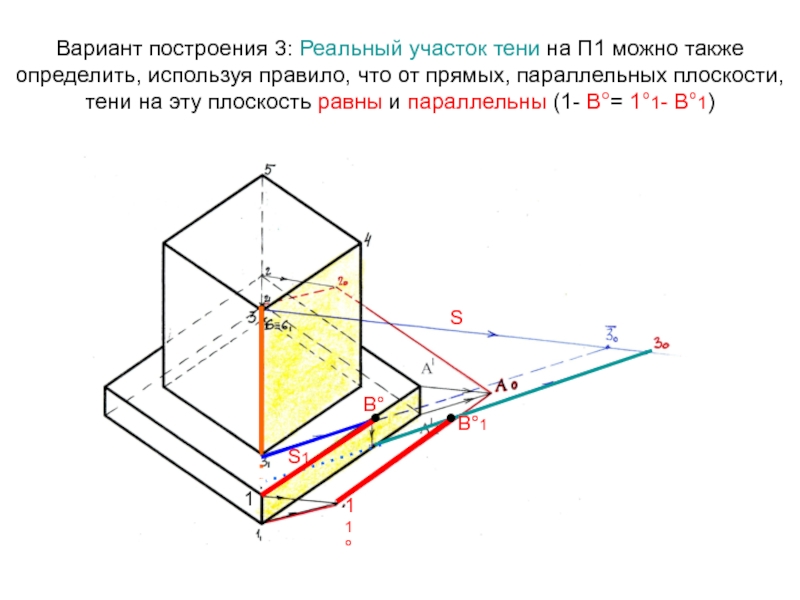
- 14. Вариант построения 3: Реальный участок тени на
- 15. Прямые 3-4 и 4-5 параллельны П1, следовательно
- 16. Слайд 16
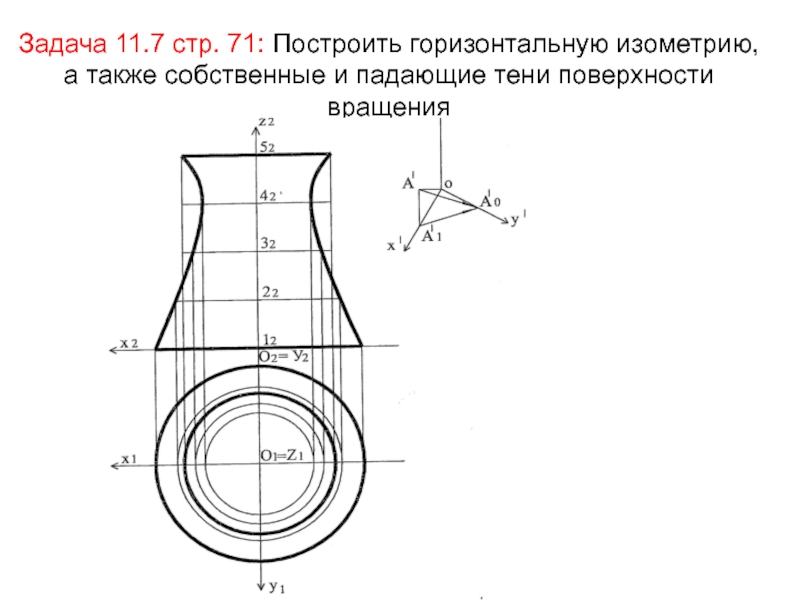
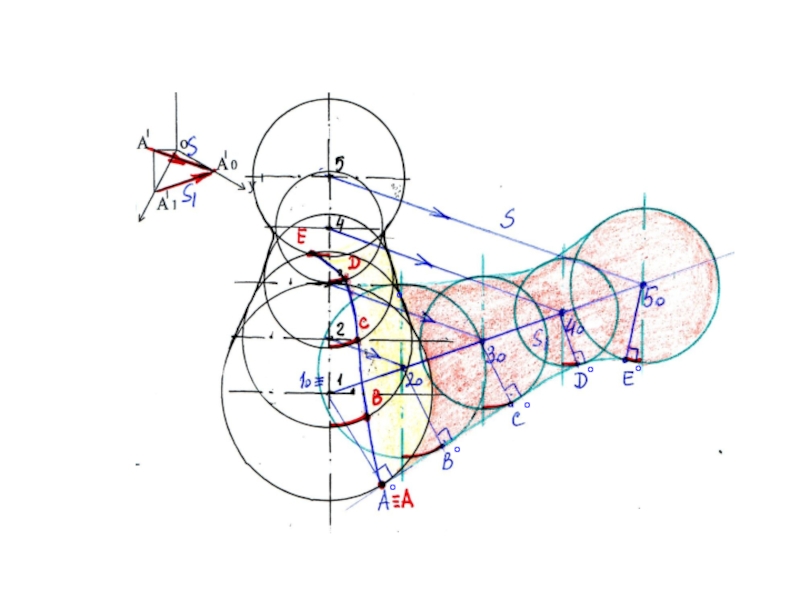
- 17. Задача 11.7 стр. 71: Построить горизонтальную изометрию, а также собственные и падающие тени поверхности вращения
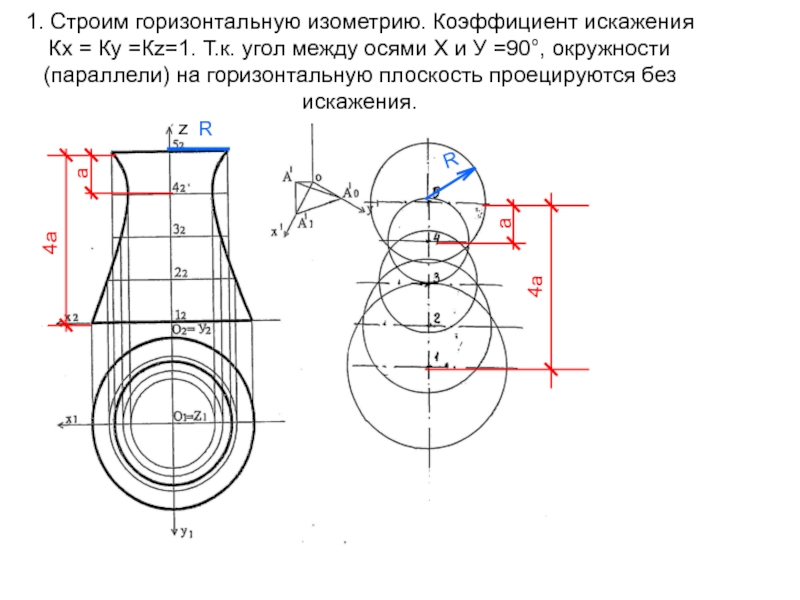
- 18. 1. Строим горизонтальную изометрию. Коэффициент искажения
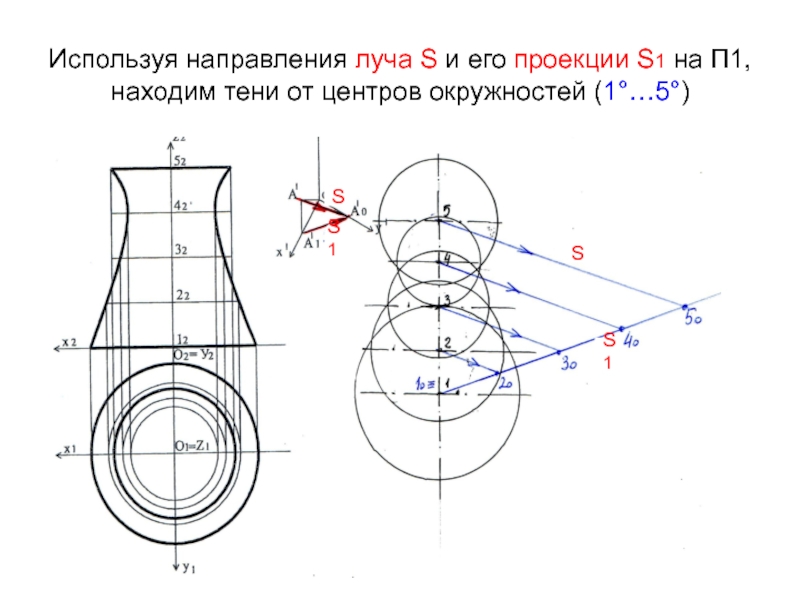
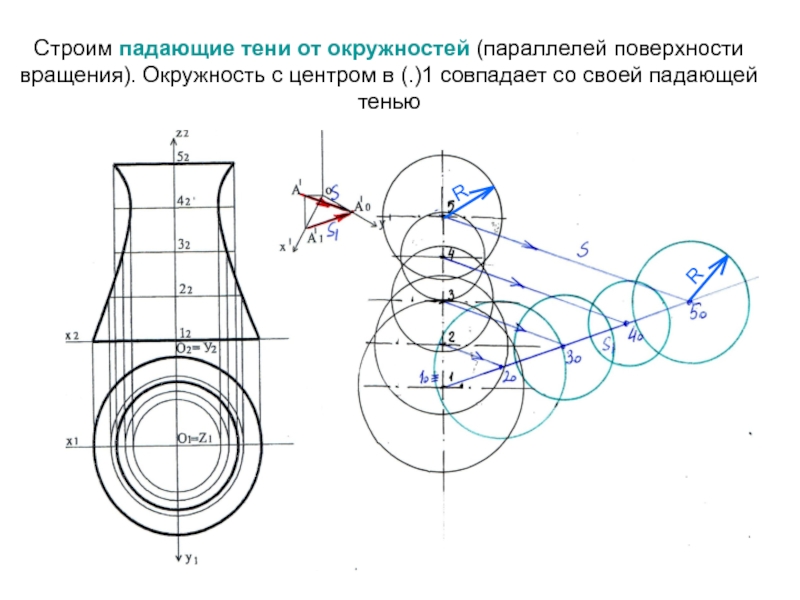
- 19. Используя направления луча S и его проекции S1 на П1, находим тени от центров окружностей (1°…5°)SS1SS1
- 20. Строим падающие тени от окружностей (параллелей поверхности
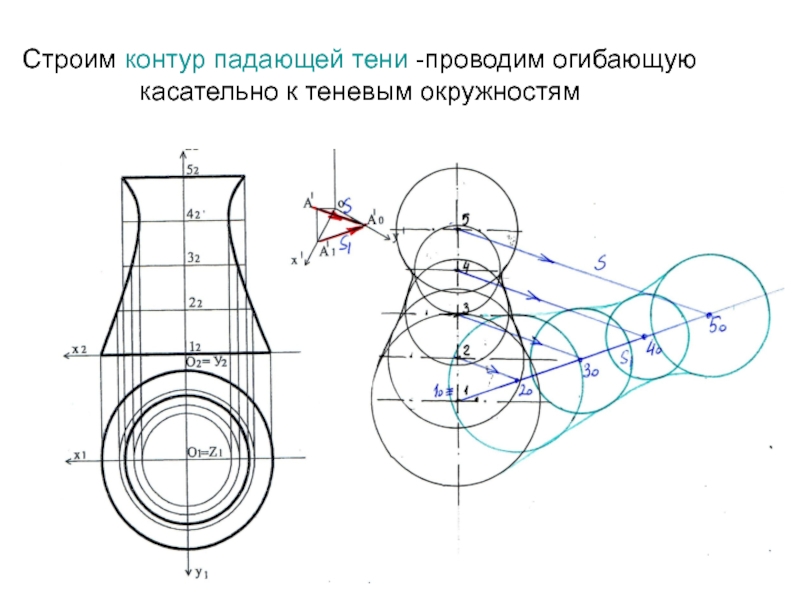
- 21. Строим контур падающей тени -проводим огибающую касательно к теневым окружностям
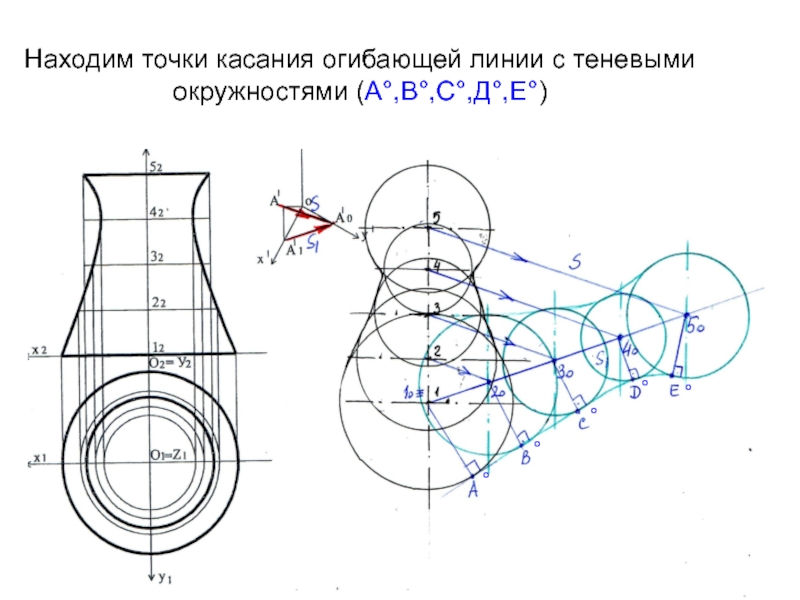
- 22. Находим точки касания огибающей линии с теневыми окружностями (А°,В°,С°,Д°,Е°)°°°°°
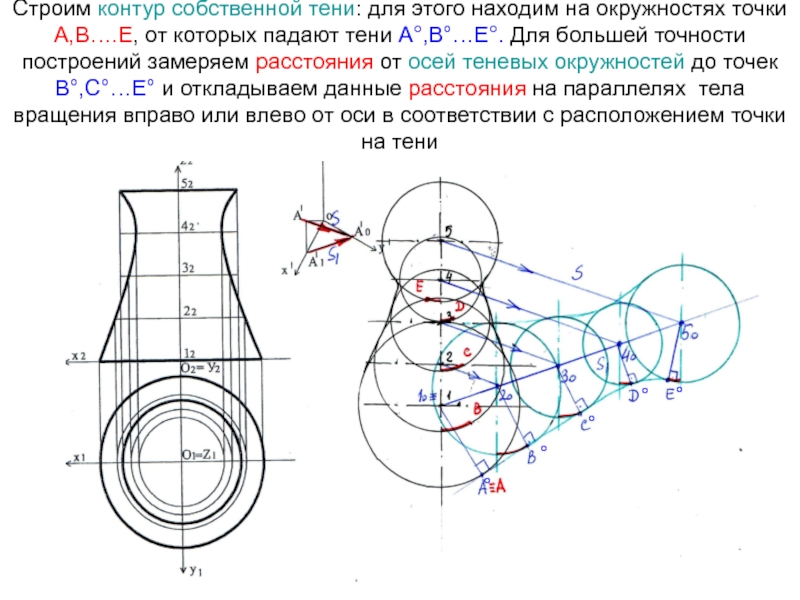
- 23. Строим контур собственной тени: для этого находим
- 24. °°°°°°
- 25. Построение падающих и собственных теней тела вращения
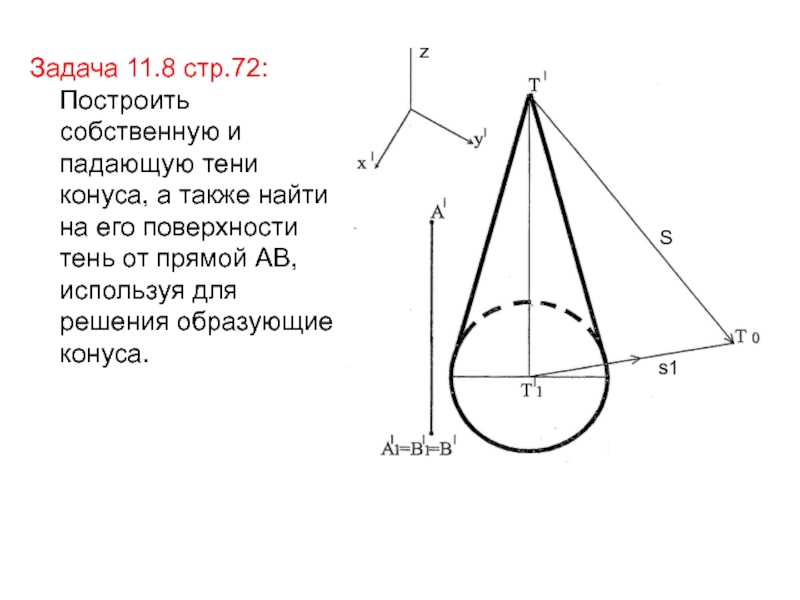
- 26. Задача 11.8 стр.72: Построить собственную и падающую
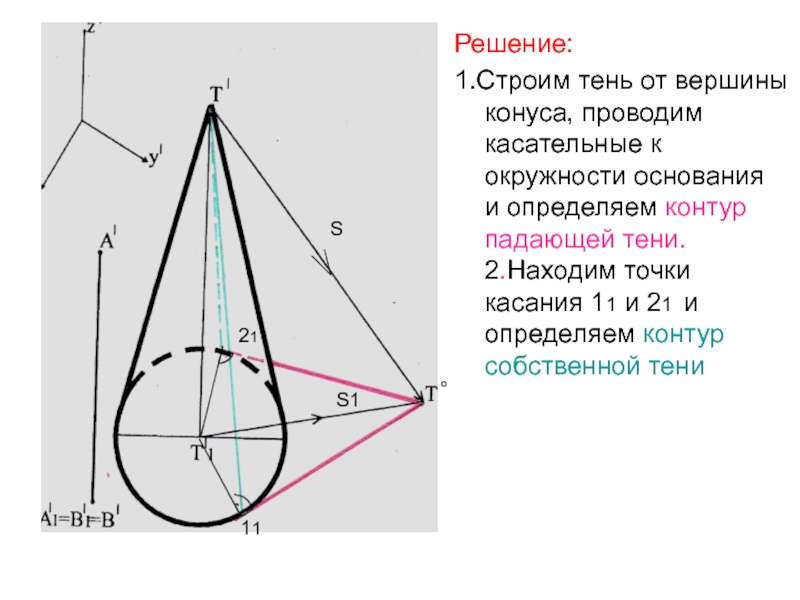
- 27. Решение: 1.Строим тень от вершины конуса, проводим
- 28. 3.Строим падающую тень от прямой АВ, как
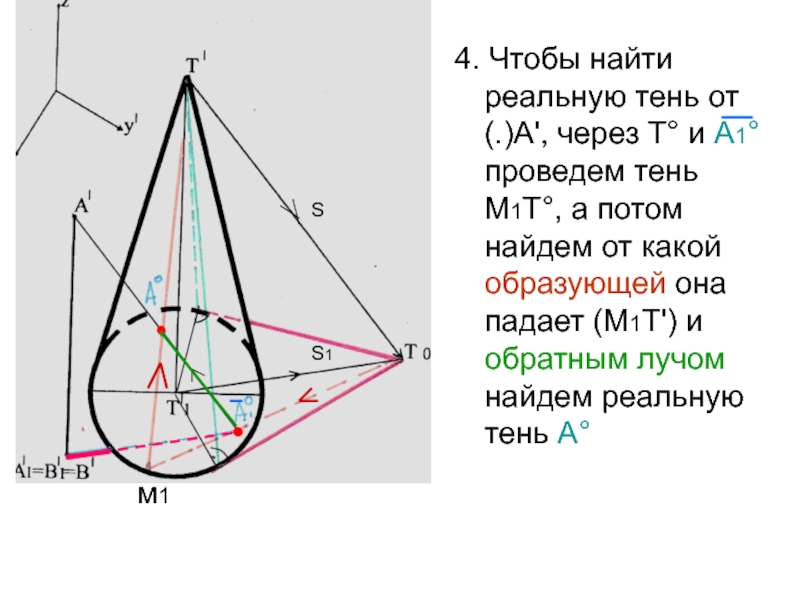
- 29. 4. Чтобы найти реальную тень от (.)А',
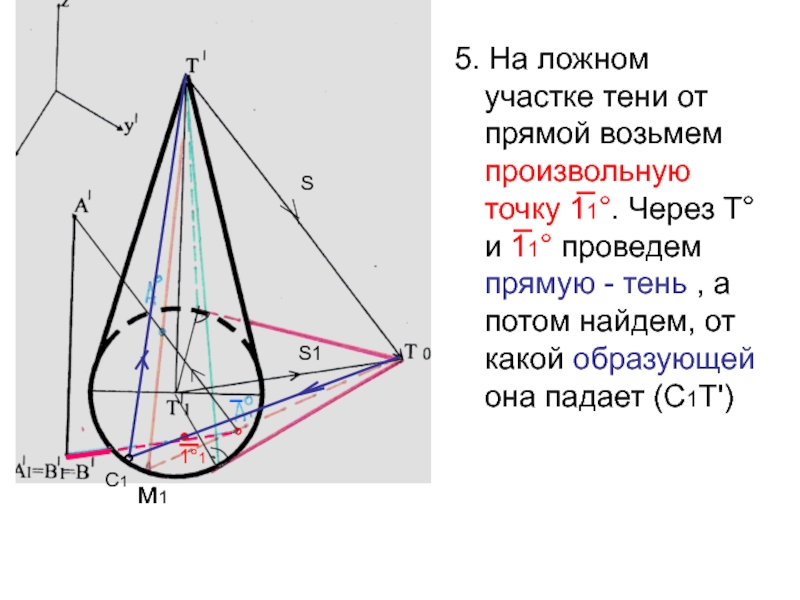
- 30. 5. На ложном участке тени от прямой
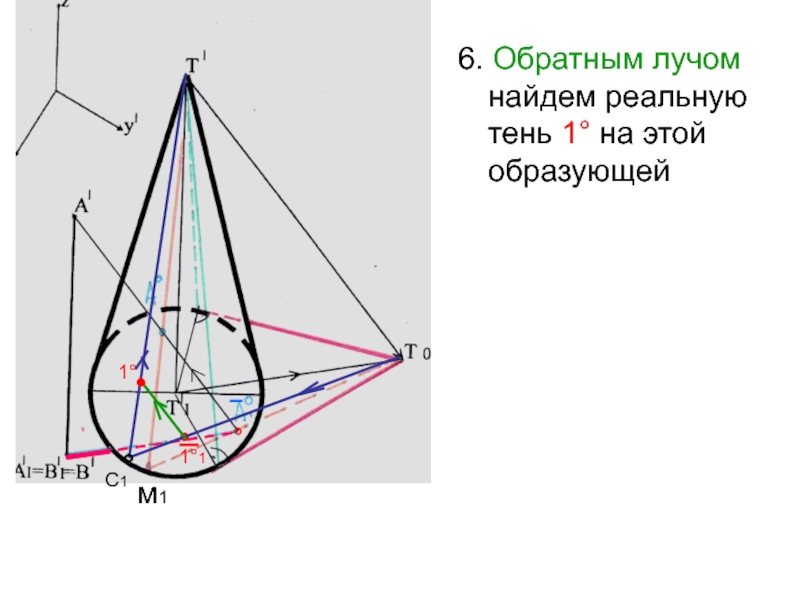
- 31. 6. Обратным лучом найдем реальную тень 1° на этой образующейм1с1°●1°1C1°●1°
- 32. 7. Соединим найденные точки- получим тень от
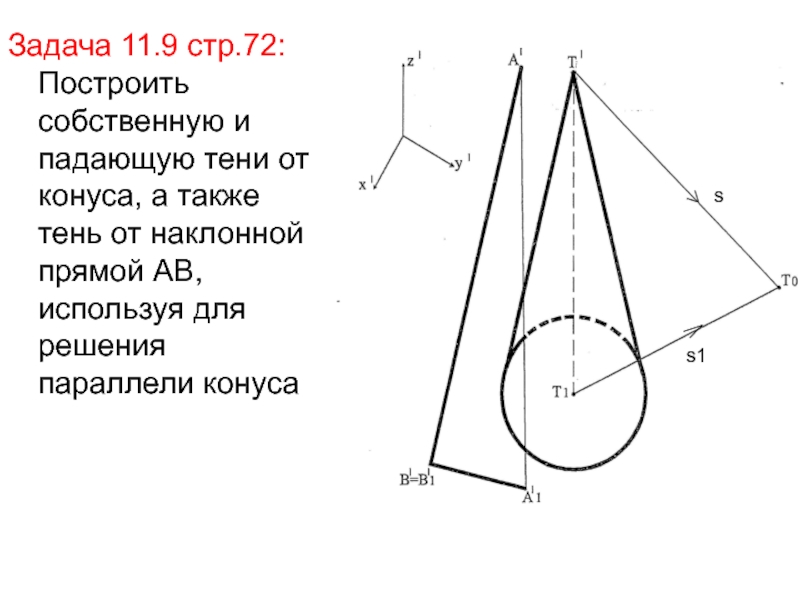
- 33. Задача 11.9 стр.72: Построить собственную и падающую
- 34. Решение:1). Находим собственные и падающие тени конуса.
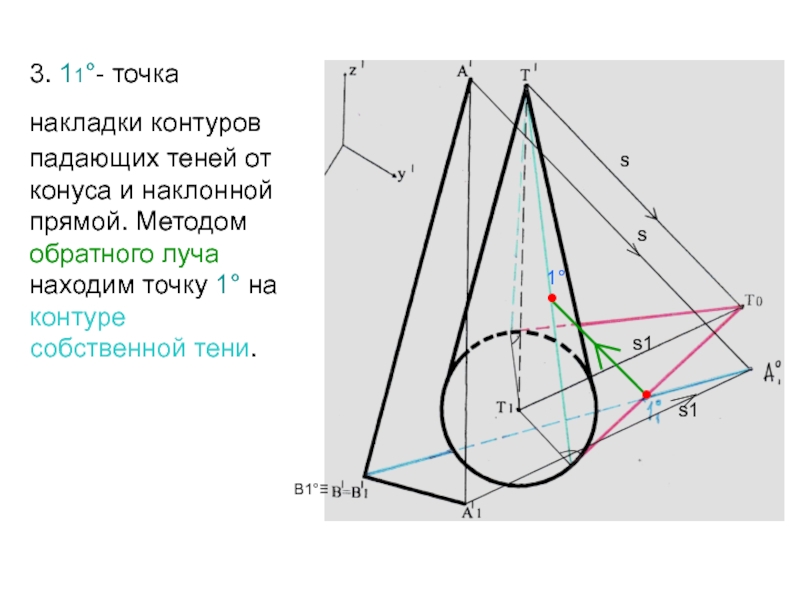
- 35. 3. 11°- точка накладки контуров падающих теней
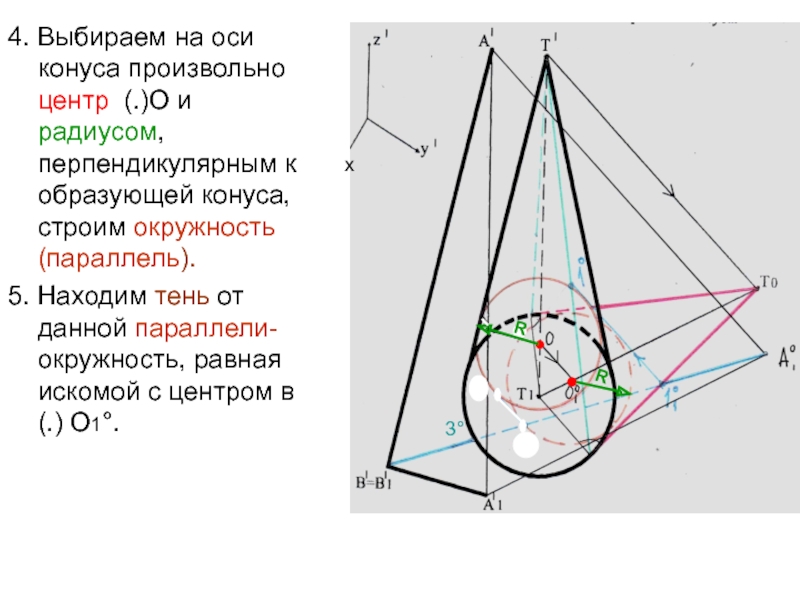
- 36. 4. Выбираем на оси конуса произвольно центр
- 37. 6. Определяем накладку контуров падающих теней (.)21°
- 38. 7.Завершаем построение падающей тени от наклонной прямой
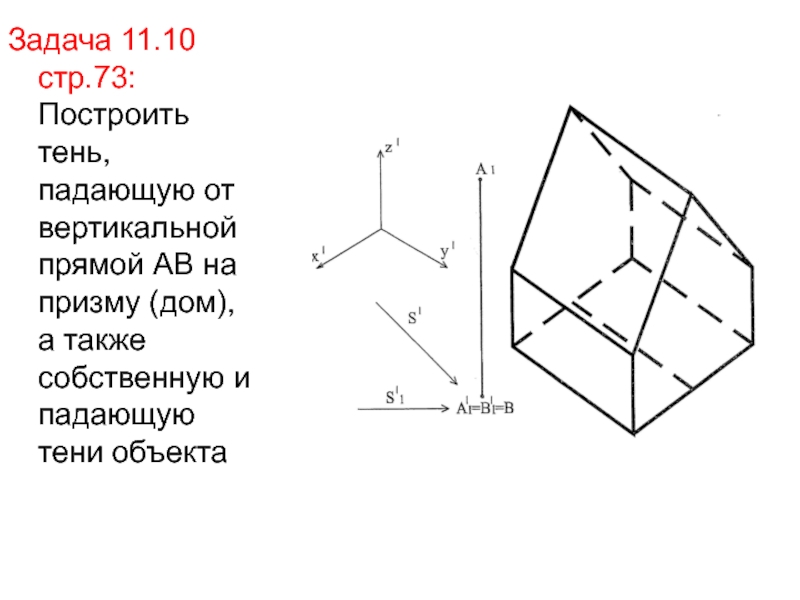
- 39. Задача 11.10 стр.73: Построить тень, падающую от
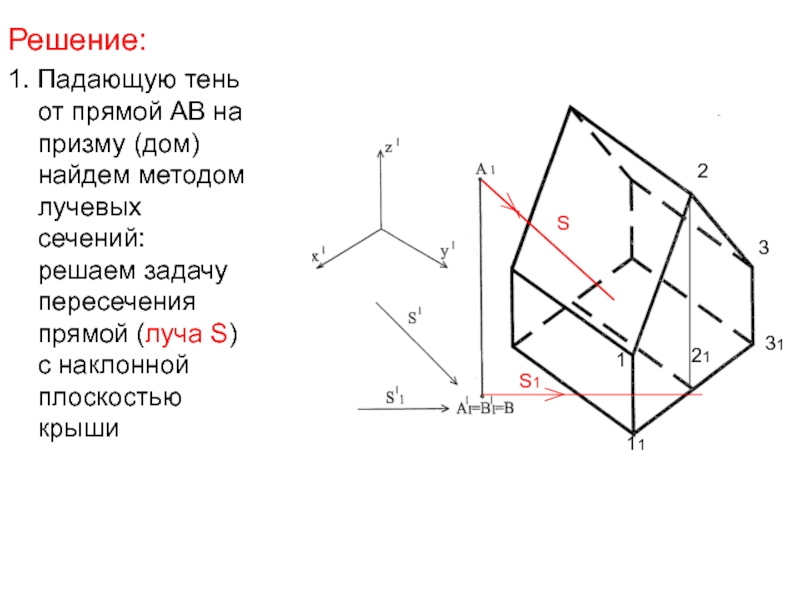
- 40. Решение:1. Падающую тень от прямой АВ на
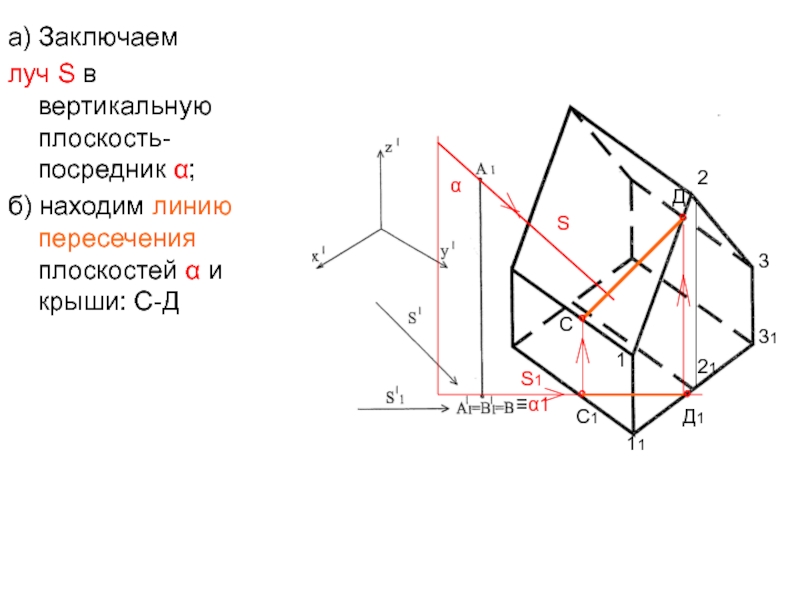
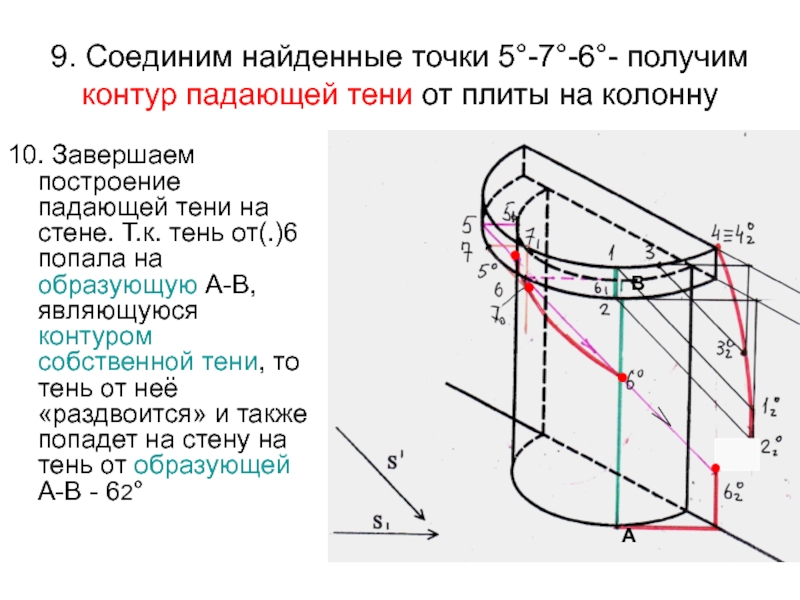
- 41. а) Заключаем луч S в вертикальную плоскость-посредник
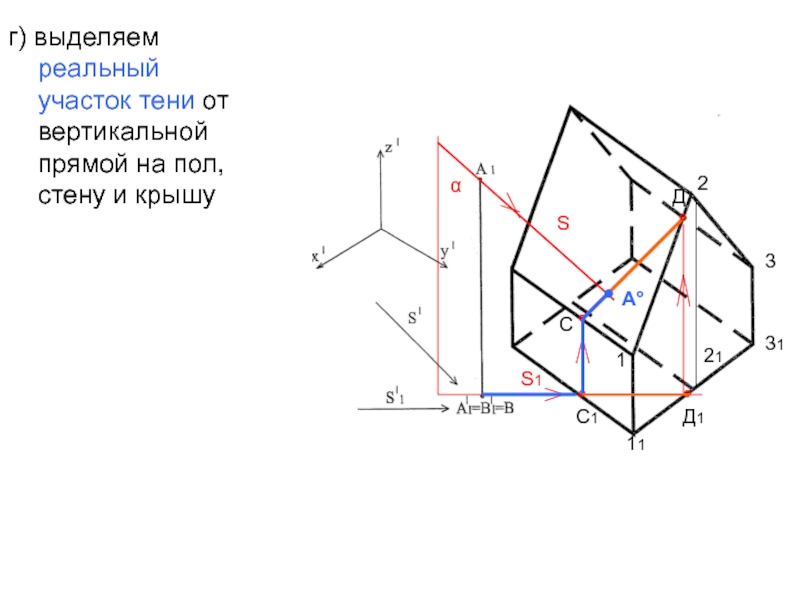
- 42. в) Находим пересечение луча S с линией пересечения двух плоскостей:S ∩ СД= А°SS1111221αС1Д1°°СД°°●А°
- 43. г) выделяем реальный участок тени от вертикальной прямой на пол, стену и крышу SS1111221αС1Д1°°СД°°●А°331
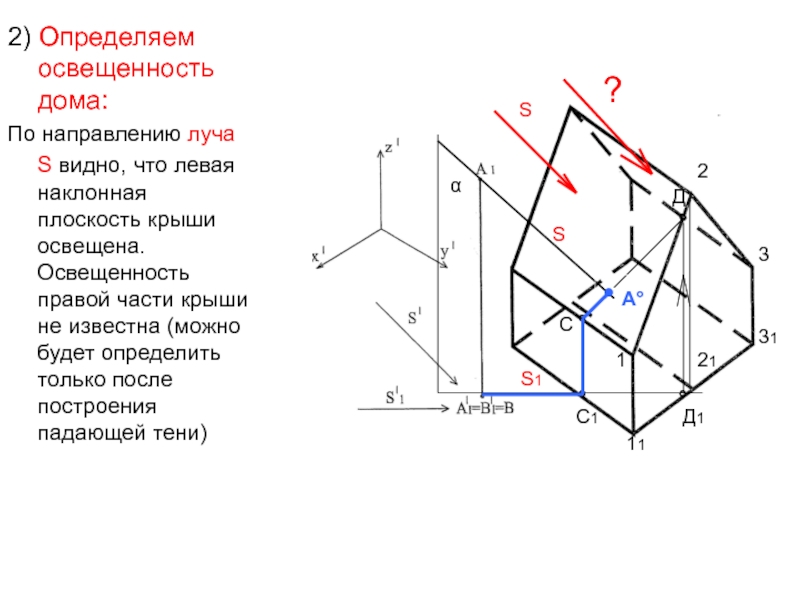
- 44. 2) Определяем освещенность дома: По направлению луча
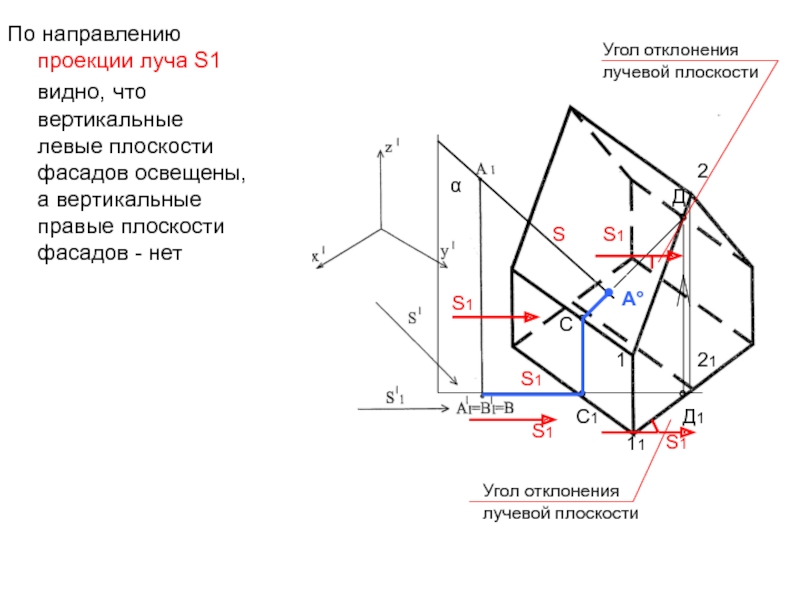
- 45. По направлению проекции луча S1 видно, что
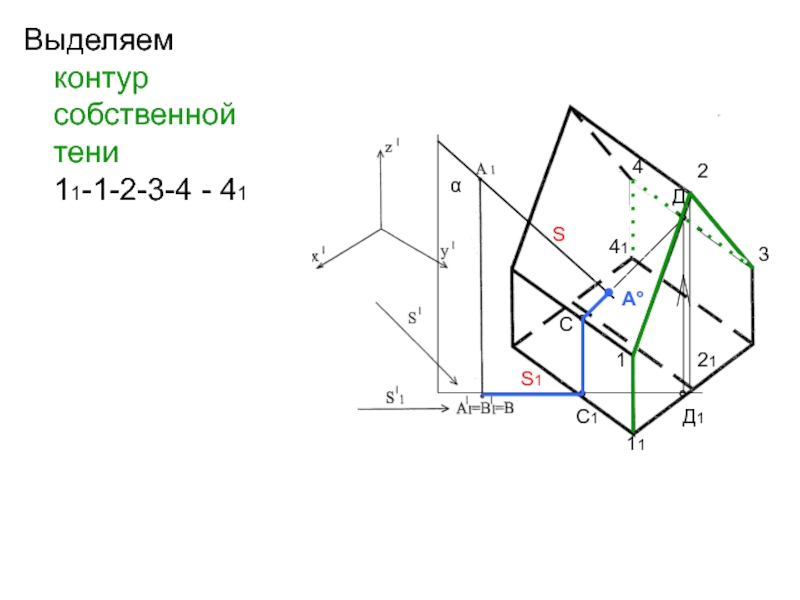
- 46. Выделяем контур собственной тени 11-1-2-3-4 - 41SS1111221αС1Д1°°СД°°●А°3441
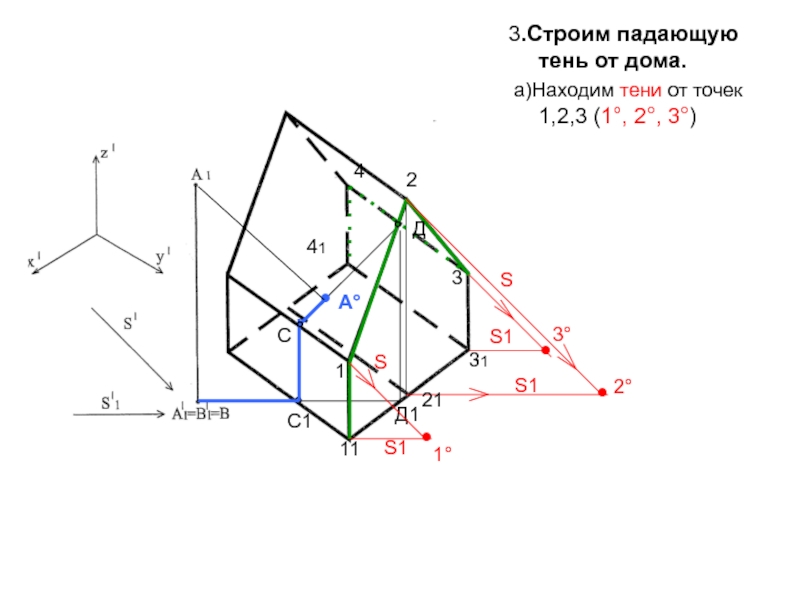
- 47. 3.Строим падающую тень от дома. а)Находим тени от точек 1,2,3 (1°, 2°, 3°)°41С1С4Д°А°●21111°Д12S1S1●3°331●2°S1●1°SS
- 48. б) Соединив найденные точки, найдем контур падающей тени от торцевой плоскости 11-1-2-3-31°41С1С4Д°А°●21111°Д12S1S1●3°331●2°S1●1°SS
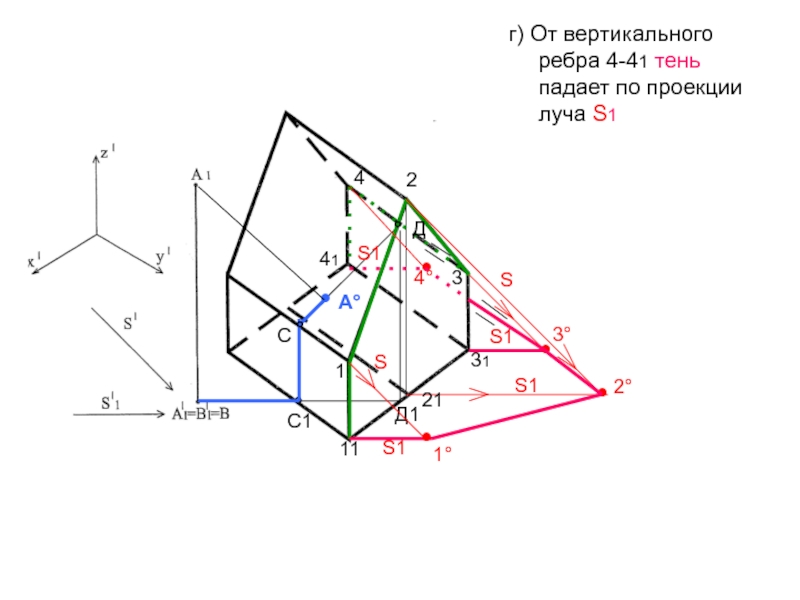
- 49. в) Строим падающую тень от горизонтального ребра
- 50. г) От вертикального ребра 4-41 тень падает по проекции луча S1°41С1С4Д°А°●21111°Д12S1S1●3°331●2°S1●1°SS●4°S1
- 51. Строим тень от конька (горизонтального ребра 2-2*),
- 52. Построение теней на лестницеss1
- 53. Решение: 1. Определяем контур собственной тени
- 54. 3. Для нахождения тени от наклонной прямой
- 55. 4. Для нахождения тени на подступёнок применим
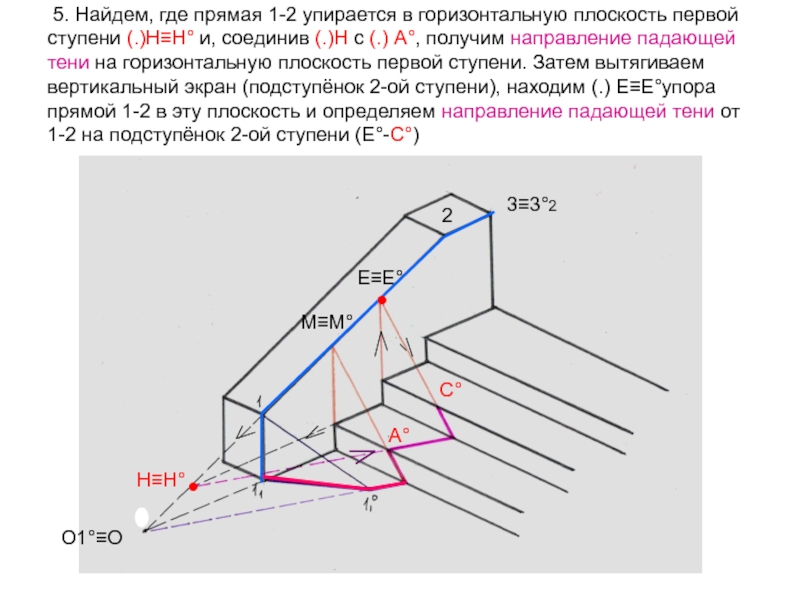
- 56. 5. Найдем, где прямая 1-2 упирается
- 57. 6. Повторяем операцию с 3-ей ступенью. Находим
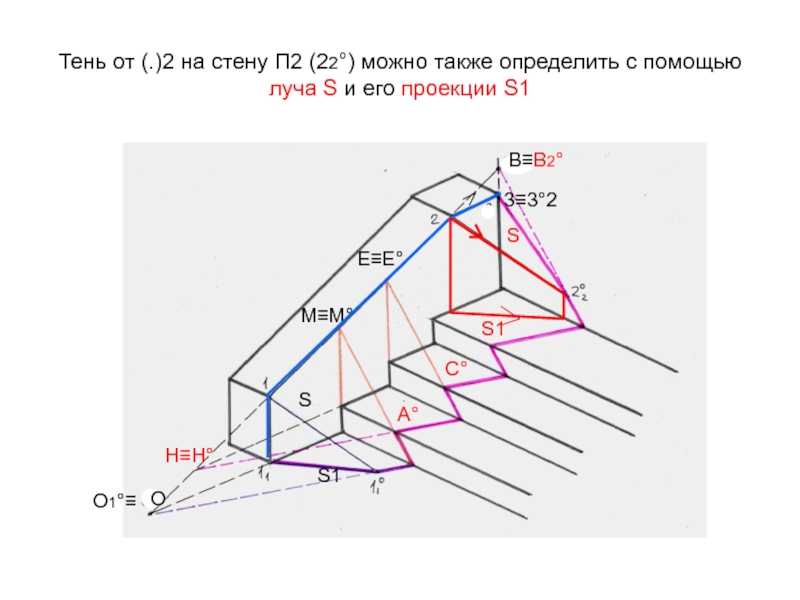
- 58. Тень от (.)2 на стену П2 (22°)
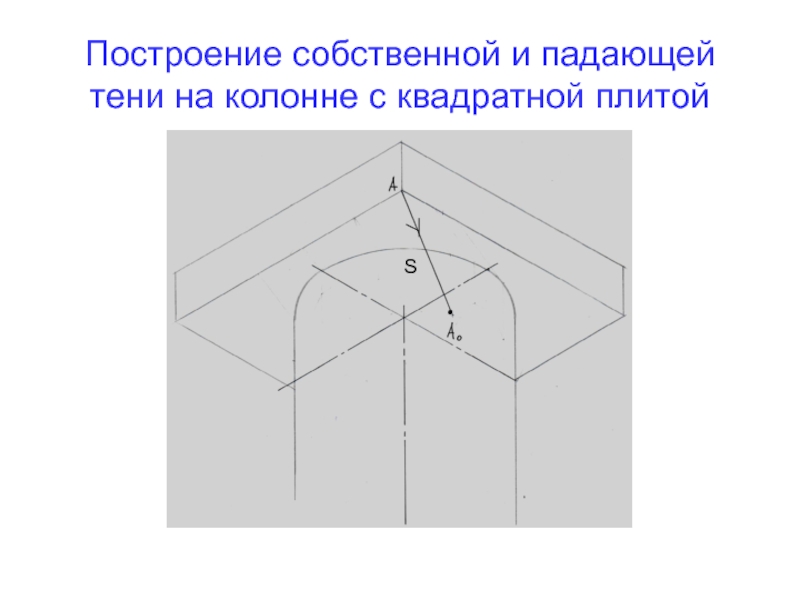
- 59. Построение собственной и падающей тени на колонне с квадратной плитойS
- 60. 1.Определяем контур собственной тени Определяем направление проекции
- 61. 2. Определение крайних точек видимого участка контура
- 62. 3. Определение наивысшей точки падающей тени от
- 63. 4. Построение теней от промежуточных точек Промежуточные точки Е, F выбираются произвольно.●В°●●D●●
- 64. 5.Соединяем найденные точки и получаем контур падающей тени от плиты на колонну
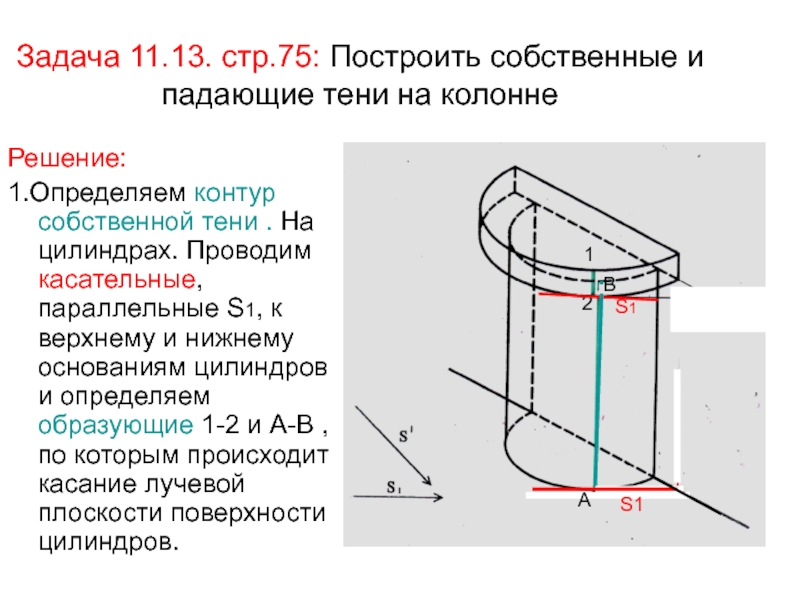
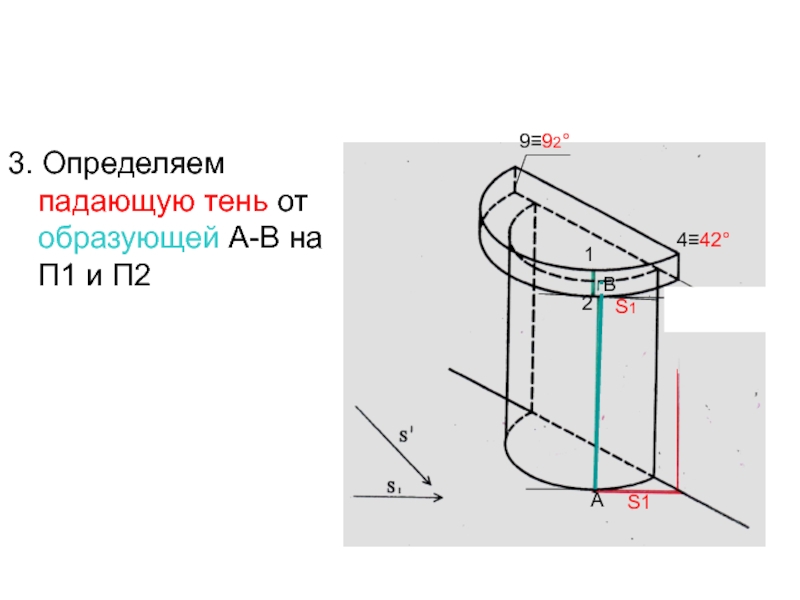
- 65. Задача 11.13. стр.75: Построить собственные и падающие
- 66. 2. По направлению луча S определяем, что
- 67. 3. Определяем падающую тень от образующей А-В на П1 и П2S112АВS14≡42°9≡92°
- 68. 4. Строим падающую тень от
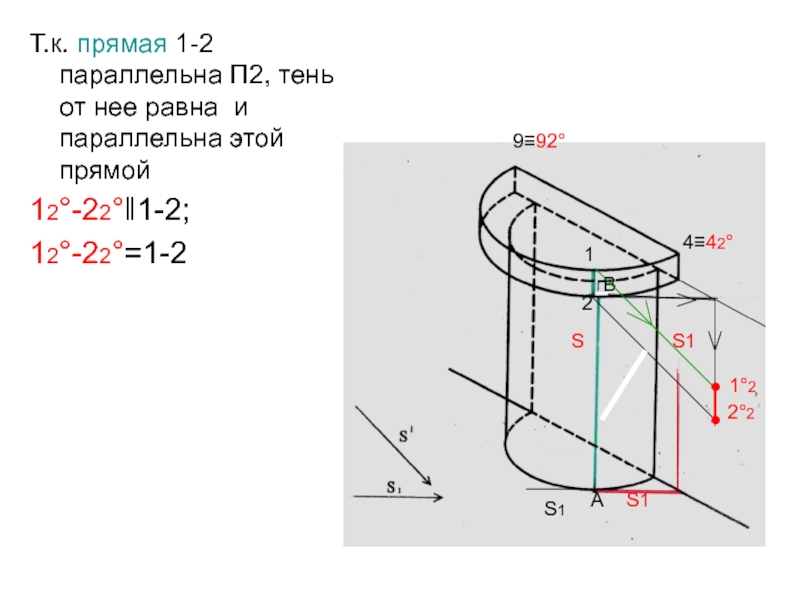
- 69. Т.к. прямая 1-2 параллельна П2, тень от нее равна и параллельна этой прямой12°-22°‖1-2; 12°-22°=1-2S112АВS1S●2°2●1°29≡92°4≡42°S1
- 70. 5. Строим тень от кривой 1-4.Произвольно на
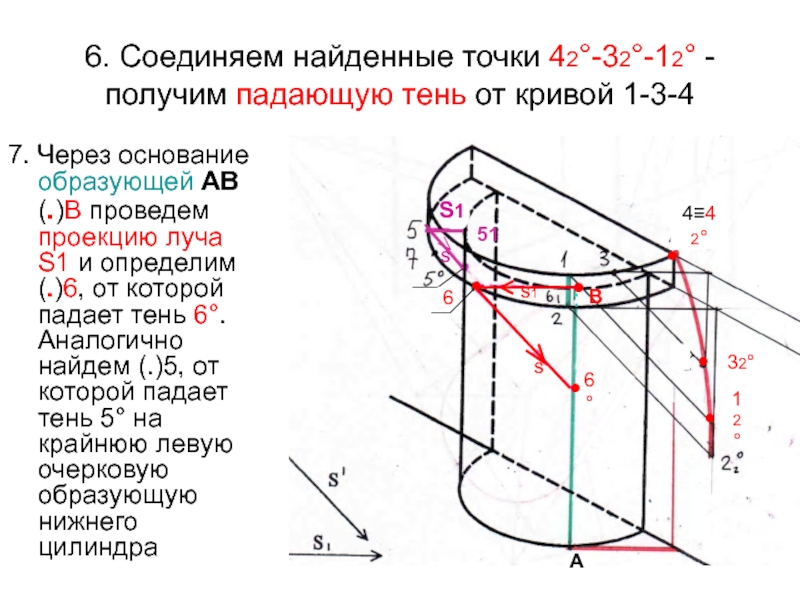
- 71. 6. Соединяем найденные точки 42°-32°-12° -получим падающую
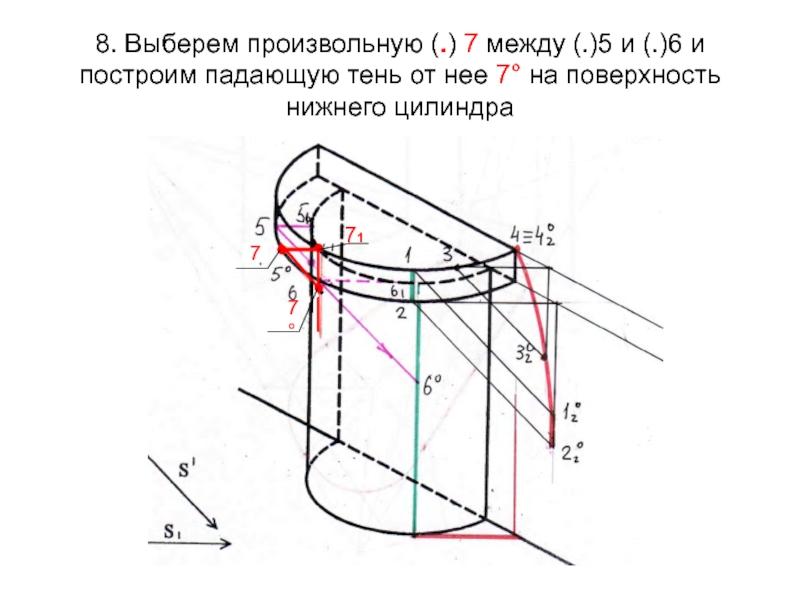
- 72. 8. Выберем произвольную (.) 7 между (.)5
- 73. 9. Соединим найденные точки 5°-7°-6°- получим контур
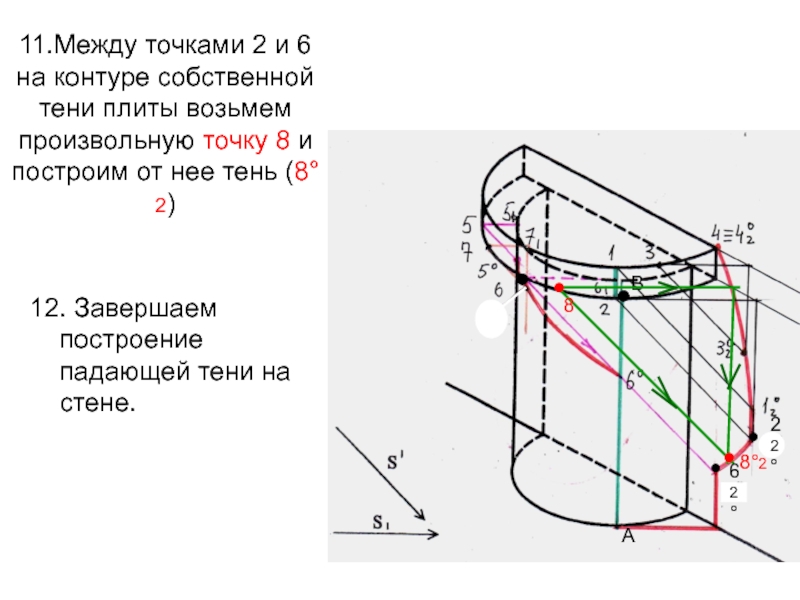
- 74. 11.Между точками 2 и 6 на контуре
- 75. Скачать презентанцию
Слайды и текст этой презентации
Слайд 1Лекция 13
Построение теней от геометрических тел
Построение теней на архитектурных деталях
Построение
теней на лестнице. Метод вспомогательных экранов
Слайд 2Способ вспомогательного проецирования
В этом способе используются дополнительные проекции светового луча
на плоскости П2 и П3.
Т.к. за направление светового луча
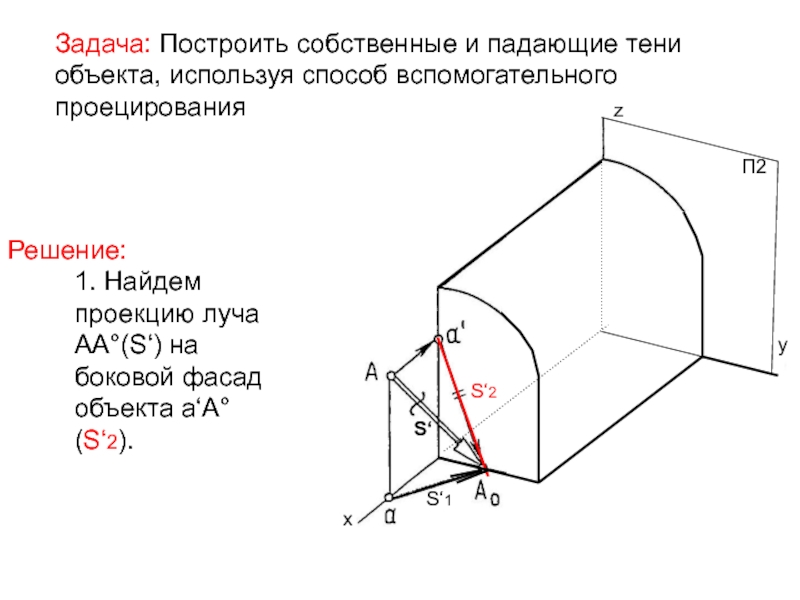
принята диагональ куба, всегда можно построить недостающие проекции луча, имея одну вторичную проекцию и луч SСлайд 3Решение: 1. Найдем проекцию луча АА°(S‘) на боковой фасад объекта
а‘А° (S‘2).
Е≡Е°2
М°2
S‘
S‘1
S‘2
●
y
z
x
Задача: Построить собственные и падающие тени объекта, используя
способ вспомогательного проецированияП2
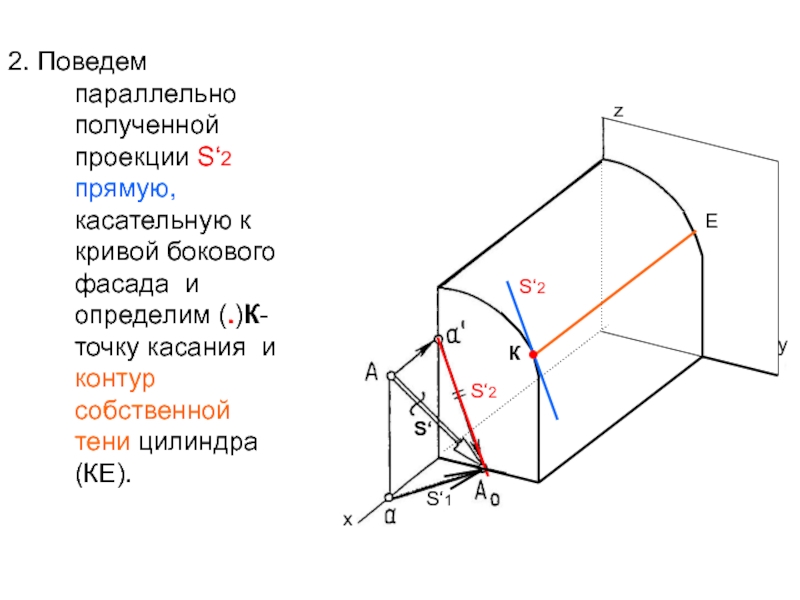
Слайд 42. Поведем параллельно полученной проекции S‘2 прямую, касательную к кривой
бокового фасада и определим (.)К- точку касания и контур собственной
тени цилиндра (КЕ).Е≡Е°2
М°2
S‘
S‘1
S‘2
●
y
z
x
●
К
Е
S‘2
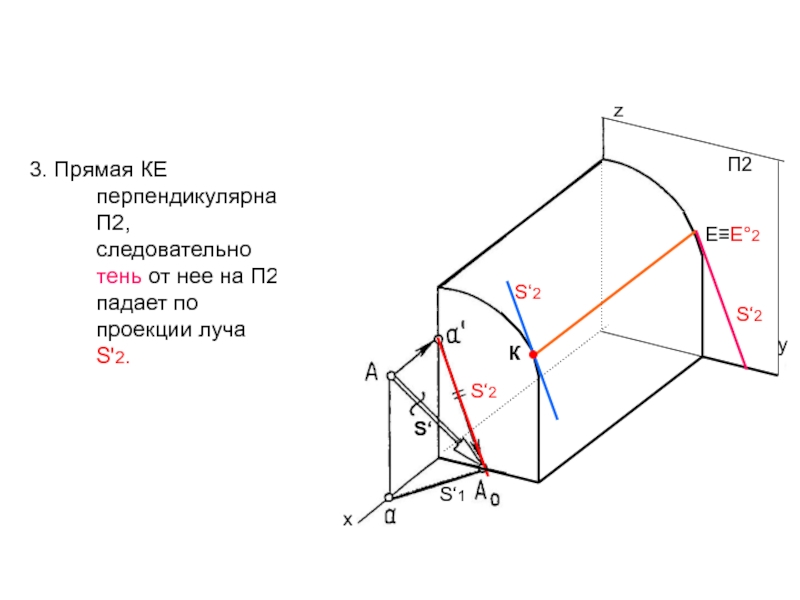
Слайд 53. Прямая КЕ перпендикулярна П2, следовательно тень от нее на
П2 падает по проекции луча S'2.
Е≡Е°2
М°2
S‘
S‘1
S‘2
●
y
z
x
●
К
Е≡Е°2
П2
S‘2
S‘2
Слайд 64. Прямая КЕ параллельна П1, следовательно тень от нее на
П1 параллельна самой прямой.
Е≡Е°2
М°2
S‘
S‘1
S‘2
●
y
z
x
●
К
Е≡Е°2
П2
S‘2
●
К°1
5. Проведем световой луч через (.)К и
найдем тень от неё (К°1)S
S‘2
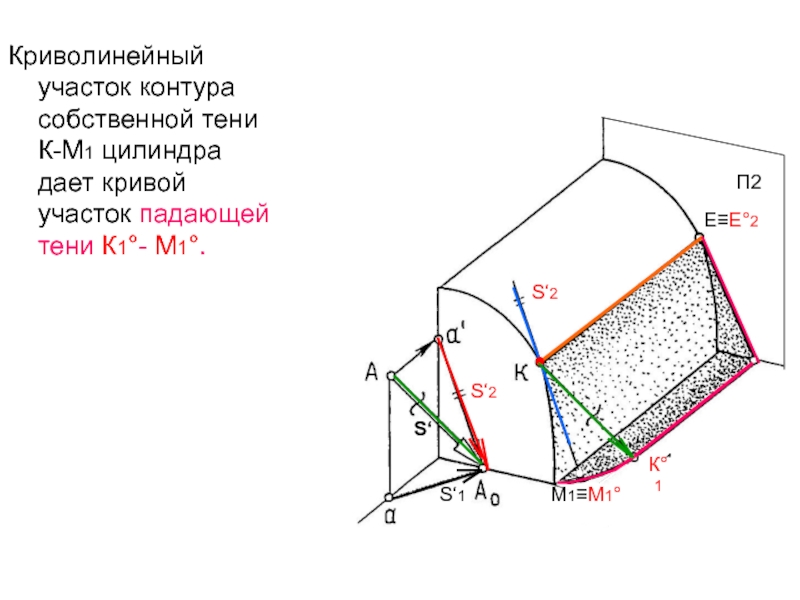
Слайд 7Криволинейный участок контура собственной тени К-М1 цилиндра дает кривой участок
падающей тени К1°- М1°.
Е≡Е°2
S‘
S‘1
S‘2
●
1°
К°1
П2
S‘2
M1≡M1°
Слайд 8Построение теней геометрического тела
Задача 11.5 стр.69: Построить собственные и падающие
тени двух призм при условии, что (.)А° является падающей тенью
от вершины призмыS
S1
Слайд 9Решение:
1. Определим собственные тени объекта (проекция луча S1 задает
направление лучевой плоскости, по которому видно, на какие грани попадает
свет.Т.к. луч S направлен сверху- горизонтальные плоскости освещены.
S
S1
S1
S1
S1
S1
S1
Слайд 10В собственной тени находятся правые боковые и задние плоскости. Контур
собственной тени нижней призмы: 11-1-А‘-2-21
Контур собственной тени верхней призмы: 31-3-4-5-6
S
S1
S1
S1
S1
S1
S1
Слайд 112. Находим падающие тени от нижнего объема:
(1-А‘= 1°-А°;
1-А‘
‖ 1°-А°;
2-А‘= 2°-А°;
2-А‘ ‖ 2°-А°
От вертикальных прямых контура
собственной тени 1-11 и 2-21 тени падают по направлению проекции луча на П1S1
S1
Слайд 12Строим падающую тень от верхней призмы. От вертикальной прямой 3-31
тень падает по направлению проекции луча на плоскость нижнего объема
призмы лишь частично. Находим реальный участок тени на П1, сделав срез лучевой плоскостью до П1 (вариант построения 1)S1
S
Слайд 13Вариант построения 2: срез лучевой плоскостью до П1 можно также
сделать, найдя проекцию вертикального ребра 3-31 на плоскость пола П1
(31)S1
S
●
31
Слайд 14Вариант построения 3: Реальный участок тени на П1 можно также
определить, используя правило, что от прямых, параллельных плоскости, тени на
эту плоскость равны и параллельны (1- В°= 1°1- В°1)S1
S
●
●
В°
В°1
11°
1
●
Слайд 15Прямые 3-4 и 4-5 параллельны П1, следовательно 3-4=3°- 4°; 3-4
‖3°-4°, 5-4=5°- 4°, 5-4 ‖ 5°-4°; от вертикального ребра 5
тень падает по направлению проекции луча1
Слайд 17Задача 11.7 стр. 71: Построить горизонтальную изометрию, а также собственные
и падающие тени поверхности вращения
Слайд 181. Строим горизонтальную изометрию. Коэффициент искажения Кх = Ку =Кz=1.
Т.к. угол между осями Х и У =90°, окружности (параллели)
на горизонтальную плоскость проецируются без искажения.R
R
z
a
a
4a
4a
Слайд 19Используя направления луча S и его проекции S1 на П1,
находим тени от центров окружностей (1°…5°)
S
S1
S
S1
Слайд 20Строим падающие тени от окружностей (параллелей поверхности вращения). Окружность с
центром в (.)1 совпадает со своей падающей тенью
R
R
Слайд 23Строим контур собственной тени: для этого находим на окружностях точки
А,В….Е, от которых падают тени А°,В°…Е°. Для большей точности построений
замеряем расстояния от осей теневых окружностей до точек В°,С°…Е° и откладываем данные расстояния на параллелях тела вращения вправо или влево от оси в соответствии с расположением точки на тени°
°
°
°
°
Слайд 25Построение падающих и собственных теней тела вращения Для построения тени
от наклонной прямой на тело вращения используем метод обратного луча.
Определяем
накладку падающей тени от наклонной прямой на теневые окружности и обратным лучом возвращаем точки накладки на окружности (параллели) тела вращения°
°
°
°
°
°
°
°
°
°
S
S1
Слайд 26Задача 11.8 стр.72: Построить собственную и падающую тени конуса, а
также найти на его поверхности тень от прямой АВ, используя
для решения образующие конуса.z
S
s1
Слайд 27Решение:
1.Строим тень от вершины конуса, проводим касательные к окружности
основания и определяем контур падающей тени. 2.Находим точки касания 11 и
21 и определяем контур собственной тени11
21
°
S1
S
Слайд 283.Строим падающую тень от прямой АВ, как будто конуса нет
Т.к.
произошла накладка падающих теней объектов, часть тени от прямой падает
не на П1, а на конус (т.е. под основанием конуса находится ложный участок тени от прямой АВ)х
11
21
S1
S
S
S1
А°1
●
Слайд 294. Чтобы найти реальную тень от (.)А', через Т° и
А1° проведем тень М1Т°, а потом найдем от какой образующей
она падает (М1Т') и обратным лучом найдем реальную тень А°м1
с1
●
●
S
S1
Слайд 305. На ложном участке тени от прямой возьмем произвольную точку
11°. Через Т° и 11° проведем прямую - тень ,
а потом найдем, от какой образующей она падает (С1Т')м1
с1
°
●
1°1
C1
°
S
S1
Слайд 327. Соединим найденные точки- получим тень от вертикальной прямой на
конус. Тень падает по кривой - гиперболе
м1
с1
х
°
1°
●
●
●
Слайд 33Задача 11.9 стр.72: Построить собственную и падающую тени от конуса,
а также тень от наклонной прямой АВ, используя для решения
параллели конусаs
s1
Слайд 34Решение:1). Находим собственные и падающие тени конуса. 2). Строим тень от
наклонной прямой, как будто конуса нет.
Точка В' ≡В1'≡В1°
1)
s
s1
11
21
s
s1
В1°≡
2)
s
s1
Слайд 353. 11°- точка накладки контуров падающих теней от конуса и
наклонной прямой. Методом обратного луча находим точку 1° на контуре
собственной тени.s
s1
В1°≡
s
s1
●
●
1°
Слайд 364. Выбираем на оси конуса произвольно центр (.)О и радиусом,
перпендикулярным к образующей конуса, строим окружность (параллель).
5. Находим тень
от данной параллели- окружность, равная искомой с центром в (.) О1°. х
3°
●
●
R
R
Слайд 376. Определяем накладку контуров падающих теней (.)21° и возвращаем ее
обратным лучом на окружность (параллель)→ 2°.
х
3°
°
●
●
●
Слайд 387.Завершаем построение падающей тени от наклонной прямой на конус, соединив
найденные точки 1°,2°,3°
х
3°
●
●
●
Слайд 39Задача 11.10 стр.73: Построить тень, падающую от вертикальной прямой АВ
на призму (дом), а также собственную и падающую тени объекта
Слайд 40Решение:
1. Падающую тень от прямой АВ на призму (дом) найдем
методом лучевых сечений: решаем задачу пересечения прямой (луча S) с
наклонной плоскостью крышиS
S1
1
11
2
21
3
31
Слайд 41а) Заключаем
луч S в вертикальную плоскость-посредник α;
б) находим линию
пересечения плоскостей α и крыши: С-Д
S
S1
1
11
2
21
α
С1
Д1
°
°
С
Д
°
°
≡α1
3
31
Слайд 42в) Находим пересечение
луча S с линией пересечения двух плоскостей:
S
∩ СД= А°
S
S1
1
11
2
21
α
С1
Д1
°
°
С
Д
°
°
●
А°
Слайд 43г) выделяем реальный участок тени от вертикальной прямой на пол,
стену и крышу
S
S1
1
11
2
21
α
С1
Д1
°
°
С
Д
°
°
●
А°
3
31
Слайд 442) Определяем освещенность дома:
По направлению луча S видно, что
левая наклонная плоскость крыши освещена. Освещенность правой части крыши не
известна (можно будет определить только после построения падающей тени)S
S1
1
11
2
21
α
С1
Д1
°
°
С
Д
°
°
●
А°
S
?
3
31
Слайд 45По направлению проекции луча S1 видно, что вертикальные левые плоскости
фасадов освещены, а вертикальные правые плоскости фасадов - нет
S
S1
1
11
2
21
α
С1
Д1
°
°
С
Д
°
°
●
А°
S1
S1
S1
Угол отклонения
лучевой
плоскостиУгол отклонения
лучевой плоскости
S1
Слайд 473.Строим падающую тень от дома.
а)Находим тени от точек
1,2,3 (1°, 2°, 3°)
°
41
С1
С
4
Д
°
А°
●
21
1
11
°
Д1
2
S1
S1
●
3°
3
31
●
2°
S1
●
1°
S
S
Слайд 48б) Соединив найденные точки, найдем контур падающей тени от торцевой
плоскости 11-1-2-3-31
°
41
С1
С
4
Д
°
А°
●
21
1
11
°
Д1
2
S1
S1
●
3°
3
31
●
2°
S1
●
1°
S
S
Слайд 49в) Строим падающую тень от горизонтального ребра 3-4:
3-4 ‖ П1
→ 3°- 4° ‖ 3- 4
3°- 4° = 3- 4°
41
С1
С
4
Д
°
А°
●
21
1
11
°
Д1
2
S1
S1
●
3°
3
31
●
2°
S1
●
1°
S
S
●
4°
Слайд 50г) От вертикального ребра 4-41 тень падает по проекции луча
S1
°
41
С1
С
4
Д
°
А°
●
21
1
11
°
Д1
2
S1
S1
●
3°
3
31
●
2°
S1
●
1°
S
S
●
4°
S1
Слайд 51Строим тень от конька (горизонтального ребра 2-2*), параллельного плоскости П1→
тень на П1 равна и параллельна
2-2*= 2°-2*°; 2-2*‖ 2°-2*°
°
41
С1
С
4
Д
°
А°
●
21
1
11
°
Д1
2
S1
S1
●
3°
3
31
●
2°
S1
●
1°
S
S
●
4°
S1
Т.к.тень
от горизонтального ребра 2-2* оказалась внутри тени от объекта, второй скат кровли тоже освещен. Контур собственной тени проходит по ребру 3-4 (как и предполагали ранее)2*
●
2*°
4) Проверяем, освещена ли вторая наклонная плоскость крыши.
Слайд 53 Решение: 1. Определяем контур собственной тени
(11-1-2-3)
s
s1
2.От вертикального ребра 1-11 тень падает по проекции луча s1
2
3≡3°2
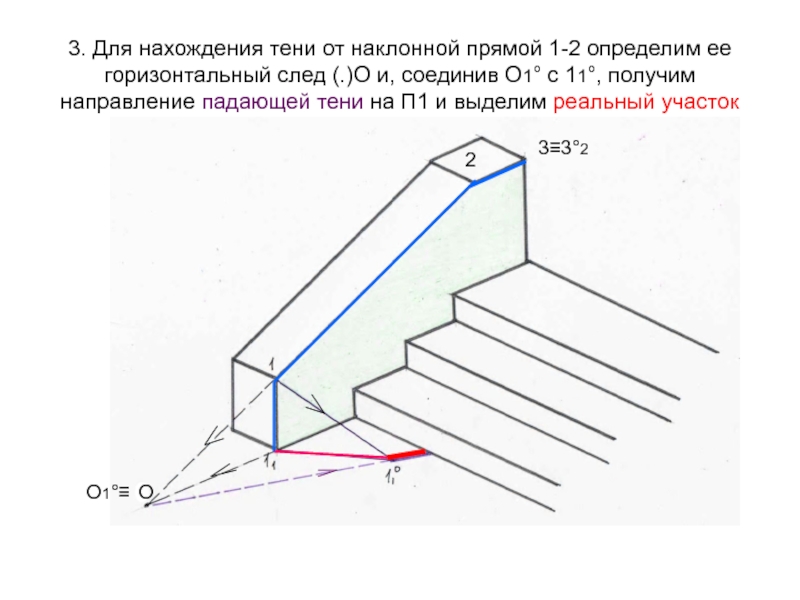
Слайд 543. Для нахождения тени от наклонной прямой 1-2 определим ее
горизонтальный след (.)О и, соединив О1° с 11°, получим направление
падающей тени на П1 и выделим реальный участок2
О1°≡
3≡3°2
О
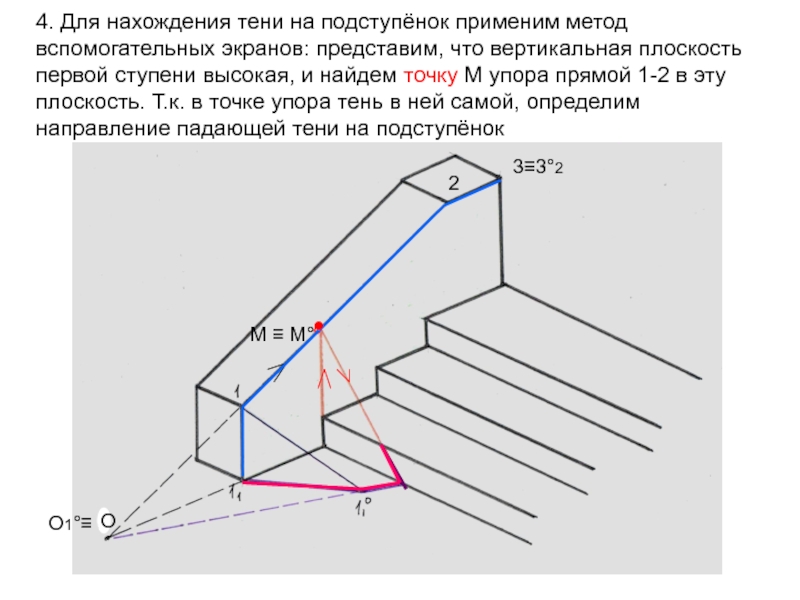
Слайд 554. Для нахождения тени на подступёнок применим метод вспомогательных экранов:
представим, что вертикальная плоскость первой ступени высокая, и найдем точку
М упора прямой 1-2 в эту плоскость. Т.к. в точке упора тень в ней самой, определим направление падающей тени на подступёнок2
О1°≡
°
М ≡ М°
3≡3°2
О
●
Слайд 56 5. Найдем, где прямая 1-2 упирается в горизонтальную плоскость
первой ступени (.)Н≡Н° и, соединив (.)Н с (.) А°, получим
направление падающей тени на горизонтальную плоскость первой ступени. Затем вытягиваем вертикальный экран (подступёнок 2-ой ступени), находим (.) Е≡Е°упора прямой 1-2 в эту плоскость и определяем направление падающей тени от 1-2 на подступёнок 2-ой ступени (Е°-С°)М≡М°
Н≡Н°
Е≡Е°
А°
2
С°
3≡3°2
О1°≡О
●
●
Слайд 576. Повторяем операцию с 3-ей ступенью. Находим тень от (.)2
на стену П2→ 22°(продлим прямую 1-2 до пересечения с П2-
тень в точке упора В2≡В2° в ней самой.) Далее строим тень от прямой 2-3: замыкаем в (.)3≡3°2(точка упора прямой 2-3 в плоскость П2)С°
А°
М≡М°
Е≡Е°
Н≡Н°
3≡3°2
О1°≡
О
В≡В2°
Слайд 58Тень от (.)2 на стену П2 (22°) можно также определить
с помощью луча S и его проекции S1
С°
А°
М≡М°
Е≡Е°
Н≡Н°
3≡3°2
2
О1°≡
S
S1
S
S1
О
В≡В2°
Слайд 601.Определяем контур собственной тени
Определяем направление проекции луча S1 :
через А° проводим вертикальную образующую и определяем её основание
(.)
А1. Соединяем (.)А и (.)А1По направлению светового луча S видно, что освещены верхняя плоскость плиты и передние боковые вертикальные грани. В собственной тени находятся нижняя плоскость плиты и задние вертикальные плоскости
Для определения контура собственной тени на цилиндре проводим касательную к основанию цилиндра параллельно S1 и определяем точку касания В1, через которую проходит контур собственной тени цилиндра
S1
S
Слайд 612. Определение крайних точек видимого участка контура падающей тени
Через
основание крайней левой образующей (.)С1 проводим проекцию луча S1 и
определяем (.)С, от которой падает тень С°Через (.)В проводим луч S и находим (.)В°
S
S1
●
S
S1
●
В°
С°
Слайд 623. Определение наивысшей точки падающей тени от плиты на колонну
D1 – точка пересечения
основания колонны с осью. Через (.)D1
проводим прямую, параллельную направлению проекции луча S1 и определяем (.) D , от которой строим падающую тень D° методом лучевого среза
S1
S
S
S1
S
S
В°
●
●
●
●
D
D1
D°
Слайд 634. Построение теней от промежуточных точек
Промежуточные точки Е, F выбираются
произвольно.
●
В°
●
●
D
●
●
Слайд 65Задача 11.13. стр.75: Построить собственные и падающие тени на колонне
Решение:
1.Определяем
контур собственной тени . На цилиндрах. Проводим касательные, параллельные S1,
к верхнему и нижнему основаниям цилиндров и определяем образующие 1-2 и А-В , по которым происходит касание лучевой плоскости поверхности цилиндров.S1
1
2
В
S1
А
Слайд 662. По направлению луча S определяем, что верхняя плоскость крыши
освещена, а нижняя нет. Контур собственной тени проходит по кривой
9…2, прямой 2-1 и кривой 1-4Т.о. в собственной тени находятся нижнее основание верхнего цилиндра и правые боковые поверхности цилиндров
S1
1
2
В
S1
S
4≡42°
А
9≡92°
Слайд 68
4. Строим падающую тень от образующей 1-2 на стену:
т.к. (.)2
принадлежит нижней плоскости верхнего цилиндра, она совпадает со своей проекцией
на эту плоскость. Проводим через (.) 2 луч S и проекцию луча S1. Определяем пересечение луча S с П2 → получим тень 2°2S1
S1
1
2
А
В
S1
S
●
2°2
4≡42°
9≡92°
Слайд 69Т.к. прямая 1-2 параллельна П2, тень от нее равна и
параллельна этой прямой
12°-22°‖1-2;
12°-22°=1-2
S1
1
2
А
В
S1
S
●
2°2
●
1°2
9≡92°
4≡42°
S1
Слайд 705. Строим тень от кривой 1-4.
Произвольно на контуре собственной тени
1-4 выбираем промежуточную точку 3 и строим тень 32° ,
используя линию врезки верхней плоскости крыши в П2S
●
3
9≡92°
4≡42°
●
32°
S1
S
А
В
Слайд 716. Соединяем найденные точки 42°-32°-12° -получим падающую тень от кривой
1-3-4
7. Через основание образующей АВ (.)В проведем проекцию луча
S1 и определим (.)6, от которой падает тень 6°. Аналогично найдем (.)5, от которой падает тень 5° на крайнюю левую очерковую образующую нижнего цилиндраs1
s
А
s
●
4≡42°
32°
●
●
●
12°
В
●
6
6°
●
S1
51
Слайд 728. Выберем произвольную (.) 7 между (.)5 и (.)6 и
построим падающую тень от нее 7° на поверхность нижнего цилиндра
●
7
●
71
7°
●
Слайд 739. Соединим найденные точки 5°-7°-6°- получим контур падающей тени от
плиты на колонну
10. Завершаем построение падающей тени на стене. Т.к.
тень от(.)6 попала на образующую А-В, являющуюся контуром собственной тени, то тень от неё «раздвоится» и также попадет на стену на тень от образующей А-В - 62°В
А
●
●
●
●
Слайд 7411.Между точками 2 и 6 на контуре собственной тени плиты
возьмем произвольную точку 8 и построим от нее тень (8°2)
12.
Завершаем построение падающей тени на стене. В
А
●
●
8
8°2
●
●
62°
●
●
22°