Слайд 1
Лекция 11. Временные параллельные алгоритмы.
Тема 3. Методы параллельной
обработки данных
1.
Определение и понятие временных
параллельных алгоритмов.
2. Временные Параллельные Граф-Схемы-
способ визуализации
временных
параллельных алгоритмов.
Слайд 2Первый вопрос. Определение и понятие
временных параллельных алгоритмов .
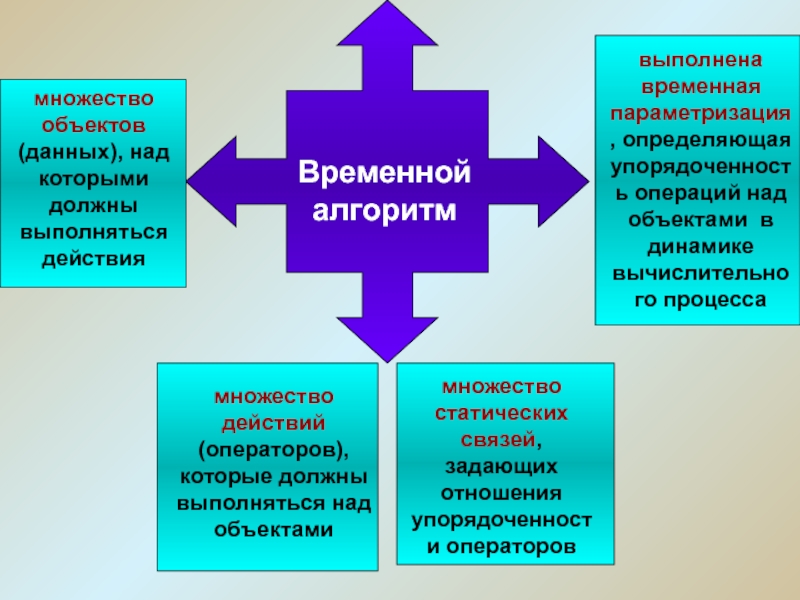
Временной алгоритм
Параметр
начала
Временная глубина
Интервал активности операторов
Слайд 3Алгоритм – конечная “последовательность общепринятых предписаний, формальное, не требующее проявления
человеческой изобретательности, исполнение которых позволяет за конечное время получить решение
некоторой задачи или любой задачи из некоторого класса задач”;
алгоритм - это “четкое предписание, определяющее вычислительный процесс, которое, исходя из вводных данных, приводит к решению поставленной задачи;
алгоритм - “совокупность правил, задающих эффективную процедуру решения любой задачи из заданного класса задач”.
Содержательные определения алгоритма
Слайд 4Конструктивное определение алгоритма.
Примем, что алгоритм – это формальная математическая
система, описывающая решение задачи или класса задач, которая характеризуется следующими
статическими категориями данных:
а) множеством объектов / данных (D, Data), над которыми должны выполняться те или иные действия;
б) множеством действий /операторов (Р, Processing), которые должны выполняться над объектами/данными;
в) множеством статических связей (C, Communication), задающих отношения упорядоченности операторов по данным и по управлению.
Слайд 5
Будем называть алгоритм статическим, если его реализация включает выполнение
функциональных, управляющих и пространственных преобразований и не включает временные преобразования.
Используем для статических алгоритмов следующее формальное обозначение S_A = (D, Р, C ) (S_A, Static Algorithm).
Алгоритм, содержащий в числе выполняемых преобразований временные преобразования, будем называть временным алгоритмом. Используем для временных алгоритмов следующее формальное обозначение Т_A = ( D, P, C , T) (Т_A, Timing Algorithm), где Т - множество временных параметров, определяющих моменты начала выполнения действий (операторов) над объектами и их длительность.
Слайд 6Сопряженное множество оператора. Обозначим через
Sj =S( Pj ) множество номеров операторов Pi ,
результаты выполнения которых использует Pj при своей реализации. Назовем Sj сопряженным множеством для Pj .Операторы Pi , для которых i Wj , являются сопряженными для Рj .
Внешнее множество оператора. Пусть Рj - оператор функционального, временного, пространственного преобразования или безусловный управляющий оператор, Wj - множество номеров операторов Рi , каждый из которых использует при своей реализации результаты выполнения оператора Рj . Назовем Wj внешним множеством для функционального, временного, пространственного или безусловного управляющего оператора Рj . Операторы Рi , для которых i Wj , являются внешними для Рj .
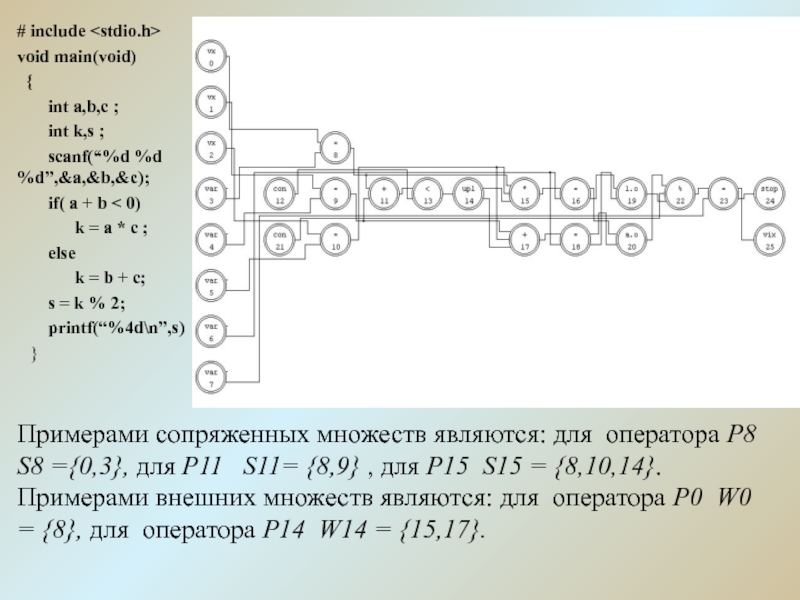
Слайд 7# include
void main(void)
{
int
a,b,c ;
int k,s ;
scanf(“%d %d %d”,&a,&b,&c);
if( a + b < 0)
k = a * c ;
else
k = b + c;
s = k % 2;
printf(“%4d\n”,s)
}
Примерами сопряженных множеств являются: для оператора Р8 S8 ={0,3}, для Р11 S11= {8,9} , для Р15 S15 = {8,10,14}. Примерами внешних множеств являются: для оператора Р0 W0 = {8}, для оператора Р14 W14 = {15,17}.
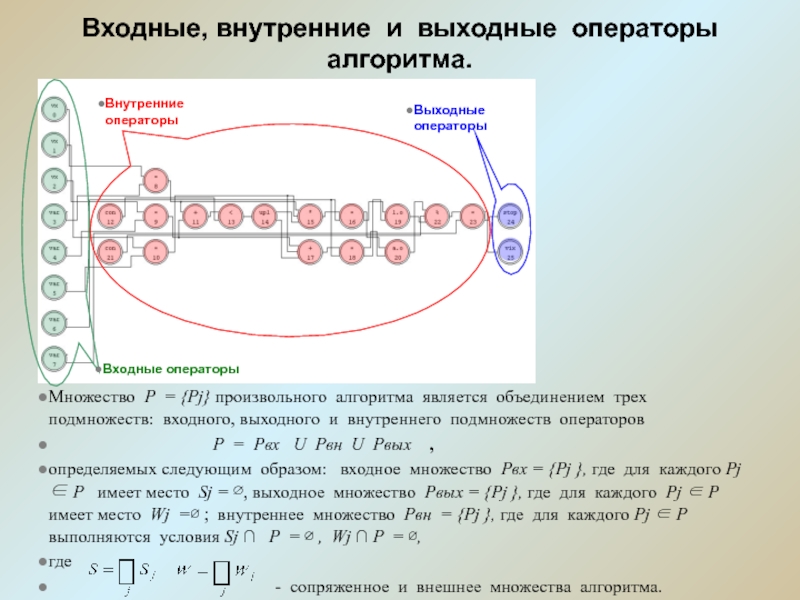
Слайд 8Входные, внутренние и выходные операторы алгоритма.
Множество Р = {Рj} произвольного
алгоритма является объединением трех подмножеств: входного, выходного и внутреннего подмножеств
операторов
Р = Рвх U Рвн U Рвых ,
определяемых следующим образом: входное множество Рвх = {Рj }, где для каждого Рj Р имеет место Sj = , выходное множество Рвых = {Рj }, где для каждого Рj Р имеет место Wj = ; внутреннее множество Рвн = {Рj }, где для каждого Рj Р выполняются условия Sj P = , Wj P = ,
где
- сопряженное и внешнее множества алгоритма.
Слайд 9Статический алгоритм
Алгоритм будем называть статическим (S_A), если для него
определены:
а) множество объектов (данных), над которыми должны выполняться действия;
б) множество действий (операторов), которые преобразуют входные данные операторов в выходные данные (результаты);
в) множество статических связей, задающих отношения упорядоченности операторов по данным и по управлению в форме сопряженных и внешних множеств.
В качестве формальной записи статического алгоритма будем использовать
форму S_A = ( D , Р , S ,W ), в которой D - подмножество операторов - данных (формально трактуемых далее как «невыполняемые» операторы); Р = {Pj}, (j= 0,1,2,...,p) - подмножество «выполняемых» операторов, S - сопряженное и W - внешнее множества для алгоритма S_A.
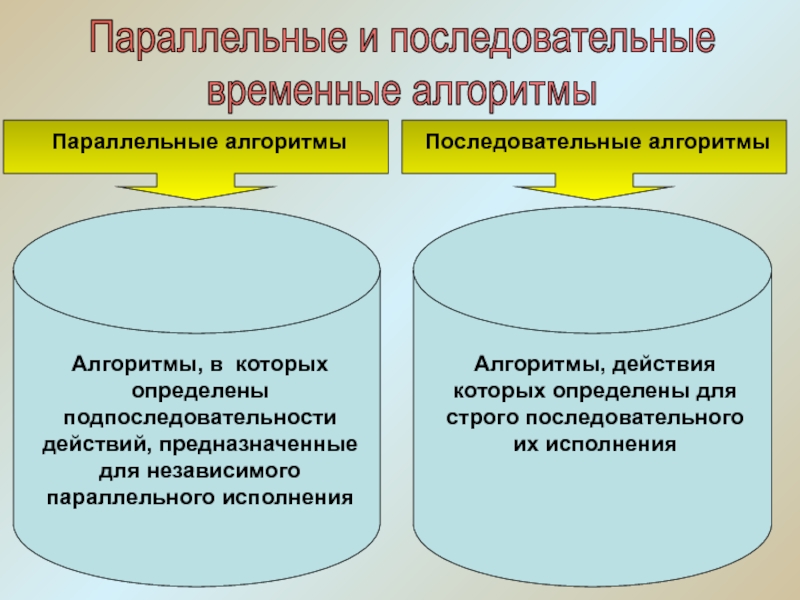
Слайд 10Параллельные и последовательные
временные алгоритмы
Слайд 12# include
# include
void main(void)
{
double x,y,z;
double z1,z2 ;
scanf(“%e% 5e\n”,
&x,&y) ;
z1=sin(x);
z2=cos(y);
z=z1+z2 ;
printf(“%e\n”,z);
}
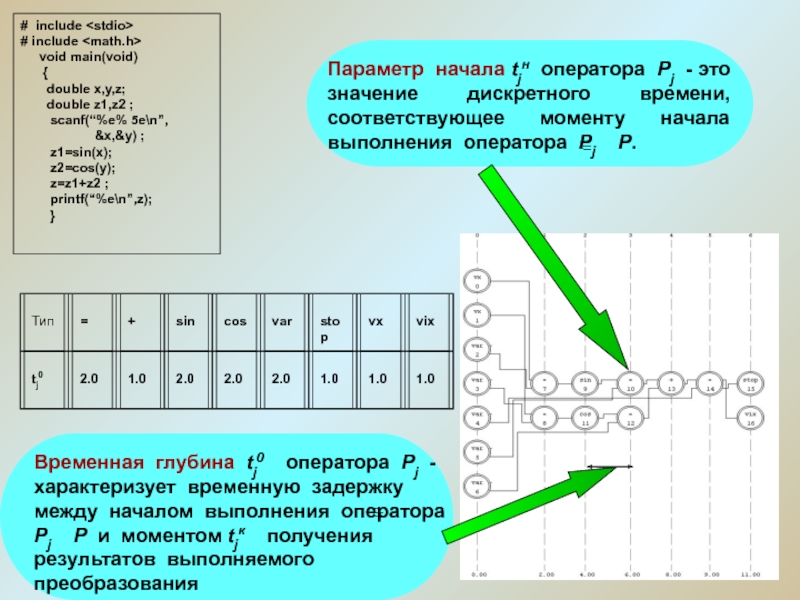
Параметр начала tjн оператора Рj - это значение дискретного времени, соответствующее моменту начала выполнения оператора Рj Р.
Временная глубина tj0 оператора Рj - характеризует временную задержку между началом выполнения оператора Рj Р и моментом tjк получения результатов выполняемого преобразования
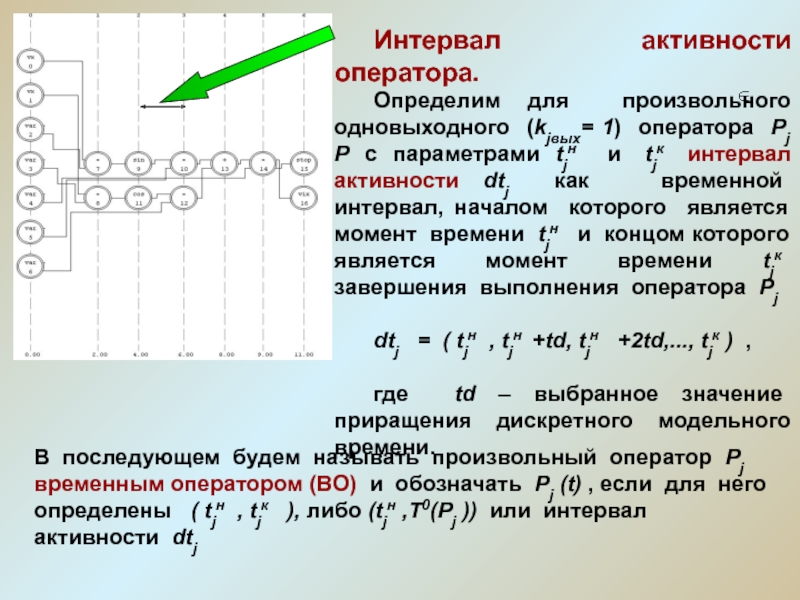
Слайд 13Интервал активности оператора.
Определим для произвольного одновыходного (kjвых= 1) оператора
Рj Р с параметрами tjн и tjк
интервал активности dtj как временной интервал, началом которого является момент времени tjн и концом которого является момент времени tjк завершения выполнения оператора Рj
dtj = ( tjн , tjн +td, tjн +2td,..., tjк ) ,
где td – выбранное значение приращения дискретного модельного времени.
В последующем будем называть произвольный оператор Рj временным оператором (ВО) и обозначать Рj (t) , если для него определены ( tjн , tjк ), либо (tjн ,T0(Рj )) или интервал активности dtj
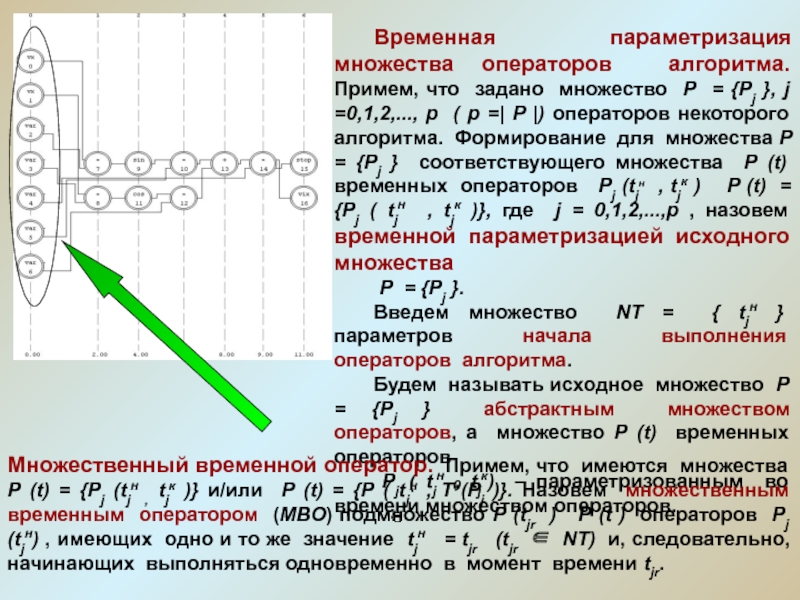
Слайд 14Временная параметризация множества операторов алгоритма. Примем, что задано множество Р
= {Pj }, j =0,1,2,..., р ( р =| P
|) операторов некоторого алгоритма. Формирование для множества Р = {Pj } соответствующего множества Р (t) временных операторов Pj (tjн , tjк ) Р (t) = {Pj ( tjн , tjк )}, где j = 0,1,2,...,p , назовем временной параметризацией исходного множества
Р = {Pj }.
Введем множество NT = { tjн } параметров начала выполнения операторов алгоритма.
Будем называть исходное множество Р = {Pj } абстрактным множеством операторов, а множество Р (t) временных операторов
Pj ( tjн , tjк) – параметризованным во времени множеством операторов.
Множественный временной оператор. Примем, что имеются множества Р (t) = {Рj (tjн , tjк )} и/или Р (t) = {Р ( tjн , T0(Рj )}. Назовем множественным временным оператором (МВО) подмножество Р (tjr ) Р (t ) операторов Рj (tjн) , имеющих одно и то же значение tjн = tjr (tjr NT) и, следовательно, начинающих выполняться одновременно в момент времени tjr.
Слайд 15 Определим параллельный алгоритм как временной алгоритм, в котором имеется
хотя бы одна пара операторов Рj (tjн , tjк )
и Рi (tiн, tiк ) c частично или полностью перекрывающимися интервалами активности dtj и dti , для которых выполняется условие dtj dti
Параллельный алгоритм
Определим последовательный алгоритм как временной алгоритм, имеющий единичное значение ширины h = 1.
Последовательный алгоритм
Слайд 17Второй вопрос. Временные Параллельные Граф-Схемы -
способ визуализации временных
параллельных
алгоритмов .
Временная параллельная граф-схема
Ранги временных операторов
Приоритеты временных операторов
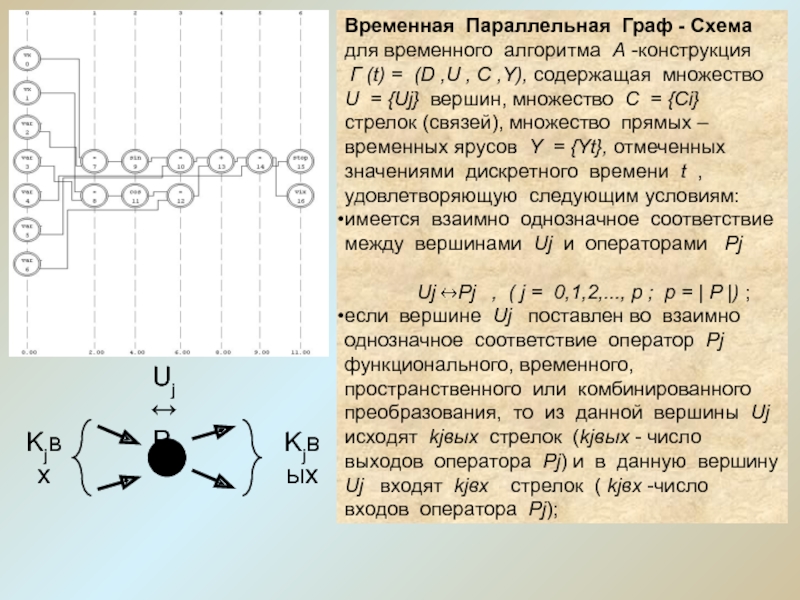
Слайд 18Временная Параллельная Граф - Схема для временного алгоритма А -конструкция
Г (t) = (D ,U , C ,Y), содержащая
множество U = {Uj} вершин, множество С = {Ci} стрелок (связей), множество прямых – временных ярусов Y = {Yt}, отмеченных значениями дискретного времени t , удовлетворяющую следующим условиям:
имеется взаимно однозначное соответствие между вершинами Uj и операторами Pj
Uj Pj , ( j = 0,1,2,..., p ; р = | P |) ;
если вершине Uj поставлен во взаимно однозначное соответствие оператор Рj функционального, временного, пространственного или комбинированного преобразования, то из данной вершины Uj исходят kjвых стрелок (kjвых - число выходов оператора Рj) и в данную вершину Uj входят kjвх стрелок ( kjвх -число входов оператора Рj);
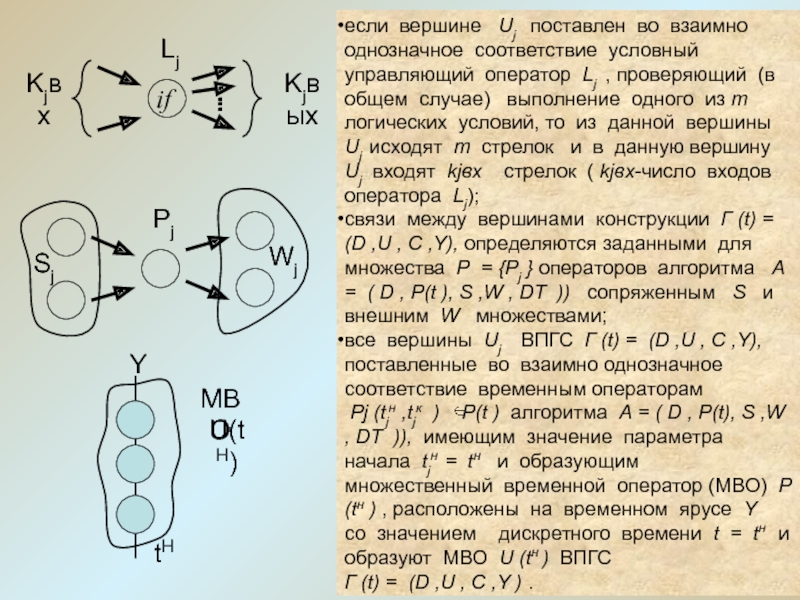
Слайд 19если вершине Uj поставлен во взаимно однозначное соответствие
условный управляющий оператор Lj , проверяющий (в общем случае)
выполнение одного из m логических условий, то из данной вершины Uj исходят m стрелок и в данную вершину Uj входят kjвх стрелок ( kjвх-число входов оператора Lj);
связи между вершинами конструкции Г (t) = (D ,U , C ,Y), определяются заданными для множества Р = {Pj } операторов алгоритма А = ( D , Р(t ), S ,W , DТ )) сопряженным S и внешним W множествами;
все вершины Uj ВПГС Г (t) = (D ,U , C ,Y), поставленные во взаимно однозначное соответствие временным операторам
Рj (tjн ,tjк ) Р(t ) алгоритма А = ( D , Р(t), S ,W , DТ )), имеющим значение параметра начала tjн = tн и образующим множественный временной оператор (МВО) Р (tн ) , расположены на временном ярусе Y со значением дискретного времени t = tн и образуют МВО U (tн ) ВПГС
Г (t) = (D ,U , C ,Y ) .
Слайд 20 Ранг временного оператора
Для произвольного временного оператора Рj ВПГС Г(t) понятие
ранга rj определяется следующим образом:
а) ранг rj = tj0 при Wj = (случай оператора Рj , являющегося выходным оператором алгоритма);
б) rj = max (rλ + tj0 ) ,если Wj (случай, когда оператор Рj представляет собой Pλ Wj внутренний оператор алгоритма, обеспечивающий формирование промежуточного результата, используемого другими, внешними по отношению к Рj , операторами Рλ алгоритма).
С содержательной точки зрения ранг rj оператора Рj задает максимальное значение времени от момента начала tjн выполнения оператора Рj до завершения решения задачи (то есть временную длину соответствующего маршрута в ВПГС Г (t)).
Слайд 21 Частный приоритет bj временного оператора Рj (в рамках
отдельного алгоритма) [1,2 ]:
а) bjδ = 1 при rj = max ri и ri < rj при i ≠ j ;
Pi Pδ
б) bjδ < biδ при rj = ri и tj0 < ti0 ;
в) bjδ < biδ при rj = ri , tj0 = ti0 и |Wj | > |Wi | ;
г) bjδ < biδ при rj = ri , tj0 = ti0 и |Wj | = |Wi | , но i < j .
Общие приоритеты dj операторов Рj различных алгоритмов будем определять следующим образом
dj = bjδ + max (biν), если jδ > min jν ,
ν Mδ Pi Pδ ν=1...κα
dj = bjδ , если jδ = min jν .
В последнем соотношении Мδ - множество номеров ν (ν 1...κ) алгоритмов, имеющих более высокие приоритеты baν по сравнению с приоритетом baδ рассматриваемого алгоритма, Рδ - множество операторов, относящихся к алгоритму с номером δ, имеющему приоритет f δ.
Слайд 22Си – программа циклического алгоритма
void main(void)
{
int s, r ;
int i, p, q, t, k ;
scanf ( “%d %d\n “, &s , &r ) ;
for (i=1; i<=20; i++)
{
s = s + 1 ;
r = (r + 1) % 2 ;
p = s * r ;
q = s + r ;
t = r – p ;
}
k = (t * q) / 10 ;
}
Таблица. Значения времени tj0 выполнения операторов (в тактах)
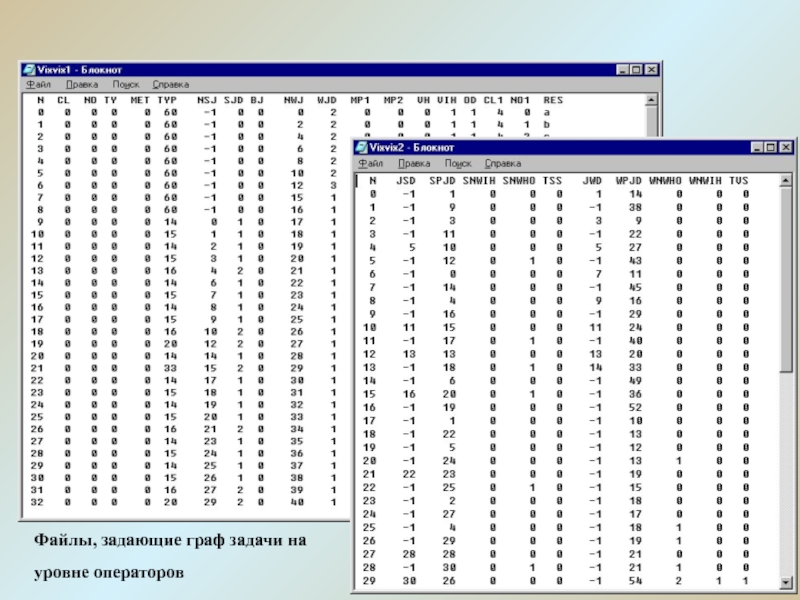
Слайд 23Файлы, задающие граф задачи на уровне операторов










![Лекция 11. Временные параллельные алгоритмы.
Тема 3. Методы Частный приоритет bj временного оператора Рj (в рамках отдельного алгоритма) Частный приоритет bj временного оператора Рj (в рамках отдельного алгоритма) [1,2 ]:](/img/thumbs/c9a378f2e13dc19921c446152a56aa62-800x.jpg)