Лекция

пустоту
Энтропия: термодинамическое и статистическое определения. Закон возрастания энтропии.
Энтропия идеального газа.

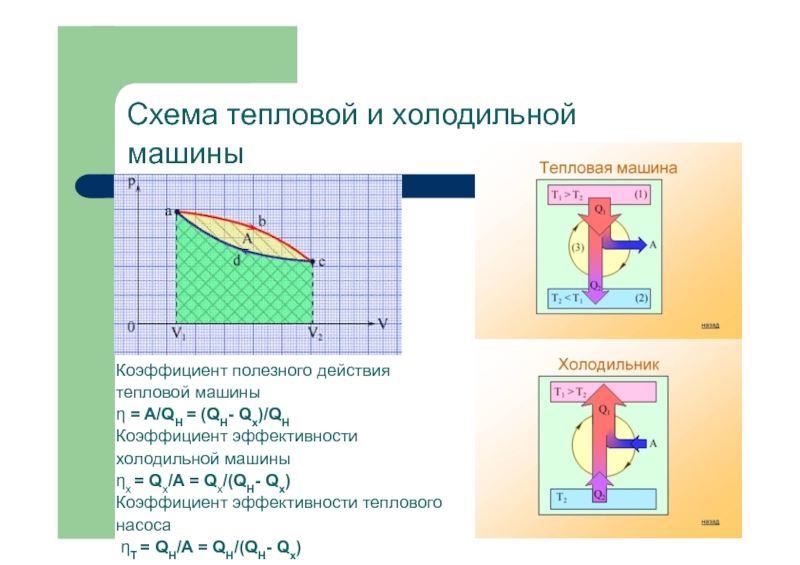
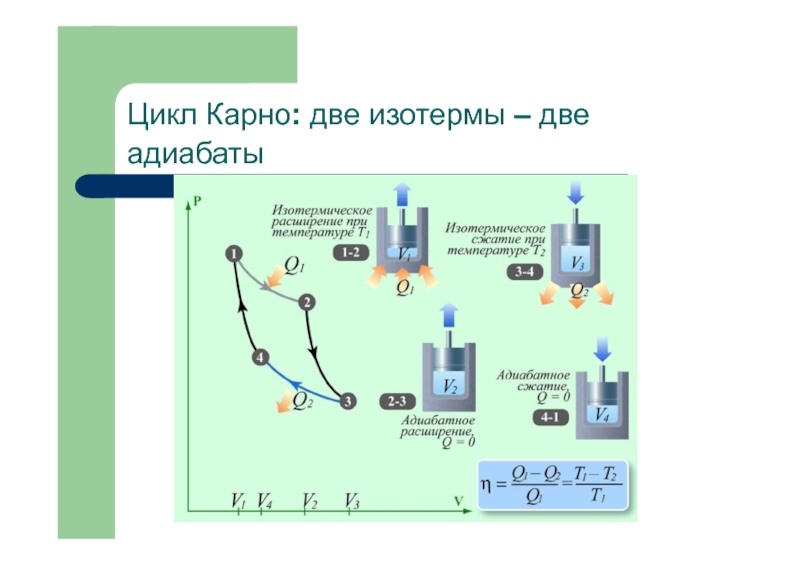
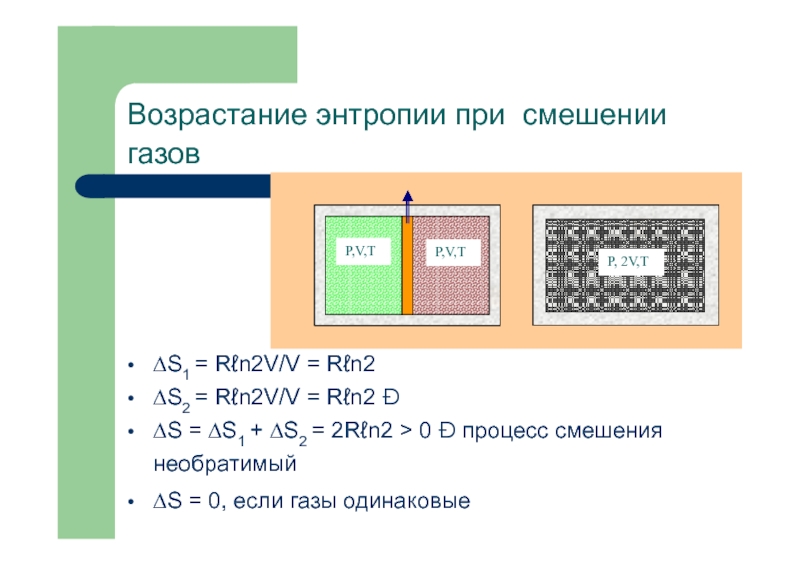
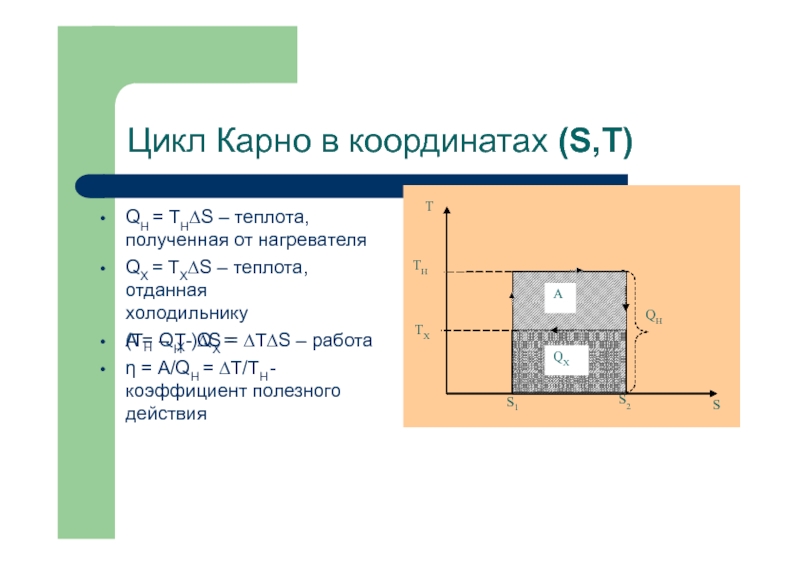
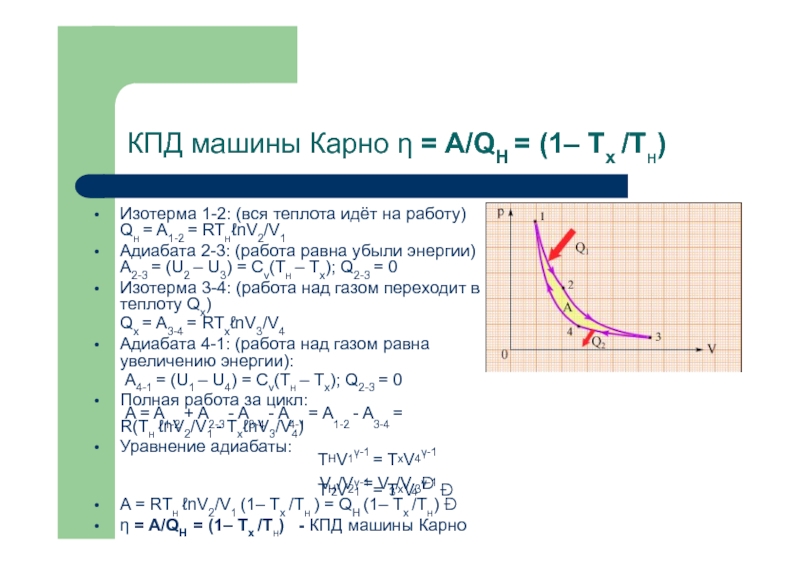
Возрастание энтропии при смешении газов.
Тепловые машины. Цикл Карно.

полностью превратить нельзя.
Теплообмен между горячим и холодным телом.
Расширение газа в

пустоту.
Диффузия – процесс необратимый: сахар в чае никогда не соберётся в кусок.

теплоты от тела холодного к телу горячему. (Р. Клаузиус, 1850

г.)
Невозможен круговой процесс, единственным результатом которого было бы производство работы за счёт охлаждения теплового резервуара (В. Томсон (лорд Кельвин), 1851 г.)
Невозможно построить периодически действующую машину, единственным результатом которой было бы поднятие груза за счёт охлаждения теплового резервуара (Планк)
Невозможен вечный двигатель второго рода (т.е. двигатель, работающий только за счёт охлаждения теплового резервуара).(В. Оствальд)

превратив тепло, полученное от одного теплового резервуара в работу. Тело

падает и нагревает более горячее тело: получили невозможный процесс Клаузиуса.

A/QH = (QH- Qx)/QH
Коэффициент эффективности холодильной машины
ηх = Qх/A =

Qх/(QH- Qx)
Коэффициент эффективности теплового насоса
ηT = QH/A = QH/(QH- Qx)

механическую работу
Циклически действующую тепловую машину можно создать только за счёт

неравновесной системы тел (второе начало термодинамики)
Максимальную работу даёт обратимая машина. В обратимой машине:
нет теплообмена между горячим и холодным телом
нет процессов расширения в пустоту
Машина Карно:
нагреватель с TH
холодильник TX
рабочее тело.
Единственный обратимый процесс для машины Карно – цикл Карно: две изотермы + две адиабаты
В таком цикле энтропия системы не изменяется:
∆S = ∆SH + ∆SX = 0

из одного состояния в другое равна приведённому количеству теплоты:
dS =

δQ/T; ∆S = ∫δQ/T
При любых процессах, протекающих в термодинамических изолированных системах, энтропия либо остаётся неизменной, либо возрастает: ∆S ≥ 0.
В состоянии равновесия энтропия замкнутой системы достигает максимума и никакие макроскопические процессы в такой системе невозможны.

CvdT/T + P/TdV
= CvdT/T + R/VdV Ð
S = S(V,T) =

CVℓnT + RℓnV + const
S = S(P,T) = CPℓnT - RℓnP + const
S = S(P,V) = CVℓnP + CPℓnV + const

= Rℓn2V/V = Rℓn2 Ð
∆S = ∆S1 + ∆S2 =

2Rℓn2 > 0 Ð процесс смешения необратимый
∆S = 0, если газы одинаковые

от нагревателя
QХ = TХ∆S – теплота, отданная холодильнику
A = QH -

QХ =

H Х

(T – T )∆S = ∆T∆S – работа

η = A/QH = ∆T/TH - коэффициент полезного действия

Q

Х

A

Q

Х

A

S

T

TН

TХ

S

1

S2

QХ

A

QН

при любом реальном процессе либо возрастает, либо остаётся неизменной, т.е.

изменение энтропии dS
≥ 0; знак равенства имеет место для обратимых процессов.
В состоянии равновесия энтропия замкнутой системы достигает максимума и никакие макроскопические процессы в такой системе невозможны.

– число способов, котором может быть реализовано данное макроскопическое состояние

системы (статистический вес или термодинамическая вероятность состояния системы).
Закон возрастания энтропии – соответствует переходу системы в более вероятное состояние. Максимально вероятным является состояние равновесия.

1-2: (вся теплота идёт на работу) Qн = A1-2 =

RTнℓnV2/V1
Адиабата 2-3: (работа равна убыли энергии) A2-3 = (U2 – U3) = Cv(Tн – Tx); Q2-3 = 0
Изотерма 3-4: (работа над газом переходит в теплоту Qx)
Qx = A3-4 = RTxℓnV3/V4
Адиабата 4-1: (работа над газом равна увеличению энергии):
A4-1 = (U1 – U4) = Cv(Tн – Tx); Q2-3 = 0
Полная работа за цикл:

A = A1-2 + A2-3 - A3-4 - A4-1 = A1-2 - A3-4 =

R(Tн ℓnV2/V1 - TxℓnV3/V4)
Уравнение адиабаты:

THV1γ-1 = TxV4γ-1 THV2γ-1 = TxV3γ-1 Ð

V2/V1 = V3/V4 Ð
A = RTн ℓnV2/V1 (1– Tx /Tн ) = QH (1– Tx /Tн) Ð
η = A/QH = (1– Tx /Tн) - КПД машины Карно

между двумя термостатами, равны, независимо от устройства машины и от

рода рабочего тела: ηкарно = (Tн – Tx)/Tн

Доказательство: «плохую» машину Карно запускаем по холодильному циклу, используя работу «хорошей» машины. Например, «плохая» машина забирает от холодильника 5 Дж, 5 Дж работы берёт от
«хорошей» машины и 10 Дж отдаёт нагревателю. «Хорошая» машина от нагревателя берёт 9 Дж и холодильнику возвращает 4 Дж.
Результат – невозможный процесс Клаузиуса.

не может превышать КПД машины Карно с теми же тепловыми

резервуарами.
Доказательство:
запустим машину Карно по холодильному циклу и при этом она, например, забирает от холодильника 5 Дж и отдаёт нагревателю 10 Дж, используя 5 Дж работы от
«хорошей» необратимой машины, которая забирает от нагревателя 9 Дж, а холодильнику возвращает 4 Дж. Результат – невозможный процесс Клаузиуса.